1: Concepto general- 2da ley de Newton
- Page ID
- 88495
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El viento que sopla sobre su casa, la Corriente del Golfo que fluye a través del Océano Atlántico Norte de Florida a Europa, la corriente en chorro a 10 km de altitud... Todos estos diferentes flujos en la atmósfera y en el océano se pueden entender utilizando ideas de la física de los fluidos.
Un fluido es cualquier sustancia que es capaz de fluir que puede ser un gas, un líquido, o en algunos casos incluso un sólido. En realidad, los fluidos consisten en moléculas, partículas que interactúan entre sí. Sin embargo, la mecánica de fluidos se ocupa de colecciones muy grandes de tales partículas y sería imposible describir todas las interacciones entre ellas. Por lo tanto, no se toman en cuenta las partículas individuales y sus interacciones: los fluidos se consideran como un continuo. Esencialmente, la mecánica de fluidos es la aplicación de la segunda ley de movimiento de Newton a un continuo que fluye. La segunda ley de Newton establece sucintamente:
\[F =m \dfrac{dv}{dt} \label{1.1}\]
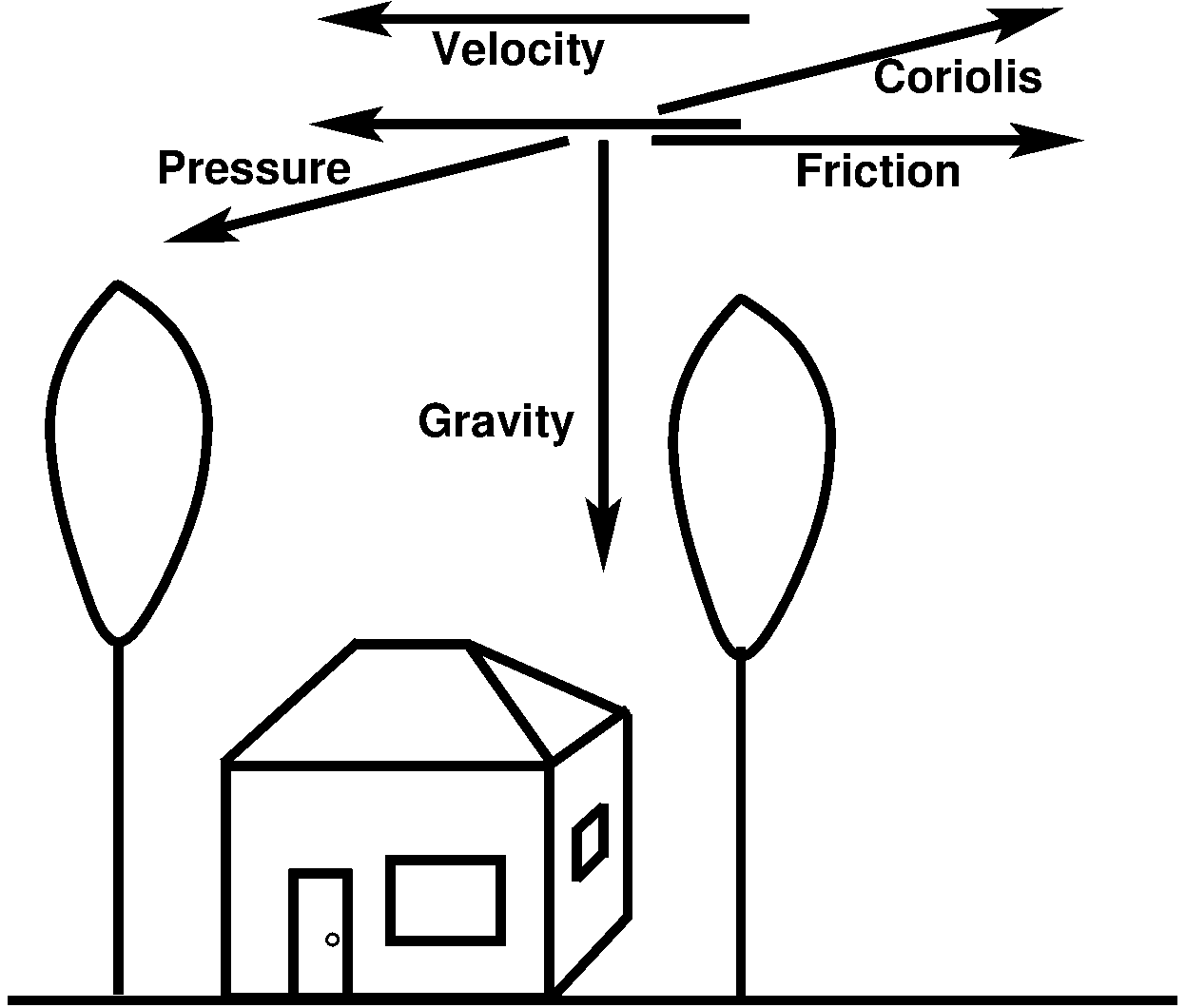
O bien, la tasa temporal de cambio en la velocidad (\(v\)) de un cuerpo es proporcional a la fuerza neta (\(F\)) aplicada a ese cuerpo. En consecuencia, el cambio en la velocidad de una pequeña parcela (infinitesimal) de fluido viene dada por la suma de todas las fuerzas que operan sobre esta parcela fluida. La imagen en la parte superior de esta página muestra el ejemplo de viento soplante, pero los mismos principios se aplican a los flujos oceánicos. Todo el tiempo, diversas fuerzas actúan sobre el flujo; cómo se desarrollará el flujo, depende de todas las fuerzas tomadas en conjunto. Para los flujos en la atmósfera y el océano, la colección de fuerzas se reduce a:
- Aceleración = fuerza de gradiente de presión + Fuerza Coriolis + fricción (horizontal)
- Aceleración = fuerza de gradiente de presión + gravedad + fricción (vertical)
O en términos matemáticos:
\[\dfrac{du}{dt}=-\dfrac{\left(\dfrac{dp}{dx}\right)}{\rho}+f * v +K_h \left(\dfrac{d^2u}{dx^2}+\dfrac{d^2u}{dy^2}\right)+K_v\dfrac{d^2u}{dz^2} \label{1.2a}\]
\[\dfrac{dv}{dt}=-\dfrac{\left(\dfrac{dp}{dy}\right)}{\rho}-f * u +K_h \left(\dfrac{d^2v}{dx^2}+\dfrac{d^2v}{dy^2}\right)+K_v\dfrac{d^2v}{dz^2} \label{1.2b}\]
\[\dfrac{dw}{dt}=-\dfrac{\left(\dfrac{dp}{dz}\right)}{\rho}-g+K_h \left(\dfrac{d^2w}{dx^2}+\dfrac{d^2w}{dy^2}\right)+K_v\dfrac{d^2w}{dz^2} \label{1.2c}\]
Aquí,\(u\) es la velocidad en la dirección zonal (Oeste a Este),\(v\) es la velocidad en la dirección meridional (Sur a Norte), y\(w\) es la velocidad en la dirección vertical. Además,\(p\) es la presión,\(\rho\) es la densidad del fluido,\(f\) el parámetro Coriolis, y\(g\) es la aceleración gravitacional. \(K_h\)y\(K_v\) son los coeficientes de fricción horizontal y vertical; estos son diferentes, porque en las grandes escalas atmosféricas y oceánicas, la dispersión del momento se debe principalmente a la turbulencia, más que a la difusión molecular. En las siguientes secciones, cada una de estas diferentes fuerzas se discutirá con más detalle.