2.5: ¿Y si eliges las variables equivocadas?

Incluir una variable irrelevante

¿Cuáles serían las consecuencias de incluir una variable irrelevante en el análisis de la estructura dimensional de un problema como el de fluir más allá de una esfera? Supongamos, contrario a los hechos pero sólo por el bien de la discusión, que la viscosidad no es importante para determinar$F_{D}$. Entonces la relación funcional para$F_{D}$ sería

$$F_{D}=f(U, D, \rho) \label{contrary}$$

Como antes, puede comenzar a hacer esta ecuación adimensional formando la misma fuerza de arrastre adimensional$F_{D} / \rho U^{2} D^{2}$ en el lado izquierdo. Pero ¿qué tal el lado derecho? Las tres variables$U$,$D$, y$\rho$ no se pueden combinar para formar una variable adimensional, porque no hay suficiente libertad para ajustar exponentes para hacer un producto$U^{a} D^{b} \rho^{c}$ adimensional; esto debe quedar claro a partir del procedimiento formal descrito anteriormente para su obtención$\rho U D / \mu$. Entonces, ¿qué toma el lugar del número de Reynolds del lado derecho? La respuesta es que el lado derecho debe ser una constante numérica: no existe una variable adimensional independiente. Entonces, si no$\mu$ fueran importantes en el flujo pasado una esfera, la fuerza adimensional$F_{D} / \rho U^{2} D^{2}$ sería una constante más que una función del número de Reynolds. Generalizar: si se elimina una variable original del problema, también se debe eliminar una variable adimensional. En una gráfica de$C_{D}$ vs.$\mathrm{Re}$ los puntos experimentales caerían a lo largo de una línea recta paralela al$\mathrm{Re}$ eje, como se muestra esquemáticamente en la Figura$\PageIndex{1}$. Ahora mira hacia atrás en la gráfica real de$C_{D}$ vs$\mathrm{Re}$ en la Figura 2.3.1. En un amplio rango de números de Reynolds de aproximadamente$10^{2}$ a mayor que$10^{5}$,$C_{D}$ es casi independiente del número de Reynolds. Porque$\mu$ es la única variable que aparece en el número de Reynolds pero no en$C_{D}$, esto te dice que de hecho no$\mu$ es importante para determinar$F_{D}$ en general$\mathrm{Re}$. Las razones de esto se discuten en el Capítulo 3.

Figura$\PageIndex{1}$: Cómo sería la gráfica de la fuerza de arrastre adimensional frente al número de Reynolds para el flujo alrededor de una esfera si la viscosidad no fuera importante.

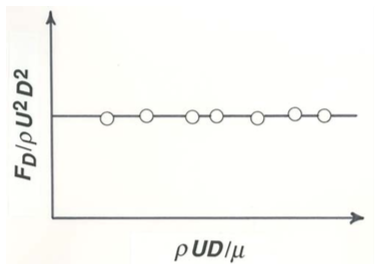
Ahora puedes ver por qué hay alguna ventaja práctica al usar$F_{D} / \rho U^{2} D^{2}$ como variable adimensional dependiente. Los otros tres mencionados anteriormente contienen$\mu$, y así en una gráfica de cualquiera de ellos contra$\rho U D / \mu$ el segmento de la curva para el cual no$\mu$ es importante se trazaría como una línea inclinada más que como una línea horizontal, y la falta de importancia de no$\mu$ sería tan fácil de reconocer.

Figura$\PageIndex{2}$: Cómo sería la gráfica de la fuerza de arrastre adimensional frente al número de Reynolds para el flujo alrededor de una esfera remolcada cerca de una pared sólida en un cuerpo de agua inmóvil si la distancia de la esfera desde la pared no se mantiene constante de un juicio a otro.

Omitir una variable relevante

También se deben considerar las consecuencias de omitir de consideración una variable importante. Por ejemplo, si no hubieras tenido cuidado de mantener la esfera bien alejada de la pared del vaso que contiene el fluido, encontrarías (Figura$\PageIndex{2}$) que los puntos experimentales se trazan en una banda dispersa alrededor de la curva de$C_{D}$ vs.$\mathrm{Re}$ en la Figura 2.3.1. Esto te dice que alguna otra variable es importante para determinar$F_{D}$ y que inadvertidamente la has dejado variar, asumiendo, por supuesto, que tus mediciones están libres de errores en primer lugar. El culpable obvio es$y$, la distancia del centro de la esfera desde la pared (Figura$\PageIndex{3}$), porque la proximidad de la esfera a la pared sólida distorsiona el patrón de flujo alrededor de la esfera y así cambia las fuerzas de fluido sobre la esfera en cierta medida. Con$y$ incluido en el análisis, la relación funcional para$F_{D}$ es de la forma

$$F_{D}=f(U, D, \rho, \mu, y) \label{2.7}$$

Figura$\PageIndex{3}$: Remolcar una esfera paralela a una pared plana sólida cercana.

En la ecuación no dimensionalizadora\ ref {2.7} deberías esperar de nuevo tener una fuerza de arrastre adimensional a la izquierda y el número de Reynolds a la derecha. Pero, ¿qué pasa con la nueva variable$y$? Se puede utilizar para formar una variable adimensional independiente más, de la misma manera que formó el número de Reynolds. Tiene que haber al menos otra variable, porque$y$ tiene que aparecer en algún lugar del lado derecho de la versión no dimensionalizada de la Ecuación\ ref {2.7}. Una elección natural para esta nueva variable es$y/D$ (o$D/y$). En cambio podrías formar otro número de Reynolds,$\rho U y / \mu$. Pero solo dos de las tres variables$\rho U D / \mu$,$\rho U y / \mu$, y$y / D$ son independientes entre sí: la adición de una nueva variable independiente al problema agrega solo una nueva variable adimensional independiente. También vale la pena señalar que se puede llegar al segundo número de Reynolds,$\rho U y / \mu$, multiplicando el primero,$\rho U D / \mu$, por la nueva variable adimensional$y / D$. Esto es una ilustración del principio de que siempre se puede sustituir una variable adimensional en un conjunto de variables adimensionales por otra formada multiplicándola o dividiéndola por una de las otras, o con algún poder o raíz de una de las otras. Así que en forma adimensional Ecuación\ ref {2.7} es entonces

$$\frac{F_{D}}{\rho U^{2} D^{2}}=f\left(\frac{\rho U D}{\mu}, \frac{y}{D}\right) \label{2.8}$$

La función en la Ecuación\ ref {2.8} se trazaría como una superficie curva en una gráfica tridimensional con$C_{D}$$\mathrm{Re}$, y$y/D$ a lo largo de los ejes (Figura$\PageIndex{4}$). Los dos planos perpendiculares al$y/D$ eje de la Figura$\PageIndex{4}$ muestran el rango sobre el cual$y/D$ varió en tus experimentos sin que te des cuenta de que es importante. La proyección del segmento de la superficie entre estos dos planos sobre el$\mathrm{Re}$ plano$C_{D}$ — es la banda en la que caerían tus puntos experimentales. La intersección de la superficie con el plano$y/D = 0$, también mostrada en la proyección, representa la curva que habrías obtenido si siempre hubieras mantenido la esfera muy alejada de la pared; es la misma que la curva de la Figura 2.3.1.

Figura$\PageIndex{4}$: Para el remolque de una esfera paralela a una pared plana sólida cercana, los datos de un gran número de ensayos se representarían como una superficie en una gráfica tridimensional del coeficiente de arrastre, el número de Reynolds y la relación de distancia entre el diámetro de la pared y la esfera. La gráfica en la parte superior derecha muestra, en una gráfica de coeficiente de arrastre vs número de Reynolds, dos curvas correspondientes a dos valores diferentes de la relación de distancia de diámetro de pared a esfera. Estas curvas son las intersecciones de toda la superficie con planos paralelos al$\mathrm{Re}$ plano$C_{D}$ —.

Involucrar gravedad

Se podría llevar el análisis un paso más allá moviendo la esfera horizontalmente justo debajo de la superficie libre de un líquido en reposo en un campo gravitacional (Figura$\PageIndex{5}$). De importancia ahora no solo es la distancia y de la esfera por debajo de la superficie libre sino también la aceleración de la gravedad$g$: si el movimiento de la esfera distorsiona la superficie libre, las fuerzas de gravedad desequilibradas tenderían a aplanar la superficie nuevamente, y se pueden generar ondas gravitacionales superficiales. Entonces

$$F_{D}=f(U, D, \rho, \mu, y, g) \label{2.9}$$

Figura$\PageIndex{5}$: Remolcar una esfera horizontalmente a través de un líquido inmóvil, no muy por debajo de la superficie libre del líquido.

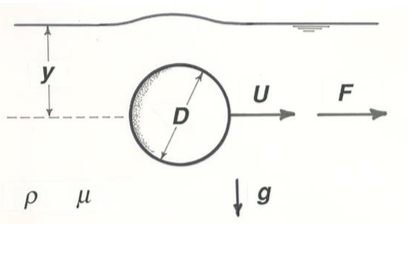
Esto agrega otra variable adimensional independiente, y esa variable debe incluir$g$. Hay cinco posibilidades:$\mu g / \rho U^{3}$,$\rho^{2} g D^{3} / \mu^{2}$,$\rho^{2} g y^{3} / \mu^{2}$, y$U^{2} / g D$$U^{2} / g y$, más variantes obvias obtenidas por inversión y exponenciación. (Podría intentar construir estos combinando$U$,,$\rho$,$\mu$$D$, y$y$ tres a la vez con$g$ y pasando por el procedimiento descrito anteriormente para$\mathrm{Re}$. También volverías a entrar$y/D$ en el proceso.) Cualquiera de estos cinco bastaría para expresar el efecto de$g$ sobre la fuerza de arrastre. Nuevamente solo uno es independiente, porque todos los demás se pueden obtener combinando ese (lo que elija) con cualquiera$\rho U D / \mu$ o$y/D$. Sería convencional, en un problema como este, usar$U /(g y)^{1 / 2}$ como la variable independiente agregada. La forma adimensional de la Ecuación\ ref {2.9} es entonces

$$\frac{F D}{\rho U^{2} D^{2}}=f\left(\frac{\rho U D}{\mu}, \frac{U^{2}}{g y}, \frac{y}{D}\right) \label{2.10}$$

La raíz cuadrada de una variable como$U^{2} / g y$ o$U^{2} / g D$, con una velocidad, una variable de longitud, y$g$, se llama un número de Froude, generalmente denotado por$\mathrm{Fr}$. Es natural, aunque no esencial, usar$U^{2} / g y$ aquí porque entonces cada una de las cuatro variables adimensionales en la relación funcional puede ser vista como formada combinando$F_{D}$,,$\mu$$y$, y$g$ a su vez con las tres variables$\rho$,$U$, y $D$; véase el siguiente párrafo para más detalles.

Nota

La función en la Ecuación\ ref {2.10} se trazaría como una “superficie” de cuatro dimensiones en una gráfica de$C_{D}$ vs.$\mathrm{Re}$,$\mathrm{Fr}$, y$y/D$. Es difícil visualizar tal gráfica. Un buen sustituto sería trazar una gráfica tridimensional para cada una de una serie de valores de una de las variables adimensionales independientes. El problema es que hay un número infinito de estas gráficas tridimensionales. (Recuerdo que una vez leí en alguna parte que para expresar gráficamente la relación entre dos variables se necesita una página, y para expresar la relación entre tres variables se necesita un libro de páginas, y para expresar la relación entre cuatro variables se necesita una biblioteca de libros. ¡Para cinco variables necesitarías un mundo de bibliotecas!

Manejo de múltiples variables

Supongamos que se había dado cuenta al principio de que las siete variables de la Ecuación\ ref {2.9} son importantes en el problema. La forma sistemática de obtener cuatro variables adimensionales a la vez es solo una extensión del método descrito en una sección anterior para obtener el número de Reynolds. Formar cuatro productos eligiendo tres de las siete variables (las variables “repetitivas”) para que sean las elevadas a los exponentes$a$$b$,$c$ y usando cada una de las cuatro variables restantes a su vez como la que se eleva al exponente$1$ (o a cualquier otro exponente fijo, para eso importa). Puedes verificar por ti mismo que si eliges$\rho$,$U$, y$D$ como las tres variables repetitivas, los cuatro productos$\rho^{a} U^{b} D^{c} F_{D}$,,$\rho^{a} U^{b} D^{c} \mu$$\rho^{a} U^{b} D^{c} y$, y$\rho^{a} U^{b} D^{c} g$ producirían las cuatro variables adimensionales en la Ecuación\ ref {2.10}, excepto que$U^{2} / g D$ aparece en lugar de $U^{2} / g y$. Resulta que para que este procedimiento funcione, las limitaciones en la elección de las tres variables repetitivas son que (1) entre ellas incluyen las tres dimensiones$\mathrm{M}$,,$\mathrm{L}$$\mathrm{T}$, y (2) sean dimensionalmente independientes entre sí, en el sentido de que no se puede obtener el dimensiones de cualquiera multiplicando las dimensiones de las otras dos después de elevarlas a algunos exponentes. Estas restricciones solo aseguran que obtenga conjuntos solucionables de ecuaciones simultáneas.