3.2: Clases y Proposiciones Categóricas

Para Aristóteles, la unidad lógica fundamental es la clase. Las clases son solo conjuntos de cosas, conjuntos que podemos elegir usando el lenguaje. La forma más sencilla de identificar una clase es usando un sustantivo plural: árboles, nubes, asteroides, personas, todas estas son clases. Los nombres para las clases también pueden ser gramaticalmente más complejos. Podemos modificar el sustantivo plural con un adjetivo: 'gente rica' escoge una clase. (¿Ves lo que hice ahí?) Las frases preposicionales pueden especificar aún más: 'gente rica de Italia' elige una clase diferente. Las modificaciones pueden continuar indefinidamente: 'gente rica de Italia que hizo fortuna en el sector inmobiliario y cuyas abuelas se rumoreaba que eran amantes secretas de Benito Mussolini' elige otra clase más, que es o muy pequeña, o posiblemente vacía, no lo sé. (Las clases vacías son solo clases sin miembros; luego hablaremos más sobre ellas).

Nos referiremos a los nombres de las clases como 'class-terms', o simplemente 'términos' para abreviar. Dado que para Aristóteles la unidad lógica fundamental es la clase, y dado que los términos son los bits del lenguaje que eligen clases, la lógica de Aristóteles a menudo se denomina “lógica de término”. Esto contrasta con la lógica que estudiaremos en el próximo capítulo, Lógica sentencial, llamada porque toma la unidad lógica fundamental para ser la proposición, y las oraciones son el vehículo lingüístico para elegirlas.

Por supuesto, la Lógica Aristotélica también debe tratar con proposiciones —aquí estamos evaluando argumentos, y por definición esos son solo conjuntos de proposiciones— pero como las clases son la unidad lógica fundamental, Aristóteles se restringe a un tipo particular de proposición: las proposiciones categóricas. 'Categoría' no es más que un sinónimo de 'clase'. Las proposiciones categóricas son proposiciones que hacen un reclamo sobre la relación entre dos clases. Este es el primer paso para domar el lenguaje natural: la Lógica Aristotélica sólo evaluará argumentos conformados íntegramente por proposiciones categóricas. Nos estamos limitando a una porción restringida del lenguaje, frases que expresan este tipo de proposiciones, que contarán con dos términos de clase, términos que eligen las clases cuya relación se describe en la proposición categórica. Pronto, pondremos más restricciones a las formas que pueden tomar estas oraciones, pero por ahora discutiremos proposiciones categóricas en general.

Nuevamente, las proposiciones categóricas hacen una aseveración sobre la relación entre dos clases. Aquí hay tres posibilidades:

(1) Inclusión completa: una clase está contenida enteramente dentro de la otra.
Ejemplo: Clase 1 = personas; Clase 2 = bípedos. La primera clase está contenida enteramente en la segunda; cada persona es bípedo. (Incluso amputados. Ser bípedo es pertenecer a una especie que naturalmente tiene dos patas.)

(2) Inclusión parcial: una clase está parcialmente contenida dentro de la otra; las dos clases tienen al menos un miembro en común.

Ejemplo: Clase 1 = personas; Clase 2 = nadadores. Algunas personas nadan; otras no. Algunos nadadores son personas; algunos no lo son (peces, por ejemplo). Estas dos clases se superponen, pero no del todo.

(3) Exclusión: las dos clases no tienen ningún miembro en común; son exclusivas. Ejemplo: Clase 1 = personas; Clase 2 = aves. Ninguna gente es aves; ninguna ave es gente. A pesar de Batman (el tío no es realmente un murciélago; además, los murciélagos no son pájaros; los petirrojos son, pero de nuevo, Robin no es en realidad un pájaro, solo un tipo que se viste como uno).

Dadas estas consideraciones, podemos (más o menos) definir formalmente proposiciones categóricas:

Una proposición categórica es una afirmación sobre la relación entre dos clases —llamarlas S y P— que o bien afirma o niega que S esté total o parcialmente incluida en P. (Nótese que negar que S esté incluso parcialmente incluida en P es lo mismo que afirmar que S y P son exclusivos).

Aristóteles señaló que, dada esta definición, existen cuatro tipos de proposición categórica. Los discutiremos a su vez.

Los cuatro tipos de proposición categórica

Afirmativo universal (A) (Dado que 'Afirmativo universal' —junto con los nombres de los otros tres tipos de proposición categórica— es un poco bocado, seguiremos la costumbre y asignaremos las cuatro categorías (abreviación de 'proposiciones categóricas') apodos de una sola letra. Lo afirmativo universal es la proposición A.)

Este tipo de proposición afirma toda la inclusión de la clase S en la clase P —dice que cada miembro de S también es miembro de P. La expresión canónica de esta proposición es una frase de la forma 'Todas las S son P'.

Vale la pena señalar en este punto por qué elegimos 'S' y 'P' como símbolos para términos genéricos de clase. Eso es porque el primero es el sujeto gramatical (S) de la oración, y el segundo es el predicado gramatical (P). Este patrón se mantendrá para los otros tres tipos de proposición categórica.

De vuelta a lo afirmativo universal, Una proposición. Afirma la inclusión completa. Por ejemplo, la frase 'Todos los hombres son mortales' expresa una proposición de este tipo, una que es cierta. 'Todos los hombres son canadienes' también expresa una proposición afirmativa universal, una que es falsa.

En aras de la concreción, escojamos clases de materia y predicado que podamos usar como ejemplos de referencia mientras hablamos de cada uno de los cuatro tipos de proposición categórica. Vamos a S = lógicos y P = tirones. La proposición A que presenta estas dos clases es expresada por 'Todos los logísticos son idiosas'. (Seguiremos siendo agnósticos sobre si es cierto o falso).

Cuando llegue el momento de probar argumentos de validez —el último paso en el proceso que acabamos de comenzar— será conveniente para nosotros representar los cuatro tipos de proposiciones categóricas pictóricamente. La forma básica de las imágenes serán dos círculos superpuestos, con el círculo de la izquierda representando la clase de sujeto y el círculo de la derecha representando la clase de predicado. Me gusta esto:

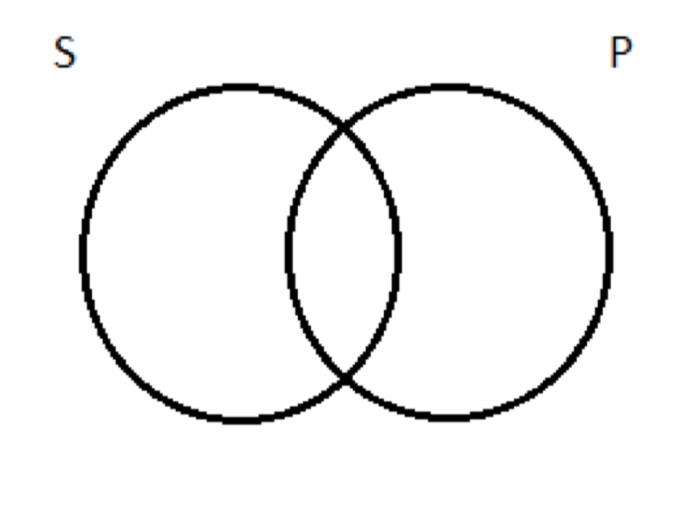
Para representar los cuatro tipos de proposiciones categóricas, modificaremos este diagrama básico de dos círculos sombreando partes de él o haciendo marcas dentro de los círculos.

Sin embargo, antes de llegar a la representación específica de la proposición A, hablemos de lo que hace el diagrama básico de dos círculos. Divide el universo en cuatro regiones, a las que podemos asignar números como este:

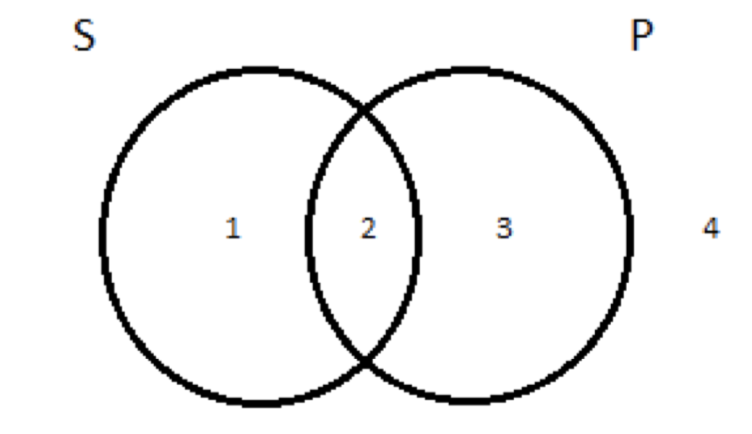
Hablemos de lo que hay dentro de cada una de las cuatro regiones si tomamos S para ser la clase de logísticos y P para ser la clase de idiotos.

La región 1 es la porción del círculo S que no se solapa con el círculo P. Estas son cosas en la clase de materia pero fuera de la clase de predicado; son logísticos que no son idioteces. Yo nunca lo conocí, pero no hay evidencia en el registro histórico que indique que Aristóteles era cualquier cosa menos un caballero. Entonces Aristóteles es uno de los habitantes de la región 1, un lógico que no es un imbécil.

La Región 2 es el área de superposición entre las clases de sujeto y predicado; sus residentes son miembros de ambas. Entonces aquí tenemos a los lógicos que también son imbéciles. Gottlob Frege, un lógico alemán del siglo XIX, es el innovador más importante en la historia de la lógica que no sea Aristóteles. Además, resulta que era un enorme imbécil. Era un gran antisemita. Entonces Frege vive en la región 2; es tanto lógico como imbécil.

La Región 3 es la porción del círculo P que no se superpone con S. Estos son miembros de la clase de predicados —idiotas, en nuestro ejemplo— que no son miembros de la clase de materia, no logísticos. Aquí es donde viven los imbéciles no lógicos. Donald Trump es residente de la región 3. El tipo es claramente un imbécil y con la misma claridad, no un lógico. (Llevo una década usando a Trump en este ejemplo; no voy a parar solo porque consiguió presidente electo. Además, entiendo que incluso los partidarios de Trump reconocerían que es un imbécil. Lo dice como es y no le importa qué sentimientos se lastiman, o algo así, ¿verdad?)

La región 4 es, todo lo demás. Son todas las cosas que están fuera tanto de las clases de sujeto como de predicado, cosas que no son ni ians de lógica ni idiotas. ¿Sabes quién parece simpático, pero no es un lógico? Beyoncé. Ella vive en la región 4. Pero así hacen muchas y muchas otras cosas: el planeta Júpiter no es ni lógico ni imbécil; está ahí con Beyoncé, también. Al igual que la llanta delantera izquierda del auto de mi esposa. Y el segundo ladrillo más pequeño de la Gran Muralla China. Y así sucesivamente.

Tanto para el diagrama de dos círculos en blanco y cómo talla el universo. Lo que queremos averiguar es cómo alterar ese diagrama para que terminemos con una imagen de la proposición afirmativa universal. Nuestro ejemplo particular de una proposición A es que todos los logísticos son imbéciles. ¿Cómo hacemos una imagen de eso, usando los dos círculos como nuestro punto de partida? Bueno, piénsalo de esta manera: cuando decimos que todos los lógicos son idiotas, lo que realmente estamos diciendo es que cierto tipo de cosas no existe; no existe tal cosa como un lógico no cecino. Es decir, a pesar de lo que dije anteriormente sobre Aristóteles, la región 1 está vacía, según esta proposición (que, de nuevo, puede o no ser cierta; no importa si es verdad o no; solo estamos tratando de averiguar cómo dibujar un cuadro que capte la afirmación que hace). Para representar el vacío, adoptaremos la convención de sombreado en la (s) región (es) relevante (s) del diagrama. Entonces nuestra imagen de lo afirmativo universal se ve así:

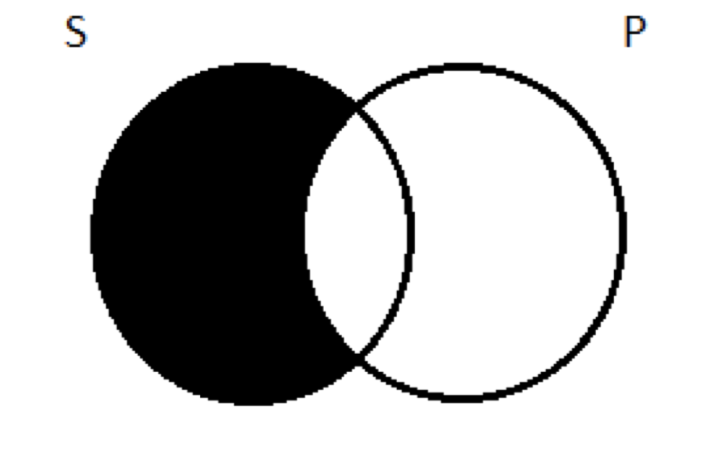
Todas las S son P significa que no encontrarás ningún miembro de S que esté fuera del círculo P (ni logísticos que no sean idioteces). El lugar en el diagrama donde podrían haber estado tales cosas se borra para indicar su vacío. La única porción de S que queda como espacio viable es dentro del círculo P, en lo que llamamos región 2 (los logísticos que sí encuentres serán todos idiotas).

Una pregunta razonable podría plantearse en este punto: ¿por qué dibujamos lo afirmativo universal de esa manera, en lugar de otra, alternativa y posiblemente más intuitiva? Una proposición afirma toda la inclusión, que S está completamente contenida dentro de P. No es la manera obvia de representar ese estado de cosas más así:

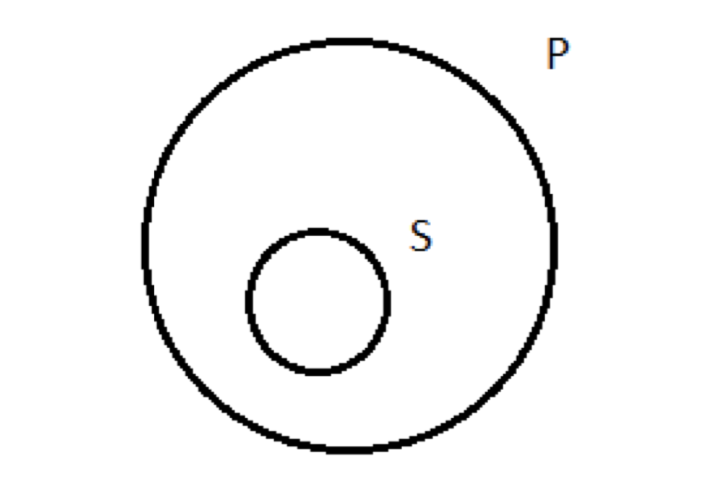
S completamente contenida dentro de P. Fácil. ¿Por qué molestarse con los círculos superpuestos y el sombreado?

No hay nada malo en esta representación alternativa de lo afirmativo universal; captura la afirmación que se está haciendo. Adoptamos la primera representación alternativa por razones puramente prácticas: cuando llegue el momento de probar argumentos de validez, vamos a usar estas imágenes; y nuestro método dependerá de que nuestros cuatro tipos de proposiciones categóricas sean representadas comenzando con el mismo diagrama básico de dos círculos superpuestos, con sombreado y marcas en el interior. Estos diagramas, como sabrán, se llaman “Diagramas de Venn”. Ellos llevan el nombre del lógico inglés del siglo XIX John Venn, quien los inventó específicamente como un medio más fácil de probar argumentos de validez en la lógica aristotélica (las cosas eran más difíciles de manejar antes de la innovación de Venn). Resulta que Venn'smethod solo funciona si comenzamos con los círculos superpuestos para los cuatro tipos de proposición categórica. Entonces eso es con lo que vamos.

Negativo universal (E)

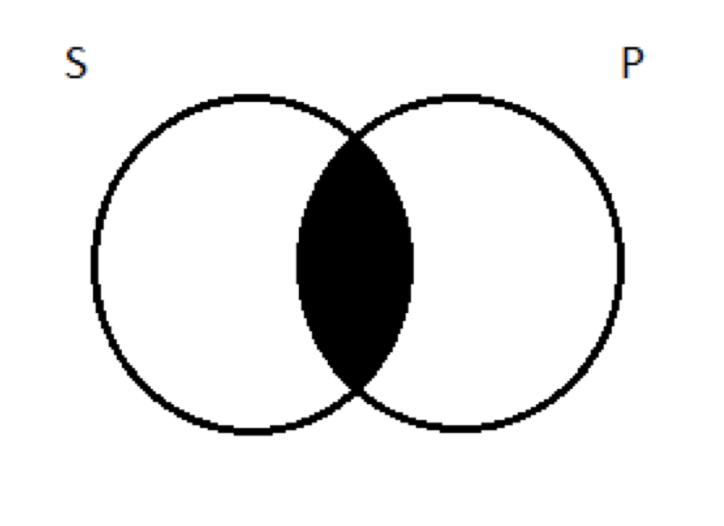
Este tipo de proposición niega que S esté incluso parcialmente incluido en P. Dicho de otra manera: afirma que S y P son exclusivas—que no tienen miembros en común. La expresión canónica de esta proposición es una frase de la forma 'No S are P'. Entonces, por ejemplo, la frase 'No hay perros son gatos' expresa una verdadera proposición negativa universal; la oración 'No hay animales son gatos' expresa una falsa.

Nuevamente, queremos pensar en cómo representar este tipo de proposición usando el diagrama estándar de Venn de dos círculos. Piensa en la proposición de que ningún lógico es imbécil. ¿Cómo hacemos un dibujo de esta afirmación? Bueno, como decíamos, las proposiciones E nos dicen que las dos clases no tienen ningún miembro en común. La región del diagrama de dos círculos donde hay miembros de ambas clases es el área de superposición en la imagen (lo que denominamos región 2 arriba). La proposición negativa universal nos dice que ahí no hay nada. Entonces, si afirmo que ningún lógico es imbécil, estoy diciendo que, contrariamente a mis afirmaciones anteriores sobre la sacudida de Gottlob Frege, no, no existe tal cosa como un gilipollas lógico. La región dos está vacía, y así la sombreamos:

Afirmativo particular (I)

Este tipo de proposición afirma que S está parcialmente incluida en P. Su expresión canónica es una oración de la forma 'Algunas S son P'. Entonces, por ejemplo, 'Algunos marineros son pirates' expresa una verdadera proposición afirmativa particular; 'Algunos luchadores de sumo son palomas 'expresa una falsa.

Antes de hablar sobre cómo representar las proposiciones I con un diagrama de Venn, necesitamos discutir la palabra 'algunos'. Recuerden, en la Lógica Aristotélica estamos domando el lenguaje natural restringiéndonos a una porción bien educada del mismo, frases que expresan proposiciones categóricas. Estamos proponiendo usar oraciones con la palabra 'algunos' en ellas. 'Algunos ', sin embargo, no se comporta particularmente bien, y vamos a tener que ponerlo en línea antes de continuar.

Considera esta afirmación: “Algunos votantes republicanos son dueños de armas”. Esto es cierto, y comunica al oyente el hecho de que hay cierta superposición entre las clases de votantes republicanos y los dueños de armas. Pero también comunica algo más, es decir, que algunos de esos republicanos no son dueños de armas. Esta es una implicación bastante típica (recordemos nuestra discusión sobre este fenómeno lingüístico en el Capítulo 2, cuando miramos la falacia de la equívoco): cuando decimos que algunos lo son, también comunicamos que algunos no lo son.

Pero hay momentos en los que usamos 'algunos' y no implicamos que algunos no lo son. Supongamos que estás hablando con tu mamá, y mencionas que estás leyendo un libro de lógica. Por alguna razón, tu mamá siempre ha sentido curiosidad por los libros de lógica, y te pregunta si son una buena lectura. (Solo juega aquí) Respondes: “Bueno, mamá, te puedo decir esto seguro: Algunos libros de lógica son aburridos. Deberías ver este libro que estoy leyendo ahora; ¡es un festival de snooze-fest total!” En este caso, dices que algunos libros de lógica son aburridos en base a tu experiencia con este libro en particular, pero no implicas que algunos libros de lógica no sean aburridos; por lo que sabes, todos los libros de lógica son aburridos, es simplemente imposible escribir un libro de lógica emocionante. Este es un uso perfectamente legítimo de la palabra 'algunos', donde todo lo que significa es que hay al menos uno: cuando pronuncias 'algunos libros de lógica son aburridos', todo lo que comunicas es que hay al menos un libro de lógica aburrido (este, el que estás leyendo).

Esto es un poco de ingobernabilidad del lenguaje natural con la que debemos lidiar: a veces cuando usamos la palabra 'algunos', implicamos que algunos no lo son; otras veces, no lo hacemos, solo comunicando que al menos uno es. Cuando usamos 'algunos' en la Lógica Aristotélica, necesitamos saber con precisión qué se dice. Entonces elegimos: 'algunos' significa 'hay al menos uno'. 'Algunas S son P' nos dice que esas dos clases tienen al menos un miembro en común, y nada más. 'Algunos marineros son piratas' significa que hay al menos un marinero que también es pirata, y eso es todo. No hay implicación de que algunos marineros no sean piratas; al menos uno de ellos lo es, y por lo que sabemos, todos lo son. (La justificación de esta elección requiere de un argumento, que no voy a hacer aquí. La idea básica es que el bit de 'algunos no son' que a menudo se comunica no forma parte del significado central de 'algunos'; es una implicación, que es algo que (a menudo, pero no siempre) se comunica por encima del significado central).

Esto puede confundir a la gente, así que vale la pena repetirlo. Diablos, vamos a sangrarlo:
'Algunos' significa 'hay al menos uno', y eso es todo. No implica que algunos no lo sean.

Con eso fuera del camino, podemos dirigir nuestra atención al diagrama de Venn para lo afirmativo particular. Hace la aseveración de que S y P tienen al menos un miembro en común. Volviendo a nuestro ejemplo concreto, la frase 'Algunos lógicos son imbécicos' hace la afirmación de que hay al menos un lógico que es un imbécil. (De hecho, esto es cierto: Gottlob Frege era un imbécil antisemita). ¿Cómo hacemos un dibujo de esto? Necesitamos indicar que hay al menos una cosa en el área de superposición entre los dos círculos del diagrama, al menos una cosa dentro de la región 2. Hacemos esto dibujando una X:

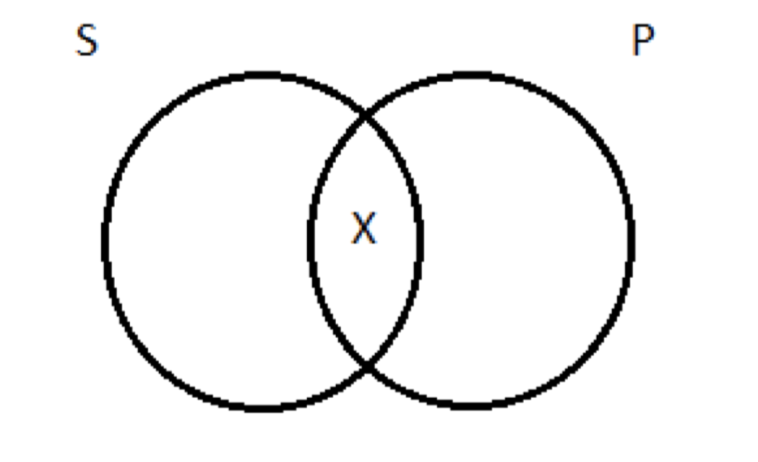
Negativo particular (O)

Este tipo de proposición niega que S esté totalmente incluido en P. Afirma que hay al menos un miembro de S que no es miembro de P. Dado que 'algunos' significa 'hay al menos uno', la expresión canónica de esta proposición es 'Algunas S no son P'—hay al menos un miembro de S que hacen las dos clases no tienen en común. 'Algunos marineros no son piratas' expresa una verdadera proposición negativa particular; 'Algunos perros no son animales' expresa una falsa.

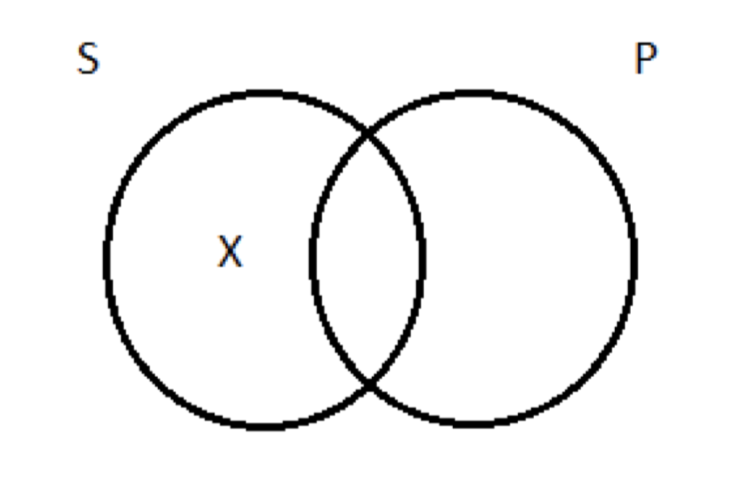
El diagrama de Venn para las proposiciones O es simple. Tenemos que indicar, en nuestra foto, que hay al menos una cosa que está dentro de S, pero fuera de P. Para representar el hecho de que algunos lógicos no son imbéciles, necesitamos poner a Aristóteles (de nuevo, no un imbécil, estoy bastante seguro) dentro del círculo S, sino fuera del círculo P. Al igual que con el diagrama para la proposición I, indicamos la existencia de al menos una cosa dibujando una X en el lugar apropiado:

Una nota sobre terminología

Comúnmente se dice que los cuatro tipos de proposiciones categóricas tienen cada una cantidad y una calidad. Hay dos cantidades: universal y particular. Hay dos cualidades: afirmativa y negativa. Existen cuatro posibles combinaciones de cantidad y calidad, de ahí cuatro tipos de proposición categórica.

Las proposiciones universales —A y E, afirmativas y negativas— son llamadas porque cada una hace una afirmación sobre toda la clase de materias. Si afirmo que todos los vagabundos son bebedores de whisky, he hecho una afirmación que cubre a cada vagabundo, a cada miembro de esa clase. Del mismo modo, si afirmo que no hay pollos son pilotos de carreras, he hecho una afirmación que cubre a todos los pollos, todos no logran conducir autos de carreras.

Las proposiciones particulares —I y O, afirmativas y negativas— en cambio, no hacen afirmaciones sobre cada miembro de la clase de materias. 'Algunos dinosaurios eran herbívoros' solo hace la afirmación de que había al menos un dinosaurio devorador de plantas; no aprendemos de todos los dinosaurios. Observaciones similares se aplican a una proposición O como 'Algunos dinosaurios no eran carnívoros'. Recuerda, 'algunos' solo significa 'al menos uno'.

Las proposiciones afirmativas —A y yo, universales y particulares— hacen afirmaciones afirmativas sobre la relación entre dos clases. A proposiciones afirman la inclusión completa; yo las proposiciones afirman la inclusión parcial. Dato trivial: la palabra latina que significa 'afirmo' es affirmo; la A y la I en esa palabra son de donde provienen los apodos de una letra para los afirmativos universales y particulares.

Las proposiciones negativas —E y O, universales y particulares— hacen afirmaciones negativas sobre la relación entre dos clases. E proposiciones niegan incluso la inclusión parcial; O proposiciones niegan la inclusión completa. Hecho trivial: la palabra latina que significa 'niego' es nego; la E y la O en esa palabra son de donde provienen los apodos de una letra para los negativos universales y particulares.

Forma estándar para oraciones que expresan proposiciones categóricas

Para domar el lenguaje natural, la Lógica Aristotélica se limita a esa porción del lenguaje que expresa proposiciones categóricas. Arriba, dimos frases “canónicas” para cada uno de los cuatro tipos de proposición categórica: 'Todas las S son P' para lo afirmativo universal; 'No S son P' para el negativo universal; 'Algunas S son P' para lo afirmativo particular; y 'Algunas S no son P' para el negativo particular. Estas no son las únicas formas de expresar estas proposiciones en inglés, sino que nos limitaremos a estas formas estándar. Es decir, sólo evaluaremos argumentos cuyas premisas y conclusión se expresen con oraciones con estas formas canónicas.

En términos generales, aquí está la plantilla para oraciones calificadas como forma estándar: [Cuantificador] Subject Term <copula>(not) Predicate Term

Las oraciones de forma estándar comienzan con un cuantificador, una palabra que indica la cantidad de la proposición categórica expresada. Restricción: solo las oraciones que comiencen con 'Todos', 'No' o 'Algunos' califican como forma estándar.

Los términos sujeto y predicado escogen las dos clases involucradas en la proposición categórica. Restricción: los términos sujeto y predicado deben ser sustantivos o frases sustantivas (sustantivos con modificadores) para que una oración esté en forma estándar.

La cópula es una versión del verbo 'ser' ('are', 'is', 'were', 'will be ', etc.). Grado de libertad: no importa qué versión de la cópula se presenta en la oración; puede ser cualquier número o tenso.

'Algunos marineros son pirates' y 'Algunos marineros eran pirates' ambos cuentan como forma estándar, por ejemplo. (La lógica aristotélica es ciega al tenso: presente, pasado, futuro, pasado perfecto, futuro perfecto, futuro perfecto, etc. son todos iguales. A veces la validez de una inferencia depende del tiempo. La Lógica Aristotélica no puede hacer tales juicios. Esta es una de las consecuencias de limitarnos a una porción más simple y precisa del lenguaje natural. Hay lógicas más avanzadas que toman en consideración el tiempo verbal (como era de esperar se les llama “lógicas tensas”), pero ese es un tema para un libro diferente).

La palabra 'no' aparece en la expresión de forma estándar del negativo particular, O proposición: 'Algunos marineros no son piratas'. Restricción: la palabra 'no' sólo puede aparecer en oraciones que expresan O proposiciones; 'no' aparecer con cualquier cuantificador que no sea 'algunos' es una desviación de la forma estándar.

Ahora tenemos una delimitación precisa de la porción del lenguaje natural a la que se restringe la Lógica Aristotélica: sólo oraciones en forma estándar. Pero ahora se agudiza una preocupación que planteamos antes: si solo podemos evaluar argumentos cuyas premisas y conclusiones se expresan con frases de forma estándar, ¿no estamos severamente, quizás ridículamente, limitados? ¿Alguien, alguna vez, fuera de un libro de lógica, expresó así un argumento de la vida real?

Aquí es donde entra en juego la traducción. Muchas oraciones que no están en forma estándar pueden traducirse en oraciones de forma estándar que tienen el mismo significado. El propio Aristóteles creía que todas las proposiciones, sin importar cuán aparentemente complejas o divergentes pudieran analizarse en última instancia como uno de los cuatro tipos de proposiciones categóricas. Aunque esto es, por decirlo suavemente, no una creencia ampliamente arraigada hoy en día, todavía tuvo una enorme influencia en la historia de la lógica, ya que el sistema de Aristóteles fue preeminente por más de dos mil años. Durante ese tiempo, los logísticos desarrollaron procedimientos cada vez más elaborados para analizar una variedad vertiginosa de oraciones de forma no estándar como expresar uno de los cuatro tipos de proposiciones categóricas y traducirlas en consecuencia. Un estudio exhaustivo de esas indagaciones sería agotador, y más allá del alcance de este libro. Bastará con mirar algunos ejemplos simples para hacerse una idea de cuántas expresiones aparentemente desviadas pueden ser tratadas por la Lógica Aristotélica. Nuestro objetivo es simplemente calmar las preocupaciones de que al restringirnos a oraciones de forma estándar estamos limitando severamente el poder de nuestra lógica para evaluar argumentos de la vida real.

Consideremos el primer argumento deductivamente válido que encontramos en este libro, el de Sócrates: Todos los hombres son mortales; Sócrates es un hombre; por lo tanto, Sócrates es mortal. Este argumento tiene tres proposiciones en él, pero ninguna de las tres frases que las expresan está en forma estándar. La primera frase, 'Todos los hombres son mortales', puede parecer que se ajusta a la factura, pero tiene un defecto sutil: 'mortal' es un adjetivo, no un sustantivo. Se requiere que los términos de clase sean sustantivos o frases sustantivas. Pero esta es una solución fácil: agrega una 's' al final y obtienes un sustantivo plural. 'Todos los hombres son mortales' está en forma estándar; expresa una afirmación universal, una proposición. Esta prescripción se aplica de manera general. Los adjetivos predicados pueden reemplazarse con frases sustantivas adecuadas más fácilmente simplemente insertando el sustantivo genérico 'cosas': 'Algunos hombres son guapos' se convierte en 'Algunos hombres son cosas guapas'; 'Ningún sacerdote es tontos' se convierte en 'Ningún sacerdote es tontos'.

Volver al argumento de Sócrates. La segunda premisa también es problemática: 'Sócrates es un hombre'. En primer lugar, no tiene cuantificador. Segundo, su término sujeto, 'Sócrates', elige a una persona individual; se supone que aquí estamos tratando clases, ¿verdad? Bueno, así es, pero en realidad no es un problema. Podemos simplemente hacer de la clase de asignatura una clase de unidad, una clase que contenga exactamente un miembro, a saber, Sócrates. Ahora podemos entender la sentencia como expresando la afirmación de que el miembro único de esa clase también es miembro de la clase de hombres. Es decir, es una afirmación universal— hay toda la inclusión de la clase unitaria Sócrates en la clase de hombres. La frase que necesitamos, entonces, comienza con el cuantificador 'Todos', y para que la gramática funcione, elegimos un sustantivo plural para nombrar a la clase Sócrates: 'Todos los Sócrateses son hombres'. ¿Es 'Sócrateses' el plural de 'Sócrates'? No puedo pensar en nada mejor. En fin, el punto es que esa palabra escoge a una clase que tiene exactamente un miembro, Sócrates. Las oraciones con sujetos singulares pueden ser renderizadas como universales. Si tuviera la frase 'Sócrates no está vivo', podría hacerla como un negativo universal: 'No Sócrateses son seres vivos'.

Hay otras cosas a considerar. El inglés viene con una variedad de palabras cuantificadoras: 'each', 'every', 'any', y así sucesivamente. El sentido común nos dice cómo traducir oraciones con estos a forma estándar: cambiar al cuantificador de forma estándar apropiado: 'todos', 'No' o 'Some'. 'Cada maestro es un trabajador duro' se convierte en 'Todos los maestros son trabajadores duros, por ejemplo. A veces se omiten palabras cuantificadoras, pero queda claro a partir del contexto lo que está pasando. 'Los perros son animales' significa 'Todos los perros son animales'; 'La gente está esperando en línea' se puede representar como 'Algunas personas son cosas que están esperando en línea'. Algunas oraciones tienen un verbo distinto a la cópula. 'Algunas personas comen conejo', por ejemplo, puede traducirse en 'Algunas personas son comedores de conejos'. A veces la palabra 'no' aparece en una oración que tiene un cuantificador distinto de 'algunos'. 'No todos los mamíferos son carnívoros', por ejemplo, puede traducirse en 'Algunos mamíferos no son carnívoros'.

La lista continúa. Como dije, se han realizado siglos de trabajo en la tarea de traducir las oraciones a forma estándar. Podemos detenernos aquí, creo, y simplemente aceptar que la restricción a las oraciones de forma estándar no limita seriamente los argumentos que la Lógica Aristotélica puede evaluar.