4.3: Semántica de la Lógica Sentencial

Nuestra tarea es dar significados precisos a todas las fórmulas bien formadas de SL. Nos referiremos a estos, con bastante sensatez, como “oraciones de SL”. Parte de esta tarea ya está completa. Sabemos algo sobre los significados a las 26 letras mayúsculas: representan frases simples en inglés de nuestra elección. Si bien la semántica para un lenguaje natural como el inglés es complicada (¿Cuál es el significado de una oración? ¿Sus condiciones de verdad? ¿La proposición expresada? ¿Esas dos cosas son iguales? ¿Es algo completamente distinto? Uf.), la semántica para las oraciones SL es simple: todo lo que nos importa es verdad-valor. Una oración en SL puede tener uno de dos valores semánticos: verdadero o falso. Eso es.

Esta es una de las formas en que la mudanza a SL es una domación del lenguaje natural. En SL, cada oración tiene un valor de verdad determinado; y sólo hay dos opciones: verdadera o falsa. El inglés y otros lenguajes naturales son más complicados que esto. Por supuesto, está el tema de las oraciones no declarativas, que no expresan proposiciones y no tienen valores de verdad en absoluto. (Haciendo una breve pausa para señalar, una vez más, que esta charla de oraciones, más que las proposiciones que expresan, tener valores de verdad es un poco rápida y suelta. Reafirmando nuestra postura anterior sobre esto: no es gran cosa.) Pero aunque nos limitemos a frases declarativas en inglés, las cosas no se ven tan simples como lo son en SL. Considera la frase 'Napoleón fue corto'. Quizás no seas consciente de que la concepción popular del emperador francés como diminutivo en estatura tiene sus raíces en la propaganda británica en su momento. De hecho, tenía cerca de 5' 7”. ¿Eso es corto? Bueno, no en su momento (finales del siglo XVIII, principios del XIX); la gente era más baja en ese entonces (la nutrición no era lo que es en estos días, por ejemplo), y así Napoleón estaba aproximadamente promedio o ligeramente por encima. Sin embargo, ahora la gente es más alta, por lo que 5' 7” podría considerarse corto. Al menos, abreviatura de un hombre. Un hombre adulto, es decir. Quiero decir, un hombre adulto que no es un enano. Er, también, un hombre adulto no enano de extracción francesa (sería un hombre alto en Camboya, por ejemplo, donde la estatura promedio es de solo 5' 4”). La estatura promedio para un francés moderno es de 5' 9.25”. Napoleón es 2.25 pulgadas más corto que el promedio. ¿Eso es corto? ¡Diablos, no lo sé!

El problema aquí es que términos relativos como 'corto' tienen casos límite; son vagos. No está claro cómo asignar un valor de verdad a oraciones como 'Napoleón es corto'. Entonces, en inglés, podríamos decir que carecen de un valor de verdad (ausente alguna especificación explícita de los estándares relevantes). Las lógicas más sofisticadas que nuestra SL han desarrollado formas de lidiar con este tipo de casos. En lugar de solo dos valores de verdad, algunas lógicas agregan más. Hay lógicas de tres valores, donde tienes verdadero, falso, y ninguno. Entonces podríamos decir 'Napoleón es bajo' no es ninguno de los dos. Hay lógicas con infinitamente muchos valores de verdad entre verdadero y falso (donde falso es cero y verdadero es 1, y cada número real en el medio es un grado de verdad); en tal sistema, podríamos asignar, no sé, .62 a la proposición de que Napoleón es corto. El punto es que el inglés y otros lenguajes naturales son desordenados cuando se trata de verdad-valor. Los estamos domando en SL asumiendo que cada oración SL tiene un valor de verdad determinado, y que solo hay dos valores de verdad: verdadero y falso, que indicaremos, por cierto, con las letras 'T' y 'F'.

Nuestra tarea desde aquí es proporcionar semántica para los cinco operadores: tilde, punto, cuña, triple barra y herradura (comenzamos con tilde porque es la más simple, y guardamos herradura para el final porque está bastante más involucrada). Especificaremos los significados de estos símbolos en términos de sus efectos sobre el valor de la verdad: ¿cuál es el valor de verdad de una oración compuesta que los presenta como operador principal, dados los valores de verdad de los componentes? Los valores semánticos de los operadores serán funciones de verdad: relatos sistemáticos de las salidas de verdad-valor (de la oración compuesta) resultantes de las posibles entradas de verdad-valor (de los componentes más simples).

Negaciones (TILDE)

Debido a que tilde es un operador de un solo lugar, este es el operador más simple de tratar. La forma general de una negación es ~ p, donde 'p' es una variable que representa cualquier oración SL genérica, simple o compuesta. Como letra minúscula, 'p' no es parte de nuestro lenguaje (SL); más bien, es una herramienta que usamos para hablar de nuestro lenguaje, para referirse a construcciones genéricas bien formadas dentro de ella.

Tenemos que dar cuenta del significado de la tilde en términos de su efecto sobre el valor de la verdad. Tilde, como decíamos, es el equivalente SL de 'no' o 'no es así que eso'. Pensemos en lo que sucede en inglés cuando usamos esos términos. Si tomamos una frase verdadera, decimos 'Edison inventó la bombilla', y formamos un compuesto con ella y 'no', obtenemos 'Edison no inventó la bombilla', una falsedad. Si tomamos una frase falsa, como 'James Brown está vivo', y la negamos, obtenemos 'James Brown no está vivo', una verdad.

Evidentemente, el efecto de la negación sobre el valor de la verdad es convertir una verdad en una falsedad, y una falsedad en una verdad. Podemos representar esto gráficamente, usando lo que llamaremos una “tabla de verdad”. La siguiente tabla da una especificación completa de la semántica de tilde:

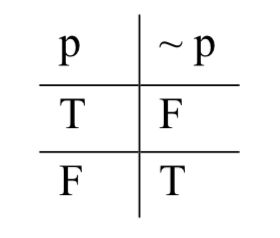
En la columna de la izquierda, tenemos 'p', que, como variable, significa una oración SL genérica, no especificada. Como no está especificado, no conocemos su verdad-valor; pero como es una oración en SL, sí sabemos que solo hay dos posibilidades para su verdad-valor: true o false (T o F). Entonces, en la primera columna, enumeramos esas dos posibilidades. En la segunda columna, tenemos '~ p', la negación de lo que sea que sea 'p'. Podemos calcular el verdad-valor de la negación con base en el verdad-valor de la oración que se está negando: si la oración original es verdadera, entonces su negación es falsa; si la oración original es falsa, entonces la negación es verdadera. Esto es lo que representamos cuando escribimos 'F' y 'T' debajo de la tilde (el operador que efectúa el cambio en el valor de verdad) en la segunda columna, en las mismas filas que sus opuestos.

Tilde es un operador de verdad funcional. Su significado está especificado por una función: si ingresas una T, la salida es una F; si ingresas una F, la salida es una T. Los otros cuatro operadores también se definirán en términos de la función-verdad que representan. Esto es exactamente análogo, de nuevo, a la aritmética. La suma, con su operador '+', es una función sobre los números. Entrada 1 y 3, y la salida es 4. En SL, sólo tenemos dos valores —T y F— pero es el mismo tipo de cosas. También podríamos usar números para representar los valores de verdad: 0 para falso y 1 para verdadero, por ejemplo. En ese caso, tilde sería una función que emite 0 cuando 1 es la entrada, y salidas 1 cuando 0 es la entrada.

Conjunciones (DOT)

Nuestra caracterización aproximada de las conjunciones fue que son frases 'y', frases como 'Beyoncé es lógico y James Brown está vivo'. Dado que este tipo de oraciones compuestas involucran dos componentes más simples, decimos que el punto es un operador de dos lugares. Entonces, cuando especificamos la forma general de una conjunción usando variables genéricas, necesitamos dos de ellas. La forma general de una conjunción en SL es p • q. Las preguntas que necesitamos responder son estas: ¿Bajo qué circunstancias es verdadera toda la conjunción, y bajo qué circunstancias es falsa? ¿Y cómo depende esto de los valores de verdad de las partes componentes?

Antes remarcamos que cuando alguien pronuncia una conjunción, se está comprometiendo con ambas de las conjunciones. Si te digo que Beyoncé es sabia y James Brown está vivo, me estoy comprometiendo con la verdad de ambos hechos alegados; estoy, por así decirlo, prometerte que ambas cosas son ciertas. Entonces, si incluso uno de ellos resulta falso, he roto mi promesa; la única forma en que se cumple la promesa es si ambas resultan ser ciertas.

Así funcionan las conjunciones, entonces: son ciertas por si acaso ambas conjunciones son verdaderas; falsas de lo contrario. Podemos representar esto gráficamente, con una tabla de verdad que define el punto:

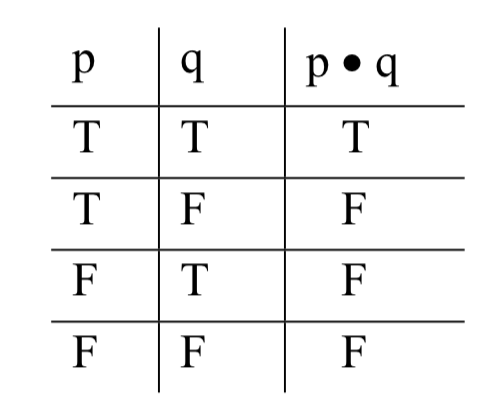
Dado que el punto es un operador de dos lugares, necesitamos columnas para cada una de las dos variables en su forma general, p y q. Cada una de ellas es una oración SL genérica que puede ser verdadera o falsa. Eso nos da cuatro posibilidades para sus valores de verdad como par: ambos true, p true y q false, p false y q true, ambos false. Estas cuatro posibilidades nos dan las cuatro filas de la tabla. Para cada una de estas posibles entradas a la verdad-función, obtenemos una salida, listada debajo del punto. T es la salida cuando ambas entradas son Ts; F es la salida en cualquier otra circunstancia.

Disyunción (CUÑA)

Nuestra caracterización aproximada de las disyunciones fue que son oraciones “o”, frases como 'Beyoncé es lógico o James Brown está vivo'. En SL, la forma general de una disyunción es p osé q. Necesitamos averiguar las circunstancias en las que tal compuesto es verdadero; necesitamos la verdad-función representada por la cuña.

En este punto nos enfrentamos a una complicación. Se supone que Wedge capta la esencia de 'o' en inglés, pero la palabra 'o' tiene dos sentidos distintos. Este es uno de esos casos en los que el lenguaje natural necesita ser domesticado: nuestra cuña solo puede tener un significado, por lo que debemos elegir entre los dos sentidos alternativos de la palabra inglesa 'or'.

'O' se puede utilizar exclusiva o inclusivamente. El sentido exclusivo de 'o' se expresa en una frase como esta: 'Clinton ganará las elecciones o Trump ganará la elección'. Los dos disjuntos presentan posibilidades exclusivas: uno u otro sucederá, pero no ambos. El sentido inclusivo de 'o', sin embargo, permite la posibilidad de ambos. Si te dijera que estaba teniendo problemas para decidir qué pedir en un restaurante, y dijera: “Voy a pedir langosta o bistec”, y luego terminé decidiendo por conseguir el surf 'n' turf (langosta y bistec combinados en el mismo plato principal), no dirías que te había mentido cuando dije que pediría langosta o bistec. El sentido inclusivo de 'o' permite uno u otro, o ambos.

Usaremos el sentido inclusivo de 'o' para nuestra cuña. Hay argumentos para elegir el sentido inclusivo sobre el exclusivo, pero no vamos a detenernos en los de aquí. (Como fue el caso cuando tuvimos que elegir la palabra 'algunos' en la lógica aristotélica, el argumento sostiene que el sentido inclusivo es el significado central de 'o', y el sentido exclusivo es un significado que a menudo, pero no siempre, se trasmite cuando usamos 'o' en determinadas circunstancias—una implicación. Esta línea de razonamiento tiene tanto adherentes como detractores.) Tenemos que elegir un significado para cuña, y estamos eligiendo el sentido inclusivo de 'o'. Como veremos más adelante, el sentido exclusivo no nos va a perder por esta elección: podremos simbolizar 'o' exclusivos dentro de SL, utilizando una combinación de operadores.

Entonces, cuña es inclusiva 'o'. Es cierto cuando una u otra —o ambas— conjunciones es verdadera; falsa de otra manera. Esta es su definición de tabla de verdad:

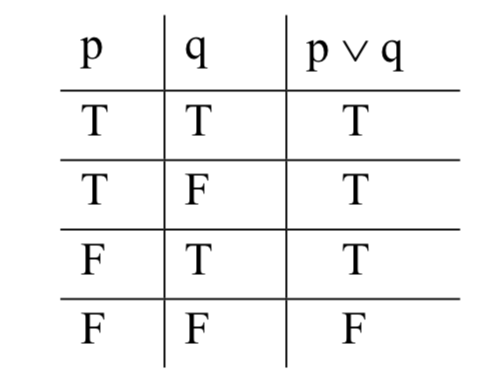
Bicondicionales (TRIPLE-BAR)

Como decíamos, los bicondicionales son, más o menos, 'si y sólo si' frases como 'Beyoncé es lógico si y sólo si James Brown está vivo'. 'Si y solo si' no es una frase que la mayoría de la gente usa en la vida cotidiana, sino que el significado es sencillo: se usa para afirmar que ambos componentes tienen el mismo valor de verdad, que uno conlleva el otro y viceversa, que no pueden tener valores de verdad diferentes. En SL, la forma general de un bicondicional es p ≡ q. Esta es la verdad-función:

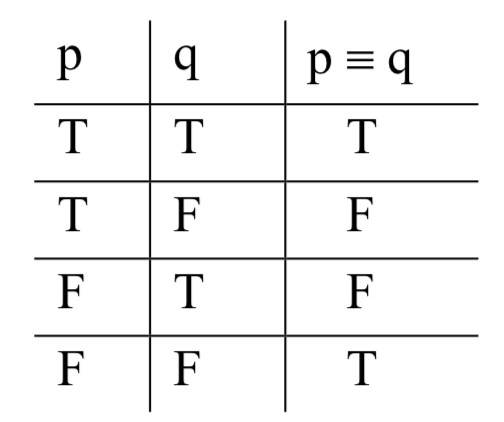
La triple barra es como un signo lógico igual (incluso se parece a '='): la función entrega una salida de T cuando ambos componentes son iguales, F cuando no lo son.

Si bien el significado verdad-funcional de triple barra ahora es claro, todavía puede darse el caso de que el significado intuitivo de la frase inglesa 'si y solo si' siga siendo esquivo. Esto es natural. No temas: tendremos mucho más que decir sobre esa locución cuando discutamos la traducción entre inglés y SL; una comprensión completa de los bicondicionales solo se puede lograr a partir de una comprensión plena de los condicionales, a lo que, como sugieren los nombres, están de cerca relacionados. Pasamos ahora a una especificación del significado verdad-funcional de este último.

Condicionales (HERRADURA)

Nuestra caracterización aproximada de los condicionales fue que son frases 'si/entonces' —frases como 'Si Beyoncé es lógico, entonces James Brown está vivo'. Usamos este tipo de oraciones todo el tiempo en el habla cotidiana, pero es sorprendentemente difícil precisar el significado preciso del condicional, especialmente dentro de las limitaciones impuestas por SL. De hecho, hay muchos relatos en competencia de lo condicional, muchos condicionales diferentes para elegir, en una literatura que se remonta a los estoicos de la antigua Grecia. Los libros enteros pueden estar —y haber sido— escritos sobre el tema de los condicionales. En el transcurso de nuestra discusión sobre la semántica para herradura, vamos a tener una idea de por qué este es un tema tan molesto; es complicado.

La forma general de un condicional en SL es p q. Tenemos que decidir para qué valores de p y q el condicional resulta verdadero y falso. Para ayudarnos (haciendo las cosas más vívidas), consideraremos una afirmación condicional real, con una pequeña historia para acompañarla. Supongamos que Barb sufre de dolor en las articulaciones; tal vez sea gota, tal vez sea artritis, no lo sabe y no ha ido al médico para averiguarlo. Se queja de su dolor a su vecina, Sally. Sally es una gran creyente en la “medicina alternativa” y la “curación holística”. Después de escuchar una breve descripción de los síntomas, Sally está lista con una receta, que entrega a Barb en forma de reclamo condicional: “Si bebes este té de hierbas todos los días durante una semana, entonces tu dolor desaparecerá”. Ella entrega un paquete de hojas de té e instruye a Barb en su correcta preparación.

Queremos evaluar la afirmación condicional de Sally —que si Barb bebe el té de hierbas diariamente durante una semana, entonces su dolor desaparecerá— por la verdad/falsedad. Para ello, consideraremos diversos escenarios, cuyos detalles se basarán en esa evaluación.

Escenario #1: Barb de hecho bebe el té todos los días durante una semana según lo prescrito, y, después de hacerlo, he aquí, su dolor se ha ido. ¡Sally tenía razón! En este escenario, diríamos que el condicional que estamos evaluando es cierto.

Escenario #2: Barb hace lo que dijo Sally y bebe el té todos los días durante una semana, pero, una vez terminada la semana, el dolor permanece, igual que siempre. En este escenario, diríamos que Sally se equivocó: su consejo condicional era falso.

Quizá pueda ver lo que estoy haciendo aquí. Cada uno de los escenarios representa una de las filas en la definición de tabla de verdad para la herradura. La afirmación condicional de Sally tiene un antecedente: Barb bebe el té todos los días durante una semana, y un consecuente, el dolor de Barb desaparece. Estos son p y q, respectivamente, en el condicional p q. En el escenario #1, tanto p como q eran ciertos: Barb sí bebió el té, y el dolor sí se fue; en el escenario #2, p era cierto (Barb bebió el té) pero q era falso (el dolor no se fue). Estos dos escenarios son las dos primeras filas de las tablas de verdad de cuatro filas que ya hemos visto para punto, cuña y triple barra. Para herradura, la función de verdad nos da T en la primera fila y F en la segunda:

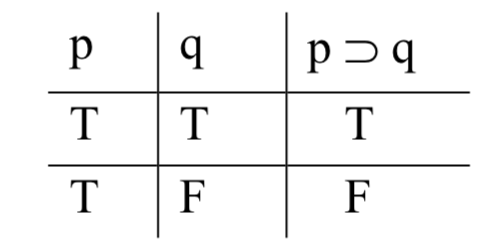
Todo lo que queda es averiguar qué sucede en la tercera y cuarta filas de la tabla, donde el antecedente (p, Barb bebe el té) es falso ambas veces y el consecuente es primero verdadero (en la fila 3) y luego falso (en la fila 4). Hay dos escenarios más a considerar.

En el escenario #3, Barb decide que Sally es un poco chiflada, o bebe el té una vez y sabe horrible así que decide dejar de beberlo—sean cuales sean las circunstancias, Barb no bebe el té durante una semana; el antecedente es falso. Pero en este escenario, resulta que una vez terminada la semana, el dolor de Barb se ha ido; lo consecuente es cierto. ¿Qué decimos del consejo de Sally —si tomas el té, el dolor desaparecerá— en este conjunto de circunstancias?

En el escenario #4, nuevamente Barb no bebe el té (falso antecedente), y una vez terminada la semana, el dolor permanece (falso consecuente). ¿Qué decimos de los consejos condicionales de Sally en este escenario?

Es tentador decir que en los escenarios 3 y 4, ya que Barb ni siquiera probó el remedio de Sally, no estamos en condiciones de evaluar los consejos de Sally en busca de verdad o falsedad. Ni siquiera se puso a prueba la hipótesis. Entonces, nos inclinamos a decir 'Si bebes el té, entonces el dolor desaparecerá' no es ni verdadero ni falso. Pero si bien esta podría ser una opción viable en inglés, no funcionará en SL. Hemos hecho las suposiciones simplificadoras de que toda sentencia SL debe tener un valor de verdad, y que las únicas dos posibilidades son verdaderas y falsas. No podemos decir que no tiene verdad-valor; no podemos agregar un tercer valor y llamarlo “ninguno”. Tenemos que poner una T o una F debajo de la herradura en la tercera y cuarta filas de la tabla de la verdad para ese operador. Dada esta restricción, y dado que ya hemos decidido cómo deberían funcionar las dos primeras filas, hay cuatro formas posibles de especificar la función de verdad para herradura:

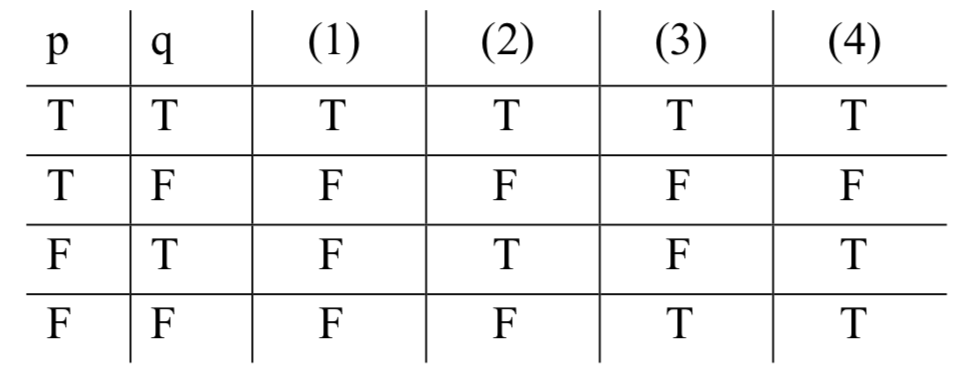
Estas son nuestras únicas opciones (recuerde, las dos primeras filas están asentadas; los escenarios 1 y 2 anteriores tuvieron resultados claros). ¿Cuál capta mejor el significado del condicional?

La opción 1 es tentadora: como señalamos, en las filas 3 y 4, la hipótesis de Sally ni siquiera se prueba. Si nos vemos obligados a elegir entre verdadero y falso, bien podríamos ir con falso. El problema con esta opción es que esta función de verdad—true cuando ambos componentes son verdaderos; false de otro modo— ya está tomada. Ese es el significado de punto. Si elegimos la opción 1, hacemos herradura y punto significan lo mismo. Eso no va a funcionar: son operadores diferentes; deberían tener diferentes significados. 'Y' y 'si/then' no significan lo mismo en inglés, claramente.

La opción 2 también tiene sus encantos. Bien, podríamos decir, en ninguna de las dos situaciones se prueba la hipótesis de Sally, pero al menos la fila 3 tiene algo a su favor, Sally sabio: el dolor desaparece. Entonces digamos que su condicional es cierto en ese caso, pero falso en la fila 4 cuando todavía hay dolor. Nuevamente, esto no va a hacer. Compara la columna bajo la opción 2 con la columna bajo q. Son iguales: T, F, T, F. Eso significa que todo el condicional, p q, tiene el mismo significado que su consecuente, llano viejo q. No es bueno. El antecedente, p, no hace diferencia al verdad-valor del condicional en este caso. Pero debería; no deberíamos ser capaces de calcular el valor de verdad de una función de dos posiciones sin siquiera mirar una de las entradas.

La opción 3 es la siguiente. A algunas personas les parece razonable decir que el condicional es falso en la fila 3: hay algo en la desaparición del dolor, a pesar de no beber el té, eso es incompatible con la predicción de Sally. Y si no podemos poner una F en la última fila también (esto es solo la opción 1 otra vez), entonces hazla una T. Pero esto falla por la misma razón que lo hizo la opción 1: la verdad-función ya está tomada, esta vez por la triple barra. 'Si y sólo si' es un reclamo mucho más fuerte que el mero 'si/entonces'; los bicondicionales deben tener un significado diferente de los meros condicionales.

Eso deja la opción 4. Esta es la que adoptaremos, sobre todo porque es la única posibilidad que queda. El condicional es cierto cuando tanto antecedente como consecuente son ciertos —escenario 1; es falso cuando el antecedente es verdadero pero el consiguiente falso—escenario 2; y es cierto siempre que el antecedente es falso —escenarios 3 y 4. Esta es la definición de herradura:

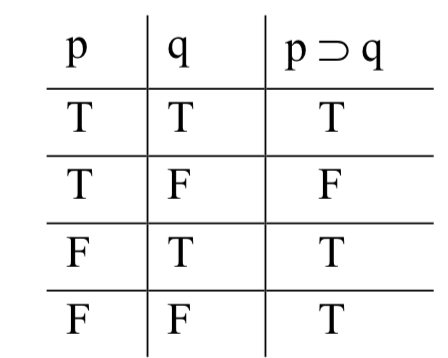
No es lo ideal. Las dos primeras filas son bastante plausibles, pero hay algo profundamente extraño en decir que la frase 'Si bebes el té, entonces el dolor desaparecerá' es cierta siempre que no se bebe el té. Sin embargo, esa es nuestra única opción. Quizás podamos hacerlo un poco más apetecible diciendo —como hicimos sobre proposiciones categóricas universales con clases de materias vacías— que si bien es cierto en tales casos, solo es cierto de manera vacía o trivial, cierto de una manera que no te dice cómo son las cosas en el mundo.

Lo que también puede ayudar un poco es señalar que si bien las filas 3 y 4 no tienen mucho sentido para el caso Barb/Sally, sí funcionan para otros condicionales. El autor de terror Stephen King vive en Maine (la mitad de sus libros están ambientados ahí, parece). Considera esto condicional: 'Si Stephen King es el gobernador de Maine, entonces vive en Maine'. Si bien es un ciudadano prominente, King no es el gobernador de Maine, por lo que el antecedente es falso. Él es, sin embargo, como hemos señalado, un residente de Maine, por lo que lo consecuente es cierto. Estamos en la fila 3 de la tabla de la verdad para condicionales aquí. E intuitivamente, el condicional es cierto: él no es el gobernador, pero si lo fuera, viviría en Maine (los gobernadores residen en las capitales de sus estados). Y consideremos esto condicional: 'Si Stephen King es presidente de Estados Unidos, entonces vive en Washington, DC'. Ahora tanto el antecedente (King es presidente) como el consecuente (vive en DC) son falsos: estamos en la fila 4 de la mesa. Pero una vez más, el reclamo condicional es intuitivamente cierto: si fuera presidente, viviría en DC.

Observe el truco que tiré ahí: cambié del llamado estado de ánimo indicativo (si lo es) al subjuntivo (si lo fuera). La verdad del condicional es más clara en este último estado de ánimo que el primero. Pero este truco no siempre va a funcionar para que el condicional se haga realidad en la tercera y cuarta filas. Considera: 'Si Stephen King fuera presidente de Estados Unidos, entonces viviría en Maine' y 'Si Stephen King fuera gobernador de Maine, entonces viviría en Washington, DC'. Estos son ejemplos de tercera y cuarta fila, respectivamente, pero ninguno es intuitivamente cierto.

A estas alturas tal vez se esté dando una idea de por qué los condicionales son un tema tan molesto en la historia de la lógica. A lo largo de los siglos (y especialmente en el siglo pasado) se han desarrollado una variedad de enfoques, con formalismos lógicos alternativos asociados, para hacer frente a los diversos problemas que surgen en relación con las reivindicaciones condicionales. El nuestro es el enfoque más sencillo, con el que comenzar. Al tratarse de un texto introductorio, esto es apropiado. Puedes investigar relatos alternativos del condicional si extiendes aún más tu estudio de lógica.

Computación de Verdad-Valores de Sentencias Compuestas SL

Con las definiciones verdad-funcionales de los cinco operadores SL en la mano, podemos desarrollar una habilidad preliminar que será necesaria para desplegar cuando llegue el momento de probar los argumentos de SL para su validez. Necesitamos ser capaces de calcular los valores de verdad de las oraciones SL compuestas, dados los valores de verdad de sus partes más simples (las oraciones simples, letras mayúsculas). Para ello, primero debemos determinar a qué tipo de oración compuesta estamos tratando: negación, conjunción, disyunción, condicional o bicondicional. Esto implica decidir cuál de los operadores en la sentencia SL es el operador principal. Luego calculamos el valor de verdad del compuesto de acuerdo con la definición para el operador apropiado, utilizando los valores de verdad de los componentes más simples. Si estos componentes son ellos mismos compuestos, determinamos sus operadores principales y calculamos en consecuencia, en términos de sus componentes más simples, repitiéndose según sea necesario hasta llegar a los componentes más simples de todos, las letras mayúsculas. Algunos ejemplos dejarán claro el proceso.

Supongamos que A y B son verdaderas oraciones SL. Considera este compuesto:

~ A

¿Cuál es su verdad-valor? Para responder a esa pregunta, primero tenemos que averiguar a qué tipo de oración compuesta estamos tratando. Tiene dos operadores—la tilde y la cuña. ¿Cuál de estos es el principal operador; es decir, tenemos una negación o una disyunción? Respondimos a esta pregunta antes, cuando estábamos discutiendo la sintaxis de SL. Nuestra convención con tildes es que niegan la primera construcción bien formada inmediatamente a su derecha. En este caso, 'A' es la primera construcción bien formada inmediatamente a la derecha de la tilde, por lo que la tilde la la niega. Eso significa que wedge es el operador principal; esto es una disyunción, donde el disjunto de la izquierda es ~ A y el disjunto de la derecha es B. Para calcular el valor de verdad de la disyunción, necesitamos conocer los valores de verdad de sus disyuntores. Sabemos que B es verdad; necesitamos conocer el valor de verdad de ~ A. Eso es fácil, ya que A es cierto, ~ A debe ser falso. Es útil realizar un seguimiento de los cálculos paso a paso de esta manera:

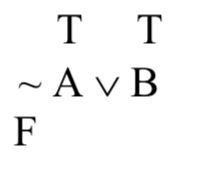
He marcado los valores de verdad de los componentes más simples, A y B, encima de esas letras. Entonces, bajo la tilde, el operador que lo hace suceder, escribo 'F' para indicar que el disjunto de la izquierda, ~ A, es falso. Ahora puedo calcular el verdad-valor de la disyunción: el disyuntor de la izquierda es falso, pero el disjunto de la derecha es cierto; esta es la fila 3 de la tabla de verdad de cuña, y la disyunción resulta cierta en ese caso. Esto lo indico con una 'T' debajo de la cuña, que destaco (con negritas y subrayado) para enfatizar el hecho de que este es el verdad-valor de toda la frase compuesta:

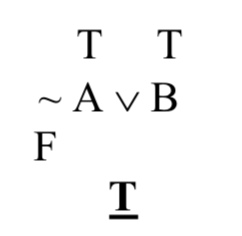
Cuando estábamos discutiendo la sintaxis, afirmamos que agregar paréntesis a un compuesto como el último alteraría su significado. Ahora estamos en condiciones de probar esa afirmación. Considera esta frase SL (donde A y B se asumen de nuevo como verdaderas):

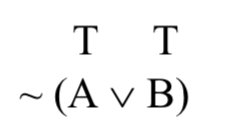
Ahora el operador principal es la tilde: niega toda la disyunción dentro de los paréntesis. Para descubrir el efecto de esa negación sobre el valor de la verdad, necesitamos calcular el valor de verdad de la disyunción que niega. Tanto A como B son ciertas; esta es la fila superior de la tabla de verdad de cuña; las disyunciones resultan verdaderas en tales casos:

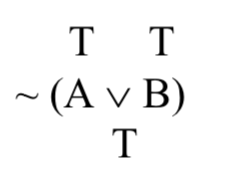
Entonces la tilde está negando una verdad, dándonos una falsedad:

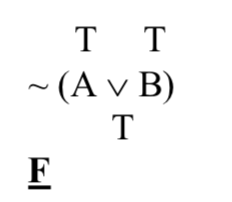
El verdad-valor del todo es falso; la disyunción de aspecto similar sin los paréntesis era verdadera. Estas dos oraciones SL deben tener diferentes significados; tienen diferentes valores de verdad.
Quizás sea útil mirar un ejemplo más, esta vez de una sentencia SL más compleja. Supongamos nuevamente que A y B son verdaderas oraciones simples SL, y que X e Y son falsas oraciones simples SL. Vamos a calcular el valor de la verdad de la siguiente oración compuesta:

~ (A • X) (B)

Como primer paso, es útil marcar los valores de verdad de las oraciones simples:

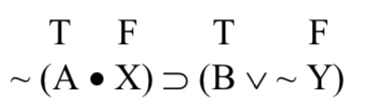
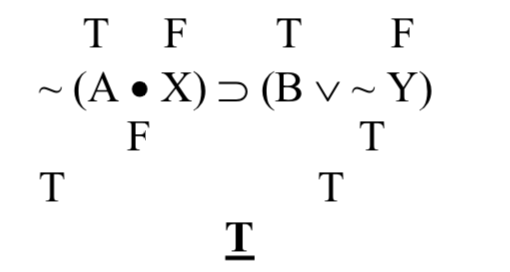
Ahora, tenemos que averiguar qué tipo de oración compuesta es esta; ¿cuál es el operador principal? Esta frase es condicional; el operador principal es la herradura. La tilde en el extremo izquierdo niega la primera construcción bien formada inmediatamente a su derecha. En este caso, es decir (A • X). ~ (A • X) es el antecedente de este condicional; (B ‖ ~ Y) es el consecuente. Necesitamos calcular los valores de verdad de cada uno de estos antes de poder calcular el valor de verdad de todo el compuesto.

Tomemos primero el antecedente, ~ (A • X). La tilde niega la conjunción, así que antes de que podamos saber qué hace la tilde, necesitamos conocer el verdad-valor de la conjunción dentro de los paréntesis. Las conjunciones son verdaderas por si acaso ambas conjunciones son verdaderas; en este caso, A es verdadera pero X es falsa, por lo que la conjunción es falsa, y su negación debe ser verdadera:

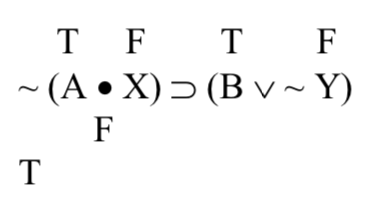
Entonces el antecedente de nuestro condicional es cierto. Echemos un vistazo a lo consecuente, (B ‖ ~ Y). Y es falso, así que ~ Y debe ser verdad. Eso significa que ambos disjuntos, B y ~ Y son ciertos, haciendo que nuestra disyunción sea cierta:

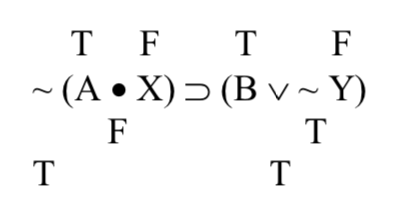
Tanto el antecedente como el consecuente del condicional son ciertos, por lo que todo el condicional es cierto:

Una nota final: a veces solo se necesita información parcial para hacer un juicio sobre el valor de verdad de una oración compuesta. Vuelva a mirar las definiciones de la tabla de verdad de los operadores de dos lugares:

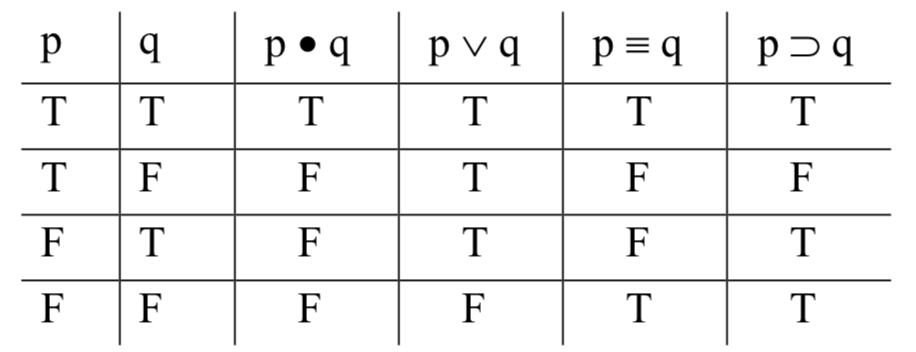
Para tres de estos operadores—el punto, la cuña y la herradura— una de las hileras no es como las otras. Para el punto: solo sale verdad cuando tanto p como q son verdaderas, en la fila superior. Para la cuña: solo sale falso cuando tanto p como q son falsas, en la fila inferior. Para la herradura: solo sale falso cuando p es verdadero y q es falso, en la segunda fila.

Notar esto nos permite, en algunos casos, calcular los valores de verdad de los compuestos sin conocer los valores de verdad de ambos componentes. Supongamos de nuevo que A es verdadera y X es falsa; y que Q sea una simple oración SL cuyo valor de verdad es un misterio para ti (tiene uno, como todos ellos deben; simplemente no te estoy diciendo qué es). Considera este compuesto:

A

Sabemos que uno de los disjuntos es cierto; no conocemos el verdad-valor del otro. ¡Pero no necesitamos! Una disyunción sólo es falsa cuando ambos de sus desjuntos son falsos; es cierto cuando incluso uno de sus disjuntos es cierto. Un ser verdadero es suficiente para decirnos que la disyunción es cierta; Q no importa.

Considera la conjunción:

X • Q

Sólo conocemos el verdad-valor de una de las conjunciones: X es falso. Eso es todo lo que necesitamos saber para calcular la verdad-valor de la conjunción. Las conjunciones sólo son ciertas cuando ambas de sus conjunciones son verdaderas; son falsas cuando incluso una de ellas es falsa. X ser falso es suficiente para decirnos que esta conjunción es falsa.

Por último, considere estos condicionales:
Q A y X Q

Ambos son ciertos. Los condicionales solo son falsos cuando el antecedente es verdadero y el consecuente es falso; así son verdaderos siempre que lo consecuente sea verdadero (como es el caso en Q A) y siempre que el antecedente sea falso (como es el caso en X Q).

Ejercicios

Calcular los valores de verdad de las siguientes oraciones compuestas, donde A, B y C son verdaderos; X, Y y Z son falsos; y P y Q son de valor de verdad desconocido.