27.2: Imaginando la estructura lógica
- Page ID
- 93772
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Así como un buen plano puede ayudarnos a visualizar la distribución o estructura espacial de una casa, un buen diagrama puede ayudarnos a comprender la disposición o estructura lógica de una oración o un argumento. En efecto (como veremos más adelante), en algunos casos cuando dibujamos la imagen de las premisas de un argumento, la conclusión se saca automáticamente en el proceso.
Considera los dos argumentos muy simples a continuación:
P1. Todos los humanos son mortales.
P2. Wilbur es humano.
Entonces, Wilbur es mortal.
P1. Todos los números pares son divisibles por 2.
P2. 18 es un número par.
Asi que, 18 es divisible por 2.
Los dos argumentos tienen un contenido o tema muy diferente (mortalidad humana vs. números), pero también tienen algo muy importante en común. Ambos son válidos, y son válidos por la misma razón. Como siempre, la validez se basa en la forma o estructura, más que en el contenido o la materia, y estos dos argumentos tienen la misma estructura lógica. Podemos representar esta estructura común borrando el contenido y simplemente dejando atrás el esqueleto lógico:
P1. Todos ____son____.
P2. x es un _____.
Entonces, x es un _____.
No importa cómo conectemos el contenido a estos espacios en blanco, si conectamos la misma palabra o frase en el mismo marcador de posición cada vez que ocurre, y el resultado es una oración gramatical, el argumento resultante será válido.
En el mejor de los casos, puedes hacer un dibujo del local y encontrarás que tu foto, sin más adiciones, también incluye una imagen de la conclusión. Este es el caso en algunos de los ejemplos más simples de argumentos deductivamente válidos. En efecto, en estos casos, los maestros suelen dibujar un cuadro para convencer a sus alumnos de que un formato de argumento determinado es válido.
Ayudará si imaginamos construir una imagen de esta estructura de argumentos paso a paso (ver Figura 27.2.1). Comenzamos dibujando la primera premisa, poniendo un círculo más pequeño que representa a los humanos completamente dentro de un círculo más grande que representa criaturas que son mortales (en la subfigura de la izquierda).
A continuación, dibujamos la segunda premisa colocando una letra que representa a Wilbur en el segundo círculo (en la subfigura media).
Por último, tenemos que sacar la conclusión. Pero encontramos que al dibujar las dos premisas, ya sacamos la conclusión. Esto ocurrió porque el argumento es válido, y como vimos antes, la información en la conclusión ya está contenida en las premisas. Dado que la información en la conclusión ya está en las instalaciones, nuestra representación de los locales contendrá automáticamente una representación de la conclusión.
Los diagramas izquierdo y central de la Figura 27.2.1 ya son abstractos, pero en el diagrama del extremo derecho eliminamos el último bit de contenido. Esto deja solo una imagen de la forma del argumento. Ahora es fácil ver que —y por qué— cualquier argumento con esta forma debe ser válido. Algunas frases y argumentos no se prestan a una representación gráfica, pero muchos sí, y para los que lo hacen, las imágenes pueden ser muy útiles. Por supuesto, este es un ejemplo fácil, y realmente no necesitamos un diagrama para entenderlo. Pero las imágenes realmente se vuelven propias cuando recurrimos a problemas más difíciles o complejos que pueden ser difíciles de captar sin imágenes (veremos un ejemplo a continuación con el problema de selección de tarjeta).
.png)
Condicionales y Argumentos condicionales
Condiciones necesarias y suficientes
Pensar en términos de frecuencias o proporciones no sólo nos ayuda a aclarar las probabilidades. También a veces puede ayudarnos a razonar sobre los condicionales. Toma el condicional:
- Si Fido es un perro, entonces es un mamífero.
Esta frase trata sobre un perro específico, Fido, más que sobre grupos de cualquier tipo. Pero muchos (no todos) condicionales como este son verdaderos (o falsos) por hechos sobre grupos. Aquí, el hecho de que todos los perros sean mamíferos.
.png)
Podemos representar esta afirmación con un diagrama como el de la Figura 27.2.2, y luego podemos usarlo para ayudarnos en nuestro razonamiento. Podemos colocar el punto que representa a Fido en el círculo canino, e inmediatamente queda claro que está en el círculo de mamíferos.
Hasta el momento, las cosas son obvias. Nuestro diagrama también nos muestra por qué varias frases más complicadas son verdaderas o falsas. Por ejemplo, si colocamos el punto de Fido en cualquier lugar fuera del círculo de mamíferos, digamos en la ubicación Z, no hay forma de que pueda estar en el círculo canino. Entonces, el condicional:
Si Fido no es un mamífero, entonces no es un perro.
también es cierto.
Ahora volvamos a la Figura 27.2.2 para ver cómo funcionan las condiciones necesarias y suficientes.
- Si algo está dentro del más pequeño, perro, círculo, entonces debe estar dentro del círculo más grande, mamífero,. Estar en el círculo más pequeño es suficiente —todo lo que se necesita— para estar dentro del círculo exterior. Dado que X es un perro, X es un mamífero.
- Si algo está fuera del círculo exterior, no hay manera de que pueda estar dentro del círculo interno. Como muestra Y, estar en el círculo más grande no es suficiente para estar en el más pequeño, pero es necesario.
En aquellos casos en los que podemos pensar en condicionales en términos de conjuntos de cosas, el conjunto (e.g., perros) mencionado en el antecedente es el círculo interno y el conjunto (e.g., mamíferos) mencionado en el consiguiente es el círculo exterior. Esto deja claro pictóricamente por qué los antecedentes son condiciones suficientes y las consecuentes son condiciones necesarias.
Esto es posible en muchos casos donde puede ser menos obvio. Considerar:
- Si mi alarma se rompe mañana, perderé mi vuelo.
Podemos pensar en esto como decir: en todas las ocasiones en las que mi alarma no sonó, perdería mi vuelo. Esto es así, de todos modos, en todas las ocasiones normales que probablemente surjan. Entonces podemos dibujar una imagen del tipo familiar, con el círculo que contiene las ocasiones en las que mi alarma se rompe dentro del círculo de las ocasiones en las que pierdo mi vuelo.
Cuando cometemos la falacia de afirmar lo consecuente (3.3), estamos argumentando como si estar en el círculo más grande sea suficiente para asegurar estar en el más pequeño. Pero la ubicación de Y en la Figura 27.2.2 de la página anterior muestra que esto es incorrecto. Y cuando cometemos la falacia de negar el antecedente (3.3), estamos argumentando como si no estar en el círculo más pequeño sea suficiente para asegurar no estar en el más grande. Nuevamente, Y muestra que esto no es válido. Todo está bastante claro cuando nos apegamos a perros y mamíferos, pero ahora veremos un caso que mucha gente encuentra confuso.
La tarea de selección de tarjetas
Uno de los ejercicios del capítulo sobre condicionales fue así:
Wilbur tiene un paquete de cartas, cada una de las cuales tiene una letra [ya sea una consonante o una vocal] en un lado y un número [par o impar] en el otro. Algunas de las cartas están tumbadas sobre una mesa (Figura 27.2.3). Qué cartas debes entregar para probar la hipótesis:
Hipótesis: Si una carta tiene una vocal en un lado, entonces tiene un número impar en el otro.
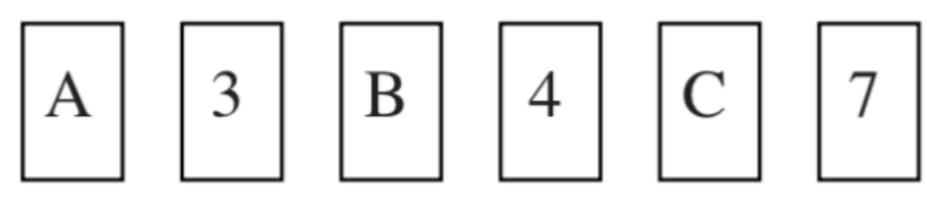.png)
Pista: solo dos de los cuatro tipos de etiquetas son relevantes. El problema puede resultar confuso, pero una vez que dibujamos un cuadro que representa la hipótesis, las cosas se vuelven más fáciles. La hipótesis significa que si alguna carta tiene una vocal en un lado entonces tiene un número impar en el otro, por lo que está afirmando que todas las cartas con vocales en un lado tienen números impares en el otro. Y sabemos dibujar una imagen de esto, lo que hacemos en la Figura 27.2.4.
.png)
Tenga en cuenta que la hipótesis sólo dice que todas las vocales tienen números impares en el otro lado. No dice nada sobre lo que tienen los números impares del otro lado, y no dice nada de lo que tienen las consonantes del otro lado. Esto significa que no tiene sentido voltear ninguno de estos tipos de cartas. Supongamos que sí volteo una tarjeta con un número impar. ¿Importa qué hay del otro lado? No, porque nuestra hipótesis no hace ninguna predicción al respecto. No importa lo que esté del otro lado, es compatible con la hipótesis.
Pero ¿qué pasa con las tarjetas que tienen números pares en ellas? Esos son los que se encuentran fuera del círculo grande en la Figura 27.2.3, fuera en zonas como las ocupadas por las tres estrellas (***). Podemos ver que las tarjetas aquí afuera no pueden ser vocales. Entonces, necesitamos voltear tarjetas aquí (que todas tienen números pares boca arriba). Si una carta de aquí afuera tiene una vocal, la hipótesis que estamos probando es falsa.
También podemos utilizar el diagrama para explicar la respuesta en términos de condiciones necesarias y suficientes. La hipótesis dice que tener una vocal en un lado es suficiente para tener un número impar en el otro. Entonces, necesitamos voltear cada tarjeta vocal, y si encontramos una par sin un número impar del otro lado, la afirmación es falsa. De igual manera, la hipótesis dice que tener un número impar en un lado es una condición necesaria para tener una vocal en el otro. Entonces, si encontramos solo una carta par con una vocal en el otro lado, la afirmación es falsa. Podemos ver en nuestro cuadro que la hipótesis requiere que si una carta no es impar (= par), entonces no es una vocal. Si encontramos una carta, digamos ***, eso no es extraño sino que es una vocal, la hipótesis es falsa. El patrón argumental relevante aquí es negar lo consecuente.
Hay alguna evidencia de que las personas son mejores en problemas como este cuando involucran reglas y obligaciones. Nos va mucho mejor si nos pregunta qué personas debe revisar un policía para ver si todos están obedeciendo la regla:
- Regla: Si compras cerveza, debes tener al menos veintiún años.
¿Cuál es la respuesta? ¿Por qué podríamos hacerlo mejor con problemas como este?
Validez de la imagen
.png)
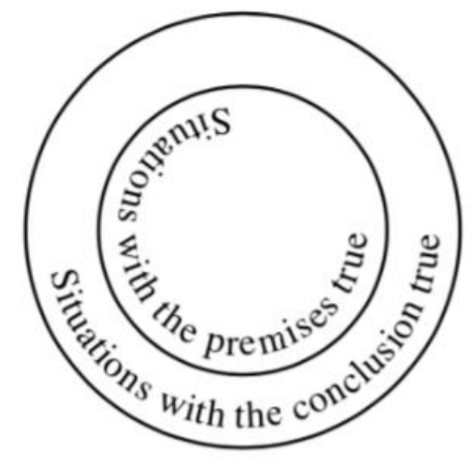
Un argumento es válido por si acaso es imposible que todas sus premisas sean ciertas mientras que su conclusión es falsa. Esto significa que no hay manera de que todas las premisas puedan ser verdaderas y la conclusión falsa. Entonces, en toda situación posible en la que todas las premisas sean verdaderas, la conclusión también debe ser cierta.
Podemos dibujar una imagen de esto representando el conjunto de todas las situaciones posibles en las que las premisas son verdaderas por el círculo interior, más pequeño en la Figura 27.2.5 de la página anterior y el conjunto de todas las situaciones en las que la conclusión es verdadera por el círculo más grande, exterior.
Por el contrario, si un argumento es inválido, existe algún escenario posible en el que las premisas son verdaderas y la conclusión es falsa. Por supuesto, la definición de validez permite que la conclusión sea cierta en situaciones adicionales en las que una o más premisas son falsas.


