33.3: Reclamaciones múltiples

Cuando tenemos más de una afirmación, podemos usar tablas de verdad para compararlas, y al hacerlo determinar relaciones más complicadas.

Consistencia

La primera relación que probaremos es la consistencia. La consistencia es una relación bastante simple. Significa que las afirmaciones pueden ser ciertas al mismo tiempo. Al igual que con la tautología, contradicción y contingencia a veces será obvio que dos afirmaciones son consistentes. Las reclamaciones no relacionadas siempre van a ser consistentes, por ejemplo. A Troya le gustan las manzanas y Godzilla es el rey de los monstruos son consistentes porque no tienen nada que ver entre sí, y no necesitamos una mesa para probarlo. Aún así, habrá momentos en los que las reclamaciones sean complejas (o cuando se quiera comparar una gran cantidad de reclamaciones) y las tablas pueden ser muy útiles en esos casos. En aras de la simplicidad, nos centraremos en pares de oraciones complejas, pero no hay límite en el número de afirmaciones que podrías probar para verificar la consistencia al mismo tiempo.

En cuanto a cómo deberían verse las tablas, dos afirmaciones son consistentes si hay alguna fila en la que ambas afirmaciones sean veraces al mismo tiempo. Veamos la tabla comparando 'P v Q' y 'P & Q'.

Ambas afirmaciones son ciertas en la fila 1, por lo que estas afirmaciones son consistentes.

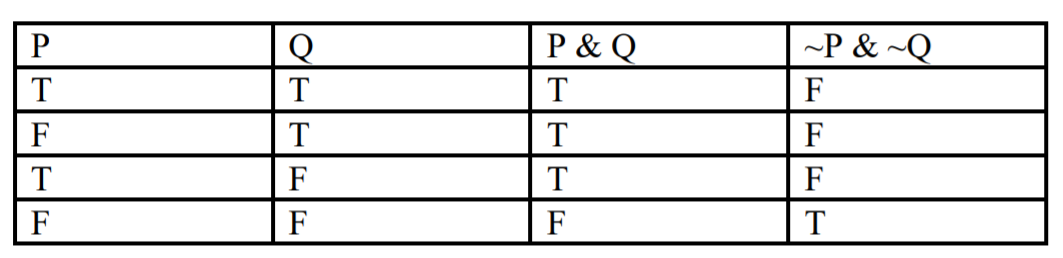
Ahora veamos un ejemplo donde las afirmaciones no son consistentes. A continuación se muestra la tabla que divide 'P & Q' y '~P & ~Q'.

Observe que no hay línea donde ambas reclamaciones sean veraces, por lo que las reclamaciones no son consistentes. Cuando las afirmaciones no son consistentes, decimos que son inconsistentes, y para reiterar, esto significa que ambas no pueden ser ciertas al mismo tiempo.

Equivalencia

También podemos usar tablas para comparar sentencias para determinar si son lógicamente equivalentes. Cuando las reclamaciones son lógicamente equivalentes, ambas contienen la misma información. Se puede pensar en ello como las dos declaraciones que dicen lo mismo (aunque no se vean como lo hacen). Para probar la equivalencia, hacemos una tabla de la verdad y nuevamente le ponemos ambas afirmaciones. Si las declaraciones tienen el mismo valor de verdad en todas las líneas, entonces son lógicamente equivalentes. La siguiente tabla de verdad muestra que '~ (P v Q) 'y '~P & ~Q' son lógicamente equivalentes:

La siguiente tabla de verdad muestra que 'P v Q' y 'P & Q' no son lógicamente equivalentes, porque los resultados en la tabla difieren en las filas 2 y 3.

Ejercicios

Construir tablas de verdad para los siguientes conjuntos de sentencias para probar la consistencia y equivalencia lógica.

1. P v ~Q; P → Q
2. ~ (P v ~P); P y ~P
3. ~ (Q v P) → P; ~Q
4. P v [P & (Q → R)]; P v (Q v R)
5. (P → Q) y (Q → P); P ← → Q
6. P v ~P; P v Q
7. P ← → (Q ← → R); P ← → R
8. P← →Q; Q← → P
9. ~ (P v ~Q); P → Q
10. P v ~ (P ← → Q); (P & ~Q) v (~P & Q)
11. P → Q; Q → P
12. P → Q; ~ (Q → P)
13. ~ (P ← → Q); (~P & Q) v (P & ~Q)
14. ~ (~P v ~~Q); P & ~Q
15. P ← → (Q → ~R); ~P v ~Q
16. P v (Q v R); (P v Q) v R
17. P & (Q & R); (P & R) & Q
18. P & (Q v R); (P & Q) v R
19. P & (Q v R); (Q v R) & P
20. ~ (P → Q) v [P v (~Q → P)]; (P ← → Q) v [(P v ~P) & (Q v ~Q)]

Respuestas Seleccionadas

1. P v ~Q; P → Q

Estas afirmaciones son consistentes ya que coinciden en las filas 1 y 4, pero no son equivalentes ya que no están de acuerdo en las líneas 2 y 3.

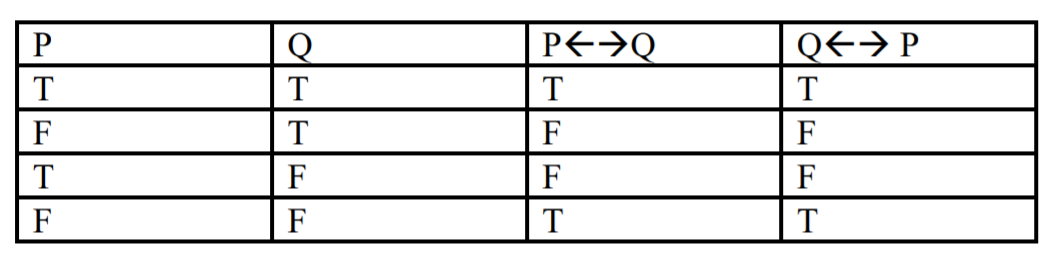
8. P← →Q; Q← → P

Estas afirmaciones son equivalentes ya que coinciden en todas las filas. Todas las reclamaciones equivalentes son consistentes por lo que también son consistentes.

14. ~ (~P v ~~Q); P & ~Q

Antes incluso de hacer una tabla en este caso podemos usar las reglas de manipulación de negación para hacernos las cosas más simples. '~ (~P v ~~Q) 'se convierte en 'P & ~Q'. Ahora podríamos hacer una mesa, pero convertimos el primer reclamo en exactamente lo mismo que el segundo, así sabemos que son equivalentes.