3.1.3: Ecuación de cantidad de movimiento

La ecuación de cantidad de movimiento en un fluido (también conocida como ecuación de impulso) es la segunda expresión de la ley de Newton aplicada a un fluido:

\[\sum \vec{F} = m \dfrac{d(\vec{V})}{dt}.\]

Las fuerzas ejercidas sobre la materia, sólida o fluida, pueden ser de dos tipos:

• Distancia-ejercida, e.g., gravitacional, eléctrica, magnética; relacionada con la masa o el volumen.
• Contacto ejercido, e.. g, presión o fricción, relacionado con la superficie de contacto.

Ecuación de Euler

Asumimos aquí que el fluido es inviscoso y, por lo tanto, no consideramos las fuerzas de fricción. Las únicas fuentes de fuerzas son la presión y la gravedad. Consideramos el flujo unidimensional a lo largo del eje longitudinal.

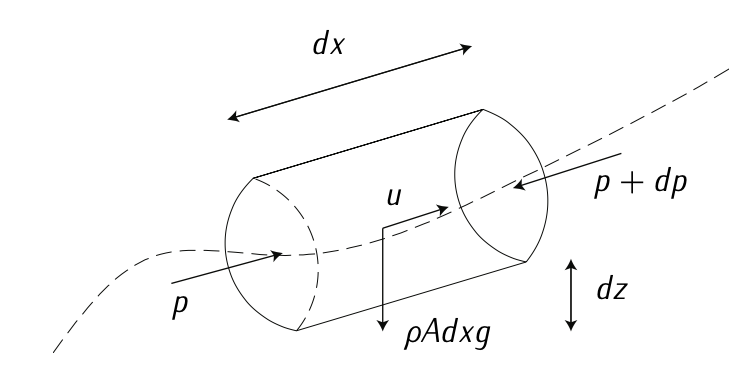
Figura 3.4: Cantidad de movimiento. Adaptado de\(F_{\text{RANCHINI}}\) et al. [4].

Supongamos que hay una partícula fluida con sección circular\(A\) y longitud que\(dx\) se mueve con velocidad\(u\) en dirección\(x\). Aplicar segunda ley Newton (\(m \dot{u} = \sum F\);\(m = \rho Adx\)):

\[(\rho A dx) \dfrac{du}{dt} = -Adp - (\rho A dx) g \dfrac{dz}{dx}.\label{eq3.1.3.2}\]

La fuerza debida a la gravedad sólo afecta en la dirección del eje\(x\).

Considerando un marco de referencia unido a la partícula en la que\(dt = \dfrac{dx}{u}\) (flujo estacionario), la aceleración se puede escribir como\(\tfrac{du}{dt} = \dfrac{du}{dx/u}\) y Ecuación (\(\ref{eq3.1.3.2}\)), dividiendo por\(Adx\). rinde:

\[\rho u \dfrac{du}{dx} = - \dfrac{dp}{dx} - \rho g \dfrac{dz}{dx}.\label{eq3.1.3.3}\]

La ecuación (\(\ref{eq3.1.3.3}\)) se conoce como ecuación de Euler. Este es el caso unidimensional. La ecuación de Euler es más compleja, considerando el movimiento tridimensional. La ecuación completa se verá es cursos posteriores de mecánica de fluidos.

Ecuación de Bernoulli

Considere la Ecuación (\(\ref{eq3.1.3.3}\)) y observe que la partícula se mueve en la dirección de la línea aerodinámica. Si el flujo es incompresible (o existe una relación entre presión y densidad, relación llamada barotropía), la ecuación se puede integrar a lo largo de la línea aerodinámica:

\[\rho \dfrac{u^2}{2} + p + \rho gz = C.\label{eq3.1.3.4}\]

El valor de la constante de integración,\(C\), debe calcularse con las condiciones conocidas de un punto. La ecuación de Bernouilli expresa que la suma de la presión dinámica (\(\rho \tfrac{u^2}{2}\)), la presión estática (\(p\)) y la presión piezométrica (\(\rho g z\)) es constante a lo largo de un tubo de corriente.

En el caso del aire que se mueve alrededor de un avión, el término\(\rho g z\) no varía significativamente entre los diferentes puntos de la aerodinámica y se puede descuidar. La ecuación (\(\ref{eq3.1.3.4}\)) se simplifica a continuación para:

\[\rho \dfrac{u^2}{2} + p = C.\]

Esto no ocurre en líquidos, donde la densidad es de un orden de miles mayor que en gases y el término piezométrico siempre es tan importante como el resto de términos (salvo si el movimiento es horizontal).

Si en algún punto de la línea aerodinámica la velocidad es nula, el punto se denominará punto de estancamiento. En ese punto, la presión toma un valor conocido como presión de estancamiento (\(p_T\)), de manera que en cualquier otro punto sostiene:

\[u = \sqrt{2 \dfrac{p_T - p}{\rho}}.\]