2.4: Señales de Tiempo Discreto
- Page ID
- 85591
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Las señales se pueden representar por cantidades discretas en lugar de como una función de una variable continua.
- Estas señales de tiempo discretas no necesariamente tienen que tomar valores de números reales.
- Muchas propiedades de las señales de valor continuo se transfieren casi directamente al dominio discreto.
Hasta el momento, hemos tratado lo que se conoce como señales y sistemas analógicos. Matemáticamente, las señales analógicas son funciones que tienen cantidades continuas como sus variables independientes, como el espacio y el tiempo. Las señales de tiempo discreto son funciones definidas en los números enteros; son secuencias. Uno de los resultados fundamentales de la teoría de la señal detallará las condiciones bajo las cuales una señal analógica puede convertirse en una de tiempo discreto y recuperarse sin error. Este resultado es importante porque las señales de tiempo discreto pueden ser manipuladas por sistemas instanciados como programas informáticos. Los módulos posteriores describen cómo prácticamente todo el procesamiento de señales analógicas se puede realizar con software.
Por importantes que sean tales resultados, las señales de tiempo discreto son más generales, abarcando señales derivadas de señales analógicas y señales que no lo son. Por ejemplo, los caracteres que forman un archivo de texto forman una secuencia, que también es una señal de tiempo discreto. También debemos tratar con tales señales y sistemas de valor simbólico.
Al igual que con las señales analógicas, buscamos formas de descomponer señales de tiempo discreto de valor real en componentes más simples. Con este enfoque que conduce a una mejor comprensión de la estructura de la señal, podemos explotar esa estructura para representar información (crear formas de representar información con señales) y para extraer información (recuperar la información así representada). Para las señales de valor simbólico, el enfoque es diferente: Desarrollamos una representación común de todas las señales de valor simbólico para que podamos encarnar la información que contienen de manera unificada. Desde una perspectiva de representación de la información, el tema más importante se convierte, tanto para señales de valor real como simbólico, en eficiencia; cuál es la forma más parsimoniosa y compacta de representar la información para que pueda extraerse posteriormente.
Señales de valor real y complejo
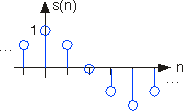
Una señal de tiempo discreto se representa simbólicamente como s (n), donde n = {..., -1,0,1...}. Por lo general, dibujamos señales de tiempo discreto como diagramas madre para enfatizar el hecho de que son funciones definidas solo en los enteros. Podemos retrasar una señal de tiempo discreto en un entero igual que con las analógicas. Una muestra unitaria retardada tiene la expresión
δ (n − m ) δ (n − m )\[\delta (n-m) \nonumber \]
y es igual a uno cuando n = m.
Exponenciales Complejos
La señal más importante es, por supuesto, la compleja secuencia exponencial.
\[s(n) = e^{i2\pi fn} \nonumber \]
Sinusoides
Las sinusoides de tiempo discreto tienen la forma obvia
\[s(n) = A\cos (2\pi fn+\varphi ) \nonumber \]
A diferencia de exponenciales complejos analógicos y sinusoides que pueden tener sus frecuencias de cualquier valor real, las frecuencias de sus contrapartes de tiempo discreto producen formas de onda únicas solo cuando f se encuentra en el intervalo (-½,½). Esta propiedad se puede entender fácilmente al señalar que agregar un entero a la frecuencia del complejo exponencial discreto en el tiempo no tiene ningún efecto sobre el valor de la señal.
\[e^{i2\pi (f+m)n} = e^{i2\pi fn}e^{i2\pi mn}\\ e^{i2\pi (f+m)n} = e^{i2\pi fn} \nonumber \]
Esta derivación sigue porque el complejo exponencial evaluado en un múltiplo entero de 2π es igual a uno.
Muestra de Unidad
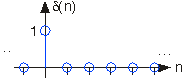
La segunda señal de tiempo discreto más importante es la muestra unitaria, que se define como
\[\delta (n) = 1\; if\; n=0\\ \delta (n) = 0\; otherwise \nonumber \]
El examen de la gráfica de una señal de tiempo discreto, como la de la señal coseno mostrada en la Figura 2.4.1, revela que todas las señales consisten en una secuencia de muestras unitarias retardadas y escaladas. Porque el valor de una secuencia en cada entero m se denota por s (m) y se escribe la muestra unitaria retardada para ocurrir en m
δ (n − m )\[\delta (n-m) \nonumber \]
podemos descomponer cualquier señal como una suma de muestras unitarias retrasadas a la ubicación apropiada y escaladas por el valor de la señal.
\[s(n) = \sum_{m=-\infty }^{\infty }s(m)\delta (n-m) \nonumber \]
Este tipo de descomposición es exclusivo de las señales de tiempo discreto, y resultará útil posteriormente.
Los sistemas de tiempo discreto pueden actuar sobre señales de tiempo discreto de maneras similares a las que se encuentran en señales y sistemas analógicos. Debido al papel del software en los sistemas de tiempo discreto, se pueden imaginar y “construir” muchos más sistemas diferentes con programas que con señales analógicas. De hecho, una clase especial de señales analógicas se puede convertir en señales de tiempo discreto, procesarse con software y volver a convertirse en una señal analógica, todo sin incursión de error. Para tales señales, los sistemas se pueden producir fácilmente en software, con realizaciones analógicas equivalentes difíciles, si no imposibles, de diseñar.
Señales de valor simbólico
Otro aspecto interesante de las señales de tiempo discreto es que sus valores no necesitan ser números reales. Tenemos señales de tiempo discreto de valor real como la sinusoide, pero también tenemos señales que denotan la secuencia de caracteres escritos en el teclado. Tales personajes ciertamente no son números reales, y como colección de posibles valores de señal, tienen poca estructura matemática aparte de que son miembros de un conjunto. De manera más formal, cada elemento de la señal de valor simbólico s (n) adquiere uno de los valores {a 1,... a K} que comprenden el alfabeto A. Esta terminología técnica no significa que restrinjamos símbolos a ser miembros del alfabeto inglés o griego. Podrían representar caracteres de teclado, bytes (cantidades de 8 bits), enteros que transmiten la temperatura diaria. Ya sea controlado por software o no, los sistemas de tiempo discreto se construyen en última instancia a partir de circuitos digitales, que consisten completamente en elementos de circuitos analógicos. Además, la transmisión y recepción de señales de tiempo discreto, como el correo electrónico, se logra con señales y sistemas analógicos. Comprender cómo el tiempo discreto y las señales analógicas y los sistemas se entrelazan es quizás el objetivo principal de este curso.


