2.5: Introducción a los sistemas

Objetivos de aprendizaje

• Introducción al concepto de un sistema, que es un mecanismo de manipulación de señales.
• También se mencionan brevemente los conceptos de retroalimentación y las superposiciones.

Las señales son manipuladas por los sistemas. Matemáticamente, representamos lo que hace un sistema por la notación

\[y(t) = S\left ( x(t) \right ) \nonumber \]

con x representando la señal de entrada e y la señal de salida.

Figura 2.5.1 El sistema representado tiene entrada x (t) y salida y (t). Matemáticamente, los sistemas operan en función (s) para producir otra (s) función (s). En muchos sentidos, los sistemas son como funciones, reglas que producen un valor para la variable dependiente (nuestra señal de salida) para cada valor de su variable independiente (su señal de entrada). La notación y (t) =S (x (t)) corresponde a este diagrama de bloques. Se denomina S (•) la relación entrada-salida para el sistema.

Esta notación imita la simbología matemática de una función: La entrada de un sistema es análoga a una variable independiente y su salida es la variable dependiente. Para los matemáticamente inclinados, un sistema es un funcional: una función de una función (las señales son funciones).

Los sistemas simples se pueden conectar entre sí (la salida de un sistema se convierte en la entrada de otro) para lograr cierto diseño general. Las topologías de interconexión pueden ser bastante complicadas, pero generalmente consisten en tejidos de tres formas básicas de interconexión.

Interconexión en cascada

Figura 2.5.2 Las formas más rudimentarias de interconectar sistemas se muestran en las figuras de esta sección. Esta es la configuración en cascada.

La forma más simple es cuando la salida de un sistema está conectada solo a la entrada de otro. Matemáticamente,

\[w(t) = S_{1}\left ( x(t) \right )\\ y(t) = S_{2}\left ( x(t) \right ) \nonumber \]

con la información contenida en x (t) procesada por el primero, luego el segundo sistema. En algunos casos, el ordenamiento de los sistemas importa, en otros no. Por ejemplo, en el modelo fundamental de comunicación el ordenamiento ciertamente importa.

Interconexión Paralelo

Figura 2.5.3 La configuración paralela

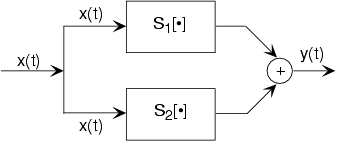
Una señal x (t) se enruta a dos (o más) sistemas, apareciendo esta señal como entrada a todos los sistemas simultáneamente y con igual intensidad. Los diagramas de bloques tienen la convención de que las señales que van a más de un sistema no se dividen en pedazos a lo largo del camino. Dos o más sistemas operan en x (t) y sus salidas se suman para crear la salida y (t). Por lo tanto,

\[y(t) = S_{1}\left ( x(t) \right )+ S_{2}\left ( x(t) \right ) \nonumber \]

La información en x (t) es procesada por separado por ambos sistemas.

Interconexión de retroalimentación

Figura 2.5.4 La configuración de retroalimentación

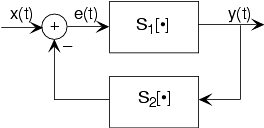
La configuración de interconexión más sutil tiene la salida de un sistema que también contribuye a su entrada. Los ingenieros dirían que la salida es “retroalimentada” a la entrada a través del sistema 2, de ahí la terminología. La declaración matemática de la interconexión de retroalimentación es que el sistema feed-forward produce la salida:

\[y(t) = S_{1}\left ( e(t) \right ) \nonumber \]

La entrada e (t) es igual a la señal de entrada menos la salida de algún otro sistema para:

\[y(t):e(t) = x(t)- S_{2}\left ( y(t) \right ) \nonumber \]

Los sistemas de retroalimentación son omnipresentes en los problemas de control, con la señal de error utilizada para ajustar la salida para lograr alguna condición definida por la señal de entrada (controladora). Por ejemplo, en el sistema de control de crucero de un automóvil, x (t) es una constante que representa la velocidad que desea, e y (t) es la velocidad del automóvil medida por un velocímetro. En esta aplicación, el sistema 2 es el sistema de identidad (salida es igual a entrada).