3.6: Circuitos en serie y paralelos
- Page ID
- 85479
- Una breve mirada a los circuitos en serie y paralelos. También define divisor de voltaje y corriente.
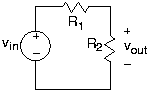
Los resultados mostrados en otros módulos (elementos de circuito, KVL y KCL, leyes de interconexión) con respecto al circuito anterior y los valores de otras corrientes y voltajes en este circuito también, tienen profundas implicaciones.
Se dice que las resistencias conectadas de tal manera que la corriente de uno solo debe fluir hacia otra, las corrientes en todas las resistencias conectadas de esta manera tienen la misma magnitud, están conectadas en serie. Para las dos resistencias conectadas en serie en el ejemplo, el voltaje a través de una resistencia es igual a la relación del valor de esa resistencia y la suma de resistencias por el voltaje a través de la combinación en serie. Este concepto es tan penetrante que tiene un nombre: divisor de voltaje.
La relación entrada-salida para este sistema, encontrada en este caso particular por divisor de voltaje, toma la forma de una relación entre la tensión de salida y la tensión de entrada.
\[\frac{v_{out}}{v_{in}} = \frac{R_{2}}{R_{1}+R_{2}} \nonumber \]
De esta manera, expresamos cómo los componentes utilizados para construir el sistema afectan la relación input-output. Debido a que este análisis se realizó con elementos de circuito ideales, podríamos esperar que esta relación se rompa si la amplitud de entrada es demasiado alta (¿Sobrevivirá el circuito si la entrada cambia de 1 voltio a un millón de voltios?) o si la frecuencia de la fuente se vuelve demasiado alta. En cualquier caso, esta importante forma de expresar las relaciones entrada-salida, como una relación entre salida y entrada, invade la teoría de circuitos y sistemas.
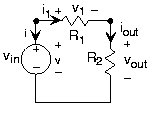
La corriente i 1 es la corriente que fluye fuera de la fuente de voltaje. Porque es igual a i 2, tenemos que
\[\frac{v_{in}}{i_{1}} = R_{1}+R_{2} \nonumber \]
La combinación en serie de dos resistencias actúa, en lo que a la fuente de voltaje se refiere, como una sola resistencia que tiene un valor igual a la suma de las dos resistencias.
Este resultado es el primero de varias ideas de servicio equivalentes: En muchos casos, un circuito complicado cuando se ve desde sus terminales (los dos lugares a los que podría adjuntar una fuente) parece ser un solo elemento de circuito (en el mejor de los casos) o una simple combinación de elementos en el peor de los casos. Así, el circuito equivalente para una combinación en serie de resistencias es una sola resistencia que tiene una resistencia igual a la suma de sus resistencias componentes.
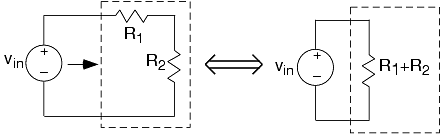
Así, el circuito que la fuente de voltaje “siente” (a través de la corriente extraída de ella) es una sola resistencia que tiene resistencia R 1 +R2. Tenga en cuenta que al hacer este circuito equivalente, ya no se puede definir el voltaje de salida: La resistencia de salida etiquetada como R2 ya no aparece. Así, esta equivalencia se hace estrictamente desde el punto de vista de la fuente de voltaje.
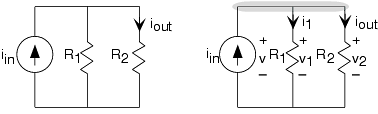
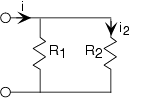
Un circuito sencillo interesante en la Figura 3.6.3 tiene dos resistencias conectadas lado a lado, lo que denominaremos una conexión paralela, en lugar de en serie. Aquí, aplicando KVL revela que todos los voltajes son idénticos: v 1 =v y v 2 = v. Este resultado tipifica las conexiones paralelas. Para escribir la ecuación KCL, tenga en cuenta que el nodo superior consiste en toda la sección de interconexión superior. La ecuación de KCL es:
\[i_{in}-i_{1}-i_{2}=0 \nonumber \]
Usando las relaciones v-i, encontramos que
\[i_{out} = \frac{R_{1}}{R_{1}+R_{2}}i_{in} \nonumber \]
Supongamos que reemplazó la fuente de corriente en la Figura 3.6.3 por una fuente de voltaje. ¿Cómo estaría relacionado con el voltaje de la fuente? Con base en este resultado, ¿qué propósito tiene este circuito revisado?
Solución
Reemplazar la fuente de corriente por una fuente de voltaje no cambia el hecho de que los voltajes son idénticos. En consecuencia,
\[v_{in}=R_{2}i_{out}\; \; or\; \; i_{out}=\frac{v_{in}}{R_{2}} \nonumber \]
Este resultado no depende de la resistencia R1, lo que significa que simplemente tenemos una resistencia (R2) a través de una fuente de voltaje. El circuito de dos resistencias no tiene un uso aparente.
Este circuito destaca algunas propiedades importantes de los circuitos paralelos. Puede demostrar fácilmente que la combinación paralela de R1 y R2 tiene la relación v-i de una resistencia que tiene resistencia:
\[\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}} \right )^{-1}=\frac{R_{1}R_{2}}{R_{1}+R_{2}} \nonumber \]
Una notación taquigráfica para esta cantidad es
\[R_{1}\parallel R_{2} \nonumber \]
Como el recíproco de la resistencia es la conductancia, podemos decir que para una combinación paralela de resistencias, la conductancia equivalente es la suma de las conductancias.
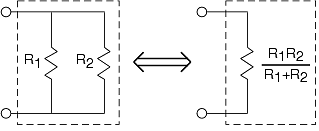
Similar al divisor de voltaje en la figura 3.6.1 para resistencias en serie, tenemos divisor de corriente para resistencias paralelas. La corriente a través de una resistencia en paralelo con otra es la relación de la conductancia de la primera a la suma de las conductancias. Así, para el circuito representado,
\[i_{2}=\frac{G_{2}}{G_{1}+G_{2}}i \nonumber \]
Expresado en términos de resistencias, el divisor de corriente toma la forma de la resistencia de la otra resistencia dividida por la suma de resistencias:
\[i_{2}=\frac{R_{1}}{R_{1}+R_{2}}i \nonumber \]
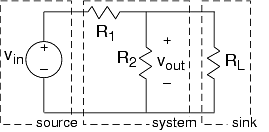
\[v_{out}=\frac{R_{2}}{R_{1}+R_{2}}v_{in} \nonumber \]
Supongamos que queremos pasar la señal de salida a un dispositivo de medición de voltaje, como un osciloscopio o un voltímetro. En términos de teoría de sistemas, queremos pasar la salida de nuestro circuito a un sumidero. Para la mayoría de las aplicaciones, podemos representar estos dispositivos de medición como una resistencia, con la corriente que pasa a través de él impulsando el dispositivo de medición a través de algún tipo de pantalla. En los circuitos, un sumidero se llama carga; así, describimos un sumidero teórico del sistema como una resistencia de carga R L. Así, tenemos un sistema completo construido a partir de una cascada de tres sistemas: una fuente, un sistema de procesamiento de señal (simple como es) y un sumidero.
Debemos analizar de nuevo cómo funciona este circuito revisado, mostrado en la Figura 3.6.5. En lugar de definir ocho variables y resolver la corriente en la resistencia de carga, tomemos una pista de otros análisis (reglas de serie, reglas paralelas). Las resistencias R2 y R L están en una configuración paralela: Los voltajes a través de cada resistor son los mismos mientras que las corrientes no lo son. Debido a que los voltajes son los mismos, podemos encontrar la corriente a través de cada uno a partir de sus relaciones v-i:
\[i_{2}=\frac{v_{out}}{R_{2}}\; \: and\; \; i_{L}=\frac{v_{out}}{R_{L}} \nonumber \]
Considerando el nodo donde se unen las tres resistencias, KCL dice que la suma de las tres corrientes debe ser igual a cero. Dicho de otra manera, la corriente que ingresa al nodo a través de R1 debe ser igual a la suma de las otras dos corrientes que salen del nodo. Por lo tanto,
\[i_{1}=i_{2}+i_{L}\\ i_{1}=v_{out}\left ( \frac{1}{R_{2}}+\frac{1}{R_{L}} \right ) \nonumber \]
Sea R eq denota la resistencia equivalente de la combinación paralela de R2 y RL. Usando la relación v-i de R 1, el voltaje a través de ella es
\[v_{1}=\frac{R_{1}v_{out}}{R_{eq}} \nonumber \]
La ecuación KVL escrita alrededor del bucle más a la izquierda tiene
\[v_{in}=v_{1}+v_{out} \nonumber \]
Sustituyendo por v 1, encontramos
\[v_{in}=v_{out}\left ( \frac{R_{1}}{R_{eq}} +1\right ) \nonumber \]
\[\frac{v_{out}}{v_{in}}=\frac{R_{1}}{R_{eq}} +1 \nonumber \]
Así, tenemos la relación entrada-salida para todo nuestro sistema teniendo la forma de divisor de voltaje, pero no iguala la relación entrada-salida del circuito sin el dispositivo de medición de voltaje. No podemos medir voltajes de manera confiable a menos que el dispositivo de medición tenga poco efecto en lo que estamos tratando de medir. Deberíamos mirar más cuidadosamente para determinar si algún valor para la resistencia de carga disminuiría su impacto en el circuito. Comparando las relaciones insumo-producto antes y después, lo que necesitamos es
\[R_{eq}\approx R_{2} \nonumber \]
Como
\[R_{eq}=\left ( \frac{1}{R_{2}}+\frac{1}{R_{L}} \right )^{-1} \nonumber \]
La aproximación se aplicaría si
\[\frac{1}{R_{2}}\gg \frac{1}{R_{L}}\; \; or\\ R_{2}\ll R_{L} \nonumber \]
Esta es la condición que buscamos:
Los dispositivos de medición de voltaje deben tener grandes resistencias en comparación con la resistencia a través de la cual se va a medir el voltaje.
Seamos más precisos: ¿Cuánto mayor tendría que ser una resistencia de carga para afectar la relación entrada-salida en menos del 10%? en menos del 1%?
Solución
\[R_{eq}=\frac{R_{2}}{1+\frac{R_{2}}{R_{L}}} \nonumber \]
Así, un cambio del 10% significa que la relación
\[\frac{R_{2}}{R_{L}}< 0.1 \nonumber \]
Un cambio de 1% significa que
\[\frac{R_{2}}{R_{L}}< 0.01 \nonumber \]
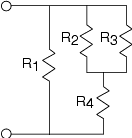
Queremos encontrar la resistencia total del circuito de ejemplo. Para aplicar las reglas de combinación en serie y paralelo, lo mejor es determinar primero la estructura del circuito: Qué hay en serie con qué y qué es en paralelo con qué en vistas tanto a pequeña como a gran escala. Tenemos R 2 en paralelo con R 3; esta combinación está en serie con R 4. Esta combinación de series está en paralelo con R 1. Tenga en cuenta que al determinar esta estructura, partimos de las terminales, y trabajamos hacia ellas. En la mayoría de los casos, este enfoque funciona bien; pruébalo primero. La expresión de resistencia total imita la estructura:
\[R_{T}=R_{1}\parallel (R_{2}\parallel R_{3}+R_{4})\\ R_{T}=\frac{R_{1}R_{2}R_{3}+R_{1}R_{2}R_{4}+R_{1}R_{3}R_{4}}{R_{1}R_{2}+R_{2}R_{3}+R_{2}R_{4}+R_{3}R_{4}} \nonumber \]
Tales expresiones complicadas tipifican circuito “simplificaciones”. Una simple comprobación de precisión son las unidades: Cada componente del numerador debe tener las mismas unidades (aquí Ω 3) así como en el denominador (Ω 2). Toda la expresión es tener unidades de resistencia; así, la relación de las unidades del numerador y del denominador debe ser ohmios. La comprobación de las unidades no garantiza la precisión, pero puede detectar muchos errores.
Otra valiosa lección surge de este ejemplo sobre la diferencia entre sistemas en cascada y circuitos en cascada. En la teoría de sistemas, los sistemas pueden ser conectados en cascada sin cambiar la relación entrada-salida de los sistemas intermedios. En los circuitos en cascada, este ideal rara vez es cierto a menos que los circuitos estén así diseñados. El diseño está en manos del ingeniero; él o ella debe reconocer lo que se ha llegado a conocer como efectos de carga. En nuestro sencillo circuito, se podría pensar que hacer la resistencia R L lo suficientemente grande serviría el truco. Debido a que las resistencias R1 y R2 pueden tener prácticamente cualquier valor, nunca podrá hacer que la resistencia de su dispositivo de medición de voltaje sea lo suficientemente grande. Dicho de otra manera, no se puede diseñar un circuito aislado que funcione en cascada con todos los demás circuitos. Los ingenieros eléctricos atienden esta situación a través de la noción de especificaciones: ¿En qué condiciones funcionará el circuito según lo diseñado? Así, encontrarás que los osciloscopios y voltímetros tienen sus resistencias internas claramente establecidas, lo que te permite determinar si el voltaje que mides es muy similar a lo que estaba presente antes de que fueran conectados a tu circuito. Además, dado que nuestro circuito de resistencia funciona como un atenuador, con la atenuación (una palabra elegante para ganancias menores de uno) dependiendo solo de la relación de los dos valores de resistencia:
\[\frac{R_{2}}{R_{1}+R_{2}}=\left ( 1+\frac{R_{1}}{R_{2}} \right )^{-1} \nonumber \]
Podemos seleccionar cualquier valor para las dos resistencias que queramos para lograr la atenuación deseada. Por lo tanto, el diseñador de este circuito debe especificar no solo cuál es la atenuación, sino también los valores de resistencia empleados para que los integradores —personas que juntan sistemas a partir de sistemas componentes— puedan combinar sistemas y tener la oportunidad de que la combinación funcione.
La Figura 3.6.6 a continuación, resume los resultados de la combinación de series y paralelas. Estos resultados son fáciles de recordar y muy útiles. Tenga en cuenta que para las combinaciones en serie, el voltaje y la resistencia son las cantidades clave, mientras que para las combinaciones paralelas la corriente y la conductancia son más importantes. En combinaciones en serie, las corrientes a través de cada elemento son las mismas; en las paralelas, las tensiones son las mismas.
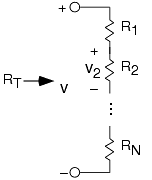
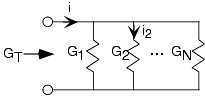
Contraste una combinación en serie de resistencias con una paralela. ¿Qué variable (voltaje o corriente) es la misma para cada una y cuál difiere? ¿Cuáles son las resistencias equivalentes? Cuando las resistencias se colocan en serie, ¿la resistencia equivalente es mayor, intermedia o menor que las resistencias de los componentes? ¿Cuál es esta relación para una combinación paralela?
Solución
En una combinación en serie de resistencias, la corriente es la misma en cada una; en una combinación paralela, la tensión es la misma. Para una combinación en serie, la resistencia equivalente es la suma de las resistencias, que será mayor que el valor de cualquier resistencia componente; para una combinación paralela, la conductancia equivalente es la suma de las conductancias de los componentes, que es mayor que cualquier conductancia de componente. Por lo tanto, la resistencia equivalente es menor que la resistencia de cualquier componente.