3.13: Funciones de transferencia
- Page ID
- 85458
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Introducción de la función de transferencia (respuesta de frecuencia).

La relación de las amplitudes de salida y entrada para la Figura 3.13.1, conocida como función de transferencia o respuesta de frecuencia, viene dada por
\[\frac{V_{out}}{V_{in}}=H(f) \nonumber \]
\[\frac{V_{out}}{V_{in}}=\frac{1}{i2\pi fRC+1} \nonumber \]
Implícito en el uso de la función de transferencia es que la entrada es un exponencial complejo, y la salida también es un exponencial complejo que tiene la misma frecuencia. La función de transferencia revela cómo el circuito modifica la amplitud de entrada al crear la amplitud de salida. Así, la función de transferencia describe completamente cómo el circuito procesa el complejo de entrada exponencial para producir el complejo de salida exponencial. La función del circuito es así resumida por la función de transferencia. De hecho, los circuitos suelen estar diseñados para cumplir con las especificaciones de la función de transferencia. Debido a que las funciones de transferencia son cantidades de valor complejo y dependen de la frecuencia, podemos apreciar mejor la función de un circuito examinando la magnitud y fase de su función de transferencia (Ver Figura 3.13.2 a continuación)
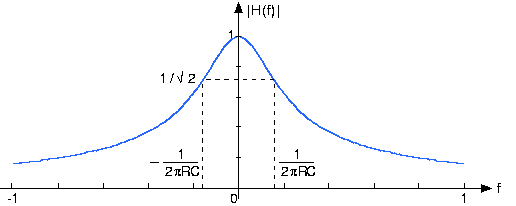
\[\left | H(f) \right |=\frac{1}{\sqrt{(2\pi fRC)^{2}+1}} \nonumber \]
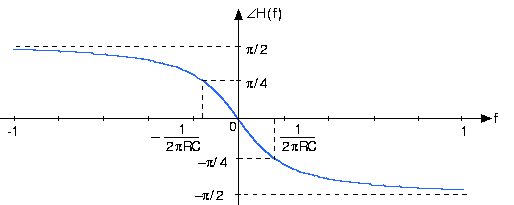
\[\angle (H(f))=-\arctan (2\pi fRC) \nonumber \]
Figura 3.13.2 Magnitud y fase de la función de transferencia del circuito RC cuando RC=1
Esta función de transferencia tiene muchas propiedades importantes y proporciona todos los conocimientos necesarios para determinar cómo funciona el circuito. En primer lugar, tenga en cuenta que podemos calcular la respuesta de frecuencia tanto para frecuencias positivas como negativas. Recordemos que los sinusoides consisten en la suma de dos exponenciales complejos, uno teniendo la frecuencia negativa del otro. Consideraremos cómo actúa el circuito sobre una sinusoide pronto. Tenga en cuenta que la magnitud tiene simetría par: La porción de frecuencia negativa es una imagen especular de la porción de frecuencia positiva:
\[\left | H(-f) \right |=\left | H(f) \right | \nonumber \]
La fase tiene simetría impar:
\[\angle H(-f)= -\angle H(f) \nonumber \]
Estas propiedades de este ejemplo específico se aplican a todas las funciones de transferencia asociadas a los circuitos. En consecuencia, no necesitamos trazar el componente de frecuencia negativa; sabemos lo que es a partir de la parte de frecuencia positiva.
La magnitud es igual a\[\frac{1}{\sqrt{2}} \nonumber \] su ganancia máxima (1 a f=0) cuando 2π FrC =1 (los dos términos en el denominador de la magnitud son iguales). La frecuencia
\[f_{c}=\frac{1}{2\pi RC} \nonumber \]
define el límite entre dos rangos de operación.
- Para frecuencias por debajo de esta frecuencia, el circuito no altera mucho la amplitud de la fuente exponencial compleja.
- Para frecuencias mayores a f c el circuito atenúa fuertemente la amplitud. Así, cuando la frecuencia de la fuente está en este rango, la salida del circuito tiene una amplitud mucho menor que la de la fuente.
Por estas razones, esta frecuencia se conoce como la frecuencia de corte. En este circuito la frecuencia de corte depende únicamente del producto de la resistencia y la capacitancia. Por lo tanto, se produce una frecuencia de corte de 1 kHz cuando:
\[\frac{1}{2\pi RC}=10^{3} \nonumber \]
o
\[RC=\frac{10^{-3}}{2\pi }=1.59\times 10^{4} \nonumber \]
Así, las combinaciones resistencia-capacitancia de 1.59 kΩ y 100 nF o 10 Ω y 1.59 μF dan como resultado la misma frecuencia de corte.
El desplazamiento de fase causado por el circuito a la frecuencia de corte es exactamente igual a -π/4. Por lo tanto, por debajo de la frecuencia de corte, la fase se ve poco afectada, pero a frecuencias más altas, el desplazamiento de fase causado por el circuito se convierte en -π/2. Este desplazamiento de fase corresponde a la diferencia entre un coseno y un seno.
Podemos usar la función de transferencia para encontrar la salida cuando el voltaje de entrada es sinusoidal por dos razones. En primer lugar, una sinusoide es la suma de dos exponenciales complejos, teniendo cada uno una frecuencia igual a la negativa del otro. En segundo lugar, debido a que el circuito es lineal, se aplica la superposición. Si la fuente es una onda sinusoidal, sabemos que
\[v_{in}(t)=A\sin (2\pi ft) \nonumber \]
\[v_{in}(t)=\frac{A}{2i}\left ( e^{i2\pi ft}-e^{-(i2\pi ft)} \right ) \nonumber \]
Dado que la entrada es la suma de dos exponenciales complejos, sabemos que la salida también es una suma de dos exponenciales complejos similares, siendo la única diferencia que la amplitud compleja de cada uno se multiplica por la función de transferencia evaluada a la frecuencia de cada exponencial.
\[v_{out}(t)=\frac{A}{2i}H(f)e^{i2\pi ft}-\frac{A}{2i}H(-f)e^{-(i2\pi ft)} \nonumber \]
Como se señaló anteriormente, la función de transferencia se expresa más convenientemente en forma polar:
\[H(f)=\left | H(f) \right |e^{i\angle H(f)} \nonumber \]
Además,
\[\left | H(-f) \right |=\left | H(f) \right | \nonumber \]
(incluso simetría de la magnitud) y
\[\angle H(-f)= -\angle H(f) \nonumber \]
(simetría impar de la fase). La expresión del voltaje de salida simplifica a
\[v_{out}(t)=\frac{A}{2i}\left |H(f) \right |e^{i2\pi ft+\angle H(f)}-\frac{A}{2i}\left | H(f) \right |e^{(-(i2\pi ft))-\angle H(f)} \nonumber \]
\[v_{out}(t)=A\left | H(f) \right |\sin \left ( 2\pi ft+\angle (H(f)) \right ) \nonumber \]
La salida del circuito a una entrada sinusoidal también es una sinusoide, teniendo una ganancia igual a la magnitud de la función de transferencia del circuito evaluada a la frecuencia fuente y una fase igual a la fase de la función de transferencia en la frecuencia de origen. Resultará que esta descripción de relación entrada-salida se aplica a cualquier circuito lineal que tenga una fuente sinusoidal.
Esta propiedad input-output es un caso especial de un resultado más general. Mostrar que si la fuente puede escribirse como la parte imaginaria de un exponencial complejo\[v_{in}(t)=\Im (Ve^{i2\pi ft}) \nonumber \] la salida viene dada por\[v_{out}(t)=\Im (VH(f)e^{i2\pi ft}) \nonumber \] Mostrar que un resultado similar también se mantiene para la parte real.
Solución
La noción clave es escribir la parte imaginaria como la diferencia entre un exponencial complejo y su conjugado complejo:
\[\Im (Ve^{i2\pi ft})=\frac{Ve^{i2\pi ft}-\overline{V}e^{-(i2\pi ft)}}{2i} \nonumber \]
La respuesta a\[Ve^{i2\pi ft} \nonumber \] es\[VH(f)e^{i2\pi ft} \nonumber \]
lo que significa que la respuesta a\[\overline{V}e^{-(i2\pi ft)} \nonumber \] es\[\overline{V}H(-f)e^{-(i2\pi ft)} \nonumber \]
Como dice\[H(-f)=\overline{H(f)} \nonumber \] el Principio de Superposición que la salida a la parte imaginaria es\[\Im \left ( VH(f)e^{i2\pi ft} \right ) \nonumber \]
El mismo argumento sostiene para la parte real:
\[\Re (Ve^{i2\pi ft})\rightarrow \Re \left ( VH(f)e^{i2\pi ft} \right ) \nonumber \]
La noción de impedancia surge cuando asumimos que las fuentes son exponenciales complejas. Esta suposición puede parecer restrictiva; ¿qué haríamos si la fuente fuera un paso unitario? Cuando usamos impedancias para encontrar la función de transferencia entre la variable de origen y salida, podemos derivar de ella la ecuación diferencial que relaciona entrada y salida. La ecuación diferencial se aplica sin importar cuál sea la fuente. Como hemos argumentado, es mucho más sencillo usar impedancias para encontrar la ecuación diferencial (porque podemos usar reglas de combinación de series y paralelas) que cualquier otro método. En este sentido, no hemos perdido nada al pretender temporalmente que la fuente es un exponencial complejo.
De hecho, ¡también podemos resolver la ecuación diferencial usando impedancias! Así, a pesar de la aparente restrictividad de las impedancias, asumir fuentes exponenciales complejas es en realidad bastante general.


