3.14: Diseño de funciones de transferencia
- Page ID
- 85500
- Este módulo resume los conceptos clave de las funciones de transferencia e incluye ejemplos de uso de funciones de transferencia.
Si la fuente consiste en dos (o más) señales, sabemos por teoría de sistemas lineales que el voltaje de salida es igual a la suma de las salidas producidas por cada señal sola. En definitiva, los circuitos lineales son un caso especial de sistemas lineales, por lo que se aplica la superposición. En particular, supongamos que estas señales componentes son exponenciales complejas, cada una de las cuales tiene una frecuencia diferente a las demás. La función de transferencia retrata cómo el circuito afecta la amplitud y fase de cada componente, lo que nos permite entender cómo funciona el circuito en una señal complicada. Aquellos componentes que tienen una frecuencia menor que la frecuencia de corte pasan a través del circuito con poca modificación mientras que los que tienen frecuencias más altas se suprimen. Se dice que el circuito actúa como un filtro, filtrando la señal fuente en función de la frecuencia de cada componente exponencial complejo. Debido a que las frecuencias bajas pasan por el filtro, lo llamamos filtro de paso bajo para expresar con mayor precisión su función.
También hemos encontrado la facilidad de calcular la salida para entradas sinusoidales mediante el uso de la función de transferencia. Una vez que encontramos la función de transferencia, podemos escribir la salida directamente como lo indica la salida de un circuito para una entrada sinusoidal.
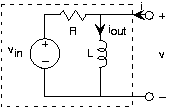
Apliquemos estos resultados a un ejemplo final, en el que la entrada es una fuente de voltaje y la salida es la corriente del inductor. El voltaje de la fuente es igual a:
\[V_{in}=2\cos (2\pi 60t)+3 \nonumber \]
Queremos que el circuito pase voltaje constante (offset) esencialmente inalterado (salvo por el hecho de que la salida es una corriente en lugar de una tensión) y elimine el término de 60 Hz. Debido a que la entrada es la suma de dos sinusoides, una constante es un coseno de frecuencia cero, nuestro enfoque es
- encontrar la función de transferencia usando impedancias
- usarlo para encontrar la salida debido a cada componente de entrada
- agregar los resultados
- encontrar valores de elementos que cumplan con nuestros criterios de diseño
Debido a que el circuito es una combinación de elementos en serie, usemos el divisor de voltaje para encontrar la función de transferencia entre V in y V, luego use la relación v-i del inductor para encontrar su corriente.
\[\frac{I_{out}}{V_{in}}=\frac{i2\pi fL}{R+i2\pi fL}\frac{1}{i2\pi fL} \nonumber \]
\[\frac{I_{out}}{V_{in}}=\frac{1}{i2\pi fL+R} \nonumber \]
\[\frac{I_{out}}{V_{in}}=H(f) \nonumber \]
donde divisor de voltaje
\[voltage\; \; divider=\frac{i2\pi fL}{R+i2\pi fL} \nonumber \]
\[inductor\; \; admittance=\frac{1}{i2\pi fL} \nonumber \]
[¿Comprueban las unidades?] La forma de esta función de transferencia debe ser familiar; es un filtro de paso bajo, y realizará nuestra función deseada una vez que elegimos los valores de los elementos correctamente.
El término constante es más fácil de manejar. La salida viene dada por:
\[3\left | H(0) \right |=\frac{3}{R} \nonumber \]
Así, el valor que elegimos para la resistencia determinará el factor de escalado de cómo se convierte el voltaje en corriente. Para la señal componente de 60 Hz, la corriente de salida es
\[2\left | H(60) \right |\cos \left ( 2\pi 60t+\angle (H(60)) \right ) \nonumber \]
El resultado total debido a nuestra fuente es:
\[i_{out}=2\left | H(60) \right |\cos \left ( 2\pi 60t+\angle (H(60)) \right )+3\times H(0) \nonumber \]
La frecuencia de corte para este filtro ocurre cuando las partes real e imaginaria del denominador de la función de transferencia se igualan entre sí. Así,
\[2\pi f_{c}L=R \nonumber \]
\[f_{c}=\frac{R}{2\pi L} \nonumber \]
Queremos que esta frecuencia de corte sea mucho menor a 60 Hz. Supongamos que lo colocamos a, digamos, 10 Hz. Esta especificación requeriría que los valores de los componentes estén relacionados por
\[\frac{R}{L}=20\pi =62.8 \nonumber \]
La función de transferencia a 60 Hz sería
\[\left | \frac{1}{i2\pi 60L+R} \right |=\frac{1}{R}\left | \frac{1}{6i+1} \right |=\frac{1}{R}\frac{1}{\sqrt{37}}\simeq 0.16\times \frac{1}{R} \nonumber \]
que produce una atenuación (relativa a la ganancia a frecuencia cero) de aproximadamente 1/6, y da como resultado una amplitud de salida de 0.3/R relativa a la amplitud del término constante de 3/R. Un factor de 10 tamaño relativo entre los dos componentes parece razonable. Tener un inductor de 100 mH requeriría una resistencia de 6.28 Ω. Un valor de resistencia fácilmente disponible es 6.8 Ω; por lo tanto, esta elección resulta en piezas compradas de manera económica y fácil. Para hacer que la resistencia sea más grande requeriría un inductor proporcionalmente mayor. Desafortunadamente, incluso un inductor de 1 H es físicamente grande; en consecuencia, las frecuencias de corte bajas requieren resistencias de pequeño valor e inductores de gran valor. La elección que se hace aquí representa solo un compromiso.
La fase del componente de 60 Hz estará muy cerca de -π/2 dejando que sea:
\[\frac{0.3}{R}\cos \left ( 2\pi 60t-\frac{\pi }{2} \right )=\frac{0.3}{R}\sin (2\pi 60t) \nonumber \]
Las formas de onda para la entrada y salida se muestran a continuación:
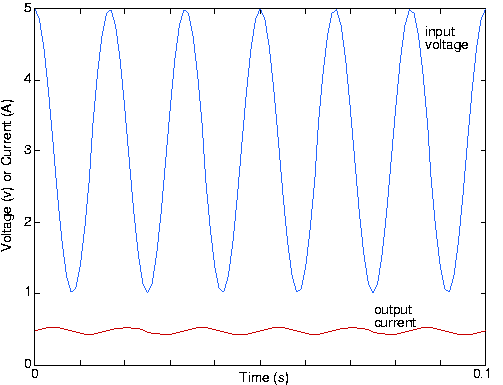
Tenga en cuenta que la fase de la sinusoide de hecho ha cambiado; el filtro de paso bajo no solo redujo la amplitud de la señal de 60 Hz, sino que también cambió su fase en 90°.


