5.4: Cuantización de Amplitud
- Page ID
- 85330
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Conversión de analógico a digital.
El Teorema de Muestreo dice que si muestreamos una señal de banda limitada s (t) lo suficientemente rápido, se puede recuperar sin error de sus muestras
\[s(nT_{s}),n\in \left \{ ...,-1,0,1,... \right \} \nonumber \]
El muestreo es solo la primera fase de adquisición de datos en una computadora: El procesamiento computacional requiere además que las muestras sean cuantificadas: los valores analógicos se convierten en forma digital. En definitiva, habremos realizado conversión analógico-digital (A/D).
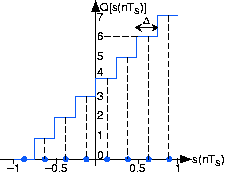
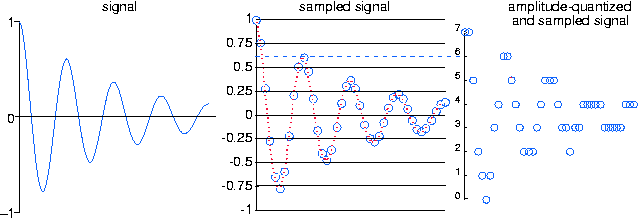
Un fenómeno que recuerda a los errores incurridos al representar números en una computadora evita que las amplitudes de señal se conviertan sin error en una representación numérica binaria. En la conversión analógico-digital, se supone que la señal se encuentra dentro de un rango predefinido. Suponiendo que podemos escalar la señal sin afectar la información que expresa, definiremos este rango para que sea [-1,1]. Además, el convertidor A/D asigna valores de amplitud en este rango a un conjunto de números enteros. Un convertidor de bits B produce uno de los enteros
\[\left \{0,1,...,2^{B} -1\right \} \nonumber \]
para cada entrada muestreada. La Figura 5.4.1 muestra cómo un convertidor A/D de tres bits asigna valores de entrada a los enteros. Definimos un intervalo de cuantificación para ser el rango de valores asignados al mismo entero. Así, para nuestro ejemplo convertidor A/D de tres bits, el intervalo de cuantificación Δ es 0.25; en general, es 2/2 B.
Recordando la trama de máximos diarios promedio en este problema de dominio de frecuencia, ¿por qué esta trama es tan dentado? Interpretar este efecto en términos de conversión analógico-digital.
Solución
Las temperaturas trazadas se cuantificaron al grado más cercano. Así, la amplitud de alta temperatura se cuantificó como una forma de conversión A/D.
Debido a que los valores que se encuentran en cualquier lugar dentro de un intervalo de cuantificación se les asigna el mismo valor para el procesamiento informático, el valor de amplitud original no se puede recuperar sin error Por lo general, el convertidor D/A, el dispositivo que convierte enteros en amplitudes, asigna una amplitud igual al valor que se encuentra a mitad de camino en el intervalo de cuantificación. El entero 6 se asignaría a la amplitud 0.625 en este esquema. El error introducido al convertir una señal de forma analógica a digital por muestreo y cuantificación de amplitud entonces de nuevo sería la mitad del intervalo de cuantificación para cada valor de amplitud. Así, el llamado error A/D equivale a la mitad del ancho de un intervalo de cuantificación: 1/2 B. Como hemos fijado el rango de amplitud de entrada, cuantos más bits estén disponibles en el convertidor A/D, menor será el error de cuantificación.
Para analizar más profundamente el error de cuantificación de amplitud, necesitamos calcular la relación señal/ruido, que es igual a la relación entre la potencia de la señal y la potencia del error de cuantificación. Suponiendo que la señal es una sinusoide, la potencia de la señal es el cuadrado de la amplitud rms:
\[power(s)=\left ( \frac{1}{\sqrt{2}} \right )^{2}=\frac{1}{2} \nonumber \]
La Figura 5.4.2 detalla un único intervalo de cuantificación.
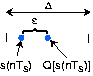
Su ancho es\(Δ\) y el error de cuantificación se denota por\(\varepsilon\). Para encontrar la potencia en el error de cuantificación, observamos que no importa en qué intervalo de cuantificación caiga el valor de la señal, el error tendrá las mismas características. Para calcular el valor rms, debemos cuadrar el error y promediarlo a lo largo del intervalo.
\[\begin{align*} rms(\varepsilon) &=\sqrt{\frac{1}{\Delta }\int_{-\Delta }^{\Delta }\varepsilon ^{2}d\varepsilon } \\[4pt] &=\left ( \frac{\Delta ^{2}}{12} \right )^{\frac{1}{2}} \end{align*} \]
Dado que el ancho del intervalo de cuantificación para un convertidor de bits B es igual
\[\dfrac{2}{2^{B}}=2^{-(B-1)} \nonumber \]
encontramos que la relación señal/ruido para el proceso de conversión analógico-digital es igual
\[SNR=\frac{\frac{1}{2}}{\frac{2^{-(2(B-1))}}{12}}=\frac{3}{2}2^{2B}=6B+\log 1.5dB \nonumber \]
Por lo tanto, cada aumento de bit en el convertidor A/D produce un aumento de 6 dB en la relación señal/ruido. El término constante 10 log1.5 equivale a 1.76.
Esta derivación asumió que la amplitud de la señal estaba en el rango [-1,1]. ¿Cuál sería la relación señal-ruido de cuantificación de amplitud si estuviera en el rango [-A, A]?
Solución
La relación señal/ruido no depende de la amplitud de la señal. Con un rango A/D de [-A, A] el intervalo de cuantificación
\[\Delta =\frac{2A}{2^{B}} \nonumber \]
y el valor rms de la señal (asumiendo de nuevo que es una sinusoide) es
\[\frac{A}{\sqrt{2}} \nonumber \]
¿Cuántos bits se requerirían en el convertidor A/D para garantizar que el error de cuantificación de amplitud máxima sea menor que 60 db menor que el valor pico de la señal?
Solución
Resolviendo
\[2^{-B}=0.001 \nonumber \]
resultados en
\[B=10\; bits \nonumber \]
La música en un CD se almacena con una precisión de 16 bits. ¿A qué relación señal/ruido corresponde esto?
Solución
Un convertidor A/D de 16 bits produce una SNR de
\[6\times 16+10\log 1.5=97.8dB \nonumber \]
Una vez que hemos adquirido las señales con un convertidor A/D, podemos procesarlas usando hardware o software digital. Se puede demostrar que si el procesamiento por computadora es lineal, el resultado del muestreo, procesamiento por computadora y no muestreo es equivalente a algún sistema lineal analógico. ¿Por qué ir a toda la molestia si la misma función se puede lograr usando técnicas analógicas? Saber cuándo sobresale el procesamiento digital y cuándo no es un tema importante.


