2.4: Analogías

Debido a que las abstracciones son tan útiles, es útil contar con métodos para hacerlas. Una manera es construir una analogía entre dos sistemas. Cada característica común conduce a una abstracción; cada abstracción conecta nuestro conocimiento en un sistema con nuestro conocimiento en el otro sistema. Una pieza de conocimiento tiene doble deber. Como una palanca mental, la analogía y, más generalmente, la abstracción son amplificadores de inteligencia.

2.4.1 Analogías eléctrico-mecánicas

Una ilustración con muchas abstracciones sobre las que podemos practicar es la analogía entre un sistema de muelle-masa y un circuito inductor-condensador (LC).

En el circuito, la fuente de voltaje, la V _en su lado izquierdo, suministra una corriente que fluye a través del inductor (un cable envuelto alrededor de una varilla de hierro) y el condensador (dos placas de metal separadas por aire). A medida que la corriente fluye a través del condensador, altera la carga en el condensador. Esta “carga” se llama confusamente, porque la carga neta en el condensador permanece cero. En cambio, “carga” significa que las dos placas del condensador mantienen cargas opuestas, Q y -Q, con Q ≠ 0. Los cambios actuales Q. Las cargas en las dos placas crean un campo eléctrico, que produce el voltaje de salida V igual a Q/C (donde C es la capacitancia).

Para la mayoría de nosotros, el circuito es menos familiar que el sistema resorte-masa. Sin embargo, al construir una analogía entre los sistemas, transferimos nuestra comprensión de lo mecánico al sistema eléctrico.

En el sistema mecánico, la variable fundamental es el desplazamiento x de la masa. En el sistema eléctrico, es la carga Q en el condensador. Estas variables son análogas por lo que sus derivadas también deben ser análogas: velocidad (v), la derivada de posición, debe ser análoga a la corriente (I), la derivada de carga.

Construyamos más puentes de analogía. La derivada de la velocidad, que es la segunda derivada de la posición, es la aceleración (a). Por lo tanto, la derivada de la corriente (dI/dt) es el análogo de la aceleración. Esta analogía será útil en breve cuando encontremos la frecuencia de oscilación del circuito.

Estas variables describen el estado de los sistemas y cómo cambia ese estado: Son la cinemática. Pero sin las causas del movimiento —la dinámica— los sistemas permanecen sin vida. En el sistema mecánico, la dinámica resulta de la fuerza, que produce aceleración:

\[a = \frac{F}{m}\]

La aceleración es análoga al cambio en la corriente dI/ dt, que se produce aplicando una tensión al inductor. Para un inductor, la relación gobernante (análoga a la ley de Ohm para una resistencia) es

\[\frac{dI}{dt} = \frac{V}{L}\]

donde L es la inductancia y V es el voltaje a través del inductor. Con base en la estructura común de las dos relaciones, la fuerza F y la tensión V deben ser análogas. En efecto, ambos miden el esfuerzo: Force intenta acelerar la masa, y el voltaje intenta cambiar la corriente del inductor. De igual manera, la masa y la inductancia son análogas: Ambos miden la resistencia al esfuerzo correspondiente. Las masas grandes son difíciles de acelerar y los inductores L grandes resisten los cambios en su corriente. (Una masa y un inductor, en otra similitud, ambos representan energía cinética: una masa a través de su movimiento, y un inductor a través de la energía cinética de los electrones que forman su campo magnético).

Pasando de la analogía masa-inductor, veamos la analogía de resorte-condensador. Estos componentes representan la energía potencial en el sistema: en el resorte a través de la energía en su compresión o expansión, y en el condensador a través de la energía potencial electrostática debida a su carga.

Force intenta estirar el resorte pero encuentra una resistencia k: Cuanto más rígido es el resorte (cuanto mayor es su k), más difícil es estirarse.

\[x = \frac{F}{k}\]

Análogamente, el voltaje intenta cargar el condensador pero cumple con una resistencia 1/ C: Cuanto mayor sea el valor de 1/ C, menor será la carga resultante.

\[Q = \frac{V}{1/C}\]

Con base en la estructura común de las relaciones para x y Q, la constante elástica k debe ser análoga a la capacitancia inversa 1/ C. Aquí están todas nuestras analogías.

De esta tabla, podemos leer nuestro resultado clave. Comience con la frecuencia natural (angular)\(\omega\) de un sistema de muelle-masa:\(\omega = \frac{k}{m}\) Luego aplique las analogías. La masa m es análoga a la inductancia L. La constante de resorte k es análoga a la capacitancia inversa 1/ C. Por lo tanto,\(\omega\) para el circuito LC es 1/ LC:

\[\omega = \sqrt\frac{1/C}{L} = \frac{1}{\sqrt{LC}}\]

Debido a los puentes de analogía, una fórmula, la frecuencia natural de un sistema de muelle-masa, tiene doble función. De manera más general, cualquier cosa que aprendamos sobre un sistema nos ayuda a entender el otro sistema. Debido a las analogías, cada pieza de conocimiento cumple una doble función.

2.4.2 Densidad de energía en el campo gravitacional

Con la analogía eléctrico-mecánica como práctica, probemos una analogía menos familiar: entre el campo eléctrico y el gravitacional. En particular, conectaremos las densidades de energía (energía por volumen) en los campos correspondientes. Un campo eléctrico E representa una densidad de energía de\(\epsilon_{0}E^{2}/2\), donde\(\epsilon_{0}\) es la permitividad del espacio libre que aparece en la fuerza electrostática entre dos cargas q ₁ y q ₂:

\[F = \frac{q_{1}q_{2}}{4 \pi \epsilon_{0} r^{2}}\]

Debido a que las fuerzas electrostáticas y gravitacionales son ambas fuerzas cuadradas inversas (la fuerza es proporcional a 1/r ²), las densidades de energía deben ser análogas. No menos importante, debería haber una densidad de energía gravitacional. Pero, ¿cómo se relaciona con el campo gravitacional?

Para responder a esa pregunta, nuestro primer paso es encontrar el análogo gravitacional del campo eléctrico. En lugar de pensar en el campo eléctrico sólo como algo eléctrico, enfocarse en la idea común de un campo. En ese sentido, el campo eléctrico es el objeto que, al multiplicarse por la carga, da la fuerza:

\[\textrm{force = charge} \times \textrm{field}\]

Usamos palabras en lugar de los símbolos normales, como E para campo o q para carga, porque los símbolos podrían unir nuestro pensamiento a casos particulares y evitar que subamos la escalera de abstracción.

Esta forma verbal nos impulsa a preguntarnos: ¿Qué es la carga gravitacional? En electrostática, la carga es la fuente del campo. En la gravitación, la fuente del campo es la masa. Por lo tanto, la carga gravitacional es masa. Debido a que el campo es fuerza por carga, la intensidad del campo gravitacional es una aceleración:

\[gravitational \: field = \frac{force}{charge} = \frac{force}{mass} = acceeration\]

En efecto, en la superficie de la Tierra, la fuerza de campo es g, también llamada aceleración por gravedad.

La definición de campo gravitacional es la primera mitad del rompecabezas (estamos utilizando de nuevo el razonamiento de división y conquista). Para la segunda mitad, usaremos el campo para calcular la densidad de energía. Para ello, revisemos la ruta del campo eléctrico a la densidad de energía electrostática:

\[E \rightarrow \frac{1}{2} \epsilon_{0} E^{2}\]

Con g como campo gravitacional, la ruta análoga es

\[g \rightarrow \frac{1}{2} \times somethings \times g^{2}\]

donde el “algo” representa nuestra ignorancia de qué hacer al respecto\(\epsilon_{0}\).

¿De qué es el equivalente gravitacional\(\epsilon_{0}\)?

Para encontrar su equivalente, compare el caso más simple en ambos mundos: el campo de una carga puntual. Una carga eléctrica puntual q produce un campo

\[E = \frac{1}{4 \pi \epsilon_{0}}\frac{q}{r^{2}}\]

Una carga gravitacional puntual m (una masa puntual) produce un campo gravitacional (una aceleración)

\[g = \frac{Gm}{r^{2}}\]

donde G es la constante de Newton.

El campo gravitacional tiene una estructura similar al campo eléctrico. Ambas son fuerzas inverso-cuadrado, como se esperaba. Ambos son proporcionales a la carga. La diferencia es la constante de proporcionalidad. Para el campo eléctrico, lo es\(\frac{1}{4 \pi \epsilon_{0}}\). Para el campo gravitacional, es simplemente G. Por lo tanto, G es análogo a\(\frac{1}{4 \pi \epsilon_{0}}\); equivalentemente,\(\epsilon_{0}\) es análogo a\(\frac{1}{4 \pi G}\).

Entonces la densidad de energía gravitacional se convierte

\[\frac{1}{2} \times \frac{1}{4 \pi G} \times g^{2} = \frac{g^{2}}{8 \pi G}\]

Utilizaremos esta analogía en la Sección 9.3.3 cuando transferimos nuestro conocimiento duramente ganado de la radiación electromagnética para comprender la física aún más sutil de la radiación gravitacional.

Ejercicio\(\PageIndex{1}\): Gravitational energy of the Sun

¿Cuál es la energía en el campo gravitacional del Sol? (Basta con considerar el campo fuera del Sol.)

Ejercicio\(\PageIndex{2}\): Pendulum period including buoyancy

El periodo de un péndulo en vacío es (para pequeñas amplitudes)\(T = 2 \pi \sqrt \frac{l}{g}\), donde l es la longitud del bob y g es la intensidad del campo gravitacional. Ahora imagina el péndulo balanceándose en un fluido (digamos, aire). Al reemplazar g por un valor modificado, incluir el efecto de flotabilidad en la fórmula para el periodo del péndulo.

Ejercicio\(\PageIndex{3}\): Comparing field energies

Encuentra la relación de energías de campo eléctrico a gravitacional en los campos producidos por un protón.

2.4.3 Combinación paralela

Las analogías no solo reutilizan el trabajo, sino que nos ayudan a reescribir expresiones en formas compactas y perspicaces. Un ejemplo es la idea de combinación paralela. Aparece en el análisis de la escalera resistiva infinita del Problema 2.8.

Para encontrar la resistencia R a través de la escalera (es decir, lo que mide el ohmímetro entre los nodos A y B), se representa toda la escalera como una sola resistencia R. Entonces toda la escalera es de 1 ohm en serie con la combinación paralela de 1 ohm y R:

El siguiente paso para encontrar R suele invocar la fórmula de resistencia paralela: que la resistencia de _R1 y _R2 en paralelo es

\[\frac{R_{1}R_{2}}{R_{1} + R_{2}}\]

Para nuestra escalera resistiva, la combinación paralela de 1 ohm con la escalera es de 1 ohm × R/(1 ohm + R). Colocar esta combinación en serie con 1 ohm da una resistencia

\[1 \Omega + \frac{1 \Omega \times R}{1 \Omega + R}\]

Esta construcción recursiva reproduce la escalera, solo una unidad más larga. Por lo tanto, obtenemos una ecuación para R:

\[R = 1 \Omega + \frac{1 \Omega \times R}{1 \Omega + R}\]

La solución (positiva) es\(R = (1 + \sqrt 5 )/2\) ohmios. La parte numérica es la proporción áurea\(\phi\) (aproximadamente 1.618). Así, la escalera, cuando está construida con resistencias de 1 ohmios, ofrece una resistencia de\(\phi\) ohmios.

Aunque la solución es correcta, se salta sobre una idea reutilizable: la combinación paralela. Para facilitar su reutilización, pongamos la idea con una notación:

\[R_{1} \parallel R_{2}\]

Esta notación es autodocumentante, siempre y cuando reconozca que el símbolo\(\parallel\) significa “paralelo”, un reconocimiento promovido por las barras paralelas. Una buena notación debería ayudar a pensar, no obstaculizarlo al exigirnos que recordemos cómo funciona la notación. Con esta notación, la ecuación para la resistencia de escalera R es

\[R = 1 \Omega + 1 \Omega \parallel R\]

(El operador de combinación paralela tiene mayor prioridad que, se calcula antes, la suma). Esta expresión refleja más claramente la estructura del sistema, y nuestro razonamiento al respecto, que la versión

\[R = 1 \Omega + \frac{1 \Omega \times R}{1 \omega + R}\].

La\(\parallel\) notación organiza la complejidad.

Una vez que nombras una idea, la encuentras en todas partes. Cuando era niño, después de que mi familia compró un Volvo, vi Volvos en todas las calles. Del mismo modo, ahora veremos ejemplos de combinación paralela mucho más allá de la apariencia original de la idea en los circuitos. Por ejemplo, da la constante de resorte de dos resortes conectados (Problema 2.16):

Ejercicio\(\PageIndex{4}\): Springs as capacitors

Usando la analogía entre resortes y capacitores (discutida en la Sección 2.4.1), explique por qué los resortes en serie se combinan usando la combinación paralela de sus constantes de resorte.

Otro ejemplo sorprendente es el siguiente sistema resorte-masa con dos masas:

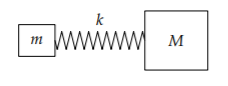
La frecuencia natural\(\omega\), expresada sin nuestra\(\parallel\) abstracción, es

\[\omega = \frac{k(m + M)}{mM}\]

Esta forma parece complicada hasta que usamos la\(\parallel\) abstracción:

\[\omega = \frac{k}{m \parallel M}\]

Ahora la frecuencia tiene más sentido. Las dos masas actúan como su combinación paralela\(m \parallel M\)

La masa de reemplazo\(m \parallel M\) es tan útil que tiene un nombre especial: la masa reducida. Nuestra abstracción organiza la complejidad al convertir un sistema de tres componentes (un resorte y dos masas) en un sistema de dos componentes más simple.

En el espíritu de la notación que promueve la penetración, use m minúscula (“pequeña”) para la masa que probablemente sea más pequeña, y M en mayúscula (“grande”) para la masa que probablemente sea más grande. Entonces escribe\(m \parallel M\) en lugar de\(M \parallel m\). Estas dos formas producen el mismo resultado, pero el\(m \parallel M\) orden minimiza la sorpresa: La combinación paralela de m y M es menor que cualquiera de las masas (Problema 2.17), por lo que está más cerca de m, la masa más pequeña, que de M. Escribir\(m \parallel M\), más que\(M \parallel m\), coloca primero la información más destacada.

Ejercicio\(\PageIndex{5}\): Using the resistance analogy

Mediante el uso de la analogía con las resistencias paralelas, explique por qué\(m \parallel M\) es menor que m y M.

¿Por qué las dos masas se combinan como resistencias en paralelo?

La respuesta radica en la analogía entre masa y resistencia. La resistencia aparece en la ley de Ohm:

voltaje = resistencia × corriente.

El voltaje es un esfuerzo. La corriente, que resulta del esfuerzo, es un flujo. Por lo tanto, la forma más general, un paso más arriba en la escalera de abstracción, es

esfuerzo = resistencia × flujo.

En esta forma, la segunda ley de Newton,

fuerza = masa × aceleración

identifica la fuerza como el esfuerzo, la masa como la resistencia y la aceleración como el flujo.

Debido a que el resorte puede menear cualquier masa, así como la corriente puede fluir a través de cualquiera de las dos resistencias paralelas, el resorte siente una resistencia igual a la combinación paralela de las resistencias, es decir,\(m \parallel M\).

Ejercicio\(\PageIndex{6}\): Three springs connected

¿Cuál es la constante elástica efectiva de tres resortes conectados en una línea, con constantes de resorte 2, 3 y 6 newtons por metro, respectivamente?

2.4.4 Impedancia como abstracción de nivel superior

La resistencia, en el sentido eléctrico, ha aparecido varias veces, y subyace a una abstracción de mayor nivel: la impedancia. Impedancia extiende la idea de resistencia eléctrica a capacitores e inductores. Capacitores e inductores, junto con las resistencias, son los tres elementos de circuito lineal: En estos elementos, la conexión entre corriente y voltaje se describe mediante una ecuación lineal: Forresistors, es una relación algebraica lineal (ley de Ohm); para condensadores o inductores, es una ecuación diferencial lineal.

¿Por qué deberíamos extender la idea de resistencia?

Las resistencias son fáciles de manejar. Cuando un circuito contiene solo resistencias, podemos describir inmediata y completamente cómo se comporta. En particular, podemos escribir la tensión en cualquier punto del circuito como una combinación lineal de las tensiones en los nodos fuente. Si tan solo pudiéramos hacer lo mismo cuando el circuito contiene capacitores e inductores.

¡Podemos! Comience con la ley de Ohm,

\[\textrm{current} = \frac{voltage}{resistance}\],

y mírelo en el nivel superior y la forma expandida

\[flow = \frac{1}{resistance} \times effort\]

Para un condensador, el flujo seguirá siendo corriente. Pero tendremos que encontrar el análogo capacitivo del esfuerzo. Esta analogía resultará ligeramente diferente de la analogía eléctrico-mecánica entre capacitancia y constante de resorte (Sección 2.4.1), porque ahora estamos haciendo una analogía entre condensadores y resistencias (y, eventualmente, inductores). Para un condensador,

\[charge = capacitance \times voltage\]

Para convertir la carga en corriente, diferenciamos ambos lados para obtener

\[\textrm{current} = \textrm{capacitance} \times \frac{d\textrm{(voltage)}}{dt}\]

Para hacer la analogía cuantitativa, apliquemos al condensador el voltaje más simple cuya forma no se ve alterada por diferenciación:

\[V = V_{0}e^{j \omega t}\]

donde V es la tensión de entrada, V ₀ es la amplitud,\(\omega\) es la frecuencia angular y j es la unidad imaginaria\(\sqrt -1\). El voltaje V es un número complejo; pero el entendimiento implícito es que el voltaje real es la parte real de este número complejo. Al encontrar cómo la corriente I (el flujo) depende de V (el esfuerzo), extenderemos la idea de resistencia a un condensador.

Con esta forma exponencial, ¿cómo podemos representar los voltajes oscilantes más familiares V ₁ cos\(\omega\) t o V ₁ sin\(\omega\) t, donde V ₁ es un voltaje real?

Comienza con la relación de Euler:

\[e^{j \omega t} = \cos \omega t + j \sin \omega t \]

Para hacer V ₁ cos\(\omega\) t, establecer\(V_{0} = V_{1}\) en\(V = V_{0} e^{j \omega t}\). Entonces

\[V= V_{1}(\cos \omega t + j \sin \omega t)\]

y la parte real de V es solo V ₁ cos\(\omega\) t.

Hacer V ₁ sin\(omega\) t es más complicado. Elegir\(V_{0} = j V_{1}\) casi funciona:

\[V= j V_{1} (\cos \omega t + j \sin \omega t) = V_{1} (j \cos \omega t - \sin \omega t)\].

La parte real es\(-V_{1} \sin \omega t\), que es correcta excepto por el signo menos. Así, la amplitud correcta es\(V_{0} = -jV_{1}\). En resumen, nuestra forma exponencial puede representar de manera compacta las señales sinusoidales y cosenales más familiares.

Con esta forma exponencial, la diferenciación es más simple que con senos o cosenos. Diferenciar V con respecto al tiempo solo hace bajar un factor de\(j \omega\), pero por lo demás deja el\(V_{0} e^{j \omega t}\) solo:

\[\frac{dV}{dt} = j \omega \times V_{0} e^{j \omega t} = j \omega V\]

Con este voltaje cambiante, la ecuación del condensador,

\[current = capacitance \times \frac{d(voltage)}{dt}\]

se convierte

\[current = capacitance \times j \omega \times voltage\]

Comparemos esta forma con su análogo para una resistencia (ley de Ohm):

\[current = \frac{1}{resistance} \times voltage\]

Emparejando las piezas, encontramos que un condensador ofrece una resistencia

\[Z_{C} = \frac{1}{j \omega C}\]

Esta resistencia más general, que depende de la frecuencia, se denomina impedancia y se denota Z. (En la analogía de la Sección 2.4.1 entre condensadores y resortes, encontramos que el condensador ofrecía una resistencia a ser cargado de 1/ C. La impedancia, el resultado de una analogía entre condensadores y resistencias, contiene 1/ C también, pero también contiene la frecuencia en el\(\omega\) factor 1/ j).

Usando impedancia, podemos describir lo que sucede con cualquier señal sinusoidal en un circuito que contiene condensadores. Nuestro pensamiento es ayudado por la notación compacta: la impedancia capacitiva ZC (o incluso RC). La notación oculta los detalles de la ecuación diferencial del condensador y nos permite transferir nuestra intuición sobre la resistencia y el flujo a una clase más amplia de circuitos.

El circuito más simple con resistencias y condensadores es el llamado circuito RC de paso bajo. No sólo es el circuito interesante más simple, también será, gracias a otras analogías, un modelo para el flujo de calor. Apliquemos la analogía de impedancia a este circuito.

Para ayudarnos a hacer y utilizar abstracciones, imaginemos desenfocar nuestros ojos. Bajo visión borrosa, el condensador parece una resistencia que simplemente tiene una resistencia divertida\(RC = \frac{1}{j \omega C}\). Ahora todo el circuito se ve igual que un circuito de pura resistencia. En efecto, es el circuito más simple de este tipo, un divisor de voltaje. Su comportamiento se describe por un número: la ganancia, que es la relación entre la salida y la tensión de entrada\(V_{out}/V_{in}\).

En el circuito RC, pensado como un divisor de voltaje,

\[gain = \frac{\textrm{capacitive resistance}}{\textrm{total resistance from } V_{in} \textrm{to ground}} = \frac{R_{C}}{R+R_{C}}\]

Porque\(R_{C} = \frac{1}{j \omega C}\), la ganancia se convierte

\[gain = \frac{\frac{1}{j \omega C}}{R + \frac{1}{j \omega C}}\]

Después de borrar las fracciones multiplicando por\(j \omega C\) en el numerador y denominador, la ganancia se simplifica a

\[gain = \frac{1}{1 + j \omega R C}\]

¿Por qué el circuito se llama circuito de paso bajo?

A frecuencias altas (\(\omega\)→ ∞), el\(j \omega R C\) término en el denominador hace que la ganancia sea cero. A bajas frecuencias (\(\omega\)→ 0), el\(j \omega RC\) término desaparece y la ganancia es 1. Las señales de alta frecuencia son atenuadas por el circuito; las señales de baja frecuencia pasan casi sin cambios. Esta descripción abstracta y de alto nivel del circuito nos ayuda a entender el circuito sin que nos entierren en ecuaciones. Pronto trasladaremos nuestra comprensión de este circuito a los sistemas térmicos.

La ganancia contiene los parámetros del circuito como el producto RC. En el denominador de la ganancia,\(j \omega RC\) se suma a 1; por lo tanto\(j \omega RC\), como 1, no debe tener dimensiones. Debido a que j es adimensional (es un número puro),\(\omega RC\) debe ser adimensional en sí mismo. Por lo tanto, el producto RC tiene dimensiones de tiempo. Este producto es la constante de tiempo del circuito, generalmente denotada\(\tau\).

La constante de tiempo tiene dos interpretaciones físicas. Para construirlos, imaginamos cargar el condensador usando un voltaje de entrada constante V ₀; eventualmente (después de un tiempo infinito), el condensador se carga hasta el voltaje de entrada (V _out = V ₀) y mantiene una carga\(Q=CV_{0}\). Entonces, a t = 0, hacemos que el voltaje de entrada sea cero conectando la entrada a tierra.

El condensador se descarga a través de la resistencia, y su voltaje decae exponencialmente:

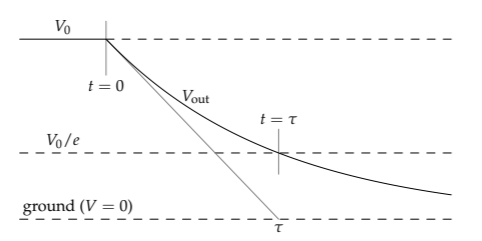
Después de una constante de tiempo\(\tau\), el voltaje del condensador cae en un factor de e hacia su valor final, aquí, de V ₀ a V ₀/e. El tiempo 1/ e es nuestra primera interpretación de la constante de tiempo. Además, si el voltaje del condensador hubiera decaído a su velocidad inicial (justo después de t = 0), habría alcanzado voltaje cero después de una constante de tiempo,\(\tau\) la segunda interpretación de la constante de tiempo.

La abstracción constante de tiempo oculta, abstrae, los detalles que la produjeron: aquí, la resistencia eléctrica y la capacitancia. Los sistemas no eléctricos también pueden tener una constante de tiempo pero producirla por un mecanismo diferente. Nuestra comprensión de alto nivel de las constantes de tiempo, porque no se limita a los sistemas eléctricos, nos ayudará a transferir nuestra comprensión del filtro eléctrico de paso bajo a sistemas no eléctricos. En particular, ahora estamos listos para entender el flujo de calor en los sistemas térmicos.

Ejercicio\(\PageIndex{7}\): Impedance of an inductor

Un inductor tiene la relación voltaje-corriente

\[V = L \frac{dI}{dt}\]

donde L es la inductancia. Encuentre la impedancia ZL dependiente de la frecuencia de un inductor. Después de encontrar esta impedancia, se puede analizar cualquier circuito lineal como si estuviera compuesto solo por resistencias.

2.4.5 Sistemas térmicos

El circuito RC es un modelo para sistemas térmicos, que obviamente no están conectados a circuitos. En un sistema térmico, la diferencia de temperatura, el análogo de diferencia de voltaje, produce una corriente de energía. La corriente energética, en palabras menos elegantes, es el flujo de calor. Además, la corriente es proporcional a la diferencia de temperatura, así como la corriente eléctrica es proporcional a la diferencia de voltaje. En ambos sistemas, el flujo es proporcional al esfuerzo. Por lo tanto, el flujo de calor se puede entender mediante el uso de analogías de circuito.

Como ejemplo, a menudo preparo una taza de té pero me olvido de beberla mientras hace calor. Al igual que un condensador de descarga, el té se enfría lentamente hacia la temperatura ambiente y se vuelve inbebible. El calor fluye a través de la taza. Sus paredes proporcionan una resistencia térmica; por analogía a un circuito RC, denotemos la resistencia térmica R _t. El calor se almacena en el agua y la taza, que forman un depósito de calor. Este reservorio, de calor más que de carga, proporciona la capacitancia térmica, la cual denotamos C _t. (Así la taza participa en la resistencia térmica y capacitancia.) La resistencia y la capacitancia son ideas transferibles.

El producto R _t C _t es, por analogía con el circuito RC, la constante térmica de tiempo\(\tau\). Para estimar\(\tau\) con un experimento casero (el método que utilizamos en la Sección 1.7), calentar una taza de té; a medida que se enfría, dibuja la brecha de temperatura entre el té y la temperatura ambiente. En mi amplia experiencia de abandono del té, una taza de té agradablemente caliente se vuelve tibia en media hora. Para cuantificar estas temperaturas, agradablemente cálido puede ser 130 °F (≈ 55 °C), la temperatura ambiente es 70 °F (≈ 20 °C) y la tibia puede ser 85 °F (≈ 30 °C).

Con base en los datos anteriores, ¿cuál es la constante de tiempo térmica aproximada de la taza de té?

En una constante de tiempo térmica, la brecha de temperatura cae en un factor de e (así como la brecha de voltaje cae por un factor de e en una constante de tiempo eléctrica). Para mi taza de té, la brecha de temperatura entre el té y la habitación comenzó a 60 °F:

\[\underbrace{\textrm{enjoyably warm}}_{130^{o}F} - \underbrace{\textrm{room temperature}}_{70^{o}F} = 60^{o}F.\]

En la media hora mientras el té se enfriaba en el microondas, la brecha de temperatura bajó a 15°F:

\[\underbrace{\textrm{lukewarm}}_{85^{o}F} - \underbrace{\textrm{room temperature}}_{70^{o}F} = 15^{o}F.\]

Por lo tanto, la brecha de temperatura disminuyó en un factor de 4 en media hora. La caída por el factor canónico de e (aproximadamente 2.72) requeriría menos tiempo: quizás 0.3 horas (aproximadamente 20 minutos) en lugar de 0.5 horas. Un cálculo más preciso sería dividir 0.5 horas por ln 4, lo que da 0.36 horas. Sin embargo, tiene poco sentido hacer esta parte del cálculo de manera tan precisa cuando los datos de entrada son mucho menos precisos. Por lo tanto, estimaremos la constante de tiempo térmica\(\tau\) como aproximadamente 0.3 horas.

Usando esta estimación, podemos entender qué le sucede a la taza de té cuando, como suele pasar, unos días solitarios en el microondas, sujeto a las variaciones diarias de la temperatura ambiente. Este análisis se convertirá en nuestro modelo para las variaciones diarias de temperatura en una casa.

¿Cómo responde una taza de té con\(\tau\) ≈ 0.3 horas a las variaciones diarias de temperatura?

Primero, configura la analogía del circuito. La señal de salida sigue siendo la temperatura del té. La señal de entrada es la temperatura ambiente variable (sinusoidalmente). Sin embargo, la señal de tierra, que es nuestra temperatura de referencia, no puede ser también la temperatura ambiente. En cambio, necesitamos una temperatura de referencia constante. La elección más simple es la temperatura ambiente promedio T _avg. (Después de haber transferido este análisis a la variación de temperatura en las casas, veremos que la conclusión es la misma incluso con una temperatura de referencia diferente).

La ganancia conecta las amplitudes de las señales de salida y entrada:

\[gain = \frac{\textrm{amplitude of the output signal}}{\textrm{amplitude of the input signal}} = \frac{1}{1 + j \omega \tau}\]

La señal de entrada (temperatura ambiente) varía con una frecuencia f de 1 ciclo por día. Entonces el parámetro adimensional\(\omega \tau\) en la ganancia es aproximadamente 0.1. Aquí está ese cálculo:

\[\underbrace{2 \pi \times \overbrace{1 \frac{\textrm{cycle}}{\textrm{day}}}^{f}}_{\omega} \times \underbrace{0.3 \textrm{ hr}}_{\tau} \times \underbrace{\frac{1 \textrm{day}}{24 \textrm{hr}}}_{1} \approx 0.1.\]

El sistema es impulsado por una señal de baja frecuencia: no\(\omega\) es lo suficientemente grande como para hacer\(\omega \tau\) comparable a 1. Como nos recuerda la expresión de ganancia, la taza de té es un filtro de paso bajo para variaciones de temperatura. Transmite esta señal de temperatura de entrada de baja frecuencia casi sin cambios a la salida, a la temperatura del té. Por lo tanto, la temperatura interior (té) sigue casi exactamente a la temperatura exterior (ambiente).

El extremo opuesto es una casa. En comparación con la taza, una casa tiene una masa mucho mayor y por lo tanto capacitancia térmica. La constante de tiempo resultante\(\tau = R_{t}C_{t}\) es probablemente mucho más larga para una casa que para la taza. Como ejemplo, cuando enseñé en la soleada Ciudad del Cabo, donde las casas suelen estar sin calefacción incluso en invierno, la casa ligeramente aislada donde me alojé tenía una constante de tiempo térmico de aproximadamente 0.5 días.

Para esta casa el parámetro adimensional\(\omega \tau\) es mucho mayor de lo que era para la taza de té. Aquí está el cálculo correspondiente.

\[\underbrace{2 \pi \times \overbrace{1 \frac{\textrm{cycle}}{\textrm{day}}}^{f}}_{\omega} \times \underbrace{0.5 \textrm{days}}_{\tau} \approx 3.\]

¿Qué consecuencia\(\omega \tau \approx 3\) tiene para la temperatura interior? En el invierno de Ciudad del Cabo, la temperatura exterior varió diariamente entre 45 °F y 75 °F; supongamos también que varió aproximadamente sinusoidalmente. Esta variación pico a pico de 30 °F, después de pasar por el filtro de paso bajo de la casa, se contrae en un factor de aproximadamente 3. Aquí se explica cómo encontrar ese factor estimando la magnitud de la ganancia.

\[|gain| = |\frac{\textrm{amplitude of }T_{inside}}{\textrm{amplitude of } T_{outside}}| = |\frac{1}{1 + j \omega \tau}|\]

(¡Es un poco confuso que la temperatura exterior sea la señal de entrada, y la temperatura interior es la señal de salida!) Ahora conéctelo\(\omega \tau \approx 3\) para obtener

\[|gain| \approx |\frac{1}{1 + 3j}| = \frac{1}{\sqrt{1^{2} + 3^{2}}} \approx \frac{1}{3}\]

En general, cuando\(\omega \tau\) ≫ 1, la magnitud de la ganancia es aproximadamente 1/\(\omega \tau\).

Por lo tanto, la variación exterior pico a pico de 30 °F se convierte en una variación de pico a pico interior más pequeña de 10 °F. Aquí hay un diagrama de bloques que muestra este efecto del filtro de paso bajo de la casa.

Nuestra comodidad depende no sólo de la variación de temperatura (me gusta una temperatura bastante estable), sino también de la temperatura promedio.

¿Cuál es la temperatura promedio en interiores?

¡Resulta que la temperatura promedio en interiores es igual a la temperatura promedio en exteriores! Para ver por qué, pensemos detenidamente en la temperatura de referencia (nuestro análogo térmico de tierra). Antes, en el análisis de la taza de té olvidada, nuestra temperatura de referencia era la temperatura media interior. Debido a que ahora estamos tratando de determinar este valor, usemos una temperatura de referencia conveniente conocida, por ejemplo, la fría 10 °C, que hace que los números redondos sean Celsius o Fahrenheit (50 °F).

La señal de entrada (la temperatura exterior) varió en invierno entre 45° F y 75°F, por lo tanto, tiene dos piezas: (1) nuestra señal variable habitual con la variación pico a pico de 30°F, y (2) una señal constante de 10°F.

La señal constante es la diferencia entre la temperatura exterior promedio de 60°F y la señal de referencia de 50°F.

Vamos a manejar cada pieza a su vez, estamos usando de nuevo el razonamiento de dividir y conquistar. Acabamos de analizar la pieza variable: Pasa por el filtro paso bajo de la casa y, con\(\omega \tau \approx 3\), se contrae significativamente en amplitud. En contraste, la parte no variable, que es la temperatura exterior promedio, tiene frecuencia cero por definición. Por lo tanto, su parámetro adimensional\(\omega \tau\) es exactamente 0. Esta señal pasa a través del filtro de paso bajo de la casa con una ganancia de 1. Como resultado, la señal de salida promedio (la temperatura interior) también es 60°F: la misma señal constante de 10°F medida en relación con la temperatura de referencia de 50°F.

La amplitud de temperatura interna de pico a pico de 10°F es una variación de alrededor de 60°F, por lo tanto, la temperatura interior varía entre 55°F y 65°F (13°C a 18°C). En interiores, cuando no estoy a menudo corriendo o generando mucho calor, me siento cómodo a 68°F (20°C). Entonces, como predice este modelo de circuito de flujo de calor, llevé un suéter día y noche en la casa de Ciudad del Cabo. (Para obtener más información sobre el uso de analogías de circuitos RC para el diseño de edificios, consulte el artículo “Clase maestra de diseño” de Doug King [30].)

Ejercicio\(\PageIndex{8}\): When is the house coldest?

Con base en la forma general para la ganancia,\(1/(1 + j \omega \tau\)), ¿cuándo en el día será la casa de Ciudad del Cabo la más fría, asumiendo que el exterior es más frío a medianoche?