17.2: Posedness Bien

Restringiremos la atención a la estructura de retroalimentación en la Figura 17.5. Nuestra suposición es que\(H_{1}\) y\(H_{2}\) tienen algunas descripciones subyacentes de espacio de estado con entradas\(u_{1}\),\(u_{2}\) y salidas\(y_{1}\)\(y_{2}\), por lo que sus funciones de transferencia\(H_{1}(s)\) y\(H_{2}(s)\) son adecuadas, es decir\(H_{1}(\infty)\),\(H_{2}(\infty)\) son finitas. Es posible (y de hecho típico para modelos de sistemas físicos, ya que su respuesta cae a cero a medida que uno va más alto en frecuencia) que la función de transferencia sea de hecho estrictamente apropiada.

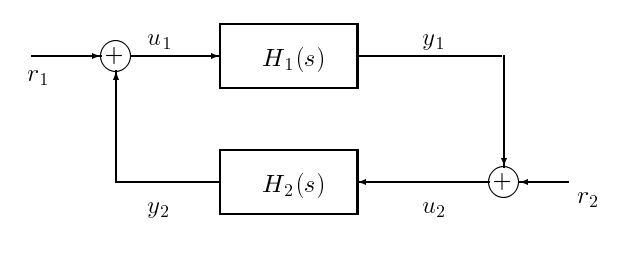
Figura\(\PageIndex{1}\): Interconexión de retroalimentación

El sistema de bucle cerrado en la Figura 17.3.5 se puede describir ahora en forma de espacio de estado escribiendo descripciones de espacio de estado para\(H_{1}(s)\) (con entrada\(u_{1}\) y salida\(y_{1}\)) y\(H_{2}(s)\) (con entrada\(u_{2}\) y salida\(y_{2}\)), y combinándolas de acuerdo con las restricciones de interconexión representado en la Figura 17.3.5. Supongamos que nuestros modelos estado-espacio para\(H_{1}\) y\(H_{2}\) son

\ [H_ {1}\ sim\ left [\ begin {array} {cc}
A_ {1} & B_ {1}\
C_ {1} & D_ {1}
\ end {array}\ derecha],\ quad H_ {2}\ sim\ izquierda [\ begin {array} {cc}
A_ {2} & B_ {2}\
C_ {2} y D_ {2}
\ end {array}\ derecha]\ nonumber\]

con los respectivos vectores de estado, entradas y salidas\(\left(x_{1}, u_{1}, y_{1}\right)\) y\(\left(x_{2}, u_{2}, y_{2}\right)\), entonces

\ [\ begin {alineado}
\ punto {x} _ {1} &=A_ {1} x_ {1} +B_ {1} u_ {1}\\
y_ {1} &=C_ {1} x_ {1} +D_ {1} u_ {1}\
\ punto {x} _ {2} &=A_ {2} x_ {2} ++B_ {2} +B_ {2} +punto {x} _ {2} _ {2}
u_ {2}\\ y_ {2} &=C_ {2} x_ {2} +D_ {2} u_ {2}
\ end {alineado}\\ tag {17.1}\]

Tenga en cuenta que\(D_{1}=H_{1}(\infty)\) y\(D_{2}=H_{2}(\infty)\). Las restricciones de interconexión se plasman en el siguiente conjunto de ecuaciones:

\ [\ begin {array} {l}
u_ {1} =r_ {1} +y_ {2} =r_ {1} +C_ {2} x_ {2} +D_ {2} u_ {2}\\
u_ {2} =r_ {2} +y_ {1} =r_ {2} +C_ {1} x_ {1} +D_ {1} u_ {1},
\ end {array}\ nonumber\]

que se puede reescribir de forma compacta como

\ [\ left [\ begin {array} {cc}
I & -D_ {2}\\
-D_ {1} & I
\ end {array}\ right]\ left [\ begin {array} {l}
u_ {1}\\
u_ {2}
\ end {array}\ right] =\ left [\ begin {array} {cc}
0 & C_ {2}\
C_ {1} & 0
\ end {array}\ right]\ left [\ begin {array} {l}
x_ {1}\\
x_ {2}
\ end {array}\ right] +\ left [\ begin {array} {cc}
I & 0\\
0 & I
\ end {array}\ right]\ left [\ begin {array} {l}
r_ {1}\\
r_ {2}
\ end {array}\ derecha]\\ tag {17.2}\]

Etiquetaremos el sistema interconectado bien planteado si las señales internas del bucle de retroalimentación, es decir,\(u_{1}\) y\(u_{2}\), están definidas de manera única para cada elección de las variables de estado del sistema\(x_{1}\),\(x_{2}\) y entradas externas\(r_{1}\), \(r_{2}\). (Tenga en cuenta que las otras señales internas,\(y_{1}\) y\(y_{2}\), se definirán de manera única bajo estas condiciones si y solo si\(u_{1}\) y\(u_{2}\) son, así que solo nos enfocamos en este último par.) Es evidente a partir de (17.2) que la condición para ello es la invertibilidad de la matriz

\ [\ left [\ begin {array} {cc}
I & -D_ {2}\\
-D_ {1} & I
\ end {array}\ derecha]\ tag {17.3}\]

Esta matriz es invertible si y solo si

\[I-D_{1} D_{2} \text{ or equivalently } I-D_{2} D_{1} \text{ is invertible } \ \tag{17.4}\]

Este resultado se desprende del hecho de que si\(X\)\(Y\),,\(W\) y\(Z\) son matrices de dimensiones compatibles, y\(X\) es invertible entonces

\ [\ nombreoperador {det}\ left [\ begin {array} {cc}
X & Y\\
Z & W
\ end {array}\ derecha] =\ nombreoperador {det} (X)\ nombreoperador {det}\ left (W-Z X^ {-1} Y\ derecha)\ tag {17.5}\]

Una condición suficiente para que (17.4) se mantenga es que cualquiera\(H_{1}\) o\(H_{2}\) (o ambos) sean estrictamente adecuados; es decir, cualquiera\(D_{1} = 0\) o\(D_{2} = 0\).

La significancia del bien posedness es que una vez que hemos resuelto (17.2) determinar\(u_{1}\) y\(u_{2}\) en términos de\(x_{1}\)\(x_{2}\),\(r_{1}\) y\(r_{2}\), podemos eliminar\(u_{1}\) y\(u_{2}\) desde (17.1) y llegar a una descripción estado-espacio del sistema de bucle cerrado, con estado vector

\ [x=\ left (\ begin {array} {l}
x_ {1}\\
x_ {2}
\ end {array}\ derecha)\ nonumber\]

Te dejamos escribir esta descripción explícitamente. Sin bien posedness,\(u_{1}\) y no\(u_{2}\) estaría bien definido para arbitrario\(x_{1}\),\(x_{2}\),\(r_{1}\) y\(r_{2}\), lo que a su vez significaría que no podría haber una representación estado-espacio bien definida del sistema de bucle cerrado.

La condición en (17.4) es equivalente a exigir que

\[\left(I-H_{1}(s) H_{2}(s)\right)^{-1} \text{ or equivalently } \left(I-H_{1}(s) H_{2}(s)\right)^{-1} \text{ exists and is proper } \ \tag{17.6}\]

Ejemplo 17.1

Considere un sistema de tiempo discreto con\(H_{1}(z) = 1\) y\(H_{2}(z) = 1- z^{-1}\) en (la versión DT de) Figura 17.5. En este caso\(\left(1-H_{1}(\infty) H_{2}(\infty)\right)=1-1=0\), y así el sistema está mal planteado. Tenga en cuenta que la función de transferencia de\(r_{1}\) a\(y_{1}\) para este sistema es

\[\left(1-H_{1} H_{2}\right)^{-1} H_{1}=\left(1-1+z^{-1}\right)^{-1}=z\nonumber\]

lo cual no es apropiado - en realidad corresponde a la relación insumo-producto no causal

\[y_{1}(k)=r_{1}(k+1)\nonumber\]

que no puede ser modelada por una descripción estado-espacio.

Ejemplo 17.2

Consideremos nuevamente la Figura 17.4, con\(H_{1}(s)=\frac{s+1}{s+2}\) y\(H_{2}(s)=\frac{s+2}{s+1}\) La expresión\(\left(1-H_{1}(\infty) H_{2}(\infty)\right)=0\), lo que implica que la interconexión está mal planteada. En este caso advertir que,

\ [\ begin {alineado}
\ izquierda (1-H_ {1} (s) H_ {2} (s)\ derecha) &=1-1\\
&=0\ quad\ forall s\ in\ mathbb {C}\!
\ end {alineado}\ nonumber\]

Dado que la inversa de\((1 - H_{1}H_{2})\) no existe, no se pueden anotar las funciones de transferencia que relacionan señales externas con señales internas.