19.2: Representación Multiplicativa de la Incertidumbre

Otro medio sencillo de representar la incertidumbre que tiene algunas propiedades analíticas agradables es la perturbación multiplicativa, que se puede escribir en la forma

\[\Omega_{m}=\left\{P \mid P=P_{0}(1+W \Delta),\|\Delta\|_{\infty} \leq 1\right\}\ \tag{19.5}\]

\(W\)y\(\Delta\) son estables. Al igual que con la representación aditiva, en los conjuntos anteriores se incluyen modelos de orden arbitrariamente grande.

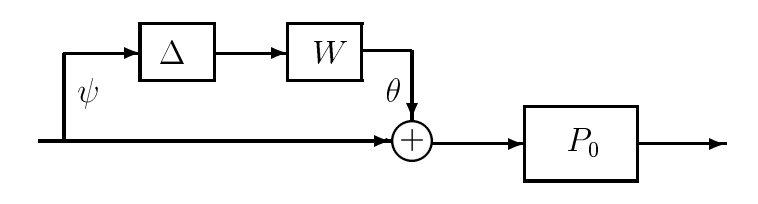
Figura 19.2: Representación de la incertidumbre como perturbación multiplicativa en la entrada de la planta

La precaución mencionada en relación con la perturbación aditiva debe repetirse aquí: las caracterizaciones multiplicativas anteriores no deben interpretarse como diciendo que la planta real es la combinación en cascada del sistema nominal P0 y un sistema\(1 + W \Delta\). Más bien, la planta real debe considerarse como una realización mínima de la función de transferencia\(P (s)\), que pasa a estar escrita en la forma multiplicativa.

Cualquier polo inestable de\(P\) son polos de la planta nominal, pero no necesariamente al revés, porque los polos inestables de\(P_{0}\) pueden ser cancelados por ceros de\(I + W \Delta\). En otras palabras, se permite que la planta real tenga menos polos inestables que la planta nominal, pero todos sus polos inestables están confinados a las mismas ubicaciones que en el modelo nominal. En vista de la cautela del párrafo anterior, tales cancelaciones no corresponden a modos ocultos inestables, por lo que no son motivo de preocupación.

Como en el caso de las perturbaciones aditivas, supongamos que tenemos un conjunto de plantas posibles de\(\Pi\) tal manera que la verdadera planta es miembro de ese conjunto. Podemos intentar incrustar este conjunto en una estructura de perturbación multiplicativa. Primero deje entrar\(P_{0} \in \Pi\) una determinada planta nominal\(\Pi\). Para cualquier otra planta\(P \in \Pi\) tenemos

\[P(j \omega)=P_{0}(j \omega)(1+W(j \omega) \Delta(j \omega))\nonumber\]

El peso\(|W(j \omega)|\) satisface

\ [\ begin {alineado}
|W (j\ omega) | &\ Geq|W (j\ omega)\ Delta (j\ omega) |=\ izquierda|\ frac {P (j\ omega) -P_ {0} (j\ omega)} {P_ {0} (j\ omega)}\ derecha|\\
|W (j\ omega) | &\ geq max\ _ {P\ in\ Pi}\ izquierda|\ frac {P (j\ omega) -P_ {0} (j\ omega)} {P_ {0} (j\ omega)}\ derecha|=\ ell_ {m} (j\ omega)
\ fin {alineado}\ nonumber\]

Con el conocimiento de la envolvente\(l_{m}(j \omega)\), encontramos un sistema estable\(W(s)\) tal que\(|W(j \omega)| \geq l_{m} (j \omega)\)

Ejemplo 19.1 Ganancia incierta

Supongamos que tenemos una planta\(P=k \bar{P}(s)\) con una ganancia incierta\(k\) que se encuentra en el intervalo\(k_{1} \leq k \leq k_{2}\). Podemos escribir de\(k=\alpha(1+\beta x)\) tal manera que

\ [\ begin {array} {l}
k_ {1} =\ alpha (1-\ beta)\\
k_ {2} =\ alpha (1+\ beta)
\ end {array}\ nonumber\]

Por lo tanto\(\alpha=\frac{k_{1}+k_{2}}{2}\)\(\beta=\frac{k_{2}-k_{1}}{k_{2}+k_{1}}\),, y podemos expresar el conjunto de plantas como

\[\Pi=\left\{P(s) \mid P(s)=\frac{k_{1}+k_{2}}{2} \bar{P}(s)\left(1+\frac{k_{2}-k_{1}}{k_{2}+k_{1}} x\right),-1 \leq x \leq 1\right\}\nonumber\]

Podemos incrustar esto\(\Pi\) en una estructura multiplicativa ampliando los elementos inciertos\(x\) que son números reales a complejos\(\Delta(j \omega)\) que representan perturbaciones dinámicas. Esto da como resultado el siguiente conjunto

\[\Omega_{m}=\left\{P(s) \mid P(s)=\frac{k_{1}+k_{2}}{2} \bar{P}(s)\left(1+\frac{k_{2}-k_{1}}{k_{2}+k_{1}} \Delta\right),\|\Delta\|_{\infty} \leq 1\right\}\nonumber\]

Obsérvese que en esta representación\(P_{0}=\frac{k_{1}+k_{2}}{2} \bar{P}\), y\(W=\frac{k_{2}-k_{1}}{k_{2}+k_{1}}\)

Ejemplo 19.2 Retraso incierto

Supongamos que tenemos una planta\(P=e^{-k s} P_{0}(s)\) con un retraso incierto\(0 \leq k \leq k_{1}\). Queremos representar a esta familia de plantas en una estructura de perturbación multiplicativa. El peso\(W(s)\) debe satisfacer

\ [\ begin {alineado}
|W (j\ omega) | &\ geq\ max _ {0\ leq k\ leq k_ {1}}\ izquierda|\ frac {e^ {-j\ omega k} P_ {0} (j\ omega) -P_ {0} (j\ omega)} {P_ {0} (j\ omega)}\ derecha|\\
=\ max _ {0\ leq k\ leq k_ {1}}\ izquierda|e^ {-j\ omega k} -1\ derecha|\\
&=\ izquierda\ {\ comenzar {matriz} {cc}
\ mid 1-e^ {-j\ omega k_ {1}\ mid} &\ omega<\ frac {\ pi} {k_ {1}}\\
0 &\ omega\ geq\ frac {\ pi} {k_ {1}}
\ end {array}\ right. \\
&=\ ell_ {m} (\ omega)
\ final {alineado}\ nonumber\]

Un peso estable que satisfaga la relación anterior se puede tomar como

\[W(s)=\alpha \frac{2 \pi k_{1} s}{\pi k_{1} s+1}\nonumber\]

donde\(\alpha > 1\). El lector debe verificar que este peso va a funcionar trazando\(|W(j \omega)|\) y\(l_{m}( \omega)\), y mostrando que\(l_{m}( \omega)\) está por debajo de la curva\(|W(j \omega)|\) para todos\(\omega\).