19.3: El Criterio Nyquist

Última actualización
Guardar como PDF

Page ID: 85736

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Antes de analizar la estabilidad de los bucles de retroalimentación donde la planta es incierta, revisaremos el criterio Nyquist. Considere la estructura de retroalimentación en la Figura 19.3. La función de transferencia

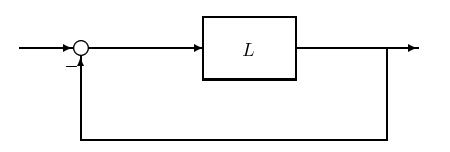
Screen Shot 2020-08-04 a las 5.28.13 PM.png

Figura 19.3: Confuguración de retroalimentación de unidad.

\(L\)se llama la función de transferencia de bucle abierto. La condición para la estabilidad del sistema en 19.3 se asegura si los ceros de\(1 + L\) están todos en la mitad izquierda del plano complejo. El principio argumental a partir del análisis complejo da un criterio para calcular la diferencia entre el número de ceros y el número de polos de una función analítica en un dominio determinado,\(\mathcal{D}\) en el plano complejo. Supongamos que el dominio es como se muestra en la Figura 19.4, y el límite de\(\mathcal{D}\), denotado por\(\delta \mathcal{D}\), está orientado en sentido horario. A esto lo llamamos límite orientado\(\mathcal{D}\) del contorno Nyquist.

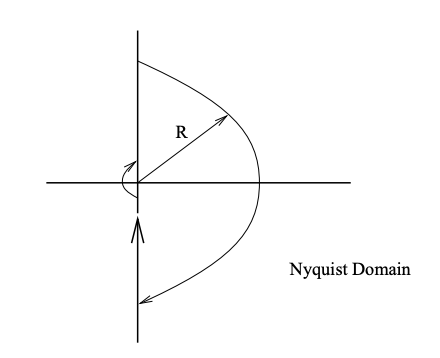
Screen Shot 2020-08-04 a las 5.27.45 PM.png

Figura 19.4: Dominio Nyquist.

A medida que el radio del semicírculo en la Figura 19.4 va al infinito, el dominio cubre la mitad derecha del plano complejo. La imagen de\(\delta \mathcal{D}\) debajo\(L\) se llama parcela Nyquist, ver Figura 19.5. Tenga en cuenta que si\(L\) tiene polos en el\( j \omega\) eje entonces sangramos el contorno Nyquist para evitar estos polos, como se muestra en la Figura 19.4. Definir

\[\pi_{ol} = \text { Open- loop poles = Number of ploes of L in D = Number of poles of 1 + L in D }\nonumber\]

\[\pi_{el} = \text { Closed- loop poles = Number of zeros of 1 + L in D }\nonumber\]

Del principio argumentativo se deduce que

\[\pi_{el} - \pi_{ol}= \text { The number of clockwise encirclements that the Nyquist Plot makes of the point} -1. \nonumber\]

Mediante esta caracterización de la diferencia del número de polos de bucle cerrado y de los polos de bucle abierto se llega al siguiente teorema para la estabilidad de la Figura 19.3

Teorema 19.1

El sistema de bucle cerrado en la Figura 19.3 es estable si y solo si la gráfica Nyquist

no pasa por el origen,
hace\(\pi_{ol}\) cercos en sentido antihorario de\(-1\).