2.2: Sistemas invariantes en el tiempo

Un sistema dinámico es invariable en el tiempo si cambiar la entrada en el eje de tiempo conduce a un desplazamiento equivalente de la salida a lo largo del eje de tiempo, sin otros cambios. En otras palabras, un sistema invariable en el tiempo mapea una trayectoria de entrada dada\(u(t)\) sin importar cuándo ocurra:

\[y(t - \tau) = F[u(t - \tau)] \]

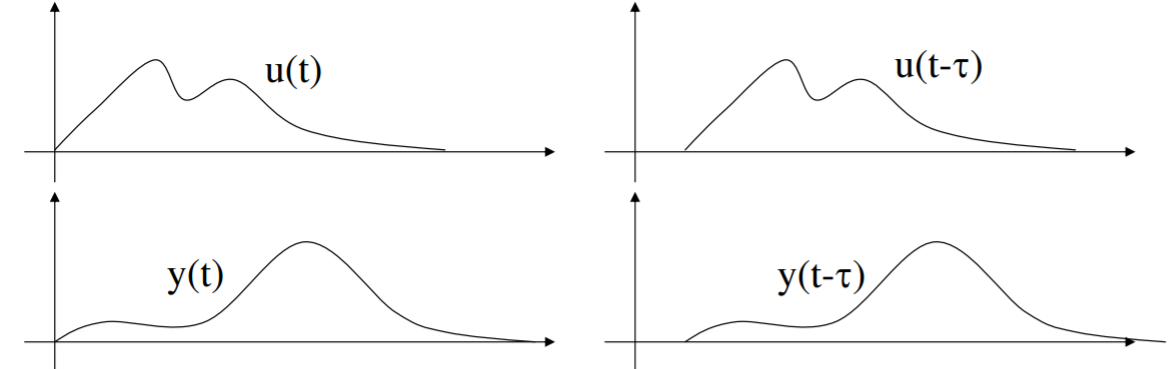
La fórmula anterior dice específicamente que si una señal de entrada se retrasa en alguna cantidad\(\tau\), así será la salida, y sin otros cambios.

Figura\(\PageIndex{1}\): Gráficas de dos sistemas físicos invariantes en el tiempo,\(u(t)\) y\(y(t)\). La forma de cada gráfica no cambia si la señal de entrada se retrasa en alguna cantidad\(\tau\), sino que simplemente se traduce a la derecha por\(\tau\) unidades.

Un ejemplo de un sistema físico variable en el tiempo es la respuesta de cabeceo de un cohete\(y(t)\),, cuando los propulsores están siendo dirigidos por un ángulo\(u(t)\). Se puede ver primero que se trata de un problema de péndulo invertido, e inestable sin un controlador de bucle cerrado. Es variable en el tiempo porque a medida que el cohete quema combustible su masa está cambiando, y así el tono responde de manera diferente a diversas entradas a lo largo de su vuelo. En este caso la coordenada de “tiempo absoluto” es el tiempo desde el despegue.

Para evaluar si un sistema varía en el tiempo o no, siga estos pasos: reemplace\(u(t)\) con\(u(t − \tau)\) en un lado de la ecuación, reemplace\(y(t)\) con\(y(t − \tau)\) en el otro lado de la ecuación y luego verifique si son iguales. Aquí hay varios ejemplos.

\[y(t) = u(t)^{3/2}\]

Este sistema es claramente invariable en el tiempo, porque es un mapa estático. Siguiente ejemplo:

\[y(t) = \int\limits_{0}^{t} \sqrt{u(t_1)}\, dt_1\]

\(u(t_1)\)Reemplázalo por\(u(t_1 - \tau)\) en el lado derecho y llévala a través de:

\[\int\limits_{0}^{t} \sqrt{u(t_1 - \tau)}\, dt_1 = \int\limits_{- \tau}^{t - \tau} \sqrt{u(t_2)}\, dt_2 \nonumber\]

El lado izquierdo es simplemente

\[y(t - \tau) = \int\limits_{0}^{t - \tau} \sqrt{u(t_1)}\, dt_1 \nonumber\]

Claramente los lados derecho e izquierdo no son iguales (los límites de integración son diferentes), y por lo tanto el sistema no es invariable en el tiempo. Como otro ejemplo, considere

\[y(t) = \int\limits_{t-5}^{t} u^2(t_1)\, dt_1 \]

El lado derecho se convierte, con el cambio de tiempo,

\[\int\limits_{t-5}^{t} u^2(t_1 - \tau)\, dt_1 = \int\limits_{t-5-\tau}^{t-\tau} u^2(t_2)\, dt_2 \nonumber \]

mientras que el lado izquierdo es

\[y(t - \tau) = \int\limits_{t-5-\tau}^{t-\tau} u^2(t_1)\, dt_1 \nonumber \]

Los dos lados de la ecuación definitoria son iguales bajo un cambio de tiempo\(\tau\), por lo que este sistema es invariable en el tiempo. Aquí se encuentra una sutileza al considerar entradas que son cero antes del tiempo cero - esta es la suposición habitual en nuestro trabajo, es decir,\(u(t) = 0\) para\(t \leq 0\). Si bien la linealidad no se ve afectada por esta condición, la invarianza de tiempo lo es, porque la suposición es inconsistente con el avance de una señal en el tiempo. ¡Claramente parte de la entrada estaría truncada! Restringiendo nuestra discusión a los retardos de señal (la\(- \tau\) inserción de en el argumento, donde estrictamente\(\tau > 0\)) resuelve el problema y preserva la invarianza de tiempo según sea necesario.