11.4: Representando Sistemas Lineales

La descripción de la función de transferencia de sistemas lineales ya ha sido descrita en la presentación de la transformada de Laplace. La forma de espacio de estado es una representación de dominio de tiempo completamente equivalente que hace una extensión limpia a los sistemas con múltiples entradas y múltiples salidas, y abre el camino a muchas herramientas estándar del álgebra lineal.

Formulario estándar de espacio de estado

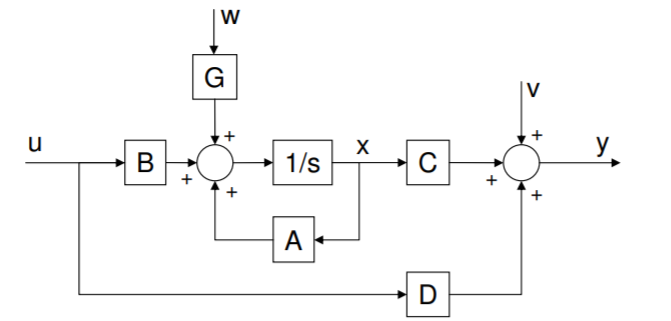
Escribimos un sistema lineal en forma estado-espacio de la siguiente manera

\ begin {align}\ punto {x}\,\, &=\,\, Ax + Bu + Gw\\ [4pt] y\,\, &=\,\, Cx + Du + v\ end {align}

donde

• \(x\)es un vector de estado, con tantos elementos como órdenes haya en las ecuaciones diferenciales gobernantes.
• \(A\)es una matriz\(x\) que mapea a su derivada;\(A\) captura la dinámica natural del sistema sin entradas externas.
• \(B\)es una matriz de ganancia de entrada para la entrada de control\(u\).
• \(G\)es una matriz de ganancia para perturbaciones desconocidas\(w\);\(w\) impulsa el estado al igual que el control\(u\).
• \(y\)es el vector de observación, compuesto principalmente por una combinación lineal de estados\(Cx\) (donde\(C\) es una matriz).
• \(Du\)es un mapa directo de entrada a salida (generalmente cero para sistemas físicos).
• \(v\)es un ruido de sensor desconocido que corrompe la medición.

Figura\(\PageIndex{1}\): diagrama de bloques ilustra la relación entre las diferentes variables introducidas en Ecuaciones\(\PageIndex{1}\) -\(\PageIndex{2}\).

Conversión de un modelo estado-espacio en una función de transferencia

Muchas descripciones de espacio de estado diferentes pueden crear la misma función de transferencia; no son únicas. En el caso de que no haya perturbaciones o ruido, la función de transferencia se puede escribir como

\[ P(s) \, = \, \frac{y(s)}{u(s)} \, = \, C(sI - A)^{-1} B + D,\]

donde\(I\) está la matriz de identidad con el mismo tamaño que\(A\). Para ver que esto es cierto, simplemente transforma la ecuación diferencial en espacio de frecuencia:

\ begin {alinear*} sx (s)\,\, &=\,\, Ax (s) + Bu (s)\ largoderrow\\ [4pt] x (s) (Si - A)\,\, &=\,\, Bu (s)\ largoderrow\ [4pt] x (s)\,\, &=\,\, (Si - A) ^ {-1} Bu (s)\ largofila derecha\\ [4pt] y (s)\,\, &=\,\, Cx (s) + Du (s)\,\, =\,\, C (Si - A) ^ {-1} Bu (s) + Du (s). \ end {alinear*}

Una ecuación similar se mantiene para\(y(s)/w(s)\), y claramente\(y(s)/v(s) = 1\).

Conversión de una función de transferencia en un modelo estado-espacio

Debido a que los modelos estado-espacio no son únicos, hay muchas formas diferentes de crearlos a partir de una función de transferencia. En el caso más simple, puede ser posible escribir la ecuación diferencial correspondiente a lo largo de una fila del vector de estado, y luego derivaciones en cascada. Por ejemplo, considere el siguiente sistema:

\ begin {align*} my "(t) + por' (t) + ky (t)\,\, &=\,\, u' (t) + u (t) &\ text {(masa-primavera-dashpot)}\\ [4pt] P (s)\,\, &=\,\,\ frac {s+1} {ms^2 + bs + k}\ end align{ *}

Ajuste\(\vec{x} = [y', \, y]^T\), obtenemos el sistema

\ begin {align*}\ dfrac {d\ vec {x}} {dt}\,\, &=\,\,\ begin {bmatrix} -b/m & -k/m\\ [4pt] 1 & 0\ end {bmatrix}\ vec {x} +\ begin {bmatrix} 1/m\\ [4pt] 0\ end {bmatrix} u\ [4pt]] y\,\, &=\,\, [1\ quad 1]\ vec {x}\ end {alinear*}

Tenga en cuenta específicamente que\(dx_2 / dt = x_1\), lo que lleva a una entrada de\(1\) en el fuera de la diagonal de la segunda fila en\(A\). Las entradas en la\(C\) matriz -son fáciles de escribir en este caso debido a la linealidad; la respuesta del sistema a\(u'\) es la misma que la derivada de la respuesta del sistema a\(u\).