16.3: Producto Dot

Última actualización
Guardar como PDF

Page ID: 84059

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El producto punto (también llamado a veces el producto escalar) es una operación matemática que se puede realizar en dos vectores cualesquiera con el mismo número de elementos. El resultado es un número escalar igual a la magnitud del primer vector, multiplicado por la magnitud del segundo vector, multiplicado por el coseno del ángulo entre los dos vectores.

\[ \vec{A} \cdot \vec{B} = |A| |B| \cos (\theta) \]

En mecánica de ingeniería, el producto punto se utiliza casi exclusivamente con un segundo vector que es un vector unitario. Si el segundo vector en la operación de producto de punto es un vector unitario (teniendo así una magnitud de 1), el producto de punto representará entonces la magnitud del primer vector en la dirección del vector unitario. En este sentido, un producto de punto es útil para determinar el componente de un vector dado en cualquier dirección dada, donde la dirección se da en términos de un vector unitario.

El vector A apunta bruscamente hacia arriba y hacia la derecha. Un vector B más corto se origina en el mismo punto que A, apuntando menos bruscamente hacia arriba y hacia la derecha. Los dos vectores crean un ángulo de theta entre ellos. Un tercer vector C, dibujado como una línea punteada, apunta a lo largo de B y lo extiende para formar una pata de un triángulo rectángulo con el vector A como hipotenusa. C representa el producto punteado de A y B, que es el producto de las longitudes de A y B con cos (theta). Si B es un vector unitario con magnitud 1, el producto de punto es simplemente la magnitud de A veces cos (theta). — Figura\(\PageIndex{1}\): El producto de punto de un vector con un vector unitario le dará la magnitud del primer vector en la dirección del vector unitario.

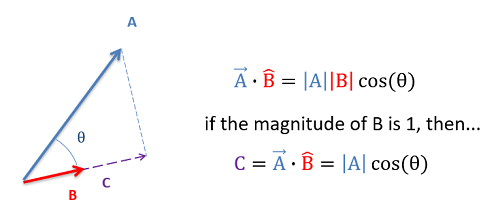
Como alternativa a la ecuación anterior para calcular el producto punto, también podemos calcular el producto punto sin conocer el ángulo entre los vectores (\(\theta\)). Para este método, dividimos cada vector en componentes y tomamos la suma de cada conjunto de componentes multiplicados juntos como se muestra en la siguiente ecuación.

\[ \vec{A} \cdot \vec{B} = (A_x * B_x) + (A_y * B_y) + (A_z * B_z) \]

Por último, como ocurre con muchas operaciones vectoriales, la verdadera fuerza del producto punto es que las computadoras pueden calcularlas muy rápidamente. Tanto MATLAB como Wolfram Alpha Vector Operation Calculator son capaces de calcular productos de punto para usted.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/-MMHU4UhutQ.

Ejemplo\(\PageIndex{1}\)

Encuentra el producto de punto del vector de fuerza\(\vec{A}\) con el vector de unidad dado\(\hat{B}\).

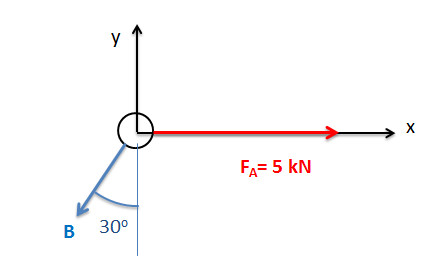
Plano de coordenadas cartesianas bidimensionales de orientación estándar con dos vectores que irradian desde el origen. El vector A tiene una magnitud de 5 kN y apunta en la dirección x positiva. El vector B, un vector unitario, apunta 30° en sentido horario desde la dirección y negativa. — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un vector de fuerza y un vector unitario irradian desde el origen de un sistema de coordenadas cartesianas bidimensionales.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/JJ3aXtIZwZ0.

Ejemplo\(\PageIndex{2}\)

Calcular el producto punto de\(\vec{A}\) con\(\vec{B}\) a mano.

El vector A tiene componentes x, y, z [1, 3, 5]. El vector B tiene componentes x, y, z [6, 4, 2]. Encuentra su producto punto. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\).

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/NuuYcDNeja4.

Ejemplo\(\PageIndex{3}\)

Calcular el producto punto de\(\vec{A}\) con\(\vec{B}\) usando MATLAB.

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/B8PKJtL63C0.

Ejemplo\(\PageIndex{4}\)

Calcule el producto puntual de\(\vec{A}\) con\(\vec{B}\) usando la Calculadora de Operación Vector Wolfram.

Solución:: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/2FZSXFASFiQ.