1.7: Ancho de Agotamiento
- Page ID
- 86356
Ahora podemos volver a la densidad de carga en función del gráfico de posición y encontrar fácilmente el campo eléctrico en la región de agotamiento en función de la posición. Si integramos la Ley de Gauss, obtenemos para el campo eléctrico: \[\mathbf{E} (x) = \frac{1}{\varepsilon} \int \rho(x) \ dx \nonumber \]
Podríamos escribir una expresión para\(\rho(x)\) y luego integrarla formalmente para obtener\(\mathbf{E} (x)\) pero también podemos simplemente hacerlo gráficamente, lo cual es mucho más fácil, y nos da una sensación mucho más intuitiva de lo que está pasando. Empecemos a hacer nuestra integral en\(x \rightarrow \infty\). Siempre que realizamos una integral como Ecuación\(\PageIndex{1}\), tenemos que recordar agregar una constante a nuestra respuesta. Como no podemos tener un campo eléctrico que se extienda hasta el infinito (ya sea más o menos), sin embargo, podemos asumir con seguridad\(\mathbf{E} (- \infty)\) y permanecer en ese valor hasta llegar al borde de la región de agotamiento en (esencialmente)\(x=0\). Dado que la densidad de carga es cero hasta el borde de la región de agotamiento, Gauss nos dice que el campo eléctrico tampoco puede cambiar aquí. Cuando llegamos a\(x=0\) nos encontramos con la gran función delta negativa de carga negativa en el borde de la región de agotamiento. Si puedes recordar de nuevo a tu cálculo, cuando integras una función delta, obtienes un paso. Dado que la carga en la función delta del lado p es negativa, cuando la integramos, obtenemos un paso negativo. Como no sabemos (todavía) qué tan grande será el paso, solo llamémoslo\(- \left| E_{\max} \right|\).
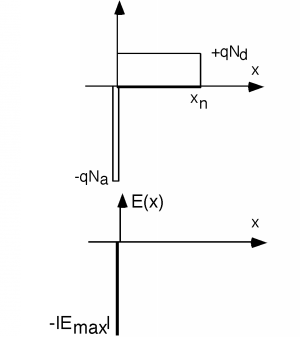
En el lado n de la región de agotamiento,\[\begin{array}{l} \rho(x) &= (q) N_{d} \\ &= \varepsilon \dfrac{\delta \mathbf{E}}{\delta x} \end{array} \nonumber \]
y así trazamos\(\mathbf{E}(x)\) con una pendiente (positiva) de\(\frac{q N_{d}}{\varepsilon}\) comenzar\(E(x) = - E_{\max}\) a las\(x=0\). Esta línea continúa con esta pendiente positiva hasta alcanzar un valor de\(0\) at\(x_{n}\). Sabemos que\(E(x)\) debe igualar\(0\) en\(x = x_{n}\) porque no hay más cargos fuera de la región de agotamiento y\(E\) debe estar\(0\) fuera de esta región.
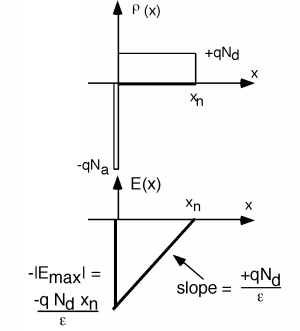
Ya terminamos de hacer lo integral. Sabríamos todo sobre este problema, si supiéramos lo que\(x_{n}\) era. Tenga en cuenta que como conocemos la pendiente del triángulo ahora, podemos encontrar\(-E_{\max}\) en cuanto a la pendiente y\(x_{n}\). Podemos derivar una expresión para\(x_{n}\), si recordamos que la integral del campo eléctrico a lo largo de una distancia es la caída potencial a través de esa distancia. ¿Cuál es la caída de potencial al pasar del lado p al lado n del diodo?
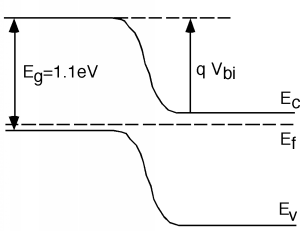
Como recordatorio, la Figura\(\PageIndex{3}\) muestra nuevamente el diagrama de bandas de cruce. La caída de potencial solo debe ser\(V_{\mathrm{bi}}\), el potencial “incorporado” del cruce. Obviamente no\(V_{\mathrm{bi}}\) puede ser mayor que\(1.1 \mathrm{~V}\), el potencial band-gap. Por otro lado, al mirar Figura\(\PageIndex{3}\), y recordando que la banda gap en silicio es\(1.1 \mathrm{~eV}\), tampoco será algún valor como 0.2 o 0.4 voltios. Hagamos la vida más fácil para nosotros mismos, y digamos\(V_{\mathrm{bi}} = 1 \mathrm{~Volt}\). Esto no va a estar muy lejos, y como verás en breve, la respuesta no es muy sensible al valor exacto de\(V_{\mathrm{bi}}\) todos modos.
La integral de\(\mathbf{E}_{x}\) es ahora solo el área del triángulo en la Figura\(\PageIndex{2}\). Conseguir el área es fácil:\[\begin{array}{l} \text{area} &= \frac{1}{2} \text{ base} \times \text{height} \\ &= \frac{1}{2} \ x_{n} \frac{q N_{d} x_{n}}{\varepsilon} \\ &= \frac{q N_{d} x_{n}^2}{2 \varepsilon} \\ &= V_{\mathrm{bi}} \end{array} \nonumber \]
Simplemente podemos darle la\(\PageIndex{3}\) vuelta a Ecuación y resolver por\(x_{n}\). \[x_{n} = \sqrt{ \frac{2 \varepsilon V_{\mathrm{bi}}}{q N_{d}} } \nonumber \]
Como decíamos, para el silicio,\(\varepsilon_{\mathrm{Si}} = 1.1 \times 10^{-12}\). Vamos a dejar a\(N_{d} = 10^{16} \mathrm{~cm}^{-3}\) los donantes. Como ya sabemos de antes,\(q = 1.6 \times 10^{-19} \mathrm{~Coulombs}\). Esto hace\(x_{n} = 3.7 \times 10^{-5} \mathrm{~cm}\) o\(0.37 \ \mu \mathrm{m}\) largo. ¡No es una región de agotamiento muy amplia! ¿Qué tan grande es\(\left| E_{\max} \right|\)? Conectando\[E_{\max} = \frac{q N_{d} x_{n}}{\varepsilon} \nonumber \]
¡nos encontramos con eso\(\left| E_{\max} \right| = 53,000 \ \frac{\mathrm{V}}{\mathrm{cm}}\)! ¿Por qué un campo eléctrico tan grande? Bueno, tenemos que cambiar el potencial en aproximadamente un voltio, y no tenemos mucha distancia para hacerlo en (menos de una micra), y así debe haber, por defecto, un campo bastante grande en la región de agotamiento. Recuerde, el potencial es el campo eléctrico tiempos distancia.
Suficiente electrostática de unión p-n. El punto de este ejercicio era doble; así sabrías algo sobre los detalles de lo que realmente está pasando en un cruce p-n para mostrarte que con solo algunas electrostáticas muy simples y un poco de pensamiento, ¡no es tan difícil resolver estas cosas!


