3.10: Lógica CMOS

Última actualización
Guardar como PDF

Page ID: 86390

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figura\(\PageIndex{1}\): Un transistor PMOS

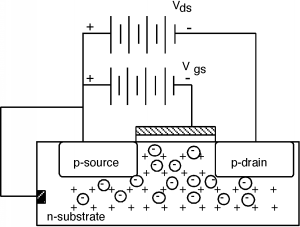
Un bloque de silicio tipo n tiene dos regiones de tipo p en su cara superior. El de la izquierda es el p-source, y el de la derecha es el p-drain. La fuente está conectada al sustrato n, al extremo positivo de una fuente de voltaje V_ds cuyo otro extremo está conectado al drenaje, y al extremo positivo de una fuente de voltaje V_gs cuyo otro extremo está conectado al canal entre la fuente y el drenaje. — Figura\(\PageIndex{1}\): Un transistor PMOS

Esto se parece mucho a nuestro MOSFET anterior excepto que ahora tenemos un sustrato tipo n y las regiones de origen y drenaje son de tipo p. Si aplicamos un negativo\(V_{\text{gs}}\) (con la fuente conectada al sustrato tipo n) entonces la carga negativa inducida en la puerta alejará los electrones, y si las bandas debajo de la puerta están suficientemente dobladas hacia arriba, forman una capa de inversión de agujeros (ver Figura\(\PageIndex{2}\), así hacer un MOSFET de canal p en modo de mejora o un transistor PMOS. (A diferencia de un transistor NMOS que estudiamos primero.). Tenga en cuenta que un transistor PMOS tendrá un negativo\(V_{T}\). Es decir, el voltaje de puerta tiene que ser menor que el voltaje de fuente/sustrato para encender el dispositivo. Cuanto más negativo\(V_{\text{gs}}\) es, más corriente tendremos fluyendo a través del dispositivo.

Figura\(\PageIndex{2}\): Inversión de una capa de tipo n

Diagramas de banda para una capa de tipo n invertida. Las bandas de conductancia y cenefa se inclinan bruscamente en el borde izquierdo de la gráfica, antes de nivelarse con la banda de conductancia cercana a e_F y la banda de cenefa muy por debajo de ella. — Figura\(\PageIndex{2}\): Inversión de una capa de tipo n

Resulta que una combinación tanto de un dispositivo de canal n como de canal p en el mismo circuito puede ser muy ventajosa. Dicha tecnología se llama CMOS, por “MOS complementarios”. Así es como usamos un transistor de canal p en el circuito inversor.

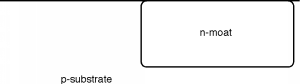
En primer lugar, sin embargo, tenemos que ver cómo haríamos uno. Existe un problema fundamental al tratar de usar dispositivos tanto de canal n como de canal p en el mismo circuito. ¿Qué es? Parecería que necesitamos dos tipos diferentes de sustratos, tanto un sustrato tipo p para el transistor de canal n como un sustrato tipo n para el dispositivo de canal p. Hay una forma de evitar este problema haciendo lo que se llama un tanque o un foso. Un foso es una región relativamente profunda de un tipo de material colocado en un sustrato huésped del tipo opuesto (Figura\(\PageIndex{3}\)). Podemos poner regiones de fuente/drenaje de tipo n en el sustrato p y regiones de fuente/drenaje tipo p en el foso n. En la Figura\(\PageIndex{4}\), también mostraremos las puertas, y cómo todo el inversor está conectado entre sí.

Figura\(\PageIndex{3}\): Preparación para un inversor CMOS

Vista en primer plano de un sustrato p que contiene una región de tipo n pequeña pero relativamente profunda en su parte superior, etiquetada como el foso n. — Figura\(\PageIndex{3}\): Preparación para un inversor CMOS

Figura\(\PageIndex{4}\): Un inversor CMOS

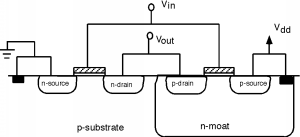
Un sustrato p, con una fuente n y un drenaje n, contiene un foso n que tiene un drenaje p y una fuente p. El canal entre la fuente de tipo n y el drenaje está conectado al canal entre la fuente tipo p y el drenaje, y se aplica un voltaje V_in a ambos. El n-drain y el p-drain están conectados, y se lee un voltaje V_out de la conexión. La fuente n está conectada al sustrato p y a tierra. La fuente p está conectada al foso n, y el voltaje leído de esta conexión es V_dd. — Figura\(\PageIndex{4}\): Un inversor CMOS

Ahora dibujemos el esquema: Un dispositivo de canal p se dibuja igual que un dispositivo de n canales, excepto que ponemos una pequeña “burbuja” en la puerta para significar que es un MOSFET de un color diferente. Aunque normalmente no hacemos esto todo el tiempo, también hemos mostrado las conexiones de sustrato en este diagrama. Estas conexiones muestran que un MOSFET es al menos un dispositivo de cuatro terminales, no uno de tres terminales como suele suponer la gente. Dado que, en un dispositivo de canal p, el sustrato es de tipo n, mostramos la conexión del sustrato como una flecha que apunta hacia afuera. El sustrato tipo p para el dispositivo de canal n se muestra como una flecha que apunta hacia adentro. El sustrato de canal n está conectado a tierra, y el sustrato de canal p está conectado a\(V_{\text{dd}}\). Tenga en cuenta que dado que el foso n está en\(V_{\text{dd}}\) y el sustrato p está en el suelo, la unión p-n de sustrato de foso es de polarización inversa, por lo que no debe fluir corriente entre ellos.

Figura\(\PageIndex{5}\): Esquema de un inversor CMOS

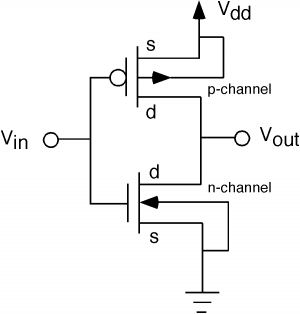
Se aplica un voltaje V_in a la conexión entre las puertas de dos MOSFET, con la superior mostrando el n-drenaje y la fuente n en un sustrato p y la inferior mostrando la fuente p y el p-drenaje en un foso n. Los drenajes de los dos MOSFET están conectados, y se lee un voltaje V_out de esta conexión. La fuente n está conectada a tierra y la fuente p está en voltaje V_dd. Hay una flecha que apunta hacia afuera que conecta el canal p a V_dd, y una flecha que apunta hacia adentro que conecta el suelo con el canal n. — Figura\(\PageIndex{5}\): Esquema de un inversor CMOS

Por lo general, tampoco etiquetamos la fuente y drenamos, pero lo hacemos aquí, solo por completitud. Tenga en cuenta que a diferencia del transistor bipolar, el FET es realmente un dispositivo simétrico. Realmente no hay forma de decir la fuente desde el desagüe. Por convención, llamamos al elemento que está conectado al sustrato (o foso) la fuente, y al otro el drenaje. A veces escuchará la región debajo de la puerta (ya sea sustrato o foso) conocida como el backbody.

Ahora veamos cómo funciona este circuito. Si\(V_{\text{in}}\) es alto (en o cerca\(V_{\text{dd}}\)) el transistor NMOS se encenderá. El voltaje entre la puerta y el sustrato del dispositivo de canal p está en o cerca de cero. ¡La puerta está en\(V_{\text{dd}}\) y también el foso! De ahí que el transistor superior se apagará. La salida será así baja.

Si el voltaje de entrada está en o cerca de tierra (un “bajo”), entonces el dispositivo de canal n se apaga. El voltaje entre la puerta y el sustrato del dispositivo de canal p es ahora\(\simeq \left( -V_{\text{dd}} \right)\). (La puerta es\(\simeq 0\) y el sustrato está en\(V_{\text{dd}}\).) Si el transistor PMOS tiene un voltaje umbral\(V_{T}\) de, digamos\(-2 \mathrm{~V}\),, entonces se encenderá y la salida será alta. Sin embargo, tenga en cuenta que en cualquier estado, alto o bajo, no hay corriente estática que fluya a través del inversor.

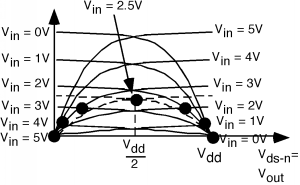
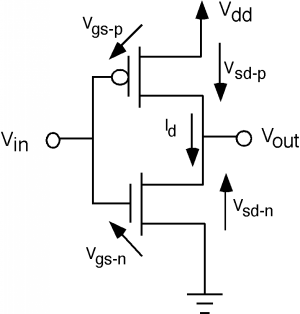
Las características de transferencia para este circuito son un poco más complicadas. Primero, asegurémonos de tener nuestros voltajes y corrientes definidos. De la Figura\(\PageIndex{6}\), el voltaje puerta-fuente de canal n,\(V_{\text{gs-}n}\), es justo\(V_{\text{in}}\). El voltaje puerta-fuente para el dispositivo de canal p,\(V_{\text{gs-}p}\), es\(V_{\text{in}} - V_{\text{dd}\);\(V_{\text{ds-}p}\), el voltaje dreno-fuente para el transistor de canal p se puede escribir como\(V_{\text{ds-}n} - V_{\text{dd}}\). Para corriente,\(I_{d \text{-} n} = I_{d \text{-} p} = I_{d}\). Como se ve en la Figura\(\PageIndex{7}\), tenemos dos conjuntos de curvas características. Tenga en cuenta que desde\(V_{\text{gs-}p} = V_{\text{in}} - V_{\text{dd}}\)\(V_{\text{in}} = 0 \mathrm{~V}\), cuando,\(V_{\text{gs-}p} = -5 \mathrm{~V}\) y así el transistor está fuertemente encendido.

Figura\(\PageIndex{6}\): Definición de voltajes

El inversor CMOS de la Figura 5 anterior tiene V_GS-p definido como el voltaje entre la puerta y la fuente del canal p, V_GS-n definido como el voltaje entre la puerta y la fuente del canal n, V_sd-P definido como el voltaje entre la fuente del canal p y el drenaje, y V_sd-n definido como el voltaje entre el fuente de canal n y drenaje. El I_d actual apunta desde el canal p al canal n, a través de la conexión desde la que se lee V_out. — Figura\(\PageIndex{6}\): Definición de voltajes

Figura\(\PageIndex{7}\): Corrientes de drenaje para los dos transistores en función del voltaje de entrada y\(V_{\text{ds}}\)

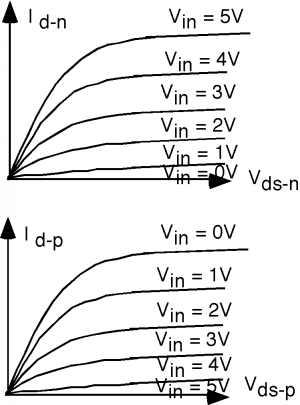
Gráficas de I_d vs V_ds para el dispositivo de canal n, e I_d vs V_ds para el dispositivo de canal p, cada una mostrando 6 curvas características con la curva más baja a lo largo del eje x. Para la gráfica de canal n, la curva más alta tiene V_in de 5 voltios y la menor tiene V_in de 0 V. Para la gráfica de canal p, la curva más alta tiene V_in de 0 V y la menor tiene V_in de 5 V. — Figura\(\PageIndex{7}\): Corrientes de drenaje para los dos transistores en función del voltaje de entrada y\(V_{\text{ds}}\)

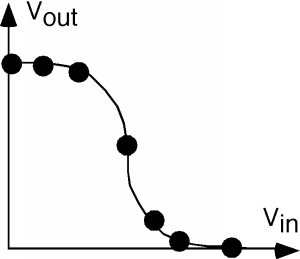
Tenemos una serie de diferentes “líneas de carga” en este caso, porque para cada una\(V_{\text{in}}\) tenemos una curva diferente tanto para los transistores de canal n como p. Esto se muestra en la Figura\(\PageIndex{8}\). Los puntos negros muestran el punto de intersección. Sigue algunas de las curvas a lo largo para ver si estás de acuerdo con dónde se han colocado los puntos. También hemos agregado un par de curvas punteadas para\(V_{\text{in}} = 2.5 \mathrm{~V}\) así poder obtener el punto de “vuelta”. Proyectar la ubicación de los puntos negros al eje\(V_{\text{ds-}n}\) (o\(V_{\text{out}}\)) nos dará un valor\(V_{\text{out}}\) para cada una de las tensiones de entrada,\(V_{\text{in}}\). La curva resultante se muestra en la Figura\(\PageIndex{9}\). Esto nos da una buena “sensación” de cómo funciona el inversor, y cómo varía la salida con la entrada. Tenga en cuenta que esta curva de transferencia es bastante simétrica alrededor de 2.5 voltios, y va desde +5 a 0 voltios en la salida.

Figura\(\PageIndex{8}\): Obtención de la función de transferencia

Las curvas características de canal n de la Figura 7 anterior se superponen con las curvas características de canal p, se reflejan sobre el eje y y se trasladan a la derecha para que intersecten el eje horizontal V_out en el punto V_dd. Estas curvas que se cruzan forman 5 parábolas cóncavas. Las líneas punteadas muestran las curvas de canal n y p para V__= 2.5 voltios, superpuestas de la misma manera; el máximo de la parábola que forman tiene un valor de salida en V de la mitad de V_dd. — Figura\(\PageIndex{8}\): Obtención de la función de transferencia

Figura\(\PageIndex{9}\): Características de transferencia del inversor CMOS

Gráfica de V_out vs V_in, que toma la forma de una curva inverso-S que conecta los 5 V en el eje vertical a los 5 V en el eje horizontal. — Figura\(\PageIndex{9}\): Características de transferencia del inversor CMOS