4.4: Primera Ley de Fick

Última actualización
Guardar como PDF

Page ID: 86514

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

¡CNX se retira! Los libros de texto de OpenStax siempre estarán disponibles en openstax.org. El contenido creado por la comunidad permanecerá disponible hasta agosto de 2022 y luego se trasladará a Internet Archive. Conoce más aquí

Hablamos de difusión en el contexto de diodos, y describimos la Primera Ley de Difusión de Fick para alguna concentración de partículas\(N(x, \ t)\):\[\text{Flux} = (-D) \frac{\text{d} N(x, t)}{\text{d} x} \quad\quad \text{Fick's First Law of Diffusion}\]\(D\) es el coeficiente de difusión y tiene unidades de\(\mathrm{cm} / \mathrm{sec}\).

En un semiconductor, las impurezas se mueven intersticialmente, lo que significa que viajan entre los sitios de celosía (Figura\(\PageIndex{1}\)), o se mueven por difusión por sustitución, lo que significa que saltan de sitio de celosía a sitio de celosía (Figura) \(\PageIndex{2}\)). La difusión por sustitución sólo es posible si la celosía tiene una serie de vacantes, o sitios de celosía vacíos, dispersos por todo el cristal, de manera que haya lugares en los que se pueda mover la impureza. El movimiento intersticial requiere energía para superar la barrera potencial de las regiones entre los sitios de celosía. Se requiere energía para formar las vacantes de difusión sustitutiva. Así, para cualquier forma de difusión, el coeficiente de difusión\(D\), es una fuerte función de la temperatura.

Figura\(\PageIndex{1}\): Difusión intersticial

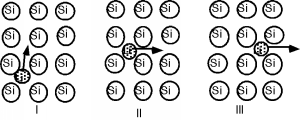
Una rejilla de átomos de silicio tiene una impureza que se mueve a través de los espacios en blanco de la cuadrícula. — Figura\(\PageIndex{1}\): Difusión intersticial

Figura\(\PageIndex{2}\): Difusión sustitucional

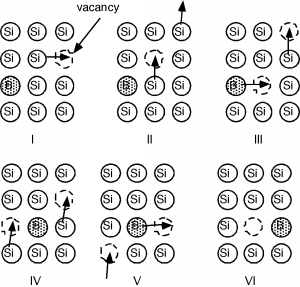
Una cuadrícula mayoritariamente completa de átomos de silicio tiene un punto vacante en la red y otro punto ocupado por boro en lugar de silicio. Un átomo de silicio al lado del lugar vacante se mueve hacia él, abriendo una nueva vacante; el proceso se repite varias veces hasta que se abre una vacante junto al átomo de boro. El átomo de boro se mueve hacia ese lugar vacante, y el proceso se repite para permitir que el boro se difunda a través de la red. — Figura\(\PageIndex{2}\): Difusión sustitucional

Con un muy buen grado de precisión, se puede describir la dependencia de temperatura del coeficiente de difusión con una energía de activación de\(E_{A}\) tal manera que:\[D(T) = D_{o} e^{- \frac{E_{a}}{kT}}\]

La energía de activación\(E_{A}\) y el coeficiente\(D_{o}\) se obtienen de una gráfica del logaritmo natural de\(D\) vs.\(\dfrac{1}{kT}\), denominada gráfica de Arrhenius (Figura\(\PageIndex{3}\)). La pendiente da\(E_{A}\) y la proyección a infinita\(T\)\(\left( \frac{1}{T} \rightarrow 0\right)\) da\(\ln \left(D_{o}\right)\).

Figura\(\PageIndex{3}\): Gráfica de Arrhenius de constante de difusión

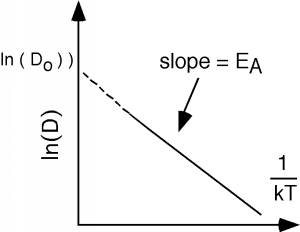
La gráfica del logaritmo natural de D vs el recíproco de kT toma la forma de una línea con una pendiente negativa igual al valor de E_A y una intercepción y igual al logaritmo natural de D_o. — Figura\(\PageIndex{3}\): Gráfica de Arrhenius de constante de difusión

La ecuación de continuidad se mantiene para el movimiento de las impurezas tal como lo hace para cualquier otra cosa, por lo que la divergencia del flujo\(\text{div } (F)\),, debe ser igual al negativo de la tasa de cambio de tiempo de la concentración de las impurezas, o, en una dimensión:\[\frac{\text{d}}{\text{d} x} (\text{Flux}) = - \frac{\text{d} N(x, t)}{\text{d} x}\]