5.3: Ecuación de Línea de Transmisión

Última actualización
Guardar como PDF

Page ID: 86477

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Tenemos que resolver las ecuaciones del telégrafo,\[\frac{\partial V(x, t)}{\partial x} = -\left(\mathbf{L} \frac{\partial I(x, t)}{\partial t}\right)\]\[\frac{\partial (I, t)}{\partial x} = - \left(\mathbf{C} \frac{\partial V(x, t)}{\partial t}\right)\]

La forma en que procederemos a una solución, y la forma en que procedes siempre cuando te enfrentas a un par de ecuaciones como estas, es tomar una derivada espacial de una ecuación, y luego sustituir la segunda ecuación por la derivada espacial en la primera y terminas con... bueno, probémosla y veamos.

Tomando una derivada con respecto a\(x\) la Ecuación\(\PageIndex{1}\),\[\frac{\partial^{2} V(x, t)}{\partial x_{2}^{2}} = -\left(\mathbf{L} \frac{\partial^{2} I(x, t)}{\partial t \partial x}\right)\]

Ahora sustituimos por\(\frac{\partial I(x, t)}{\partial x}\) de Ecuación\(\PageIndex{2}\):\[\frac{\partial^{2} V(x, t)}{\partial x_{2}^{2}} = \mathbf{LC} \frac{\partial^{2} V(x, t)}{\partial t_{2}^{2}}\]

Debería ser muy fácil para ti derivar\[\frac{\partial^{2} I(x, t)}{\partial x_{2}^{2}} = \mathbf{LC} \frac{\partial^{2} I(x, t)}{\partial t_{2}^{2}}\]

¡Oh, sé que a todos les encantan las ecuaciones diferenciales! Bueno, echemos un vistazo a estos y solo pensemos por un minuto. Para cualquiera\(V(x, t)\) o\(I(x, t)\), necesitamos encontrar una función que tenga algunos requisitos bastante estrictos. En primer lugar, la función debe ser de la forma tal que no importa si tomamos su segunda derivada en el espacio (\(x\)) o en el tiempo (\(t\)), debe terminar difiriendo en la forma en que se comporta en\(x\) o\(t\) por no más que solo una constante (\(\mathbf{LC}\)).

De hecho, podemos ser más específicos que eso. Primero,\(V(x, t)\) debe tener la misma forma funcional tanto para su como para su\(x\)\(t\) variación. A lo sumo, las dos derivadas deben diferir sólo por una constante. Intentemos una conjetura “afortunada” y dejemos: \[V(x, t) = V_{0} f(x - vt)\]

donde\(V_{0}\) está la amplitud de la tensión, y\(f\) es alguna función de una forma aún indeterminada. Bueno,\[\frac{\partial f(x - vt)}{\partial t} = -(vf')\]

y\[\frac{\partial^{2} f(x-vt)}{\partial t_{2}^{2}} = v^{2} \frac{\text{d} f}{\text{d}}\]

Obsérvese también que\[\frac{\partial^{2} f(x-vt)}{\partial x_{2}^{2}} = f''\]

Ahora, tomemos Ecuaciones\(\PageIndex{6}\)\(\PageIndex{8}\),\(\PageIndex{9}\) y sustituyéndolas en Ecuación\(\PageIndex{4}\):\[V_{0} \frac{\text{d} f}{\text{d}} = \mathbf{LC} V_{0} v^{2} \frac{\text{d} f}{\text{d}}\]

Nuestra suposición “afortunada” funciona como solución siempre y cuando\[v = \pm \frac{1}{\sqrt{\mathbf{LC}}}\]

Entonces, ¿qué es esto\(f(x - vt)\)? Aún no sabemos cuál será su forma funcional real, pero supongamos que en algún momento,\(t_{1}\), la función se parece a Figura\(\PageIndex{1}\).

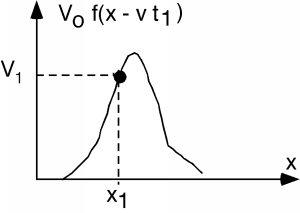
Gráfica de voltaje vs distancia x en el tiempo t_1, cuando la curva de función f alcanza el valor de voltaje de V_1 en el valor del eje x de x_1.

En el punto\(x_{1}\), la función adquiere el valor\(V_{1}\). Ahora, avancemos a tiempo\(t_{2}\). Miramos la función y vemos Figura\(\PageIndex{2}\).

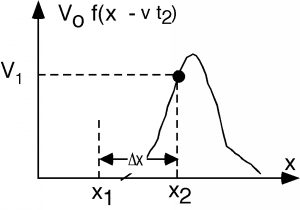
Gráfico de voltaje vs distancia x en tiempo posterior t_2, cuando la curva de la función f se ha movido hacia la derecha y ahora alcanza el valor de voltaje V_1 en el valor x x_2. Hay una distancia de Delta x entre los puntos x_1 y x_2.

Si\(t\) aumenta de\(t_{1}\) a\(t_{2}\), entonces\(x\) tendrá que aumentar de\(x_{1}\) a\(x_{2}\) para que el argumento de\(f\) tenga el mismo valor,\(V_{1}\). Así encontramos\[x_{1} - vt_{1} \equiv x_{2} - vt_{2}\]

que se puede reescribir como\[\frac{x_{2}-x_{1}}{t_{2}-t_{1}} = \frac{\Delta (x)}{\Delta (t)} \equiv v_{p} = \frac{1}{\sqrt{\mathbf{LC}}}\]

donde\(v_{p}\) esta la velocidad con la que la función se mueve a lo largo del eje x! (Utilizamos el subíndice “p” para indicar que lo que tenemos aquí es lo que se llama la velocidad de fase. Nos encontraremos con otra velocidad llamada la velocidad del grupo un poco más tarde en el curso.)

Si hubiéramos “adivinado” una\(f(x + vt)\) para nuestra función, debería ser bastante fácil ver que esto nos hubiera dado una señal moviéndose en la\(x\) dirección menos, en lugar de la\(x\) dirección más. Así denotaremos\[V_{\text{plus}} = V^{+} f \left(x - \frac{1}{\sqrt{\mathbf{LC}}} t\right)\]

la función de voltaje positivo y\[V_{\text{minus}} = V^{-} f\left(x + \frac{1}{\sqrt{\mathbf{LC}}} t\right)\]

la función de voltaje negativo. Observe que ya que estamos tomando la segunda derivada de\(f\) con respecto a\(t\), somos libres de elegir ya sea un argumento\(\frac{1}{\sqrt{\mathbf{LC}}}\) o un\(- \frac{1}{\sqrt{\mathbf{LC}}}\) delante del tiempo dentro\(f\). También tenga en cuenta que estas son nuestras únicas opciones para una solución. Como sabemos por Ecuaciones Diferenciales, una ecuación de segundo orden tiene, como mucho, dos soluciones independientes.

Dado que\(I(x, t)\) tiene la misma ecuación diferencial describiendo su comportamiento, las soluciones para también\(I\) deben ser exactamente de la misma forma. Así podemos dejar\[I_{\text{plus}} = I^{+} f \left(x - \frac{1}{\sqrt{\mathbf{LC}}} t\right)\] representar la función actual que va en la\(x\) dirección positiva, y\[I_{\text{minus}} = I^{-} f \left(x + \frac{1}{\sqrt{\mathbf{LC}}} t\right)\] representar la función de corriente que va negativa.

Ahora, tomemos Ecuación\(\PageIndex{16}\) y Ecuación\(\PageIndex{14}\) y sustituyémoslas en Ecuación\(\PageIndex{1}\):\[\frac{V^{+}}{\sqrt{\mathbf{LC}}} f \left(x - \frac{1}{\sqrt{\mathbf{LC}}} t\right) = \mathbf{L} I^{+} f \left(x - \frac{1}{\sqrt{\mathbf{LC}}} t\right)\]

Esto se puede resolver\(V^{+}\) en términos de\(I^{+}\). \[V^{+} = \sqrt{\frac{\mathbf{L}}{\mathbf{C}}} \ I^{+} \equiv Z_{0} I^{+}\]

donde\(Z_{0} = \sqrt{\frac{\mathbf{L}}{\mathbf{C}}}\) se llama la impedancia característica de la línea de transmisión. Lo dejaremos como un ejercicio al lector para asegurar que efectivamente\(\sqrt{\frac{\mathbf{L}}{\mathbf{C}}}\) tiene unidades de Ohmios. Para practicar y comprender cómo funcionan estas ecuaciones, el lector debe asegurarse de que

\[V^{-} = -\left( \sqrt{\frac{\mathbf{L}}{\mathbf{C}}} I^{-}\right) \equiv -\left(Z_{0} I^{-}\right)\]

¡Observe la diferencia “sutil” aquí, con la presencia de un signo menos frente al RHS de la ecuación!

Hemos pasado por muchas ecuaciones recientemente, así que probablemente valga la pena resumir lo que sabemos hasta ahora.

Las ecuaciones del telégrafo permiten dos soluciones para el voltaje y la corriente en una línea de transmisión. Uno se mueve en la\(x\) dirección y el otro se mueve en la\(-x\) dirección.
Ambas señales se mueven a una velocidad constante\(v_{p}\) dada por la Ecuación\(\PageIndex{21}\).
Las señales de voltaje y corriente están relacionadas entre sí por la impedancia característica\(Z_{0}\), que se encuentra con la ecuación\(\PageIndex{22}\)

\[v_{p} = \frac{1}{\sqrt{\mathbf{LC}}}\]\[Z_{0} = \sqrt{\frac{\mathbf{L}}{\mathbf{C}}}\]\[\frac{V^{+}}{I^{+}} = Z_{0}\]\[\frac{V^{-}}{I^{-}} = -Z_{0}\]