5.6: Líneas Terminadas

Si, por otro lado, tenemos una línea finita, terminada con alguna impedancia de carga, tenemos un problema algo más complicado de tratar (como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Una línea de transmisión finita terminada

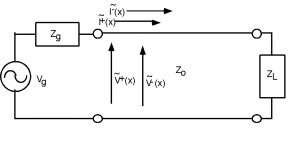
Hay varias cosas que debemos tener en cuenta antes de volver a dirigirnos a la ecuación-tierra. En primer lugar, a diferencia de los problemas transitorios que vimos anteriormente, no puede haber más de dos señales de voltaje y corriente en la línea, solo\(V^{+}\) y\(V^{-}\), (y\(I^{+}\) y\(I^{-}\)). Ya no tenemos el lujo de tener\(V_{1}^{+}\),\(V_{2}^{+}\), etc., porque ahora estamos hablando de un sistema de estado estable. Todas las soluciones transitorias que se acumularon cuando el generador se conectó por primera vez a la línea se han sumado en solo dos ondas.

Así, en la línea tenemos una sola función de voltaje total, que es solo la suma de las ondas de voltaje positivas y negativas\[V(x) = V^{+} e^{- (i \beta x)} + V^{-} e^{i \beta x}\]

y una función de corriente total\[I(x) = I^{+} e^{-(i \beta x)} + I^{-} e^{i \beta x}\]

Tenga en cuenta también que hasta que hayamos resuelto para\(V^{+}\) y\(V^{-}\), no sabemos\(V_{x}\) ni en\(I_{x}\) ningún lugar de la línea. En particular, desconocemos\(V(0)\) y\(I(0)\), lo que nos diría cuál es la impedancia aparente que está buscando dentro de la línea. \[\begin{array}{l} Z_{\text{in}} &=& Z(0) \\   &=& \dfrac{V^{+} + V^{-}}{I^{+} + I^{-}} \end{array}\]

Hasta que sepamos qué tipo de impedancia está viendo el generador, ¡no podemos averiguar cuánto del voltaje del generador se acoplará a la línea! La impedancia de entrada que mira dentro de la línea es ahora una función de la impedancia de carga, la longitud de la línea y la velocidad de fase en la línea. Tenemos que resolver esto antes de que podamos averiguar cómo interactuarán la línea y el generador.

El enfoque que tendremos que tomar es el siguiente. Comenzaremos en el extremo de carga de la línea, y de una manera similar a la que usamos anteriormente, encontraremos una relación entre\(V^{+}\) y\(V^{-}\), dejando su magnitud y fase reales como algo a determinar posteriormente. Entonces podemos propagar los dos voltajes (y corrientes) de nuevo a la entrada, determinar cuál es la impedancia de entrada encontrando la relación de\(\left(V^{+} + V^{-}\right)\) a\(\left(I^{+} + I^{-}\right)\), y a partir de esto, y el conocimiento de las propiedades del generador y su impedancia, determinar cuáles son los voltajes y corrientes reales.

Echemos un vistazo a la carga. Nuevamente utilizamos KVL y KCL (Figura\(\PageIndex{2}\)) para hacer coincidir los voltajes y corrientes en la línea y los voltajes y corrientes en la carga:\[V^{+} e^{-(i \beta L)} + V^{-} e^{i \beta L} = V_{L}\] y\[I^{+} e^{-(i \beta L)} + I^{-} e^{- \beta L} = I_{L}\]

Figura\(\PageIndex{2}\): Haciendo Kirchoff al final de la línea. ¡Cambia las variables!

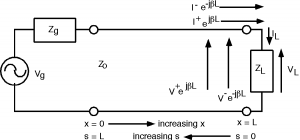
Ahora bien, podríamos sustituir\(\frac{\pm (V)}{Z_{0}}\) las dos corrientes en la línea y\(\frac{V_{L}}{Z_{L}}\) para\(I_{L}\) y luego tratar de resolver\(V_{-}\) en términos de\(V^{+}\) usar Ecuaciones\(\PageIndex{4}\) y\(\PageIndex{5}\), pero podemos ser un poco inteligentes al principio y hacer que nuestro álgebra (complejo) sea un poco bueno limpiador como se muestra en la Figura\(\PageIndex{3}\). Hagamos un cambio de variable y vamos\[s \equiv L - x\]

Figura\(\PageIndex{3}\): ¡\(s=0\)a la carga y así se van los exponenciales!

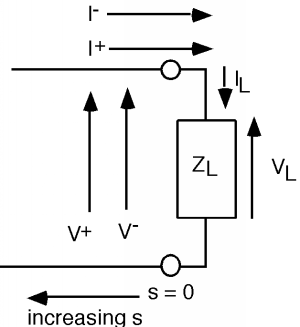
Esto nos da entonces para el voltaje en la línea (usando\(x = L - s\))\[V(s) = V^{+} e^{-(i \beta L)} e^{i \beta L} + V^{-} e^{i \beta L} e^{-i \beta L}\]

Por lo general, simplemente plegamos los\(e^{\pm (i \beta L)}\) términos de fase (constante) con el\(V^{+}\)\(V^{-}\) y y así tenemos:\[V(s) = V^{+} e^{i \beta s} + V^{-} e^{-(i \beta s)}\]

Tenga en cuenta que cuando hacemos esto, ahora tenemos un exponencial positivo en el primer término asociado\(V^{+}\) y un exponencial negativo asociado con el\(V^{-}\) término. Por supuesto, también obtenemos por\(I(s)\): \[I(s) = I^{+} e^{i \beta s} + I^{-} e^{-(i \beta s)}\]

Este cambio ahora mueve nuestro origen al final de carga de la línea, e invierte la dirección del movimiento positivo. Pero, ahora cuando nos conectamos\(e^{i \beta s}\) al valor para\(s\) a la carga\((s = 0)\), las ecuaciones simplifican a:\[V^{+} + V^{-} = V_{L}\] y\[I^{+} + I^{-} = I_{L}\]

que luego reescribimos como\[\frac{V^{+}}{Z_{0}} - \frac{V^{-}}{Z_{0}} = \frac{V_{L}}{Z_{L}}\]

Esto empieza a parecerse casi exactamente a un capítulo anterior. Como recordatorio, resolvemos Ecuación\(\PageIndex{12}\) para\(V_{L}\):\[V_{L} = \frac{Z_{L}}{Z_{0}} \left(V^{+} - V^{-}\right)\]

y sustituirlo\(V_{L}\) en Ecuación\(\PageIndex{10}\):\[V^{+} + V^{-} = \frac{Z_{L}}{Z_{0}} \left(V^{+} - V^{-}\right)\]

De lo que luego resolvemos para el coeficiente de reflexión\(\Gamma_{v}\), la relación de\(V^{-}\) a\(V^{+}\). \[\frac{V^{-}}{V^{+}} \equiv \Gamma_{v} = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}}\]

Tenga en cuenta que dado que, en general,\(Z_{L}\) será complejo, podemos esperar que\(\Gamma_{v}\) también sea un número complejo con tanto una magnitud\(\left| \Gamma_{v} \right|\) como un ángulo de fase\(\theta_{\Gamma}\). También, como en el caso cuando estábamos viendo transitorios,\(\left| \Gamma_{v} \right| < 1\).

Como ahora sabemos\(V^{-}\) en términos de\(V^{+}\), ahora podemos escribir una expresión para\(V(s)\), el voltaje en cualquier lugar de la línea. \[V(s) = V^{+} e^{i \beta s} + V^{-} e^{-(i \beta s)}\]

Obsérvese nuevamente el cambio en los signos en los dos exponenciales. Como nuestra variable espacial\(s\) va en dirección opuesta a\(x\), el\(V^{+}\) fasor ahora va como\(i \beta s\) y el\(V^{-}\) fasor ahora va como\(-(i \beta s)\).

Ahora sustituimos\(V^{-}\) en\(\Gamma_{v} V^{+}\) Ecuación\(\PageIndex{16}\), y por razones que pronto se harán evidentes, factorizar un\(e^{i \beta s}\). \[\begin{array}{l} V(s) &= & V^{+} e^{i \beta s} + \Gamma_{v} V^{+} e^{-(i \beta s)} \\  &= & V^{+} \left(e^{i \beta s} + \Gamma_{v} e^{-(i \beta s)}\right) \\   &= & V^{+} e^{i \beta s} \left(1 + \Gamma_{v} e^{-(2i \beta s)}\right) \end{array}\]

También podríamos haber escrito una ecuación para\(I(s)\), la corriente a lo largo de la línea. Será una buena prueba de su comprensión de las ecuaciones básicas que estamos desarrollando aquí para mostrarse que efectivamente \[I(s) = \frac{V^{+} e^{i \beta s}}{Z_{0}} \left(1 - \Gamma_{v} e^{-(2i \beta s)}\right)\]