2.1: Revisión de Números Complejos y Aritmética
- Page ID
- 84605
Encontraremos muchos usos en la dinámica del sistema para el análisis con números y variables complejos. Es instructivo primero imaginar cómo los números complejos podrían haberse desarrollado históricamente. Parece probable que aparecieron primero en soluciones para raíces de ecuaciones polinómicas. Para ver cómo, examinemos el polinomio de segundo grado, la ecuación cuadrática estándar y sus soluciones. La ecuación cuadrática es
\[a z^{2}+b z+c=0\label{eqn:2.1} \]
donde\(z\) se encuentran las constantes desconocidas y\(a\)\(b\),, y\(c\) son conocidas. La solución estándar para raíces\(z\) es
\[z=-\frac{b}{2 a} \pm \frac{1}{2 a} \sqrt{b^{2}-4 a c}\label{eqn:2.2} \]
Siempre que\(b^{2}-4 a c \geq 0\), la solución vía Ecuación se\(\ref{eqn:2.2}\) pueda calcular fácilmente. Pero supongamos que las constantes tienen valores tales que\(b^{2}-4 a c<0\), de modo que Ecuación\(\ref{eqn:2.2}\) indica la raíz cuadrada de un número negativo. Eso debió parecerle extraño a los matemáticos tempranos. Sin embargo, Ecuación\(\ref{eqn:2.2}\) es la solución correcta independientemente del signo de\(b^{2}-4 a c\), que se puede verificar simplemente sustituyendo Ecuación de\(\ref{eqn:2.2}\) nuevo en Ecuación\(\ref{eqn:2.1}\). Por lo que era necesario reconocer la existencia de la raíz cuadrada de un número negativo e inventar notación y terminología para describir tal número.
Para\(b^{2}-4 a c<0\), podemos escribir
\[\sqrt{b^{2}-4 a c}=\sqrt{(-1)\left(4 a c-b^{2}\right)}=\sqrt{-1} \times \sqrt{4 a c-b^{2}} \equiv j \sqrt{4 a c-b^{2}} \nonumber \]
en el que definimos el número imaginario de la unidad como\(j \equiv \sqrt{-1}\). Quizás los matemáticos tempranos utilizaron el adjetivo “imaginario” porque tal número les parecía irreal. Con esta definición, podemos escribir Ecuación\(\ref{eqn:2.2}\) en la forma
\[z=-\frac{b}{2 a} \pm j \frac{1}{2 a} \sqrt{4 a c-b^{2}} \nonumber \]
A esto se le llama un número complejo, que es la suma de un número normal, o real y un número imaginario (por\(j\) lo que un número real es un número imaginario general).
Si\(x\) y\(y\) son reales, entonces cualquier número complejo se puede escribir en forma rectangular:
Esta forma se llama “rectangular” porque expresa el número complejo en términos de sus componentes rectangulares, o cartesianos,\(x\) y\(y\). \(\ref{eqn:2.3}\)La ecuación es matemáticamente similar a un vector bidimensional v expresado en términos de componentes cartesianos y vectores unitarios\(\mathbf{1}_{\mathbf{x}}\) y\(\mathbf{1}_{\mathbf{y}}\):\(\mathbf{v}=v_{x} \mathbf{1}_{\mathbf{x}}+v_{y} \mathbf{1}_{\mathbf{y}}\). Por lo tanto, podemos representar\(z=x+j y\) gráficamente un número complejo en forma cartesiana similar al utilizado para vectores bidimensionales, como se muestra en la Figura\(\PageIndex{1}\).
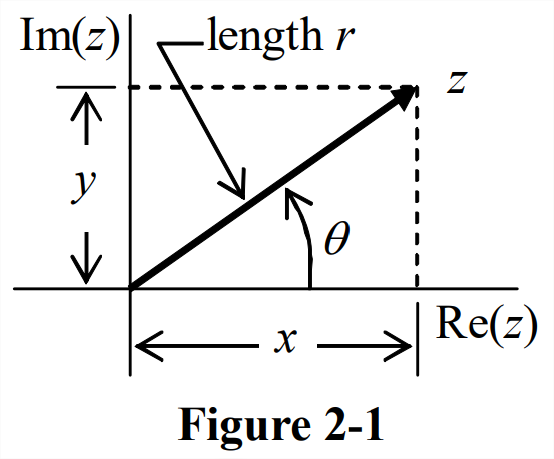
A partir de la Figura\(\PageIndex{1}\), podemos inferir otra manera útil de representar un número complejo. Al definir la magnitud (longitud, valor absoluto, módulo) de\(z\) como el número positivo
\[r=\sqrt{x^{2}+y^{2}}\label{eqn:2.4} \]
podemos escribir
\[z=x+j y=r\left(\frac{x}{r}+j \frac{y}{r}\right)=r(\cos \theta+j \sin \theta)\label{eqn:2.5} \]
En Ecuación\(\ref{eqn:2.5}\), empleamos las funciones trigonométricas estándar de ángulo\(\theta\) originadas en el eje real positivo y definidas positivas en sentido antihorario (CCW), Figura\(\PageIndex{1}\). Ángulo a menudo\(\theta\) se llama el argumento de\(z\). La definición general es
\[\theta=\tan ^{-1}\left(\frac{y}{x}\right)\label{eqn:2.6} \]
Es necesario reconocer la Ecuación\(\ref{eqn:2.6}\) como la tangente inversa de cuatro cuadrantes (o arcotangente). Por ejemplo, si\(y\) es positivo y\(x\) es negativo, entonces la Ecuación\(\ref{eqn:2.6}\) debería dar ángulo\(\theta\) en el segundo cuadrante,\(90^{\circ}<\theta<180^{\circ}\); o, si ambos\(y\) y\(x\) son negativos, entonces la Ecuación\(\ref{eqn:2.6}\) debería dar ángulo\(\theta\) en el cuadrante 3º, \(-180^{\circ}<\theta<-90^{\circ}\)(que también se puede escribir como\(180^{\circ}<\theta<270^{\circ}\)). Desafortunadamente, la función tan −1 o arctan en las calculadoras de mano no calcula la tangente inversa de cuatro cuadrantes, sino que solo considera el signo del cociente\(y/x\), y produce un\(\theta\) valor en el 1er o 4º cuadrantes,\(-90^{\circ}<\theta<+90^{\circ}\). Entonces, si estás evaluando Ecuación\(\ref{eqn:2.6}\) en tu calculadora de mano, necesitas dar cuenta de los signos tanto de y como de x, y necesitas modificar apropiadamente la respuesta dada por tu calculadora. Si está evaluando Ecuación\(\ref{eqn:2.6}\) en MATLAB, entonces debe usar la función tangente inversa de cuatro cuadrantes de MATLAB, atan2 (y, x).
La ecuación\(\ref{eqn:2.5}\) es solo un resultado intermedio. Para lograr la forma final deseada, reescribimos la ecuación\(\ref{eqn:2.5}\) usando las conocidas expansiones de la serie Taylor power para funciones sinusoidales, cosenales y exponenciales:
\[z=r(\cos \theta+j \sin \theta)=r\left[\left(1-\frac{\theta^{2}}{2 !}+\frac{\theta^{4}}{4 !}-\ldots\right)+j\left(\theta-\frac{\theta^{3}}{3 !}+\frac{\theta^{5}}{5 !}-\ldots\right)\right] \nonumber \]
\[z=r(\cos \theta+j \sin \theta)=r\left(1+(j \theta)+\frac{(j \theta)^{2}}{2 !}+\frac{(j \theta)^{3}}{3 !}+\frac{(j \theta)^{4}}{4 !}+\frac{(j \theta)^{5}}{5 !}+\ldots\right) \equiv r e^{j \theta} \nonumber \]
\[z=r e^{j \theta}\label{eqn:2.7} \]
El resultado importante
\[\cos \theta+j \sin \theta=e^{j \theta}\label{eqn:2.8} \]
se conoce como la ecuación de Euler (después de Leonhard Euler, 1707-1783, matemático y físico suizo). Ver tarea Problema 2.1 para otras ecuaciones estrechamente relacionadas con la Ecuación\(\ref{eqn:2.8}\).
Un número complejo en la forma\(z=r e^{j \theta}\) se llama la forma polar porque emplea coordenadas polares\(r\) y\(\theta\). Podemos visualizar el término exponencial complejo en\(e^{j \theta}\) sí mismo como una manecilla de reloj en el plano complejo, Figura\(\PageIndex{1}\); la manecilla del reloj tiene longitud unitaria, y se gira CCW por ángulo\(\theta\) desde la posición de las 3 en punto. De igual manera, el número complejo completo\(z=r e^{j \theta}\) representa una manecilla de reloj de longitud\(r\) que se gira CCW por ángulo\(\theta\) desde la posición de las 3 en punto, por lo que a menudo\(z=r \angle \theta\) se usa la notación, donde el símbolo\(\angle\) significa “ángulo”.
Ocasionalmente necesitaremos convertir un número complejo de forma rectangular a forma polar usando Ecuaciones\(\ref{eqn:2.4}\) y\(\ref{eqn:2.6}\). Las funciones abs y angle de MATLAB son especialmente útiles para esta tarea, como se ilustra en el Ejemplo 2 Aritmético Complejo-siguiente.
También necesitaremos usar aritmética compleja, así que vamos a revisar (de tus cursos de matemáticas) algunos de los conceptos básicos, suponiendo que tenemos dos números complejos\(z\) y\(w\) expresados tanto en forma rectangular como polar:
\(z=x+j y=r e^{j \theta}\)y\(w=u+j v=q e^{j \phi}\), donde\(x\),\(y\),\(r\),\(\theta\),,\(u\),\(v\),\(q\), y\(\phi\) todos son reales.
Suma o resta, rectangular:\(z \pm w=(x \pm u)+j(y \pm v)\).
Suma o resta, polar:\(r e^{j \theta} \pm q e^{j \phi} \equiv Z \equiv R e^{j \Theta}\).
\[Z=r \cos \theta+q \cos \phi \pm j(r \sin \theta+q \sin \phi) \nonumber \]
\[R=\sqrt{[\operatorname{Re}(Z)]^{2}+[\operatorname{Im}(Z)]^{2}}=\sqrt{r^{2}+q^{2}+2 r q \cos (\theta-\phi)} \nonumber \]
\[\Theta=\tan ^{-1}[\operatorname{Im}(Z) / \operatorname{Re}(Z)]=\tan ^{-1}[\pm(r \sin \theta+q \sin \phi) /(r \cos \theta+q \cos \phi)] \nonumber \]
Multiplicación, rectangular:\(z \times w=x u+j(x v+y u)+j^{2}(y v)=(x u-y v)+j(x v+y u)\).
Multiplicación, polar:\(z \times w=r q e^{j(\theta+\phi)}\).
El conjugado complejo de se define como\(z=x+j y=r e^{j \theta}\) se define como\(\bar{z}=x-j y=r e^{-j \theta}\), de manera que el producto de un número complejo y su conjugado es real, e igual al cuadrado de la magnitud:\(z \bar{z}=x^{2}+j(-x y+y x)-j^{2} y^{2}=x^{2}+y^{2}=r^{2}\), o más fácilmente en forma polar,\(z \bar{z}=r e^{j \theta} \times r e^{-j \theta}=r^{2} e^{j(\theta-\theta)}=r^{2}\). Supongamos que tenemos el cociente de dos números complejos\(z\) por\(w\), ambos en forma rectangular, y deseamos echar el resultado en forma rectangular estándar; es práctica común primero multiplicar tanto el denominador como el numerador por el conjugado del denominador, formando así un denominador real:
División, rectangular:\(\frac{z}{w}=\frac{x+j y}{u+j v}=\frac{(x+j y)(u-j v)}{(u+j v)(u-j v)}=\frac{x u+y v}{u^{2}+v^{2}}+j \frac{-x v+y u}{u^{2}+v^{2}}\)
División, polar,\(\frac{z}{w}=\frac{r}{q} e^{j(\theta-\phi)}\)
Colocar la siguiente fracción compleja en forma rectangular estándar, luego convertirla en forma polar:\[z=\frac{3-j 4}{1+j 2}=\frac{(3-j 4)(1-j 2)}{(1+j 2)(1-j 2)}=\frac{3-8+j(-6-4)}{5}=-1-j 2 \nonumber \]
Solución
\[r=\sqrt{(-1)^{2}+(-2)^{2}}=2.236 \nonumber \]
\[\theta=\tan ^{-1}\left(\frac{-2}{-1}\right)=-116.6^{\circ} \times \frac{\pi \mathrm{rad}}{180^{\circ}}=-2.034 \mathrm{rad} \nonumber \]
\[\Rightarrow \quad z=\frac{3-j 4}{1+j 2}=-1-j 2=2.236 e^{j\left(-116.6^{\circ}\right)} \equiv 2.236 \angle(-2.034 \mathrm{rad}) \nonumber \]
Tenga\(\tan^{-1}(2)\) en cuenta que cuando toma su calculadora de mano, da 63.43°. Debido a que realmente estás tratando de encontrar\(\tan^{-1}(-2/-1)\), debes reconocer que el ángulo correcto está en el cuadrante 3 y, por lo tanto, sumar +180° o —180° a la solución de la calculadora para obtener el resultado correcto, +243.4° o —116.6°.
Colocar la siguiente fracción compleja en forma rectangular estándar, luego convertirla en forma polar:\[z=\frac{(3-j 2)(4+j)}{2-j 3}-7+j 4=\frac{(14-j 5)(2+j 3)}{(2-j 3)(2+j 3)}-7+j 4=\frac{43+j 32}{13}-7+j 4 \nonumber \]
Solución
\[z=\left(\frac{43}{13}-7\right)+j\left(\frac{32}{13}+4\right)=-3.692+j 6.462 \nonumber \]
\[r=\sqrt{(-3.692)^{2}+(6.462)^{2}}=7.442 \nonumber \]
\[\theta=\tan ^{-1}\left(\frac{6.462}{-3.692}\right)=-60.255^{\circ}+180^{\circ}=119.7^{\circ} \nonumber \]
\[\Rightarrow \quad z=\frac{(3-j 2)(4+j)}{2-j 3}-7+j 4=-3.692+j 6.462=7.442 e^{j 119.7^{\circ}} \nonumber \]
A continuación se presenta una solución del Ejemplo 2 Aritmético Complexo en términos de operaciones de MATLAB:
>> z =( 3-2j) * (4+j)/(2-3j) -7+4j
z = -3.6923 + 6.4615i
>> r=abs (z), theta=ángulo (z)
r = 7.4421
theta = 2.0899
>> thetadeg=theta*180/pi
thetadeg = 119.7449
Tenga en cuenta que MATLAB prefiere, y da resultados en términos de la unidad número imaginario denotado como\(i\), pero reconoce nuestra notación de\(j\). Tenga en cuenta también que el radián es la unidad predeterminada de MATLAB para ángulos: si desea un resultado de ángulo MATLAB en grados, debe convertir de radianes; también, si desea calcular una función trigonométrica de un ángulo, debe expresar ese ángulo en radianes.


