4.4: Periodo, Frecuencia y Fase de las Señales Periódicas

Consideremos de manera más general las cantidades temporales de señales periódicas, representadas en nuestras aplicaciones por sinusoides. Periodo normalmente\(T_p\) se mide en segundos por ciclo, por lo que la frecuencia cíclica\(f\) en ciclos por segundo es la inversa de periodo,\(f=1 / T_{p}\). Además, el periodo está relacionado con la frecuencia circular\(\omega\) por\(\omega T_{p}=2 \pi\) radianes, de manera que

\[\text { circular frequency } \omega=\frac{2 \pi}{T_{p}} \equiv 2 \pi f \frac{\mathrm{rad}}{\mathrm{sec}}, \text { and cyclicfrequency } f=\frac{\omega}{2 \pi} \mathrm{Hz}\left(\frac{\text { cycles }}{\mathrm{sec}}\right)\label{eqn:4.16} \]

Estas relaciones entre período y frecuencia merecen ser entendidas completamente e incluso memorizadas, ya que las usamos mucho en la dinámica del sistema.

También es importante entender cómo se manifiesta la fase FRF en las gráficas de historia de tiempo de entrada y salida. Esta discusión es general, aplicable a cualquier sistema LTI. Supongamos que hay trazados en la misma gráfica los historiales de tiempo sinusoidales de estado estacionario tanto de la entrada\(u(t)\) como de la salida\(x(t)\), como en la Figura\(\PageIndex{1}\) de la página siguiente. Queremos calcular la fase FRF a partir de mediciones en las parcelas de historia de tiempo. Primero, encuentra la\(x(t)\) cresta positiva más cercana a la izquierda de una\(u(t)\) cresta positiva de referencia, como se muestra en la Figura\(\PageIndex{1}\). Mida el intervalo de tiempo positivo\(T_{l e a d}\) en segundos que\(x(t)\) lleva\(u(t)\). (Tenga en cuenta que\(T_{l e a d}\) también puede medir comparando bajadas o ceros positivos o negativos, como se muestra en la Figura)\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Medición de fase de respuesta de frecuencia a partir de gráficos de historia

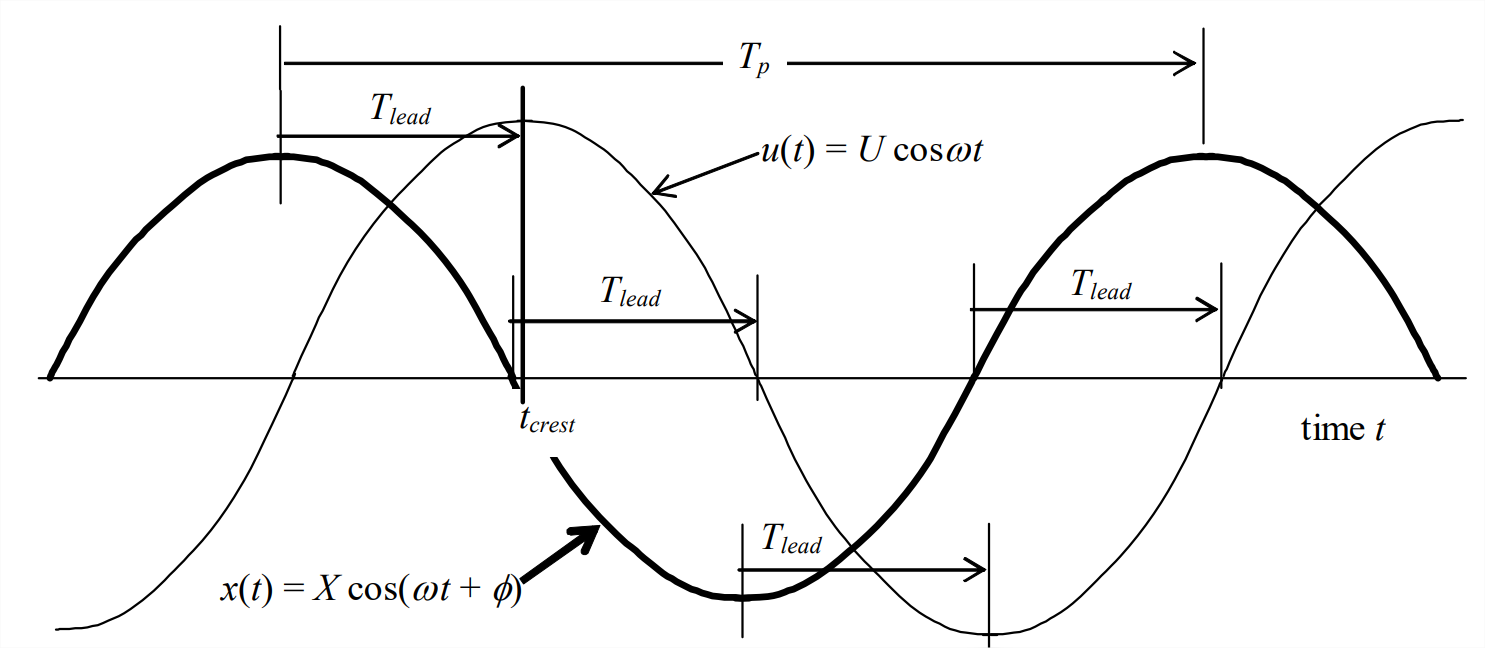
Ahora, refiriéndose a las crestas positivas, denotemos como\(t_{\text {crest}}\) el instante correspondiente a una cresta positiva de entrada\(u(t)\). Entonces vemos por el dibujo que

\[\cos \omega t_{c r e s t}=+1 \quad \Rightarrow \quad \omega t_{c r e s t}=2 \pi n, \text { where } n \text { is some integer } \nonumber \]

\[\cos \left(\omega\left[t_{\text {crest}}-T_{\text {lead}}\right]+\phi\right)=+1 \quad \Rightarrow \quad \omega\left[t_{\text {crest}}-T_{\text {lead}}\right]+\phi=2 \pi n \nonumber \]

La comparación de estas dos ecuaciones muestra que\(\omega\left[-T_{l e a d}\right]+\phi=0\), lo que da la ecuación básica para el ángulo de fase (definido positivo como un lead, negativo como un lag):

\[\phi=\omega T_{\text {lead}}=\frac{2 \pi}{T_{p}} T_{\text {lead}}=2 \pi \frac{T_{\text {lead}}}{T_{p}} \operatorname{rad} \times \frac{360 \mathrm{deg}}{2 \pi \mathrm{rad}}=360 \times \frac{T_{\text {lead}}}{T_{p}} \mathrm{deg}\label{eqn:4.17a} \]

donde\(T_{p}(=2 \pi / \omega=1 / f)\) es el periodo de la entrada y la salida en estado estacionario, como se muestra en la Figura\(\PageIndex{1}\).

Si elige seleccionar la\(x(t)\) cresta positiva más cercana a la derecha de una\(u(t)\) cresta de referencia, entonces está encontrando un retraso de tiempo\(T_{l a g}\), que es una ventaja negativa. En este caso, se puede encontrar el ángulo de fase, con el signo correcto, desde

\[\phi=-\omega T_{l a g}=-360 \times \frac{T_{l a g}}{T_{p}} \operatorname{deg}\label{eqn:4.17b} \]

Ecuaciones\(\ref{eqn:4.17a}\) y\(\ref{eqn:4.17b}\) dan\(\phi\) en el rango 0°\(\leq\)\(\phi\) < 360°, lo cual es correcto pero no común. No es común porque el arcoangente de cuatro cuadrantes se expresa convencionalmente (en MATLAB, por ejemplo) en el rango −180°\(\leq\)\(\phi\) < +180°. Por lo tanto, si se mide y calcula por el procedimiento por encima de una fase\(\phi\)\(\geq\) +180°, entonces es convencional sustituirlo por (\(\phi\)− 360°).\(\phi\) Por ejemplo, si tuvieras que medir y calcular la fase\(\phi\) = 262°, entonces sería convencional expresarla como un retraso de fase, φ = (262° − 360°) = −98°, en lugar de una ventaja de fase de 262°.