15.4: Ejemplo de Control PD

A continuación, consideramos el efecto del control derivado, el tercer tipo de operación sobre la señal de error indicada en las Ecuaciones 15.1.1 y 15.1.2. El término derivado (con\(b_{d}=1\)) en la señal del actuador\(w(t)\) es\(P \tau_{d} \times d e_{e} / d t\). Este término es proporcional a la tasa de cambio de la señal de error, por lo que anticipa, en cierto sentido, cualquier incremento en el error, y actúa para oponerse a ese incremento. La acción derivada se utiliza en combinación con acción proporcional o acción proporcional-integral, pero no por sí misma. Mientras que la acción proporcional tiene el efecto de un resorte lineal restaurador, la acción derivada tiene el efecto de un amortiguador viscoso. Por lo tanto, el control derivado por sí mismo fallaría en proporcionar una acción que fuerce la salida del sistema hacia el valor deseado.

Un chequeo de la realidad es apropiado en este punto. La salida derivada\(x_{d}(t) \equiv \dot{e}_{e}\) de un controlador PID ideal en la Ecuación 15.1.1 es físicamente poco realista, ya que no es posible medir exactamente, en tiempo real, la derivada\(\dot{e}_{e}\) de la señal de error. La medición exacta en tiempo real de una derivada en un instante requeriría información sobre los valores e e y futuros de la señal, pero se desconocen los valores futuros. Otra manifestación del irrealismo del término derivado es la función de transferencia asociada\(X_{d} / E_{e}=s / 1\), que se escribe aquí como una fracción en el lado derecho para enfatizar que el orden polinomio (in\(s\)) del numerador es mayor que el del denominador. Así, esta función de transferencia es acausal, lo que significa que la salida de corriente del diferenciador ideal debe depender de los valores futuros, así como pasados y presentes, de la señal de error (ver Bélanger, 1995, p. 440).

^{Dado que el diferenciador exacto de la Ecuación 15.1.1 no se puede realizar físicamente, un controlador PD real a menudo incluye un diferenciador aproximado en forma de un filtro de paso alto de primer orden descrito por la ODE\(\varepsilon \tau_{d} \dot{x}_{d}+x_{d}=\dot{e}_{e}\); en esta ODE,\(\tau_{d}\) es la derivada} constante de tiempo, y\(\mathcal{E}\) es un pequeño número positivo típicamente seleccionado para estar en el rango de 0.1 a 0.3 (Ogata, 2001, páginas 700 y 727). La función de transferencia de este diferenciador aproximado es\(X_{d}(s) / E_{e}(s)=s /\left(\varepsilon \tau_{d} s+1\right)\), que es causal, por lo tanto físicamente realizable. Para las señales de error que varían lentamente en el tiempo en relación con la frecuencia de ruptura del filtro de paso alto\(1 /\left(\varepsilon \tau_{d}\right)\) rad/s, este diferenciador aproximado es muy preciso, pero para señales de error más rápidas la salida del dispositivo no logra aproximarse a la derivada de la señal de error (ver tarea Problema 15.4). En la práctica, por lo tanto, la selección de parámetros\(\tau_{d}\) y\(\mathcal{E}\) se basa al menos parcialmente en la velocidad de las señales que se espera que procese el controlador PD. El funcionamiento de un controlador PD real usando el diferenciador aproximado es\(w(t)=P\left[e_{e}(t)+\tau_{d} x_{d}(t)\right]\); puede mostrar fácilmente que la función de transferencia del controlador PD real es

\[\frac{W(s)}{E_{e}(s)}=P\left(1+\tau_{d} \frac{X_{d}(s)}{E_{e}(s)}\right)=P\left(1+\frac{\tau_{d} s}{\varepsilon \tau_{d} s+1}\right)=P\left(\frac{(1+\varepsilon) \tau_{d} s+1}{\varepsilon \tau_{d} s+1}\right). \nonumber \]

Es estándar en las discusiones introductorias describir el control de la EP en el contexto del diferenciador ideal (aunque físicamente irrealizable)\(x_{d} \equiv \dot{e}_{e}\), en lugar del diferenciador aproximado más realista\(\mathcal{E} \tau_{d} \dot{x}_{d}+x_{d}=\dot{e}_{e}\). El diferenciador aproximado conduce a un sistema de orden superior y álgebra mucho más complicada, a partir del cual es difícil inferir características físicas básicas del control de PD. Por lo tanto, en el resto de esta sección, y en el examen continuado de este mismo ejemplo en la tarea Problema 15.1 y en la Sección 16.2, seguiremos el procedimiento introductorio estándar y utilizaremos la función de transferencia de controlador PD ideal\(P\left(1+\tau_{d} s\right)\) de la Ecuación 15.1.2. La mayoría de los resultados teóricos producidos por este enfoque son buenas aproximaciones a lo que se realizaría a partir de un controlador PD real correctamente diseñado, al menos para entradas y salidas que varían suficientemente lentamente.

Figura\(\PageIndex{1}\): Control proporcional de la posición del rotor. (Copyright; autor vía fuente)

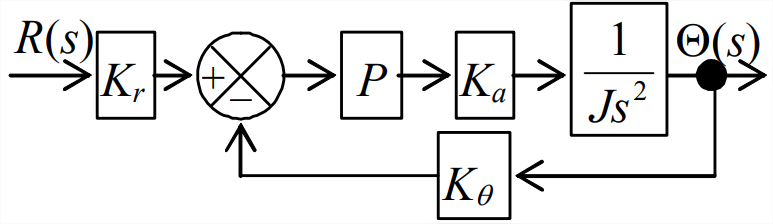
Para ilustrar el control proporcional-derivado (PD), consideramos nuevamente el problema de controlar la posición\(\theta(t)\) de un rotor con inercia significativa\(J\), como se discute en el Capítulo 14 [Figuras 14.1.1, 14.2.1, y 14.3.1, y Ecuaciones 14.1.1 y 14.1.2]. Recordemos que la entrada al sistema es la configuración del operador\(r(t)\). Dejemos de lado los momentos de perturbación,\(M_{d}(t)=0\). La figura\(\PageIndex{1}\) es el diagrama de bloques de Laplace para el sistema controlado por P, del cual son\(G(s)=P K_{a} /\left(J s^{2}\right)\) y las funciones de transferencia de bucle\(H(s)=K_{\theta}\). Por lo tanto, usamos la Ecuación 14.4.6 para encontrar

\[C L T F(s)=\frac{\Theta(s)}{R(s)}=K_{r} \times \frac{N_{G} D_{H}}{D_{G} D_{H}+N_{G} N_{H}}=K_{r} \times \frac{P K_{a}}{J s^{2}+P K_{a} K_{\theta}} \equiv \frac{K_{r}}{K_{\theta}} \frac{\omega_{n}^{2}}{s^{2}+\omega_{n}^{2}} \nonumber \]

La frecuencia natural no amortiguada en esto\(\operatorname{CLTF}(s)\) se define por\(\omega_{n}^{2}=P K_{a} K_{\theta} / J\). Supongamos que la entrada es una función de paso con magnitud\(R_{H}: r(t)=R_{H} H(t)\). Para esta entrada, la transformación de Laplace de respuesta es\(\Theta(s)=\frac{R_{H}}{s} \frac{K_{r}}{K_{\theta}} \frac{\omega_{n}^{2}}{s^{2}+\omega_{n}^{2}}\). Aplicación de la transformada inversa La ecuación 15.2.23, con\(\zeta=0\), da la respuesta escalonada\(\theta(t)=\left(R_{H} K_{r} / K_{\theta}\right)\left(1-\cos \omega_{n} t\right)\). Se trata de un movimiento no amortiguado que oscila para siempre alrededor del valor final deseado,\(\theta=R_{H} K_{r} / K_{\theta}\) [ver Ecuación 7.3.8 y Figura 7.3.2], por lo que es inaceptable para un sistema de control de posición. En este caso, el control P por sí solo tiene el efecto de un resorte lineal restaurador, pero no proporciona amortiguación.

Figura\(\PageIndex{2}\): Control ideal proporcional-derivado (PD) de la posición del rotor. (Copyright; autor vía fuente)

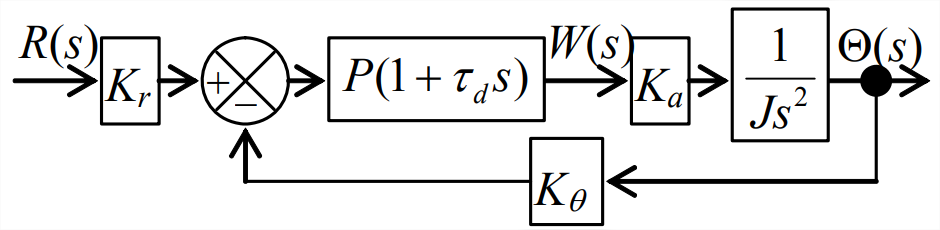
Para mejorar el desempeño del control, agregamos acción derivada, actualizando del control P al control PD ideal. A partir de la Ecuación 15.1.2 con\(b_{i}=0\) y\(b_{d}=1\), la función de transferencia del controlador PD ideal es\(P\left(1+\tau_{d} s\right)\), por lo que el diagrama de bloques de Laplace para el sistema de bucle cerrado se convierte en el que se muestra en la\(\PageIndex{2}\) Figura En este caso, la función de transferencia de rama directa de bucle es\(G(s)=P\left(1+\tau_{d} s\right) K_{a} /\left(J s^{2}\right)\), por lo que la función de transferencia de bucle cerrado del sistema es

\[\frac{\Theta(s)}{R(s)}=K_{r} \times \frac{N_{G} D_{H}}{D_{G} D_{H}+N_{G} N_{H}}=K_{r} \times \frac{P\left(1+\tau_{d} s\right) K_{a}}{J s^{2}+P\left(1+\tau_{d} s\right) K_{a} K_{\theta}}=\frac{K_{r} P K_{a}\left(1+\tau_{d} s\right)}{J s^{2}+P K_{a} K_{\theta} \tau_{d} s+P K_{a} K_{\theta}} \nonumber \]

Como hicimos en las Ecuaciones 15.2.19 y 15.2.20, que se aplican al control PI (pero de una planta diferente), ahora podemos reescribir esta función de transferencia de circuito cerrado PD en términos de parámetros apropiados para un sistema de ^segundo orden amortiguado:

\[\frac{\Theta(s)}{R(s)}=\frac{K_{r}}{K_{\theta}} \frac{\left(P K_{a} K_{\theta} / J\right)\left(\tau_{d} s+1\right)}{s^{2}+\left(P K_{a} K_{\theta} / J\right) \tau_{d} s+\left(P K_{a} K_{\theta} / J\right)} \equiv \frac{K_{r}}{K_{\theta}} \frac{\omega_{n}^{2}\left(\tau_{d} s+1\right)}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}\label{eqn:15.27} \]

En\(\ref{eqn:15.27}\) la Ecuación, la frecuencia natural no amortiguada y la relación de amortiguación viscosa son, respectivamente:

\[\omega_{n}=\sqrt{\frac{P K_{a} K_{\theta}}{J}} \text { and } \zeta=\frac{1}{2 \omega_{n}} \frac{P K_{a} K_{\theta}}{J} \tau_{d}=\frac{1}{2} \omega_{n} \tau_{d}\label{eqn:15.28} \]

El efecto obvio de la acción derivada es agregar amortiguación al sistema de ^segundo orden, y esta amortiguación mejora el rendimiento del control (ver tarea Problema 15.1). Obsérvese también que el término\(\omega_{n}^{2} \tau_{d} S\) en el numerador de Ecuación\(\ref{eqn:15.27}\) hace que este sistema no sea estándar en relación con la ecuación de definición 9.2.2 de la ODE estándar de ^segundo orden. El carácter no estándar significa, entre otras cosas, que las especificaciones de respuesta escalonada derivadas en la Sección 9.8 no se aplican exactamente para este sistema.