16.3: Criterios de estabilidad de Routh

Denotamos la función de transferencia de un sistema LTI de orden\(n\) ^th como\(T F(s)=\frac{\operatorname{Num}(s)}{\operatorname{Den}(s)}\), en el que\(\operatorname{Den}(s)\) es un polinomio de\(n\) ^th grado en\(s\). Como se deriva en la Sección 16.1, el sistema es estable o inestable dependiendo de los signos de las raíces de la ecuación característica,

\[\operatorname{Den}(p)=a_{1} p^{n}+a_{2} p^{n-1}+\cdots+a_{n} p+a_{n+1}=0\label{eqn:16.33} \]

Para una estabilidad positiva, debemos tener\(\operatorname{Re}\left(p_{k}\right)<0\) para todas las raíces,\(k=1,2, \ldots, n\). Las raíces dependen de los coeficientes polinomiales\(a_{1}, a_{2}, \ldots, a_{n}, a_{n+1}\), por lo que parecería que el estado de estabilidad podría determinarse directamente a partir de estos coeficientes, sin necesidad de calcular las raíces. Este es efectivamente el caso, y las condiciones que estos coeficientes deben satisfacer para una estabilidad positiva se conocen como criterios de estabilidad de Routh (después de Edward John Routh, 1831-1907, matemático, físico y educador inglés, quien desarrolló el marco sistemático). Estos criterios cuantitativos pueden escribirse para un sistema de cualquier orden\(n\), pero se vuelven progresivamente más complicados a medida que\(n\) aumenta. ^{Por esa razón, examinamos en esta sección solo los criterios para los sistemas de primer orden, segundo y tercero; los criterios de Routh para los sistemas de 4 º orden se presentan en la tarea Problema 16.9 (c).}

El primer requisito para que un sistema de cualquier orden, para que el sistema sea estable positivamente, es que todos los coeficientes de Ecuación característica\(\ref{eqn:16.33}\) sean distintos de cero y tengan el mismo signo. Esta es una condición necesaria pero, para\(n > 2\), no una condición suficiente para la estabilidad. Considere el caso más simple, cualquier sistema ^de primer orden:

\[\operatorname{Den}(p)=a_{1} p+a_{2}=0 \Rightarrow p=-\frac{a_{2}}{a_{1}}\label{eqn:16.34} \]

Es claro que\(p<0\) si\(a_{1}\) y\(a_{2}\) son ambos distintos de cero y de la misma polaridad, por lo que no se requiere otra condición para la estabilidad. Considere a continuación cualquier sistema de orden 2 ^nd:

\[\operatorname{Den}(p)=a_{1} p^{2}+a_{2} p+a_{3}=0\label{eqn:16.35} \]

La fórmula cuadrática da las siguientes raíces de Ecuación\(\ref{eqn:16.35}\):

\[p_{1,2}=-\frac{a_{2}}{2 a_{1}} \pm \sqrt{\left(\frac{a_{2}}{2 a_{1}}\right)^{2}-\frac{a_{3}}{a_{1}}}\label{eqn:16.36} \]

Un estudio cuidadoso de la Ecuación\(\ref{eqn:16.36}\) muestra que estas raíces tienen partes reales negativas solo si\(a_{1}\),\(a_{2}\) y\(a_{3}\) todas son distintas de cero y tienen el mismo signo. Por lo tanto, para ^{el sistema de segundo} orden, el requisito de que los tres coeficientes polinomiales sean distintos de cero y tengan el mismo signo es una condición suficiente y necesaria para la estabilidad. Tenga en cuenta que\(a_{2} = 0\) significa que el sistema tiene amortiguación cero; si, además,\(a_{1}\) y\(a_{3}\) tienen el mismo signo, entonces la respuesta de vibración libre del sistema es pura oscilación sinusoidal (a la frecuencia natural) con amplitud constante. En este caso, el sistema no es inestable, ya que la respuesta está acotada, pero tampoco es exponencialmente estable; la respuesta no decae a un estado de equilibrio estático.

Finalmente, consideremos el sistema de ^tercer orden más desafiante:

\[\operatorname{Den}(p)=a_{1} p^{3}+a_{2} p^{2}+a_{3} p+a_{4}=0\label{eqn:16.37} \]

Para que el sistema sea estable,\(a_{1}\),\(a_{2}\),\(a_{3}\) y\(a_{4}\) todos deben ser distintos de cero y tener el mismo signo. El otro requisito de estabilidad positiva de un sistema ^{de tercer} orden establece límites superiores e inferiores en el producto\(a_{1} \times a_{4}\):

\[a_{2} \times a_{3}>a_{1} \times a_{4}>0\label{eqn:16.38} \]

La derivación de estos dos criterios de Routh para la estabilidad de un sistema ^{de tercer} orden es relativamente simple, pero más larga de lo necesario para nuestro estudio; se presenta claramente por Cannon, 1967, páginas 406-409.

Evaluemos los criterios de estabilidad de Routh aplicados al sistema de ^tercer orden representado en la Figura\(\PageIndex{1}\). Es similar al sistema de la Sección 14.3 para el control de salida-posición-retroalimentación de la posición del rotor, pero hay dos adiciones a ese sistema. En primer lugar, existe la fricción del rodamiento que produce un momento rotacional pasivo\(-c_{\theta} \dot{\theta}\),\(c_{\theta}\) siendo la constante de amortiguación viscosa. ^{En segundo lugar, hay, en la rama de retroalimentación aguas abajo del sensor de posición, un filtro eléctrico de paso bajo de primer orden con constante de tiempo\(\tau_{L}\).} El filtrado de las señales de voltaje del sensor de esta manera es muy común en la práctica. El propósito habitual del filtrado paso bajo es cortar los componentes eléctricos de alta frecuencia de la señal del sensor. Tales componentes no deseados pueden surgir de la electrónica en un sensor “ruidoso”, de campos electromagnéticos desviados y/o cables eléctricos mal blindados, e incluso de vibraciones mecánicas extrañas. Por lo que la función de reducción de amplitud de un filtro de paso bajo es casi siempre beneficiosa para el funcionamiento del sistema de control. Sin embargo, un filtro de paso bajo también cambia la fase de las señales del sensor, además de reducir la amplitud del ruido de alta frecuencia, como se muestra en la Figura 4.3.2.

^{Figura\(\PageIndex{1}\): Diagrama funcional de un sistema de control de posición-retroalimentación del rotor con un filtro paso bajo de primer orden en la rama de retroalimentación.} (Copyright; autor vía fuente)

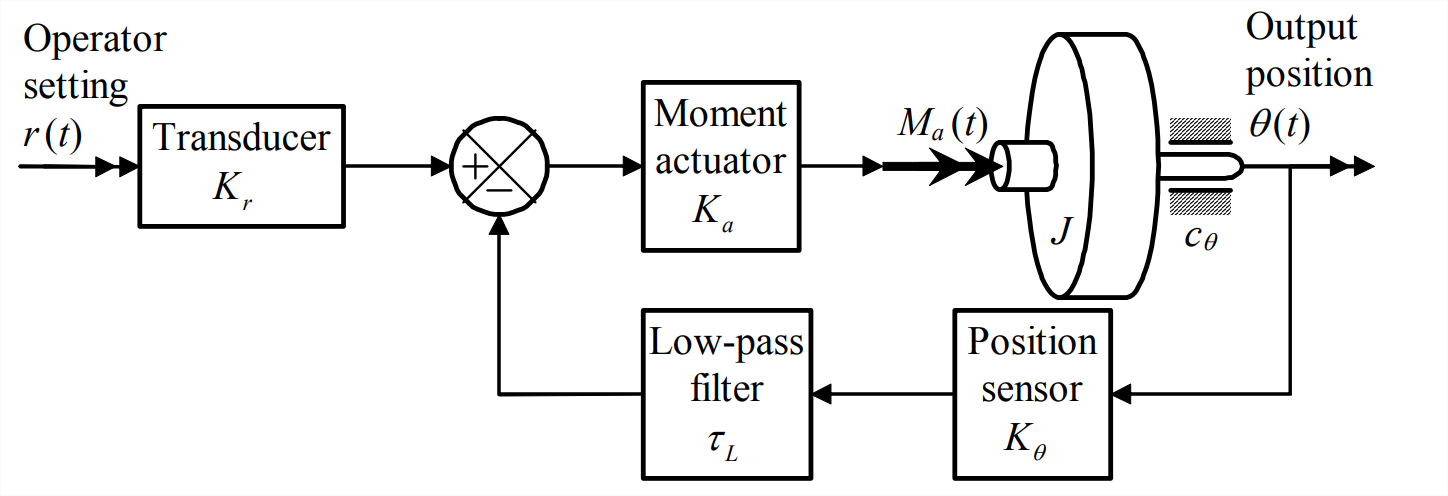
Los cambios de fase pueden producir efectos adversos en los sistemas de control, incluyendo la reducción de la efectividad del control y la degradación de la estabilidad del sistema, incluso a inestabilidad. ^{De la Figura 4.3.2, vemos que el desplazamiento de fase extremo introducido por un filtro paso bajo de primer orden es −90°, y podemos pensar en esto como “casi cambiando el signo” de la señal que pasa por el filtro.} Según los criterios de Routh, el cambio de un signo puede producir inestabilidad. ^{(El efecto sobre la estabilidad sería aún más dramático si hubiera un filtro de paso bajo de segundo orden, en lugar de 1 orden, en la rama de retroalimentación, Figura 10.2.1 con\(\zeta>\sim 0.5\); el desplazamiento de fase extremo producido por un filtro de segundo orden es −180°, que es un} cambio completo de señal en la señal que pasa por el filtro. Ver tarea Problema 16.5.)

La ODE de movimiento para el rotor amortiguado proviene de la Ecuación 3.3.2:\(J \dot{p}+c_{\theta} p= J \ddot{\theta}+c_{\theta} \dot{\theta}=M_{a}(t)\). Con la notación\(L[\theta(t)] \equiv \Theta(s)\), la transformada de Laplace para cero ICs de la ODE de movimiento es\(\left(J s^{2}+c_{\theta} s\right) \Theta(s)=L\left[M_{a}(t)\right]\), de manera que la función de transferencia de la planta básica de rotor amortiguado es

\[\frac{\Theta(s)}{L\left[M_{a}(t)\right]}=\frac{1}{J s^{2}+c_{\theta} s}\label{eqn:16.39} \]

Con la función de transferencia de planta Ecuación\(\ref{eqn:16.39}\) y función de transferencia de filtro de paso bajo Ecuación 13.1.3, la Figura\(\PageIndex{2}\) es el diagrama de bloques de Laplace para el sistema de la Figura\(\PageIndex{1}\). Las funciones de transferencia de ramificación para el bucle en la Figura\(\PageIndex{1}\) son\(G(s)=\frac{K_{a}}{J s^{2}+c_{\theta} s}\) y\(H(s)=\frac{K_{\theta}}{\tau_{L} s+1}\). Por lo tanto, con el uso de la Ecuación 14.4.6, encontramos la siguiente función de transferencia de bucle cerrado:

\[\frac{\Theta(s)}{R(s)}=K_{r} \times \frac{N_{G} D_{H}}{D_{G} D_{H}+N_{G} N_{H}}=K_{r} \times \frac{K_{a}\left(\tau_{L} s+1\right)}{\left(J s^{2}+c_{\theta} s\right)\left(\tau_{L} s+1\right)+K_{a} K_{\theta}} \nonumber \]

Figura\(\PageIndex{2}\): Diagrama de bloques de Laplace del sistema de control de retroalimentación de posición con filtrado paso bajo. (Copyright; autor vía fuente)

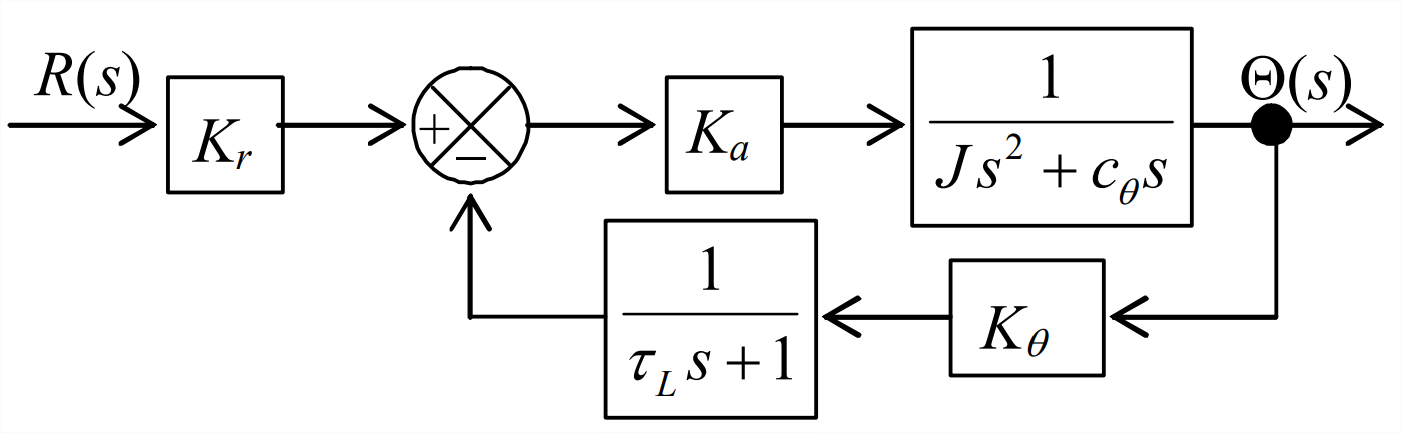
La manipulación algebraica de esta función de transferencia la arroja en las siguientes formas más útiles:

\[\frac{\Theta(s)}{R(s)}=\frac{K_{r} K_{a}}{J} \frac{s+1 / \tau_{L}}{s\left(s+\frac{c_{\theta}}{J}\right)\left(s+\frac{1}{\tau_{L}}\right)+\frac{K_{a} K_{\theta}}{J \tau_{L}}}=\frac{K_{r} K_{a}}{J} \frac{s+1 / \tau_{L}}{s^{3}+\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) s^{2}+\frac{c_{\theta}}{J} \frac{1}{\tau_{L}} s+\frac{K_{a} K_{\theta}}{J \tau_{L}}}\label{eqn:16.40} \]

Las dos formas algebraicas finales de la Ecuación\(\ref{eqn:16.40}\) pretenden agilizar tanto la evaluación por los criterios de Routh como por un análisis más general de la estabilidad en la Sección 16.4.

A partir de la función de transferencia Ecuación\(\ref{eqn:16.40}\) se pretende agilizar tanto la evaluación por los criterios de Routh siguiente como mediante un análisis más general de estabilidad en Sección, encontramos la ecuación característica:

\[\operatorname{Den}(p) \equiv a_{1} p^{3}+a_{2} p^{2}+a_{3} p+a_{4}=p^{3}+\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) p^{2}+\frac{c_{\theta}}{J} \frac{1}{\tau_{L}} p+\frac{K_{a} K_{\theta}}{J \tau_{L}}=0\label{eqn:16.41} \]

El primer conjunto de criterios de estabilidad positiva de Routh requiere que todos los coeficientes polinomiales sean distintos de cero y del mismo signo. Ya que\(a_1 = 1\), las siguientes desigualdades son condiciones necesarias pero no suficientes para una estabilidad positiva:

\[a_{2}=\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}>0, \quad a_{3}=\frac{c_{\theta}}{J} \frac{1}{\tau_{L}}>0, \text { and } \quad a_{4}=\frac{K_{a} K_{\theta}}{J \tau_{L}}>0\label{eqn:16.42} \]

La inercia rotacional\(J\) y la constante de tiempo de filtro\(\tau_{L}\) deben ser siempre constantes físicas positivas, por lo que las ecuaciones\(\ref{eqn:16.42}\) requieren para la estabilidad positiva que la constante de amortiguación\(c_{\theta}\) debe ser positiva, y que el producto de sensibilidades\(K_{a} K_{\theta}\) debe ser positiva. El requisito final de Routh para la estabilidad positiva de un sistema de ^tercer orden es la Ecuación\(\ref{eqn:16.38}\):

\[a_{2} \times a_{3}>a_{1} \times a_{4}>0 \Rightarrow\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) \frac{c_{\theta}}{J} \frac{1}{\tau_{L}}>\frac{K_{a} K_{\theta}}{J \tau_{L}}>0 \Rightarrow\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) \frac{c_{\theta}}{J}>\frac{K_{a} K_{\theta}}{J}>0\label{eqn:16.43a} \]

El factor común\(1 / \tau_{L}\) se eliminó para producir la forma final de la Ecuación\(\ref{eqn:16.43a}\).

Supongamos que los parámetros\(J\)\(c_{\theta}\),, y\(\tau_{L}\) son positivos y fijos, pero que el producto positivo de las sensibilidades\(K_{a} K_{\theta}\) es una ganancia de control que tenemos la capacidad de variar para modificar el rendimiento y/o la estabilidad del sistema de control. Será conveniente para el análisis continuado definir un símbolo especial que denota la fracción variable en la Ecuación\(\ref{eqn:16.43a}\) y expresar el requisito de estabilidad en términos de ese símbolo:

\[\frac{K_{a} K_{\theta}}{J} \equiv \Lambda \Rightarrow\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) \frac{c_{\theta}}{J}>\Lambda>0\label{eqn:16.43b} \]

La ecuación\(\ref{eqn:16.43b}\) establece límites de estabilidad superior e inferior para\(K_{a} K_{\theta} / J \equiv \Lambda\). Para ilustrar, expresemos numéricamente el criterio de estabilidad para algunos valores plausibles del sistema. Supongamos que la frecuencia de rotura circular del filtro paso bajo es\(\omega_{b} \equiv 1 / \tau_{L}= 300\) rad/s, correspondiente a la frecuencia de rotura cíclica\(f_{b}=\omega_{b} / 2 \pi=47.75\) Hz, un valor realista para un filtro de paso bajo utilizado en el control de un sistema mecánico. Supongamos también que los parámetros de la planta tienen valores tales que\(c_{\theta} / J=100\) s ^-1. Sustituir estas constantes en Ecuación\(\ref{eqn:16.43b}\) da el criterio: 40,000 s ⁻²\(>\Lambda>0\) para estabilidad positiva.

Para probar la corrección de los criterios de Routh, calculemos con MATLAB algunas respuestas de este sistema al\(\theta(0) \equiv \theta_{0}=0.1\) radián de condición inicial, con todos los demás CI cero y con entrada cero,\(r(t)=0\). Encontremos la respuesta del CI para estos tres casos:

Caso I\(\Lambda_{\mathrm{I}}=0.75 \times\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) \frac{c_{\theta}}{J}=30,000\) s ⁻²; esto debería dar una respuesta estable.

Caso II\(\Lambda_{\mathrm{II}} \equiv 1.00 \times\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) \frac{c_{\theta}}{J}=40,000\) s ^-2, el límite superior de la estabilidad; pero\(\Lambda\) se supone que es menor a 40,000 s ⁻² para la estabilidad (no igual a ella), entonces, ¿cuál será la naturaleza de esta respuesta?

Caso III\(\Lambda_{\mathrm{III}}=1.25 \times\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) \frac{c_{\theta}}{J}=50,000\) s ⁻²; esto debería dar una respuesta inestable.

Para resolver las respuestas IC de este sistema, adaptamos la Ecuación 16.1.2 a este problema. Un poco de álgebra nos lleva de la Ecuación 16.1.2 a la siguiente transformación de la respuesta IC:

\[\Theta(s)=\frac{\theta_{0}\left(a_{1} s^{2}+a_{2} s+a_{3}\right)}{a_{1} s^{3}+a_{2} s^{2}+a_{3} s+a_{4}}\label{eqn:16.44} \]

Las\(a_{k}\) constantes en Ecuación\(\ref{eqn:16.44}\) se definen en Ecuación\(\ref{eqn:16.42}\), y los parámetros numéricos se dan en el párrafo siguiente a la Ecuación\(\ref{eqn:16.43b}\). Para los valores numéricos de los Casos I, II y III descritos anteriormente, la expansión de fracción parcial de la Ecuación\(\ref{eqn:16.44}\) tiene la forma

\[\Theta(s)=\sum_{k=1}^{3} \frac{C_{k}}{s-p_{k}}=\frac{C_{1}}{s-p_{1}}+\frac{C_{2}}{s-p_{2}}+\frac{\overline{C_{2}}}{s-\overline{p_{2}}}\label{eqn:16.45} \]

en el que residuo\(C_1\) y polo\(p_1\) son constantes reales, con\(p_1\) negativas para los tres casos, y residuo\(C_2\) y polo\(p_{2} \equiv \sigma_{2}+j \omega_{2}\) son constantes complejas. Por lo tanto, a partir de las Ecuaciones 16.1.9 y 16.1.12, la respuesta temporal tiene la forma

\[\theta(t)=C_{1} e^{p_{1} t}+2\left|C_{2}\right| e^{\sigma_{2} t} \cos \left(\omega_{2} t+\angle C_{2}\right)\label{eqn:16.46} \]

El script M-file de MATLAB a continuación calcula las constantes de transform Equation\(\ref{eqn:16.45}\), usando la operación de residuo de MATLAB (ver tarea Problema 2.15), y calcula y traza la Ecuación de respuesta de tiempo\(\ref{eqn:16.46}\).

%Matlabdemo162.m

% Estabilidad de un rotor amortiguado con retroalimentación de posición filtrada de paso bajo

%Excitación con posición inicial

wb=300; CoVRJ=100; a2=Wb+COvrJ; A3=WB*COvrJ; LMUB=A2*covRj;

th0=0.1; t= 0:0. 0004:0 .16; formato corto e, figura, retención

Lm= [0.75 1 1.25] *Lmub;

para nc= 1:3;

A4=LM (nc) *wb;

num=th0* [1 a2 a3]; Den= [1 a2 a3 a4]; [C, p, k] =residuo (Num, Den);

disp ('Caso #, Lambda ='), disp ([nc Lm (nc)])

disp ('Polos p ='), disp (p. ') , disp ('Residuos C ='), disp (C. ')

sig=real (p (2)); wd=imag (p (2)); ABC=ABS (C (2)); ANC=ángulo (C (2));

TH=C (1) *exp (p (1) *t) +2*ABC*exp (sig*t). *cos (wd*t+ANC);

parcela (t, th, 'k')

final

grid, xlabel ('Tiempo t (seg) '), ylabel ('Posición\ theta (t) (radián)')

title ('Respuesta de un sistema de órdenes 3^r^d con diferentes ganancias de control')

El comando para ejecutar el archivo M y la salida alfanumérica resultante y la salida gráfica (después del uso de las características de edición de MATLAB para anotación y mejora gráfica) siguen:

>> MatlabDemo162

Parcela actual mantenida

Caso #, Lambda =

1 30000

Polos p =

-3.8302e+002 -8.4887e+000 +1.5305e+002i -8.4887e+000 -1.5305e+002i

Residuos C =

1.4354e-002 4.2823e-002 -2.0336e-002i 4.2823e-002 +2.0336e-002i

Caso #, Lambda =

2 40000

Polos p =

-4.0000e+002 -4.3965e-014 +1.7321e+002i -4.3965e-014 -1.7321e+002i

Residuos C =

1.5789e-002 4.2105e-002 -1.8232e-002i 4.2105e-002 +1.8232e-002i

Caso #, Lambda =

3 50000

Polos p =

-4.1484e+002 7.4222e+000 +1.9001e+002i 7.4222e+000 -1.9001e+002i

Residuos C =

1.6864e-002 4.1568e-002 -1.6786e-002i 4.1568e-002 +1.6786e-002i

Figura\(\PageIndex{3}\)^{: Respuesta de condición inicial de un sistema de control de salida-posición-retroalimentación del rotor con un filtro paso bajo de primer orden en la rama de retroalimentación.} (Copyright; autor vía fuente)

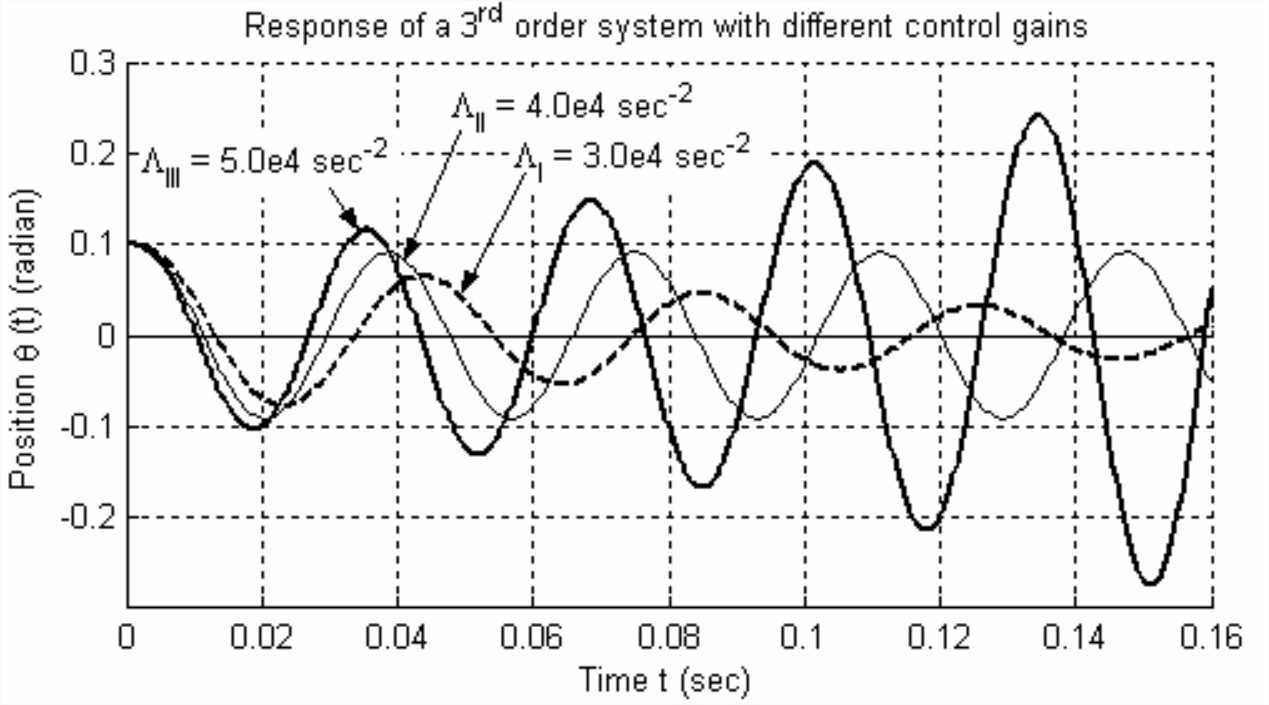
Para este sistema con tres polos, al menos un polo debe ser real. Para los Casos I, II, y III evaluados anteriormente, este polo real\(p_{1}\),, resulta ser fuertemente negativo, por lo que no contribuye a ninguna inestabilidad. El segundo polo,\(p_{2}\), es complejo, y el tercer polo es el conjugado del segundo. (La otra posibilidad para un sistema ^{de tercer} orden es que los tres polos puedan ser reales, pero las ganancias\(\Lambda\) utilizadas en este ejemplo lo excluyen). Para ganancia\(\Lambda_{\mathrm{I}}\),\(\operatorname{Re}\left(p_{2}\right)\) es negativo; en consecuencia, el sistema del Caso I es positivamente estable, como lo predice Routh, Ecuación\(\ref{eqn:16.43b}\). Para ganancia\(\Lambda_{\mathrm{III}}\),\(\operatorname{Re}\left(p_{2}\right)\) es positivo; en consecuencia, el sistema Caso III es inestable, también como lo predijo Routh. La ganancia\(\Lambda_{\mathrm{II}}\) está en el límite superior entre la estabilidad positiva y negativa, de acuerdo con Routh, y la salida alfanumérica anterior lo muestra\(\operatorname{Re}\left(p_{2}\right)=0\). (El número minúsculo calculado, −4.4e−14, es distinto de cero debido al error de redondeo; la comparación de este número con los valores de los otros polos muestra que efectivamente es cero). Vemos a partir de la Figura\(\PageIndex{3}\) que la respuesta temporal asociada al Caso II es una sinusoide pura, no amortiguada; la respuesta está acotada, por lo tanto no es inestable, pero no es exponencialmente estable, es decir, no decae a cero.

El sistema de control de Figuras\(\PageIndex{1}\) y\(\PageIndex{2}\) cuenta con dos subsistemas dinámicos principales: el rotor amortiguado con función de transferencia\(1 /\left[s\left(J s+c_{\theta}\right)\right]\); y el filtro de paso bajo con función de transferencia\(1 /\left(\tau_{L} s+1\right)\). Cada uno de estos subsistemas pasivos por sí mismo disipa la energía, es decir, actúa como un sumidero de energía, y es positivamente estable. Pero el sistema completo es claramente capaz de ser inestable. El sistema completo incluye una fuente de energía, el actuador de momento, y por lo tanto se dice que está activo. Cualquier sistema que incluya retroalimentación y una fuente de energía es potencialmente capaz de ser inestable.

Observe que los criterios de Routh esencialmente nos dicen sólo que un sistema es estable o inestable, la naturaleza de la estabilidad en un sentido absoluto. No nos dicen el tipo de respuesta (monótona-exponencial u oscilatoria) ni el grado de estabilidad (esencialmente, las magnitudes de las partes reales de los polos de función de transferencia), lo que también se conoce como estabilidad relativa. El método introducido en la siguiente sección encuentra la estabilidad relativa.