3.2: Vector de Poynting

En esta sección, utilizamos el teorema de Poynting (Sección 3.1) para confirmar la interpretación del vector Poynting

\[\boxed{ {\bf S} \triangleq {\bf E} \times {\bf H} } \nonumber \]

como la densidad de potencia espacial (unidades base SI de W/m\(^2\)) y la dirección del flujo de potencia.

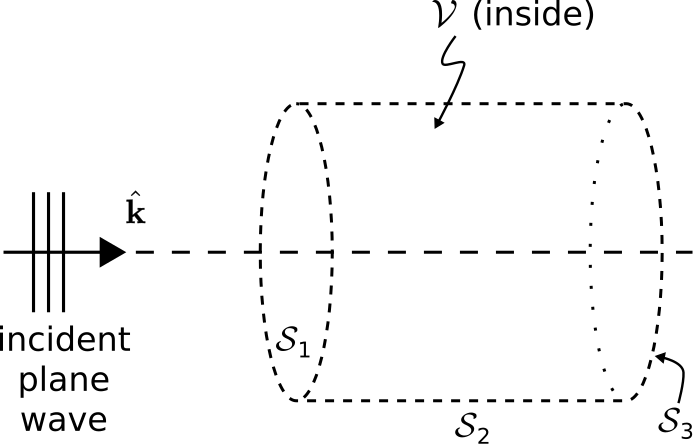
La figura\(\PageIndex{1}\) muestra una onda plana uniforme incidente en una región homogénea y sin pérdidas\(\mathcal{V}\) definida por el cilindro derecho cerrado\(\mathcal{S}\). El eje del cilindro está alineado a lo largo de la dirección de propagación\(\hat{\bf k}\) de la onda plana. Los extremos del cilindro son planos y perpendiculares a\(\hat{\bf k}\).

Figura\(\PageIndex{1}\): Onda plana uniforme incidente en una región delimitada por la superficie cilíndrica\(\mathcal{S}\). (CC BY-SA 4.0; C. Wang)

Ahora vamos a aplicar el teorema de Poynting:

\[P_{net,in} = P_{\Omega} + \frac{\partial}{\partial t} W_e + \frac{\partial}{\partial t} W_m \nonumber \]

Dado que la región es sin pérdidas,\(P_{\Omega}=0\). Presumiendo que no hay otros campos eléctricos o magnéticos,\(W_e\) y también\(W_m\) debe ser cero. En consecuencia,\(P_{net,in}=0\). Sin embargo, esto no quiere decir que no haya un poder fluyendo hacia adentro\(\mathcal{V}\). En cambio,\(P_{net,in}=0\) simplemente indica que la potencia neta que fluye hacia\(\mathcal{V}\) adentro es cero. Por lo tanto, podríamos expresar el resultado para el escenario actual de la siguiente manera:

\[P_{net,in} = P_{in}-P_{out} = 0 \label{m0122_ePB} \]

donde\(P_{in}\) e\(P_{out}\) indicar el flujo de energía explícitamente dentro y explícitamente fuera de\(\mathcal{V}\) como cantidades separadas.

Procediendo, ignoremos lo que sabemos sobre el flujo de energía en ondas planas, y en su lugar veamos a dónde nos lleva el teorema de Poynting. Aquí,

\[P_{net,in} \triangleq -\oint_{\mathcal{S}} \left( {\bf E} \times {\bf H} \right) \cdot d{\bf s} = 0 \nonumber \]

La superficie\(\mathcal{S}\) consta de tres lados: Los dos extremos planos, y la superficie curva que los conecta. Vamos a referirnos a estos lados como\(\mathcal{S}_1\),\(\mathcal{S}_2\), y\(\mathcal{S}_3\), de izquierda a derecha como se muestra en la Figura\(\PageIndex{1}\). Entonces,

\[\begin{aligned} -&\int_{\mathcal{S}_1} \left( {\bf E} \times {\bf H} \right) \cdot d{\bf s} \\ \nonumber -&\int_{\mathcal{S}_2} \left( {\bf E} \times {\bf H} \right) \cdot d{\bf s} \\ \nonumber -&\int_{\mathcal{S}_3} \left( {\bf E} \times {\bf H} \right) \cdot d{\bf s} = 0\end{aligned} \nonumber \]

En la superficie curva\(\mathcal{S}_2\),\(d{\bf s}\) está en todas partes perpendicular a\({\bf E} \times {\bf H}\) (es decir, perpendicular a\(\hat{\bf k}\)). Por lo tanto, la segunda integral es igual a cero. En el extremo izquierdo\(\mathcal{S}_1\), el elemento de superficie diferencial orientado hacia afuera\(d{\bf s} = -\hat{\bf k}ds\). En el extremo derecho\(\mathcal{S}_3\),\(d{\bf s} = +\hat{\bf k}ds\). Nos quedamos con:

\[\begin{aligned} &\int_{\mathcal{S}_1} \left( {\bf E} \times {\bf H} \right) \cdot \hat{\bf k}ds \\ \nonumber -&\int_{\mathcal{S}_3} \left( {\bf E} \times {\bf H} \right) \cdot \hat{\bf k}ds = 0\end{aligned} \nonumber \]

Compárelo con la Ecuación\ ref {M0122_EPb}. Ya que\(\hat{\bf k}\) es, por definición, la dirección en la que\({\bf E} \times {\bf H}\) apunta, la primera integral debe ser\(P_{in}\) y la segunda integral debe ser\(P_{out}\). Por lo tanto,

\[P_{in} = \int_{\mathcal{S}_1} \left( {\bf E} \times {\bf H} \right) \cdot \hat{\bf k}ds \nonumber \]

y se deduce que la magnitud y dirección de\({\bf E}\times{\bf H}\), que reconocemos como el vector Poynting, son densidad de potencia espacial y dirección del flujo de potencia, respectivamente.

El vector Poynting lleva el nombre del físico inglés J.H. Poynting, uno de los co-descubridores del concepto. El hecho de que este vector apunte en la dirección del flujo de potencia, y por lo tanto sea también un “vector apuntador”, es simplemente una coincidencia notable.

Lectura adicional:

• “Poynting vector” en Wikipedia.