5.10: Reflexión TM en medios no magnéticos
- Page ID
- 83771
La figura\(\PageIndex{1}\) muestra una onda plana uniforme TM incidente en el límite plano entre dos regiones de material semi-infinitas.
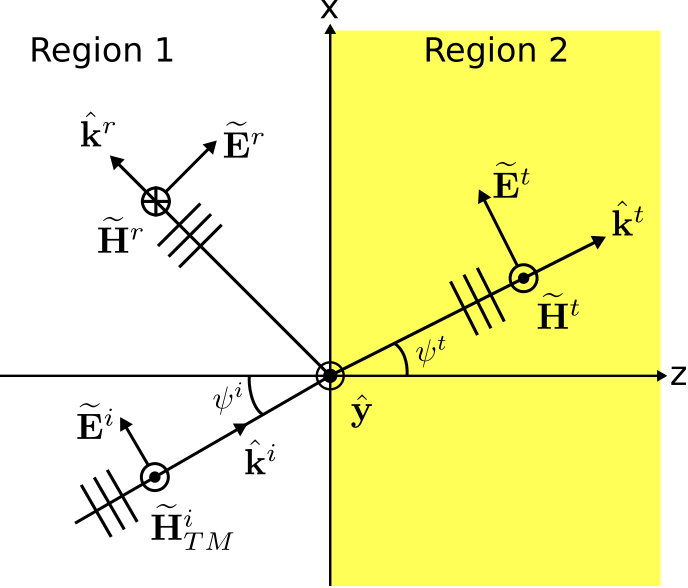
En este caso, el coeficiente de reflexión viene dado por:
\[\Gamma_{TM} = \frac{-\eta_1\cos\psi^i+\eta_2\cos\psi^t}{+\eta_1\cos\psi^i + \eta_2\cos\psi^t} \label{m0172_eGTM} \]
donde\(\psi^i\) y\(\psi^t\) son los ángulos de incidencia y transmisión (refracción), respectivamente;\(\eta_1\) y\(\eta_2\) son las impedancias de onda en las Regiones 1 y 2, respectivamente. Muchos materiales de interés práctico son no magnéticos; es decir, tienen permeabilidad que no es significativamente diferente de la permeabilidad del espacio libre. En esta sección, consideramos el comportamiento del coeficiente de reflexión para esta clase de materiales.
Para comenzar, recuerda la forma general de la ley de Snell:
\[\sin{\psi^t} = \frac{\beta_1}{\beta_2}\sin\psi^i \label{m0172_eSLNM} \]
En medios no magnéticos, las permeabilidades\(\mu_1\) y\(\mu_2\) se asumen iguales a\(\mu_0\). Así:
\[\frac{\beta_1}{\beta_2} = \frac{\omega\sqrt{\mu_1\epsilon_1}}{\omega\sqrt{\mu_2\epsilon_2}} = \sqrt{\frac{\epsilon_1}{\epsilon_2}} \nonumber \]
Dado que la permitividad se\(\epsilon\) puede expresar como\(\epsilon_0\) veces la permitividad relativa\(\epsilon_r\), podemos reducir aún más a:
\[\frac{\beta_1}{\beta_2} = \sqrt{\frac{\epsilon_{r1}}{\epsilon_{r2}}} \nonumber \]
Ahora la Ecuación\ ref {M0172_ESLNm} se reduce a:
\[\sin{\psi^t} = \sqrt{\frac{\epsilon_{r1}}{\epsilon_{r2}}} \sin\psi^i \nonumber \]
A continuación, tenga en cuenta que para cualquier valor\(\psi\), se puede escribir coseno en términos de seno de la siguiente manera:
\[\cos{\psi} = \sqrt{1-\sin^2{\psi}} \nonumber \]
Por lo tanto,
\[\cos{\psi^t} = \sqrt{1-\frac{\epsilon_{r1}}{\epsilon_{r2}} \sin^2\psi^i } \label{m0172_eCpt} \]
También observamos que en medios no magnéticos
\[\begin{aligned} \eta_1 &= \sqrt{\frac{\mu_1}{\epsilon_1}} = \sqrt{\frac{\mu_0}{\epsilon_{r1}\epsilon_0}} = \frac{\eta_0}{\sqrt{\epsilon_{r1}}} \\ \eta_2 &= \sqrt{\frac{\mu_2}{\epsilon_2}} = \sqrt{\frac{\mu_0}{\epsilon_{r2}\epsilon_0}} = \frac{\eta_0}{\sqrt{\epsilon_{r2}}} \end{aligned} \nonumber \]
donde\(\eta_0\) está la impedancia de onda en el espacio libre. Haciendo sustituciones en la Ecuación\ ref {M0172_EGTM}, obtenemos:
\[\Gamma_{TM} = \frac{-\left(\eta_0/\sqrt{\epsilon_{r1}}\right)\cos\psi^i + \left(\eta_0/\sqrt{\epsilon_{r2}}\right)\cos\psi^t} {+\left(\eta_0/\sqrt{\epsilon_{r1}}\right)\cos\psi^i + \left(\eta_0/\sqrt{\epsilon_{r2}}\right)\cos\psi^t} \nonumber \]
Multiplicando numerador y denominador por\(\sqrt{\epsilon_{r2}}/\eta_0\), obtenemos:
\[\Gamma_{TM} = \frac{-\sqrt{\epsilon_{r2}/\epsilon_{r1}}\cos\psi^i + \cos\psi^t} {+\sqrt{\epsilon_{r2}/\epsilon_{r1}}\cos\psi^i + \cos\psi^t} \nonumber \]
Sustituyendo la ecuación\ ref {m0172_Ecpt}, obtenemos:
\[\Gamma_{TM} = \frac{-\sqrt{\epsilon_{r2}/\epsilon_{r1}}\cos\psi^i+\sqrt{1-\left(\epsilon_{r1}/\epsilon_{r2}\right)\sin^2\psi^i}} {+\sqrt{\epsilon_{r2}/\epsilon_{r1}}\cos\psi^i+\sqrt{1-\left(\epsilon_{r1}/\epsilon_{r2}\right)\sin^2\psi^i}} \nonumber \]
Esta expresión tiene la ventaja de que ahora es enteramente en términos de\(\psi^i\), sin necesidad de calcular primero\(\psi^t\).
Finalmente, multiplicando numerador y denominador por\(\sqrt{\epsilon_{r2}/\epsilon_{r1}}\), obtenemos:
\[\boxed{ \Gamma_{TM} = \frac{-\left(\epsilon_{r2}/\epsilon_{r1}\right)\cos\psi^i+\sqrt{\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i}} {+\left(\epsilon_{r2}/\epsilon_{r1}\right)\cos\psi^i+\sqrt{\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i}} } \label{m0172_eGTMi} \]
Usando la Ecuación\ ref {M0172_EGTMI}, podemos ver fácilmente cómo diferentes combinaciones de material afectan el coeficiente de reflexión. Primero, observamos que cuando\(\epsilon_{r1}=\epsilon_{r2}\) (es decir, mismos medios a ambos lados de la frontera),\(\Gamma_{TM}=0\) como se esperaba. Cuando\(\epsilon_{r1}>\epsilon_{r2}\) (por ejemplo, onda viajando en vidrio hacia el aire), vemos que es posible que sea negativo, lo que hace que sea\(\Gamma_{TM}\) de valor complejo.\(\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i\) Esto da como resultado una reflexión interna total, y se aborda en otra sección. Cuando\(\epsilon_{r1}<\epsilon_{r2}\) (por ejemplo, la ola que viaja en el aire hacia el vidrio), vemos que siempre\(\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i\) es positivo, por lo que siempre\(\Gamma_{TM}\) es de valor real.
Sigamos con la\(\epsilon_{r1}<\epsilon_{r2}\) condición. La figura\(\PageIndex{2}\) muestra\(\Gamma_{TM}\) graficamente para diversas combinaciones de medios en todos los ángulos de incidencia posibles de 0 (incidencia normal) a\(\pi/2\) (incidencia de pastoreo).
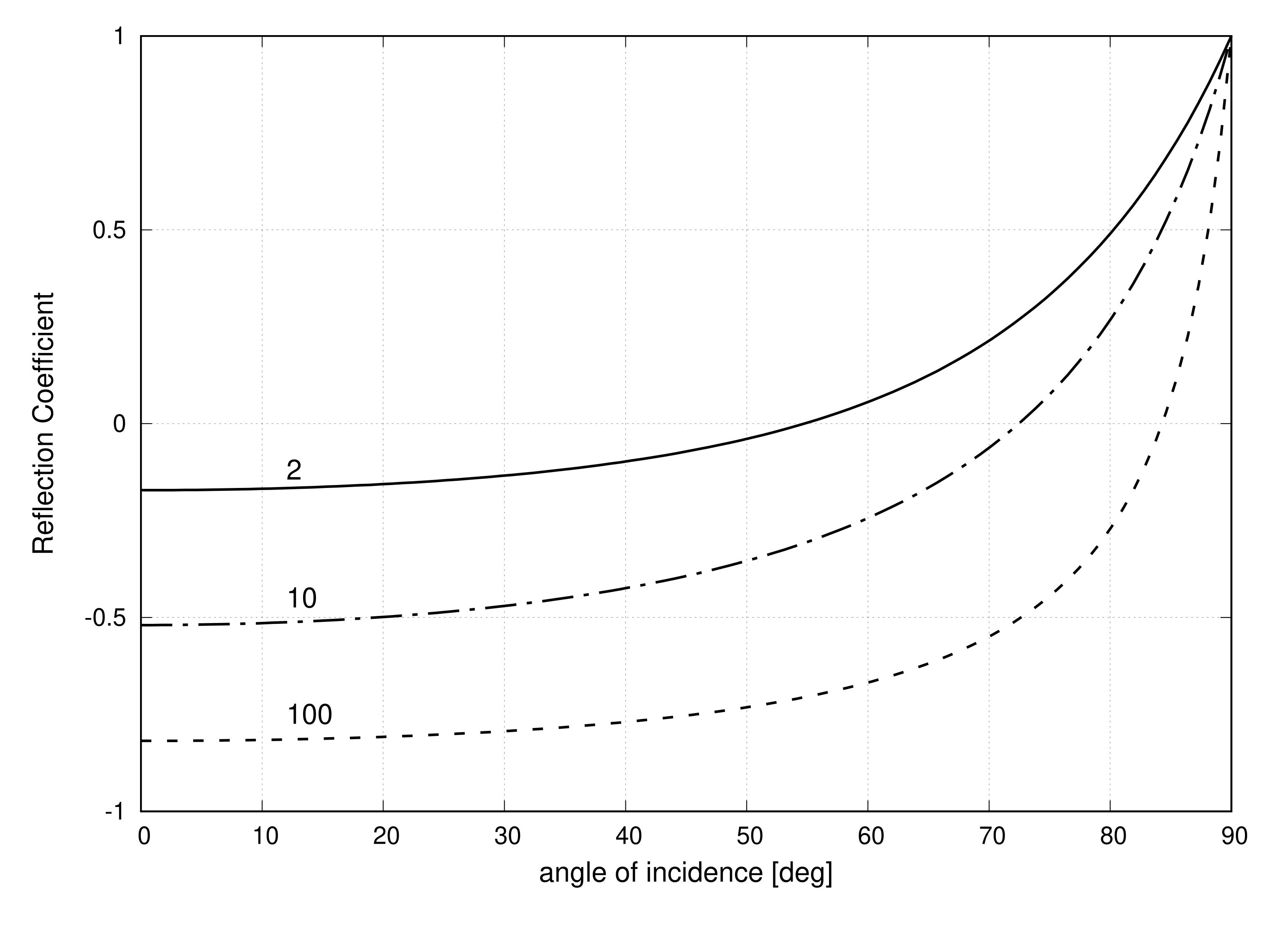
Observamos:
En medios no magnéticos con\(\epsilon_{r1}<\epsilon_{r2}\),\(\Gamma_{TM}\) es de valor real y se incrementa de un valor negativo para la incidencia normal a\(+1\) medida que se\(\psi^i\) aproxima a la incidencia de pastoreo.
Tenga en cuenta que en cualquier ángulo particular de incidencia,\(\Gamma_{TM}\) las tendencias hacia\(-1\) as\(\epsilon_{r2}/\epsilon_{r1}\to\infty\). En este sentido, el comportamiento del componente TM es similar al del componente TE. En otras palabras: As\(\epsilon_{r2}/\epsilon_{r1}\to\infty\), el resultado tanto para los componentes TE como TM son cada vez más similares al resultado que obtendríamos para un conductor perfecto en la Región 2.
También tenga en cuenta que cuando\(\epsilon_{r1}<\epsilon_{r2}\),\(\Gamma_{TM}\) los cambios firman de negativo a positivo a medida que aumenta el ángulo de incidencia de 0 a\(\pi/2\). Este comportamiento es bastante diferente al del componente TE, que siempre es negativo para\(\epsilon_{r1}<\epsilon_{r2}\). El ángulo de incidencia en el que\(\Gamma_{TM}=0\) se conoce como ángulo de Brewster, al que asignamos el símbolo\(\psi^i_B\). Así:
\[\boxed{ \psi^i_B \triangleq \psi^i ~~\mbox{at which}~~ \Gamma_{TM}=0 } \nonumber \]
En la discusión que sigue, aquí está el punto clave a tener en cuenta:
El ángulo de Brewster\(\psi^i_B\) es el ángulo de incidencia en el que\(\Gamma_{TM}=0\).
El ángulo de Brewster también se conoce como el ángulo de polarización. La motivación para el término “ángulo polarizador” se demuestra en la Figura\(\PageIndex{3}\).
En esta figura, una onda de avión es incidente con\(\psi^i=\psi^i_B\). La onda puede contener componentes TE y TM en cualquier combinación. Aplicando el principio de superposición, podemos considerar estos componentes por separado. El componente TE de la onda incidente se dispersará como ondas reflejadas y transmitidas que también son TE. Sin embargo\(\psi^i=\psi^i_B\),\(\Gamma_{TM}=0\) cuando, entonces el componente TM de la onda transmitida será TM, pero el componente TM de la onda reflejada será cero. Así, la onda reflejada total (TE\(+\) TM) será puramente TE, independientemente del componente TM de la onda incidente. Este principio puede explotarse para suprimir el componente TM de una onda que tiene componentes TE y TM. Este método se puede utilizar para aislar los componentes TE y TM de una onda.
Derivación de una fórmula para el ángulo de Brewster
El ángulo de Brewster para cualquier combinación particular de medios no magnéticos se puede determinar de la siguiente manera. \(\Gamma_{TM}=0\)cuando el numerador de la Ecuación\ ref {M0172_EGTMI} es igual a cero, entonces:
\[-R\cos\psi^i_B+\sqrt{R-\sin^2\psi^i_B} = 0 \nonumber \]
donde hemos hecho la sustitución\(R\triangleq\epsilon_{r2}/\epsilon_{r1}\) para mejorar la claridad. Al mover el segundo término al lado derecho de la ecuación y cuadrar ambos lados, obtenemos:
\[R^2\cos^2\psi^i_B = R-\sin^2\psi^i_B \nonumber \]
Ahora empleando una identidad trigonométrica en el lado izquierdo de la ecuación, obtenemos:
\[\begin{aligned} R^2\left(1-\sin^2\psi^i_B\right) &= R-\sin^2\psi^i_B \\ R^2 -R^2 \sin^2\psi^i_B &= R-\sin^2\psi^i_B \\ \left(1-R^2\right)\sin^2\psi^i_B &= R - R^2 \end{aligned} \nonumber \]
y finalmente
\[\sin\psi^i_B = \sqrt{ \frac{ R - R^2 }{ 1-R^2 } } \label{m0172_eBA1} \]
A pesar de que esta ecuación consigue hacer el trabajo, es posible simplificar aún más. Tenga en cuenta que la Ecuación\ ref {M0172_EbA1} puede interpretarse como una descripción del triángulo rectángulo que se muestra en la Figura\(\PageIndex{4}\).
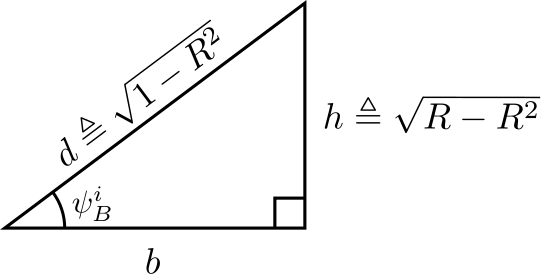
En la figura, hemos identificado la longitud\(h\) del lado vertical y la longitud\(d\) de la hipotenusa como:
\[\begin{aligned} h &\triangleq \sqrt{R-R^2} \\ d &\triangleq \sqrt{1-R^2}\end{aligned} \nonumber \]
Por lo tanto,\(b\) la longitud del lado horizontal es
\[b = \sqrt{d^2-h^2} = \sqrt{1-R} \nonumber \]
Posteriormente, observamos
\[\tan\psi^i_B = \frac{h}{b} = \frac{\sqrt{R-R^2}}{\sqrt{1-R}} = \sqrt{R} \nonumber \]
Así, hemos encontrado
\[\boxed{ \tan\psi^i_B = \sqrt{\frac{\epsilon_{r2}}{\epsilon_{r1}}} } \label{m0172_eBA} \]
Una onda plana incide desde el aire en el límite plano con una región de vidrio. El vidrio exhibe una permitividad relativa de 2.1. La onda incidente contiene componentes TE y TM. ¿En qué ángulo de incidencia\(\psi^i\) la onda reflejada será puramente TE?
Solución
Usando la ecuación\ ref {M0172_EBA}:
\[\tan\psi^i_B = \sqrt{\frac{\epsilon_{r2}}{\epsilon_{r1}}} = \sqrt{\frac{2.1}{1}} \cong 1.449 \nonumber \]
Por lo tanto, el ángulo de Brewster es\(\psi^i_B\cong 55.4^{\circ}\). Este es el ángulo\(\psi^i\) en el que\(\Gamma_{TM}=0\). Por lo tanto, cuando\(\psi^i=\psi^i_B\), la onda reflejada no contiene ningún componente TM y por lo tanto debe ser puramente TE.