5.12: Ondas evanescentes

Consideremos la situación que se muestra en la Figura$\PageIndex{1}$:

Figura$\PageIndex{1}$: Onda plana uniforme que incide oblicuamente en el límite plano entre dos regiones de material semiinfinitas. Aquí$\mu_{r 1} \epsilon_{r 1}>\mu_{r 2} \epsilon_{r 2}$ y$\psi^i > \psi^i_c$. (CC BY-SA 4.0; C. Wang)

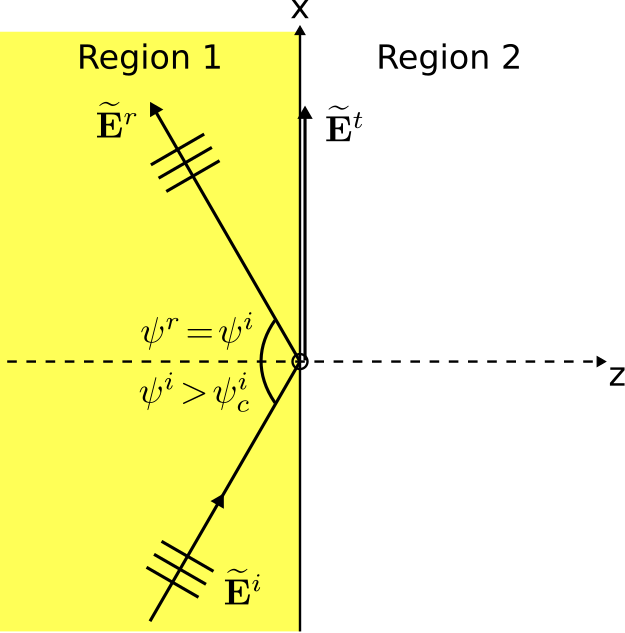
Una onda plana uniforme que incide oblicuamente en el límite plano entre dos regiones de material semi-infinitas, y la reflexión interna total ocurre porque el ángulo de incidencia$\psi^i$ es mayor que el ángulo crítico

$$\psi^i_c = \arcsin\sqrt{\frac{\mu_{r2}\epsilon_{r2}}{\mu_{r1}\epsilon_{r1}}} \label{m0170_eCA}$$

Por lo tanto, el coeficiente de reflexión es de valor complejo con magnitud igual a 1 y fase que depende de la polarización y de los parámetros constitutivos de los medios.

La reflexión total de la onda incidente parece contradecir las condiciones límite que requieren que los componentes tangenciales de los campos eléctrico y magnético sean continuos a través del límite. ¿Cómo pueden estos componentes de los campos ser continuos a través del límite si no se transmite energía a través del límite? Debe haber un campo en el lado opuesto del límite, pero —de alguna manera— debe tener potencia cero. Para darle sentido a esto, intentemos encontrar una solución para el campo transmitido.

Comenzamos por postular un ángulo de transmisión de valor complejo$\psi^{tc}$. Aunque el concepto de ángulo de valor complejo puede parecer contrario a la intuición, existe un soporte matemático para este concepto. Por ejemplo, considere las conocidas identidades trigonométricas:

$$\begin{align} \sin\theta &= \frac{1}{j2}\left( e^{j\theta} - e^{-j\theta} \right) \label{m0170_eSI} \\ \cos\theta &= \frac{1}{2}\left( e^{j\theta} + e^{-j\theta} \right) \label{m0170_eSC}\end{align}$$

Estas identidades nos permiten calcular valores para seno y coseno incluso cuando$\theta$ es de valor complejo. Se puede concluir que el seno y el coseno de un ángulo de valor complejo existen, aunque los resultados también pueden ser de valor complejo.

Con base en las evidencias establecidas hasta el momento, presumimos que$\psi^{tc}$ se comporta de la siguiente manera:

$$\begin{align} \psi^{tc} &\triangleq \psi^t~\mbox{,} ~~~ ~~~ ~~~\psi^i<\psi^i_c \label{m0170_eptc1} \\ \psi^{tc} &\triangleq \pi/2~\mbox{,} ~~~ ~~~ \psi^i=\psi^i_c \label{m0170_eptc2} \\ \psi^{tc} &\triangleq \pi/2+j\psi''~\mbox{,} ~~~ \psi^i>\psi^i_c \label{m0170_eptc3}\end{align}$$

En otras palabras,$\psi^{tc}$ es idéntico a$\psi^t$ for$\psi^i\le\psi^i_c$, pero cuando se produce la reflexión interna total, presumimos que la parte real de$\psi^{tc}$ permanece fija (paralela al límite) y que$j\psi''$ emerge un componente imaginario para satisfacer las condiciones límite.

Para mayor claridad, asignemos la variable$\psi'$ para representar la parte real de$\psi^{tc}$ en Ecuaciones\ ref {m0170_eptc1} -\ ref {m0170_eptc3}. Entonces podemos referirnos a los tres casos usando una sola expresión de la siguiente manera:

$$\psi^{tc} = \psi' + j\psi'' \nonumber$$

Ahora utilizamos una conocida identidad trigonométrica de la siguiente manera:

$$\begin{align} \sin{\psi^{tc}} &= \sin{\left(\psi' + j\psi''\right)} \\ &= \sin{\psi'}\cos{j\psi''} + \cos{\psi'}\sin{j\psi''} \label{m0170_eSptc}\end{align}$$

Usando la ecuación\ ref {m0170_ESC}, encontramos:

$$\begin{aligned} \cos{j\psi''} &= \frac{1}{2}\left( e^{j\left(j\psi''\right)} + e^{-j\left(j\psi''\right)} \right) \\ &= \frac{1}{2}\left( e^{-\psi''} + e^{+\psi''} \right) \\ &= \cosh{\psi''}\end{aligned} \nonumber$$

En otras palabras, el coseno de$j\psi''$ es simplemente el coseno hiperbólico (“$\cosh$”) de$\psi''$. Curiosamente,$\cosh$ de un argumento de valor real es de valor real, por lo que$\cos{j\psi''}$ es de valor real.

Usando la ecuación\ ref {M0170_ESI}, encontramos:

$$\begin{align} \sin{j\psi''} &= \frac{1}{j2}\left( e^{j\left(j\psi''\right)} - e^{-j\left(j\psi''\right)} \right) \\ &= \frac{1}{j2}\left( e^{-\psi''} - e^{+\psi''} \right) \\ &= j\frac{1}{2}\left( e^{+\psi''} - e^{-\psi''} \right) \\ &= j\sinh{\psi''}\end{align} \nonumber$$

En otras palabras, el seno de$j\psi''$ es$j$ veces seno hiperbólico (“$\sinh$”) de$\psi''$. Ahora tenga en cuenta que$\sinh$ de un argumento de valor real es de valor real, por lo que$\sin{j\psi''}$ es de valor imaginario.

Usando estos resultados, encontramos que la Ecuación\ ref {M0170_ESPTC} puede escribirse de la siguiente manera:

$$\sin{\psi^{tc}} = \sin{\psi'}\cosh{\psi''} + j\cos{\psi'}\sinh{\psi''} \label{m0170_eStc2}$$

Usando precisamente el mismo enfoque, encontramos:

$$\cos{\psi^{tc}} = \cos{\psi'}\cosh{\psi''} - j\sin{\psi'}\sinh{\psi''} \label{m0170_eCtc2}$$

Antes de continuar, asegurémonos de que las Ecuaciones\ ref {M0170_Estc2} y\ ref {M0170_ECTC2} exhiban el comportamiento esperado antes del inicio de la reflexión interna total. Para$\psi^i<\psi^i_c$,$\psi'=\psi^t$ y$\psi''=0$. En este caso,$\sinh\psi''=0$,$\cosh\psi''=1$, y Ecuaciones\ ref {M0170_ESTC2} y\ ref {M0170_ECTC2} rendimiento

$$\begin{aligned} \sin{\psi^{tc}} &= \sin{\psi^t} \\ \cos{\psi^{tc}} &= \cos{\psi^t}\end{aligned} \nonumber$$

como se esperaba.

Cuando la reflexión interna total está vigente,$\psi^i>\psi^i_c$, entonces$\psi'=\pi/2$. En este caso, las Ecuaciones\ ref {M0170_ESTC2} y\ ref {M0170_ECTC2} rinden

$$\begin{align} \sin{\psi^{tc}} &= \cosh{\psi''} \\ \cos{\psi^{tc}} &= -j\sinh{\psi''}\end{align} \nonumber$$

Consideremos ahora qué significa esto para el campo en la Región 2. De acuerdo con el formalismo adoptado en secciones anteriores, la propagación de componentes de onda en esta región se describe por el factor$e^{-j{\bf k}^t\cdot{\bf r}}$ donde

$$\begin{align} {\bf k}^t &= \beta_2\hat{\bf k}^t \nonumber \\ &= \beta_2\left( \hat{\bf x}\sin\psi^{tc} + \hat{\bf z}\cos\psi^{tc} \right) \end{align} \nonumber$$

y

$${\bf r} = \hat{\bf x}x + \hat{\bf y}y + \hat{\bf z}z \nonumber$$

por lo

$$\begin{align} {\bf k}^t\cdot{\bf r} &= \left(\beta_2\sin\psi^{tc}\right)x + \left(\beta_2\cos\psi^{tc}\right)z \nonumber \\ &= \left(\beta_2\cosh{\psi''}\right)x + \left(-j\beta_2\sinh{\psi''}\right)z \end{align} \nonumber$$

Por lo tanto, la onda en la Región 2 se propaga según

$$\begin{aligned} e^{-j{\bf k}^t\cdot{\bf r}} &= e^{-j\left(\beta_2\cosh{\psi''}\right)x}e^{-\left(\beta_2\sinh{\psi''}\right)z} \label{m0170_eEv1}\end{aligned}$$

Tenga en cuenta que las constantes$\beta_2\cosh{\psi''}$ y$\beta_2\sinh{\psi''}$ son tanto reales como positivas. Por lo tanto, la Ecuación\ ref {M0170_EEV1} describe una onda que se propaga en la$+\hat{\bf x}$ dirección, pero que no es uniforme. Específicamente, la magnitud del campo transmitido disminuye exponencialmente con el aumento$z$; es decir, máximo en el límite, acercándose asintóticamente a cero al aumentar la distancia desde el límite. Esta onda es diferente a las ondas incidentes o reflejadas (ambas ondas planas uniformes), y es diferente a la onda transmitida en el$\psi^i<\psi^i_c$ caso (también una onda plana uniforme). La onda transmitida que hemos derivado en el$\psi^i>\psi^i_c$ caso da la impresión de estar de alguna manera unida al límite, y así puede describirse como una onda superficial. Sin embargo, en este caso tenemos un tipo particular de onda superficial, conocida como onda evanescente. Resumiendo:

Cuando se produce la reflexión interna total, el campo transmitido es una onda evanescente; es decir, una onda superficial que no transmite energía y cuya magnitud decae exponencialmente al aumentar la distancia hacia la Región 2.

En este punto, podríamos hacer cumplir la condición de “coincidencia de fases” en el límite, lo que nos llevaría a una nueva versión de la ley de Snell que nos permitiría resolver$\psi''$ en términos$\psi^i$ y propiedades constitutivas de los medios de comunicación que comprenden las Regiones 1 y 2. Posteriormente se pudieron determinar los valores para la propagación de fase y las constantes de atenuación para la onda evanescente. Basta decir que la magnitud del campo evanescente se vuelve insignificante más allá de unas pocas longitudes de onda del límite.

Por último, volvemos a la característica más extraña de este campo: Actúa como una ola, pero no transmite poder. Este campo existe únicamente para hacer cumplir las condiciones de límite electromagnético en el límite, y no existe independientemente del campo incidente y reflejado. El siguiente experimento mental puede proporcionar algunas ideas adicionales.

En este experimento, un láser ilumina un límite plano entre dos regiones materiales, con condiciones tales que se produce una reflexión interna total. Así, toda la potencia incidente se refleja, y existe una onda evanescente en el lado opuesto del límite. A continuación, se apaga el láser. Toda la luz incidente en el límite se refleja desde el límite y continúa propagándose hasta el infinito, incluso después de que la luz ya no incida en el límite. En contraste, la onda evanescente desaparece en el momento en que la luz láser deja de iluminar el límite. En otras palabras, el campo evanescente no continúa propagándose a lo largo del límite hasta el infinito. La razón de esto es simplemente que no hay poder —por lo tanto, no hay energía— en la onda evanescente.