7.2: Microstrip Line Redux
- Page ID
- 83644
Una línea de transmisión de microcinta consiste en una traza metálica estrecha separada de un plano de tierra metálico por una losa de material dieléctrico, como se muestra en la Figura\(\PageIndex{1}\). Esta es una forma natural de implementar una línea de transmisión en una placa de circuito impreso y, por lo tanto, representa una gama importante y amplia de aplicaciones. El lector debe ser consciente de que la microcinta es distinta de la línea de cinta, que es un tipo distinto de línea de transmisión; consulte “Lectura adicional” al final de esta sección para la desambiguación de estos términos.
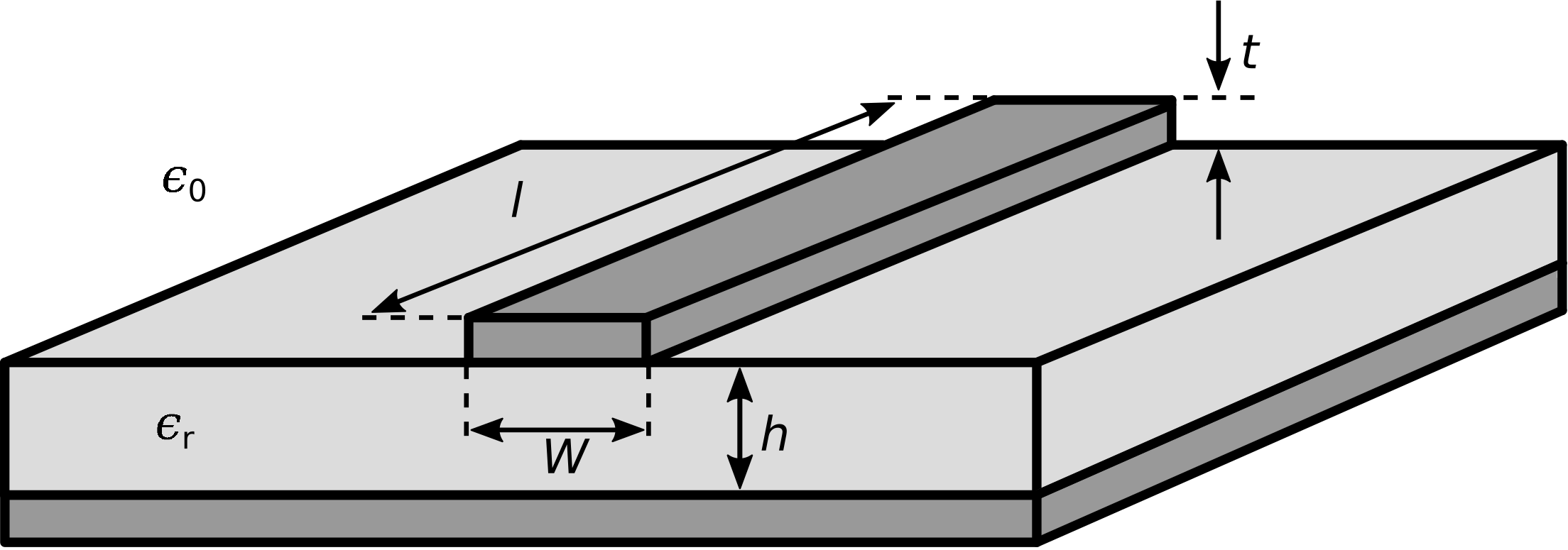
Una línea de microcinta es de un solo extremo 1 en el sentido de que la geometría del conductor es asimétrica y el conductor, es decir, el plano de tierra, también sirve normalmente como tierra para la fuente y la carga.
El material espaciador es típicamente un material dieléctrico de baja pérdida que tiene una permeabilidad aproximadamente igual a la del espacio libre (\(\mu \approx \mu_0\)) y una permitividad relativa\(\epsilon_r\) en el intervalo de 2 a aproximadamente 10 o así.
La estructura de una línea de microcinta es similar a la de una guía de ondas de placa paralela (Sección 6.6), con la obvia diferencia de que una de las “placas” tiene longitud finita en la dirección perpendicular a la dirección de propagación. A pesar de esta diferencia, la guía de ondas de placa paralela proporciona información útil sobre el funcionamiento de la línea de microcinta. La línea de microcinta casi siempre se opera por debajo de la frecuencia de corte de todos menos el\(_0\) modo TM, cuya frecuencia de corte es cero. Esto garantiza que solo el\(_0\) modo TM puede propagarse. El\(_0\) modo TM tiene la forma de una onda plana uniforme, como se muestra en la Figura\(\PageIndex{2}\). El campo eléctrico se orienta en la dirección perpendicular a las placas, y el campo magnético se orienta en la dirección paralela a las placas. La dirección de propagación\({\bf E}\times{\bf H}\) para el\(_0\) modo TM siempre apunta en la misma dirección; es decir, a lo largo del eje de la línea de transmisión. Por lo tanto, las líneas microstrip presentan nominalmente una estructura de campo electromagnético transversal (TEM).
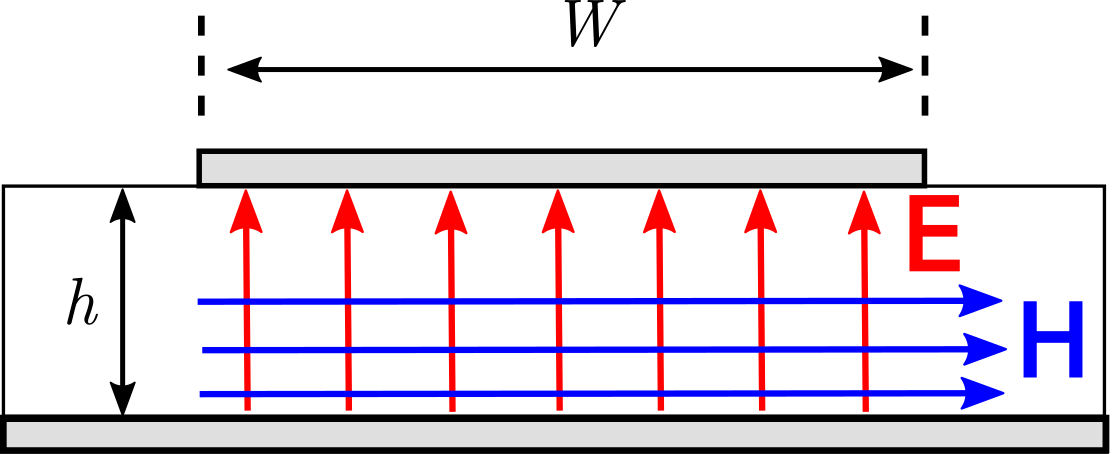
El ancho limitado\(W\) de la traza da como resultado un “campo de franjas”, es decir, desviaciones significativas de la estructura del\(_0\) campo TM en el dieléctrico más allá de los bordes de la traza y por encima de la traza. Los campos marginales pueden desempeñar un papel importante en la determinación de la impedancia característica\(Z_0\). Dado que\(Z_0\) es un parámetro importante en el análisis y diseño de sistemas que utilizan líneas de transmisión, estamos motivados no solo\(Z_0\) para determinar para la línea de microcinta, sino también para comprender cómo la variación en los\(W\) efectos\(Z_0\). Abordemos este tema considerando los siguientes tres casos especiales, en orden:
- \(W \gg h\), al que nos referiremos como el caso “amplio”.
- \(W \ll h\), al que nos referiremos como el caso “estrecho”.
- \(W \sim h\); es decir, el caso intermedio en el cual\(h\) e\(W\) igual a dentro de un orden de magnitud más o menos.
Estuche ancho
Si\(W \gg h\), la mayor parte de la energía asociada con la propagación de las ondas se encuentra directamente debajo de la traza, y la Figura\(\PageIndex{2}\) proporciona una impresión relativamente precisa de los campos en esta región. “La impedancia característica se\(Z_0\) puede determinar usando el modelo de línea de transmisión “" elemento agrupado "” usando la siguiente expresión:”
\[Z_0 = \sqrt{\frac{R'+j\omega L'}{G'+j\omega C'}} \nonumber \]
donde\(R'\),\(G'\)\(C'\), y\(L'\) son la resistencia, conductancia, capacitancia e inductancia por unidad de longitud, respectivamente. Para el presente análisis, nada se pierde asumiendo que la pérdida es insignificante; por lo tanto, supongamos\(R' \ll \omega L'\) y\(G' \ll \omega G'\), cediendo
\[Z_0 \approx \sqrt{\frac{L'}{C'}} \nonumber \]
Por lo tanto, el problema se reduce a determinar la capacitancia y la inductancia de la línea de transmisión.
La línea de microcinta ancha se asemeja a un condensador de placa paralela cuya separación entre placas\(d\) es muy pequeña en comparación con el área de la placa\(A\). En este caso, los campos de franjas pueden considerarse insignificantes y se encuentra que la capacitancia\(C\) viene dada por
\[C \approx \frac{\epsilon A}{d} ~~~ \mbox{(parallel plate capacitor)} \nonumber \]
En términos de línea de microcinta ancha,\(A=Wl\) donde\(l\) es la longitud, y\(d=h\). Por lo tanto:
\[C' \triangleq \frac{C}{l} \approx \frac{\epsilon W}{h} ~~~ (W \gg h) \nonumber \]
Para determinar\(L'\), considere la vista de la línea de microcinta que se muestra en la Figura\(\PageIndex{3}\).
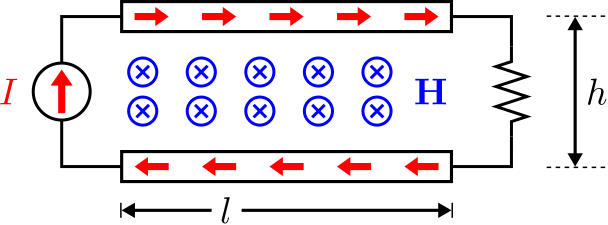
Aquí una fuente de corriente aplica una corriente constante a\(I\) la izquierda, y una carga resistiva cierra el bucle de corriente a la derecha. La ley de Ampere para magnetostáticos y la “regla de la mano derecha” asociada requieren que\({\bf H}\) se dirija a la página y sea aproximadamente uniforme. El flujo magnético entre la traza y el plano de tierra es
\[\Phi = \int_{\mathcal{S}} { {\bf B}\cdot d{\bf s} } \nonumber \]
donde\({\mathcal S}\) está la superficie delimitada por el bucle de corriente y\({\bf B}=\mu_0{\bf H}\). En el presente problema, el área de\({\mathcal S}\) es\(hl\) y\({\bf H}\) es aproximadamente constante sobre\({\mathcal S}\), por lo que:
\[\Phi \approx \mu_0 H hl \nonumber \]
donde\(H\) esta la magnitud de\({\bf H}\). A continuación, recordemos que:
\[L \triangleq \frac{\Phi}{I} \label{m0186_eL} \]
Entonces, podemos determinar\(L\) si somos capaces de obtener una expresión para\(I\) en términos de\(H\). Esto se puede hacer de la siguiente manera. Primero, tenga en cuenta que podemos expresar\(I\) en términos de la densidad de corriente en la traza; es decir,
\[I = J_s W \nonumber \]
donde\(J_s\) está la densidad de corriente (unidades base SI de A/m) en la traza. A continuación, observamos que la condición de límite para\({\bf H}\) en la traza requiere que la discontinuidad en la componente tangente de\({\bf H}\) ir de la traza (donde está la intensidad del campo magnético\(H\)) a más allá de la traza (es decir, fuera de la línea de transmisión, donde la intensidad del campo magnético es aproximadamente cero) sea igual a la corriente superficial. Así,\(J_s \approx H\) y
\[I = J_s W \approx H W \nonumber \]
Volviendo a la Ecuación\ ref {M0186_EL}, encontramos:
\[L \triangleq \frac{\Phi}{I} \approx \frac{\mu_0 H hl}{HW} = \frac{\mu_0 hl}{W} \nonumber \]
Posteriormente,
\[L' \triangleq \frac{L}{l} \approx \frac{\mu_0 h}{W} ~~~ (W \gg h) \nonumber \]
Ahora se encuentra que la impedancia característica es
\[Z_0 \approx \sqrt{\frac{L'}{C'}} \approx \sqrt{\frac{\mu_0 h/W}{\epsilon W/h}} = \sqrt{\frac{\mu_0}{\epsilon}}\frac{h}{W} \nonumber \]
El factor\(\sqrt{\mu_0/\epsilon}\) es reconocido como la impedancia de onda\(\eta\). Es conveniente expresar esto en términos de la impedancia de onda espacial libre\(\eta_0\triangleq\sqrt{\mu_0/\epsilon_0}\), conduciendo a la expresión que buscamos:
\[\boxed{ Z_0 \approx \frac{\eta_0}{\sqrt{\epsilon_r}}\frac{h}{W} ~~~ (W \gg h) } \label{m0186_eZ0wide} \]
La impedancia característica de la línea de microcinta “wide” (\(W \gg h\)) viene dada aproximadamente por la Ecuación\ ref {M0186_EZ0wide}.
Vale la pena señalar que la impedancia característica de la línea de transmisión ancha es proporcional a\(h/W\). El factor\(h/W\) también ocupa un lugar destacado en los casos de ancho estrecho e intermedio, como veremos pronto.
Estuche estrecho
La figura\(\PageIndex{2}\) no representa con precisión los campos en el caso de que\(W \ll h\). En cambio, gran parte de la energía asociada a los campos eléctrico y magnético se encuentra más allá y por encima de la huella. Aunque estos campos son relativamente complejos, podemos desarrollar un modelo rudimentario de la estructura de campo considerando las condiciones límite relevantes. En particular, el componente tangencial de\({\bf E}\) debe ser cero en las superficies de la traza y plano de tierra. Además, esperamos que las líneas de campo magnético sean perpendiculares a las líneas de campo eléctrico para que la dirección de propagación sea a lo largo del eje de la línea. Estos conocimientos conducen a la Figura\(\PageIndex{4}\).
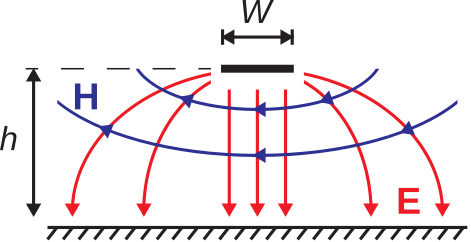
Tenga en cuenta que las líneas de campo que se muestran en la Figura\(\PageIndex{4}\) son bastante similares a las de la línea de cable paralelo (Sección 7.1). Si elegimos diámetro\(d=W\) y espaciado de cables\(D=2h\), entonces los campos de la línea de microcinta en el espaciador dieléctrico deben ser similares a los de la línea de cable paralela entre las líneas. Esto se muestra en la Figura\(\PageIndex{5}\). Obsérvese que los campos por encima del espaciador dieléctrico en la línea de microcinta normalmente serán algo diferentes (ya que el material por encima de la traza es típicamente diferente; por ejemplo, aire). No obstante, sigue siendo cierto que esperamos que la mayor parte de la energía esté contenida en el dieléctrico, por lo que asumiremos que esta diferencia tiene un efecto relativamente pequeño.
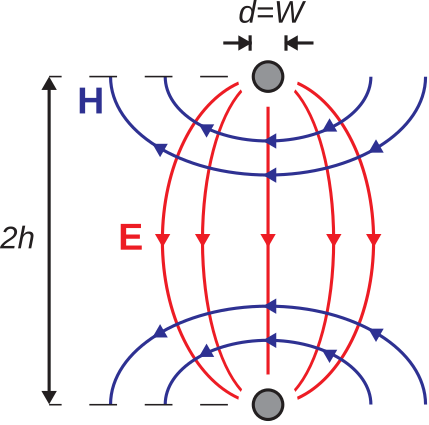
A continuación, continuamos afinando el modelo introduciendo el plano de tierra, como se muestra en la Figura\(\PageIndex{6}\): Los campos en el medio espacio superior no se perturban cuando hacemos esto, ya que los campos de la Figura\(\PageIndex{5}\) ya satisfacen las condiciones límite impuestas por el nuevo plano de tierra. Así, vemos que la línea de transmisión por cable paralelo proporciona una guía bastante buena para la estructura de los campos para la línea de transmisión estrecha, al menos en la región dieléctrica del medio espacio superior.
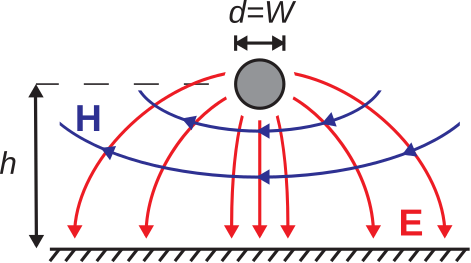
Ahora estamos listos para estimar la impedancia característica de la línea\(Z_0\approx\sqrt{L'/C'}\) de microcinta estrecha de baja pérdida. Despreciando las diferencias señaladas anteriormente, estimamos que esto es aproximadamente igual a la impedancia característica de la línea de alambre paralela análoga (\(d=W\)y\(D=2h\)). Bajo este supuesto, obtenemos de la Ecuación 7.1.8:
\[\boxed{ Z_0 \sim \frac{1}{\pi}\frac{\eta_0}{\sqrt{\epsilon_r}}\ln\left( 4h/W \right) ~~~ (W \ll h) } \label{m0186_eZ0narrow} \]
Esta estimación exhibirá solo precisión de “orden de magnitud” (de ahí el símbolo “\(\sim\)”), ya que se ignora la contribución de los campos en la mitad del espacio relevante. Sin embargo, esperamos que la Ecuación\ ref {M0186_EZ0Narrow} capture con precisión la\(Z_0\) dependencia de los parámetros\(\epsilon_r\) y\(h/W\). Estas propiedades pueden ser útiles para realizar ajustes finos en un diseño de microcinta.
La impedancia característica de la línea de microcinta “estrecha” (\(W \ll h\)) se puede aproximar aproximadamente mediante la Ecuación\ ref {M0186_EZ0Narrow}.
Caso intermedio
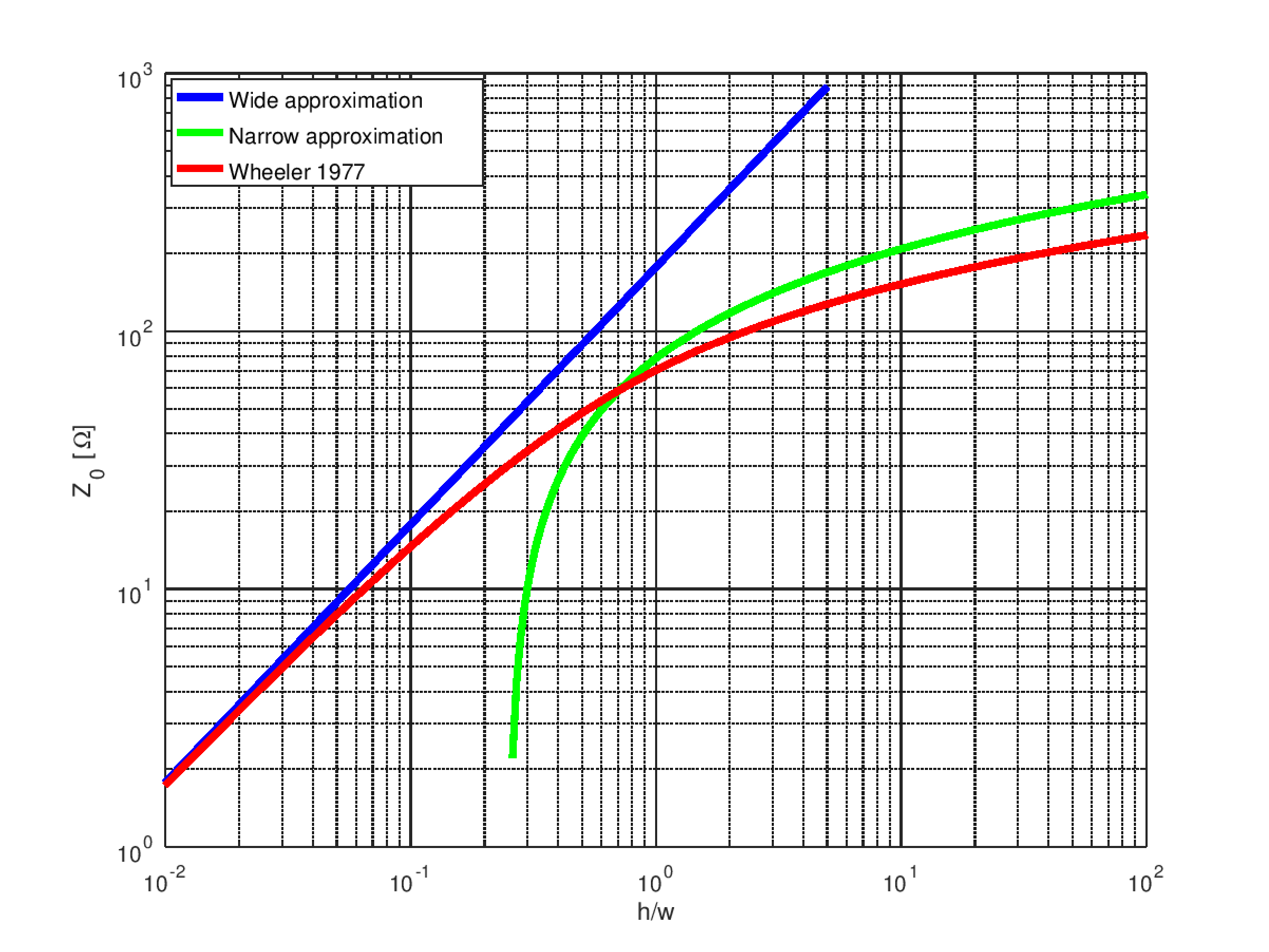
Una expresión para\(Z_0\) en el caso intermedio —incluso una estimación aproximada— es difícil de derivar, y más allá del alcance de este libro. Sin embargo, no estamos completamente en la oscuridad, ya que podemos anticipar razonablemente que\(Z_0\) en el caso intermedio debe ser intermedio a las estimaciones proporcionadas por los casos amplios y estrechos. Esto se demuestra mejor con el ejemplo. La figura\(\PageIndex{7}\) muestra estimaciones del\(Z_0\) uso de las expresiones ancha y estrecha (curvas azules y verdes, respectivamente) para una implementación particular de la línea de microcinta (ver Ejemplo\(\PageIndex{1}\) para más detalles).
Dado que\(Z_0\) varía sin problemas con\(h/W\), es razonable esperar que simplemente promediar los valores generados utilizando los supuestos amplios y estrechos daría una estimación bastante buena cuándo\(h/W\sim 1\).
Sin embargo, también es posible obtener una estimación precisa directamente. Una fórmula ampliamente aceptada y ampliamente aplicable se proporciona en Wheeler 1977 (citada en “Lectura adicional” al final de esta sección). Esta expresión es válida en todo el rango de\(h/W\), no meramente en el caso intermedio de\(h/W\sim 1\). Aquí está:
\[Z_0 \approx \frac{42.4~\Omega}{\sqrt{\epsilon_r+1}} ~\times \ln\left[ 1 + \frac{4h}{W'} \left( K + \sqrt{ K^2 + \frac{1+1/\epsilon_r}{2}\pi^2 } \right) \right] \label{m0186_eWheeler10} \]
donde
\[K \triangleq \frac{ 14 + 8/\epsilon_r }{ 11 } \left( \frac{4h}{W'} \right) \nonumber \]
y\(W'\) se\(W\) ajusta para tener en cuenta el grosor\(t\) de la línea de microcinta. Típicamente\(t\ll W\) y\(t \ll h\), para lo cual\(W'\approx W\). Aunque complicada, esta fórmula no debería ser del todo sorprendente. Por ejemplo, anotar los parámetros\(h\) y\(W\) aparecer en esta fórmula como el factor\(4h/W\), que encontramos en la aproximación “estrecha”. También, vemos que la fórmula indica\(Z_0\) incrementos con incremento\(h/W\) y decreciente\(\epsilon_r\), como determinamos tanto en los casos “estrechos” como en los “anchos”.
El siguiente ejemplo proporciona una demostración para el caso muy común de implementación de microcinta en material de placa de circuito FR4.
Las placas de circuito impreso FR4 consisten en un sustrato que tiene\(h\cong 1.575\) mm y\(\epsilon_r\approx 4.5\). La figura\(\PageIndex{7}\) muestra\(Z_0\) en función de\(h/W\), según lo determinado por las aproximaciones anchas y estrechas, junto con el valor obtenido con la fórmula Wheeler 1977. El lado izquierdo de la parcela representa la condición ancha, mientras que el lado derecho de esta parcela representa la condición estrecha. La fórmula Wheeler 1977 es una estimación precisa sobre todo el lapso horizontal. Tenga en cuenta que la aproximación amplia es precisa solo para más\(h/W<0.1\) o menos, mejorando con la disminución\(h/W\) como se esperaba. La aproximación estrecha sobreestima\(Z_0\) por un factor de aproximadamente 1.4 (es decir, aproximadamente 40%). Esto es consistente con nuestra observación anterior de que esta aproximación debería arrojar solo una precisión de “orden de magnitud”. Sin embargo, la aproximación estrecha exhibe aproximadamente la misma tasa de\(h/W\) aumento que la fórmula Wheeler 1977.
También vale la pena señalar de Figura\(\PageIndex{7}\) el resultado importante y de uso común para\(Z_0\approx 50~\Omega\) el que se obtiene\(h/W\approx 0.5\). Así, una línea de\(50~\Omega\) microcinta en FR4 tiene un ancho de traza de aproximadamente 3 mm.
Un útil “quitar” de este ejemplo es que las aproximaciones amplias y estrechas sirven como guías útiles para entender cómo\(Z_0\) cambia en función de\(h/W\) y\(\epsilon_r\). Esto es útil especialmente para realizar ajustes en el diseño de una línea de microcinta una vez que\(Z_0\) se obtiene un valor preciso de de algún otro método; por ejemplo, usando la fórmula Wheeler 1977 o a partir de mediciones.
La construcción de la placa de circuito FR4 es tan común que merece destacarse el resultado del ejemplo anterior:
En la construcción de placa de circuito impreso FR4 (espesor del sustrato\(1.575\) mm, permitividad relativa\(\approx 4.5\), espesor de traza insignificante),\(Z_0\approx 50~\Omega\) requiere un ancho de traza de aproximadamente 3 mm. \(Z_0\)escala aproximadamente en proporción a\(h/W\) alrededor de este valor.
Las aproximaciones más simples para también\(Z_0\) se emplean comúnmente en el diseño y análisis de líneas de microcinta. Estas expresiones están limitadas en el rango\(h/W\) para el que son válidas, y generalmente pueden mostrarse como casos especiales o aproximaciones de la Ecuación\ ref {M0186_Ewheeler10}. Sin embargo, a veces son útiles para cálculos rápidos de “reverso del sobre”.
Longitud de onda en línea microstrip
Una fórmula general precisa para la longitud de onda\(\lambda\) en la línea de microcinta es igualmente difícil de derivar. Una técnica aproximada útil emplea un resultado de la teoría de ondas planas uniformes en medios no acotados. Para tales ondas, la constante de propagación de fase\(\beta\) viene dada por
\[\beta = \omega\sqrt{\mu\epsilon} \nonumber \]
Resulta que la estructura del campo electromagnético para la onda guiada en una línea de microcinta es similar en el sentido de que exhibe una estructura de campo TEM, al igual que la onda plana uniforme. Sin embargo, la onda guiada es diferente en que existe tanto en el separador dieléctrico como en el aire por encima del espaciador. Así, presumimos que\(\beta\) para la onda guiada puede aproximarse como la de una onda plana uniforme en medios no acotados que tengan la misma permeabilidad\(\mu_0\) pero una permitividad relativa diferente, a la que asignaremos el símbolo\(\epsilon_{r,eff}\) (para “permitividad relativa efectiva”). Entonces:
\[\begin{aligned} \beta &\approx \omega\sqrt{\mu_0~\epsilon_{r,eff}~\epsilon_0} ~~~\mbox{(low-loss microstrip)} \nonumber \\ &=\beta_0 \sqrt{\epsilon_{r,eff}}\end{aligned} \nonumber \]
En otras palabras, la constante de propagación de fase en una línea de microcinta se puede aproximar como la propagación de fase en espacio libre multiplicada\(\beta_0\triangleq\omega\sqrt{\mu_0\epsilon_0}\) por un factor de corrección\(\sqrt{\epsilon_{r,eff}}\).
A continuación,\(\epsilon_{r,eff}\) se aproxima groseramente como el promedio de la permitividad relativa de la losa dieléctrica y la permitividad relativa del espacio libre; es decir:
\[\epsilon_{r,eff} \approx \frac{\epsilon_r+1}{2} \label{m0186_eeff} \]
Existen diversos refinamientos para mejorar esta aproximación; sin embargo, en la práctica, las variaciones en el valor del\(\epsilon_r\) dieléctrico debido a los procesos de fabricación típicamente hacen que una estimación más precisa sea irrelevante.
Utilizando este concepto, obtenemos
\[\lambda = \frac{2\pi}{\beta} = \frac{2\pi}{\beta_0\sqrt{\epsilon_{r,eff}}} = \frac{\lambda_0}{\sqrt{\epsilon_{r,eff}}} \nonumber \]
donde\(\lambda_0\) está la longitud de onda del espacio libre\(c/f\). De manera similar, la velocidad de fase se\(v_p\) puede estimar usando la relación
\[v_p = \frac{\omega}{\beta} = \frac{c}{\sqrt{\epsilon_{r,eff}}} \nonumber \]
es decir, la velocidad de fase en microcinta es más lenta que\(c\) por un factor de\(\sqrt{\epsilon_{r,eff}}\).
FR4 es un dieléctrico epoxi de fibra de vidrio de baja pérdida que se usa comúnmente para hacer placas de circuitos impresos (consulte “Lectura adicional” al final de esta sección). Para FR4,\(\epsilon_r\approx 4.5\). Por lo tanto, la permitividad relativa efectiva es:
\[\epsilon_{r,eff}\approx(4.5+1)/2 = 2.75 \nonumber \]
Así, estimamos que la velocidad de fase para la onda guiada por esta línea es aproximadamente\(c/\sqrt{2.75}\); es decir, 60% de\(c\). De manera similar, la longitud de onda de esta onda es aproximadamente 60% de la longitud de onda del espacio libre. En la práctica, se encuentra que estos valores son ligeramente menores; típicamente 50% — 55%. La diferencia es atribuible a la aproximación bruta de la Ecuación\ ref {m0186_eeff}.
- La referencia en “Lectura adicional” al final de esta sección puede ser útil si no está familiarizado con este concepto. ↩