9.7: Radiación de campo lejano de un dipolo de media onda
- Page ID
- 83723
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una distribución de corriente simple e importante es la del dipolo delgado de media onda (HWD), que se muestra en la Figura\(\PageIndex{1}\).
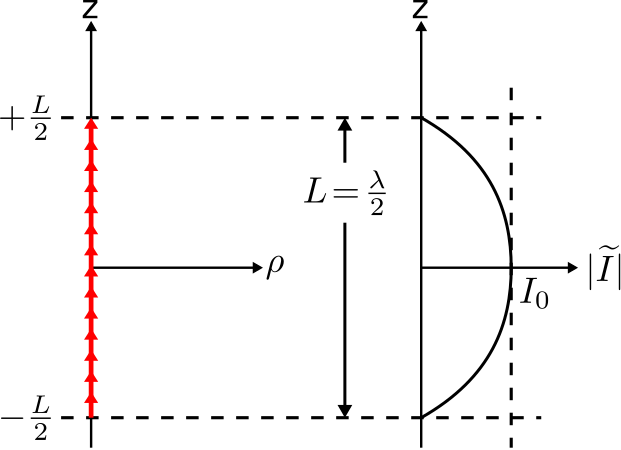
Esta es la distribución esperada en un cable recto delgado que tiene longitud\(L=\lambda/2\), donde\(\lambda\) está la longitud de onda. Esta distribución se describe matemáticamente de la siguiente manera:
\[\widetilde{I}(z) \approx I_0 \cos \left( \pi \frac{z}{L} \right) ~~~ \mbox{for} ~ \left|z\right|\le\frac{L}{2} \label{m0200_eHWD1} \]
donde\(I_0\) (SI unidades base de A) es una constante de valor complejo que indica la magnitud máxima de la corriente y su fase. Tenga en cuenta que la corriente es cero en los extremos del dipolo; es decir,\(\widetilde{I}(z) = 0\) para\(\left|z\right|= L/2\). Obsérvese también que esta distribución de “pulso coseno” es muy similar a la distribución triangular de la ESD, y recuerda a la variación sinusoidal de la corriente en una onda estacionaria.
Dado que\(L=\lambda/2\) para el HWD, la Ecuación\ ref {M0200_EHWD1} puede escribirse de manera equivalente:
\[\widetilde{I}(z) \approx I_0 \cos \left( 2\pi \frac{z}{\lambda} \right) \label{m0200_eHWD2} \]
El campo electromagnético irradiado por esta distribución de corriente podrá calcularse utilizando el método descrito en la Sección 9.6, en particular:
\[ \tilde{\mathbf{E}}(\mathbf{r}) \approx \hat{\theta} j \frac{\eta}{2} \frac{e^{-j \beta r}}{r}(\sin \theta) \cdot \left[ \frac{1}{\lambda} \int_{-L / 2}^{+L / 2} \tilde{I}\left(z^{\prime}\right) e^{+j \beta z^{\prime} \cos \theta} d z^{\prime}\right] \label{m0200_eESDE} \]
que es válido para puntos de campo\({\bf r}\) alejados del dipolo; es decir, para\(r\gg L\) y\(r\gg \lambda\). Para el HWD, la cantidad entre corchetes es
\[\frac{I_0}{\lambda}\int_{-\lambda/4}^{+\lambda/4} \cos \left( 2\pi \frac{z'}{\lambda} \right) e^{+j\beta z'\cos{\theta}} dz' \nonumber \]
La evaluación de esta integral es sencilla, pero tediosa. La integral reduce a
\[\frac{I_0}{\pi} \frac{\cos\left[\left(\pi/2\right)\cos\theta\right]}{\sin^2\theta} \nonumber \]
Sustitución en Ecuación\ ref {M0200_EESDE} rendimientos
\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \frac{\eta I_0}{2\pi} \frac{\cos\left[\left(\pi/2\right)\cos\theta\right]}{\sin\theta} \frac{e^{-j\beta r}}{r} \nonumber \]
El campo magnético se puede determinar a partir de este resultado utilizando la ley de Ampere. Sin embargo, un método más sencillo es utilizar el hecho de que el campo eléctrico, el campo magnético y la dirección de propagación\(\hat{\bf r}\) son mutuamente perpendiculares y están relacionados por:
\[\widetilde{\bf H} = \frac{1}{\eta} \hat{\bf r} \times \widetilde{\bf E} \nonumber \]
Esta relación indica que el campo magnético será\(+\hat{\bf \phi}\) -dirigido.
La magnitud y polarización del campo radiado es similar a la del dipolo eléctrico corto (ESD; Sección 9.5). En la Figura se muestra una comparación de las magnitudes en cualquier plano radial que contenga el\(z\) eje\(\PageIndex{2}\).
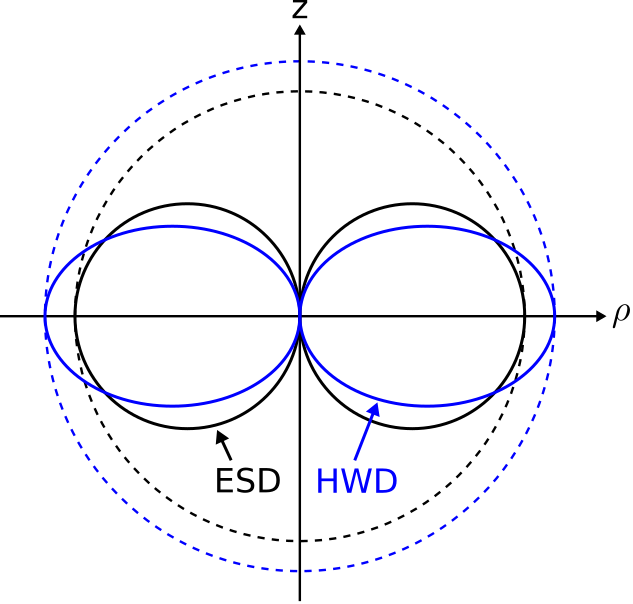
Para cualquiera de las dos distribuciones de corriente, la magnitud máxima de los campos ocurre en el\(z=0\) plano. Para una corriente terminal dada\(I_0\), la magnitud máxima es mayor para el HWD que para el ESD. Ambas distribuciones de corriente producen magnitud cero a lo largo del eje del dipolo. Las características de polarización de los campos de ambas distribuciones de corriente son idénticas.
Lectura adicional:
- “Antena dipolo” (sección titulada “Dipolo de media onda”) en Wikipedia.


