6.2: Serie de Fourier de Tiempo Continuo (CTFS)
- Page ID
- 86554
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
En este módulo, derivaremos una expansión para funciones periódicas de tiempo continuo y, al hacerlo, derivaremos la Serie de Fourier de Tiempo Continuo (CTFS).
Dado que los exponenciales complejos (Sección 1.8) son funciones propias de sistemas lineales invariables en el tiempo (LTI) (Sección 14.5), calcular la salida de un sistema LTI\(\mathscr{H}\) dado\(e^{st}\) como entrada equivale a multiplicación simple, donde\(H(s) \in \mathbb{C}\) corresponde el valor propio\(s\). Como se muestra en la figura, una entrada exponencial simple produciría la salida
\[y(t)=H(s) e^{s t} \nonumber \]
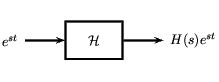
Usando esto y el hecho de que\(\mathscr{H}\) es lineal, calcular\(y(t)\) para combinaciones de exponenciales complejos también es sencillo.
\[\begin{align} c_{1} e^{s_{1} t}+c_{2} e^{s_{2} t} &\rightarrow c_{1} H\left(s_{1}\right) e^{s_{1} t}+c_{2} H\left(s_{2}\right) e^{s_{2} t} \\[4pt] \sum_{n} c_{n} e^{s_{n} t} &\rightarrow \sum_{n} c_{n} H\left(s_{n}\right) e^{s_{n} t} \end{align} \nonumber \]
La acción de\(H\) sobre una entrada como las de las dos ecuaciones anteriores es fácil de explicar. \(\mathbf{\mathscr{H}}\)escala independientemente cada componente exponencial\(e^{s_nt}\) por un número complejo diferente\(H\left(s_{n}\right) \in \mathbb{C}\). Como tal, si podemos escribir una función\(f(t)\) como una combinación de exponenciales complejos nos permite calcular fácilmente la salida de un sistema.
Síntesis de la serie de Fourier
Joseph Fourier demostró que una arbitraria\(f(t)\) puede escribirse como una combinación lineal de sinusoides complejos armónicos
\[f(t)=\sum_{n=-\infty}^{\infty} c_{n} e^{j \omega_{0} n t} \label{6.3} \]
donde\(\omega_0=\frac{2 \pi}{T}\) está la frecuencia fundamental. Para casi todos\(f(t)\) los intereses prácticos, existe\(c_n\) para hacer verdadera la Ecuación\ ref {6.3}. Si\(f(t)\) es energía finita\(\left(f(t) \in L^{2}[0, T]\right)\), entonces la igualdad en la Ecuación\ ref {6.3} se mantiene en el sentido de convergencia de energía; si\(f(t)\) es continua, entonces la Ecuación\ ref {6.3} se mantiene puntual. Además, si\(f(t)\) cumple algunas condiciones suaves (las condiciones de Dirichlet), entonces la Ecuación\ ref {6.3} se mantiene puntual en todas partes excepto en los puntos de discontinuidad.
Los\(c_n\) -llamados coeficientes de Fourier- nos dicen “cuánto” de la sinusoide\(e^{j \omega_0 nt}\) está en\(f(t)\). La fórmula\(f(t)\) se muestra como una suma de exponenciales complejos, cada uno de los cuales es fácilmente procesado por un sistema LTI (ya que es una función propia de cada sistema LTI). Matemáticamente, nos dice que el conjunto de exponenciales complejos\(\left\{\forall n, n \in \mathbb{Z}:\left(e^{j \omega_{0} n t}\right)\right\}\) forman una base para el espacio de funciones de tiempo continuo\(T\) -periódicas.
Ejemplo\(\PageIndex{1}\)
Eso lo sabemos por la fórmula de Euler\(\cos (\omega t)+\sin (\omega t)=\frac{1-j}{2} e^{j \omega t}+\frac{1+j}{2} e^{-j \omega t}\).
Demostración de Síntesis con Sinusoides
Análisis de la serie de Fourier
Encontrar los coeficientes de expansión de la serie de Fourier implica alguna manipulación algebraica de la fórmula de síntesis. En primer lugar vamos a multiplicar ambos lados de la ecuación por\(e^{-\left(j \omega_{0} k t\right)}\), donde\(k \in \mathbb{Z}\).
\[f(t) e^{-\left(j \omega_{0} k t\right)}=\sum_{n=-\infty}^{\infty} c_{n} e^{j \omega_{0} n t} e^{-\left(j \omega_{0} k t\right)} \label{6.4} \]
Ahora integren ambas partes en un periodo determinado,\(T\):
\[\int_{0}^{T} f(t) e^{-\left(j \omega_{0} k t\right)} \mathrm{d} t=\int_{0}^{T} \sum_{n=-\infty}^{\infty} c_{n} e^{j \omega_{0} n t} e^{-\left(j \omega_{0} k t\right)} \mathrm{d} t \label{6.5} \]
En el lado derecho podemos cambiar la suma e integral y factorizar la constante fuera de la integral.
\[\int_{0}^{T} f(t) e^{-\left(j \omega_{0} k t\right)} \mathrm{d} t=\sum_{n=-\infty}^{\infty} c_{n} \int_{0}^{T} e^{j \omega_{0}(n-k) t} \mathrm{d} t \label{6.6} \]
Ahora que hemos hecho esto aparentemente más complicado, centrémonos solo en la integral,\(\int_{0}^{T} e^{j \omega_{0}(n-k) t} \mathrm{d} t\), en el lado derecho de la ecuación anterior. Para esta integral tendremos que considerar dos casos:\(n=k\) y\(n \neq k\). Para\(n=k\) contaremos con:
\[\forall n, n=k:\left(\int_{0}^{T} e^{j \omega_{0}(n-k) t} \mathrm{d} t=T\right) \label{6.7} \]
Para\(n \neq k\), contaremos con:
\[\forall n, n \neq k:\left(\int_{0}^{T} e^{j \omega_{0}(n-k) t} \mathrm{d} t=\int_{0}^{T} \cos \left(\omega_{0}(n-k) t\right) \mathrm{d} t+j \int_{0}^{T} \sin \left(\omega_{0}(n-k) t\right) \mathrm{d} t\right) \label{6.8} \]
Pero\(\cos(\omega_0(n−k)t)\) tiene un número entero de periodos,\(n−k\), entre 0 y\(T\). Imagina una gráfica del coseno; debido a que tiene un número entero de periodos, hay áreas iguales por encima y por debajo del eje x de la gráfica. Esta afirmación también es cierta para\(\sin(\omega_0(n−k)t)\). Lo que esto significa es
\[\int_{0}^{T} \cos \left(\omega_{0}(n-k) t\right) \mathrm{d} t=0 \nonumber \]
que también se sostiene para la integral que implica la función sinusoidal. Por lo tanto, concluimos lo siguiente sobre nuestra integral de interés:
\ [\ int_ {0} ^ {T} e^ {j\ omega_ {0} (n-k) t}\ mathrm {d} t=\ left\ {\ begin {array} {l}
T\ text {if} n=k\\
0\ text {de lo contrario}
\ end {array}\ right. \ nonumber\]
Ahora volvamos nuestra atención a nuestra complicada ecuación, Ecuación\ ref {6.6}, para ver si podemos terminar de encontrar una ecuación para nuestros coeficientes de Fourier. Usando los hechos que acabamos de probar anteriormente, podemos ver que la única ecuación de tiempo\ ref {6.6} tendrá un resultado distinto de cero es cuando\(k\) y\(n\) son iguales:
\[\forall n, n=k:\left(\int_{0}^{T} f(t) e^{-\left(j \omega_{0} n t\right)} \mathrm{d} t=T c_{n}\right) \nonumber \]
Finalmente, tenemos nuestra ecuación general para los coeficientes de Fourier:
\[c_{n}=\frac{1}{T} \int_{0}^{T} f(t) e^{-\left(j \omega_{0} n t\right)} \mathrm{d} t \nonumber \]
Ejemplo\(\PageIndex{2}\)
Considere la función de onda cuadrada dada por
\ [x (t) =\ left\ {\ begin {array} {cc}
1/2 & t\ leq 1/2\\
-1/2 & t>1/2
\ end {array}\ right. \ nonumber\]
en el intervalo de la unidad\(t \in \mathbb{Z}[0,1)\).
\ [\ begin {align*}
c_ {k} &=\ int_ {0} ^ {1} x (t) e^ {-j 2\ pi k t} d t\ nonumber\\
&=\ int_ {0} ^ {1/2}\ frac {1} {2} e^ {-j 2\ pi k t} d t-\ int_ {1/2} {1}\ frac {1} {2} e^ {-j 2\ pi k t} d t\ nonúmero\\
&=\ frac {j\ izquierda (-1+e^ {j\ pi k}\ derecha)} {2\ pi k}
\ final {alinear*}\ nonumber\]
Así, los coeficientes de Fourier de esta función encontrados usando la fórmula de análisis de series de Fourier son
\ [c_ {k} =\ left\ {\ begin {array} {cc}
-j/\ pi k &\ text {k impar}\\
0 &\ text {k par}
\ end {array}\ right. \ nonumber\]
Resumen de la serie de Fourier
Debido a que los exponenciales complejos son funciones propias de los sistemas LTI, a menudo es útil representar señales usando un conjunto de exponenciales complejos como base. La fórmula de síntesis de series de Fourier de tiempo continuo expresa una función periódica de tiempo continuo como la suma del tiempo continuo, exponenciales complejos de frecuencia discreta.
\[f(t)=\sum_{n=-\infty}^{\infty} c_{n} e^{j \omega_{0} n t} \nonumber \]
La fórmula de análisis de series de tiempo continuo de Fourier da los coeficientes de expansión de la serie de Fourier.
\[c_{n}=\frac{1}{T} \int_{0}^{T} f(t) e^{-\left(j \omega_{0} n t\right)} \mathrm{d} t \nonumber \]
En ambas ecuaciones\(\omega_0 = \frac{2 \pi}{T}\) se encuentra la frecuencia fundamental.


