15.1: Campos y números complejos
- Page ID
- 86589
Campos
Para discutir profamente el concepto de espacios vectoriales en álgebra lineal, es necesario desarrollar la noción de un conjunto de “escalares” por los cuales permitimos que se multiplique un vector. Un marco dentro del cual encajaría nuestro concepto de números reales es deseable. Así, nos gustaría un conjunto con dos operaciones asociativas, conmutativas (como suma y multiplicación estándar) y una noción de sus operaciones inversas (como resta y división). El constructo matemático algebraico que aborda esta idea es el campo. Un campo (\(S,+,*\)) es un conjunto\(S\) junto con dos operaciones binarias\(+\) y\(*\) tal que se satisfacen las siguientes propiedades.
- Cierre de S bajo\(+\): Por cada\(x\),\(y \in S\),\(x+y \in S\).
- Asociatividad de S bajo\(+\): Para cada\(x,y,z \in S\),\((x+y)+z=x+(y+z)\).
- Existencia de elemento de\(+\) identidad: Hay\(e_+ \in S\) tal que para cada\(x \in S\),\(e_+ + x = x+e_+=x\).
- Existencia de elementos\(+\) inversos: Para cada uno\(x \in S\) hay\(y \in S\) tal que\(x+y=y+x=e_+\).
- Conmutatividad de S bajo\(+\): Para cada\(x,y \in S\),\(x+y=y+x\).
- Cierre de S bajo\(*\): Por cada\(x,y \in S\),\(x*y \in S\).
- Asociatividad de S bajo\(*\): Para cada\(x,y,z \in S\),\((x*y)*z=x*(y*z)\).
- Existencia de elemento de\(*\) identidad: Hay\(e_* \in S\) tal que para cada\(x \in S\),\(e_*+x=x+e_*=x\).
- Existencia de elementos\(*\) inversos: Para cada uno\(x \in S\) con\(x \neq e_{+}\) hay\(y \in S\) tal que\(x*y=y*x=e_*\).
- Conmutatividad de S bajo\(*\): Para cada\(x,y \in S\),\(x*y=y*x\).
- Distributividad de\(*\) más\(+\): Para cada\(x,y,z \in S\),\(x*(y+z)=xy+xz\).
Si bien esta definición es bastante general, los dos campos utilizados con mayor frecuencia en el procesamiento de señales, al menos dentro del alcance de este curso, son los números reales y los números complejos, cada uno con sus operaciones típicas de suma y multiplicación.
El campo complejo
El lector, sin duda, ya está suficientemente familiarizado con los números reales con las operaciones típicas de suma y multiplicación. Sin embargo, el campo de números complejos con las operaciones típicas de adición y multiplicación puede ser desconocido para algunos. Por esa razón y su importancia para el procesamiento de señales, merece aquí una breve explicación.
Definiciones
La noción de raíz cuadrada de\(-1\) se originó con la fórmula cuadrática: la solución de ciertas ecuaciones cuadráticas existe matemáticamente solo si se\(\sqrt{-1}\) pudiera definir la llamada cantidad imaginaria. Euler utilizó\(i\) por primera vez para la unidad imaginaria pero esa notación no se afianzó hasta aproximadamente la época de Ampère. Ampère utilizó el símbolo\(i\) para denotar corriente (intensité de current). No fue sino hasta el siglo XX cuando se hizo evidente la importancia de los números complejos para la teoría de circuitos. Para entonces, el uso\(i\) para corriente estaba atrincherado y los ingenieros eléctricos ahora eligen\(j\) escribir números complejos.
Un número imaginario tiene la forma\(j b=\sqrt{-b^{2}}\). Un número complejo,\(z\), consiste en el par ordenado\((a,b)\),\(a\) es el componente real y\(b\) es el componente imaginario (el\(j\) se suprime porque el componente imaginario del par está siempre en la segunda posición). El número imaginario\(jb\) es igual\((0,b)\). Tenga en cuenta que\(a\) y\(b\) son números de valor real.
La figura\(\PageIndex{1}\) muestra que podemos ubicar un número complejo en lo que llamamos el plano complejo. Aquí,\(a\), la parte real, es la\(x\) coordenada y\(b\), la parte imaginaria, es la\(y\) coordenada.
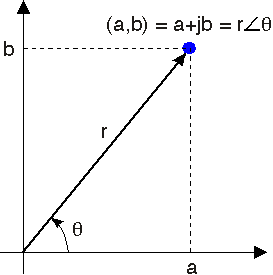
A partir de la geometría analítica, sabemos que las ubicaciones en el plano se pueden expresar como la suma de vectores, con los vectores correspondientes a las\(y\) direcciones\(x\) y. En consecuencia, un número complejo se\(z\) puede expresar como la suma (vector)\(z=a+jb\) donde\(j\) indica la\(y\) coordenada. Esta representación se conoce como la forma cartesiana de\(\mathbf{z}\). Un número imaginario no se puede agregar numéricamente a un número real; más bien, esta notación para un número complejo representa la adición de vectores, pero proporciona una notación conveniente cuando realizamos manipulaciones aritméticas.
La parte real del número complejo\(z=a+jb\), escrito como\(\operatorname{Re}(z)\), es igual\(a\). Consideramos la parte real como una función que funciona seleccionando ese componente de un número complejo no multiplicado por\(j\). La parte imaginaria de\(z\),\(\operatorname{Im}(z)\), es igual\(b\): aquella parte de un número complejo que se multiplica por\(j\). Nuevamente, tanto las partes reales como las imaginarias de un número complejo son valoradas de manera real.
El complejo conjugado de\(z\), escrito como\(z^{*}\), tiene la misma parte real que\(z\) pero una parte imaginaria del signo opuesto.
\ [\ begin {align}
z &=\ nombreoperador {Re} (z) +j\ nombreoperador {Im} (z)\ nonúmero\\
z^ {*} &=\ nombreoperador {Re} (z) -j\ nombreoperador {Im} (z)
\ end {align}\ nonumber\]
Usando la notación cartesiana, las siguientes propiedades siguen fácilmente.
- Si sumamos dos números complejos, la parte real del resultado es igual a la suma de las partes reales y la parte imaginaria es igual a la suma de las partes imaginarias. Esta propiedad se desprende de las leyes de adición de vectores.
\[a_{1}+j b_{1}+a_{2}+j b_{2}=a_{1}+a_{2}+j\left(b_{1}+b_{2}\right) \nonumber \]
De esta manera, las partes real e imaginaria permanecen separadas. - El producto de\(j\) y un número real es un número imaginario:\(ja\). El producto de\(j\) y un número imaginario es un número real:\(j(jb)=−b\) porque\(j^2=-1\). En consecuencia, multiplicar un número complejo por\(j\) gira la posición del número por\(90\) grados.
Ejercicio\(\PageIndex{1}\)
Usa la definición de suma para mostrar que las partes real e imaginaria pueden expresarse como una suma/diferencia de un número complejo y su conjugado. \(\operatorname{Re}(z)=\frac{z+z^{*}}{2}\)y\(\operatorname{Im}(z)=\frac{z-z^{*}}{2 j}\)
- Contestar
-
\(z+\bar{z}=a+j b+a-j b=2 a=2 \operatorname{Re}(z)\). Del mismo modo,\(z-\bar{z}=a+j b-(a-j b)=2 j b=2(j, \operatorname{Im}(z))\)
Los números complejos también se pueden expresar en una forma alternativa, forma polar, que encontraremos bastante útil. La forma polar surge de la interpretación geométrica de números complejos. La forma cartesiana de un número complejo se puede reescribir como
\[a+j b=\sqrt{a^{2}+b^{2}}\left(\frac{a}{\sqrt{a^{2}+b^{2}}}+j \frac{b}{\sqrt{a^{2}+b^{2}}}\right) \nonumber \]
Al formar un triángulo rectángulo que tiene lados\(a\) y\(b\), vemos que las partes real e imaginaria corresponden al coseno y al seno del ángulo base del triángulo. Obtenemos así la forma polar para números complejos.
\ [\ begin {array} {l}
z=a+j b=r\ ángulo\ theta\\
r=|z|=\ sqrt {a^ {2} +b^ {2}}\\
a=r\ cos (\ theta)\
b=r\ b=r\ sin (\ theta)
\\ theta=\ arctan\ izquierda (\ frac {b} {a} derecha)
\ end {array}\ nonumber\]
La cantidad\(r\) se conoce como la magnitud del número complejo\(z\), y frecuentemente se escribe como\(|z|\). La cantidad\(\theta\) es el ángulo del número complejo. Al usar la fórmula arco-tangente para encontrar el ángulo, debemos tomar en cuenta el cuadrante en el que se encuentra el número complejo.
Ejercicio\(\PageIndex{2}\)
Convertir\(3-2j\) a forma polar.
- Contestar
-
Para convertir\(3−2j\) a forma polar, primero ubicamos el número en el plano complejo en el cuarto cuadrante. La distancia desde el origen hasta el número complejo es la magnitud\(r\), que es igual\(\sqrt{13}=\sqrt{3^{2}+(-2)^{2}}\). El ángulo es igual\(-\arctan \left(\frac{2}{3}\right)\) o\(−0.588\) radianes (\(−33.7\)grados). La respuesta final son\(\sqrt{13} \angle (-33.7)\) grados.
Fórmula de Euler
Sorprendentemente, la forma polar de un número complejo se\(z\) puede expresar matemáticamente como
\[z = r ^{j \theta} \nonumber \]
Para mostrar este resultado, utilizamos las relaciones de Euler que expresan exponenciales con argumentos imaginarios en términos de funciones trigonométricas.
\[e^{j \theta}=\cos (\theta)+j \sin (\theta) \label{15.3} \]
\[\cos (\theta)=\frac{e^{j \theta}+e^{-(j \theta)}}{2} \label{15.4} \]
\[\sin (\theta)=\frac{e^{j \theta}-e^{-(j \theta)}}{2 j} \nonumber \]
El primero de ellos se deriva fácilmente de la serie de Taylor's para lo exponencial.
\[e^{x}=1+\frac{x}{1 !}+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\ldots \nonumber \]
Sustituyendo\(j \theta\) por\(x\), encontramos que
\[e^{j \theta}=1+j \frac{\theta}{1 !}-\frac{\theta^{2}}{2 !}-j \frac{\theta^{3}}{3 !}+\ldots \nonumber \]
porque\(j^2=-1\),\(j^3=-j\), y\(j^4=1\). Agrupar por separado los términos de valor real y los de valor imaginario,
\[e^{j \theta}=1-\frac{\theta^{2}}{2 !}+\cdots+j\left(\frac{\theta}{1 !}-\frac{\theta^{3}}{3 !}+\ldots\right) \nonumber \]
Los términos de valor real corresponden a la serie de Taylor para\(\cos(\theta)\), los imaginarios a\(\sin(\theta)\), y los resultados de la primera relación de Euler. Las relaciones restantes se derivan fácilmente de la primera. Vemos que multiplicar lo exponencial en la Ecuación\ ref {15.3} por una constante real corresponde a establecer el radio del número complejo por la constante.
Cálculo con números complejos
Sumar y restar números complejos expresados en forma cartesiana es bastante fácil: Suma (resta) las partes reales y las partes imaginarias por separado.
\[z_{1} \pm z_{2}=\left(a_{1} \pm a_{2}\right)+j\left(b_{1} \pm b_{2}\right) \nonumber \]
Multiplicar dos números complejos en forma cartesiana no es tan fácil, sino que sigue directamente de seguir las reglas habituales de la aritmética.
\ [\ begin {align}
z_ {1} z_ {2} &=\ izquierda (a_ {1} +j b_ {1}\ derecha)\ izquierda (a_ {2} +j b_ {2}\ derecha)\ nonumber\\
&=a_ {1} a_ {2} -b_ {1} b_ {2} +j\ izquierda (a_ {1} b_ {2} +a_ {2} b_ {1}\ derecha)
\ end {align}\ nonumber\]
Obsérvese que estamos, en cierto sentido, multiplicando dos vectores para obtener otro vector. La aritmética compleja proporciona una forma única de definir la multiplicación vectorial.
Ejercicio\(\PageIndex{3}\)
¿Cuál es el producto de un número complejo y su conjugado?
- Contestar
-
\(z \bar{z}=(a+j b)(a-j b)=a^{2}+b^{2}\). Por lo tanto\(z \bar{z}=r^{2}=(|z|)^{2}\).
La división requiere manipulación matemática. Convertimos el problema de división en un problema de multiplicación multiplicando tanto el numerador como el denominador por el conjugado del denominador.
\ [\ begin {align}
\ frac {z_ {1}} {z_ {2}} &=\ frac {a_ {1} +j b_ {1}} {a_ {2} +j b_ {2}}\ nonumber\\
&=\ frac {a_ {1} +j b_ {1}} {a_ {2} +j b_ {2} +j b_ {2}}}\ frac {a_ {2} -j b_ {2}} {a_ {2} -j b_ {2}}\ nonumber\\
&=\ frac {\ izquierda (a_ {1} +j b_ {1}\ derecha)\ izquierda (a_ {2} -j b_ {2}\ derecha)} {a_ {2} ^ {2} +b_ _ {2} ^ {2}} \ nonumber\\
&=\ frac {a_ {1} a_ {2} +b_ {1} b_ {2} +j\ left (a_ {2} b_ {1} -a_ {1} b_ {2}\ derecha)} {a_ {2} ^ {2} +b_ {2} ^ {2}}
\ end {align}\ nonumber\]
Debido a que el resultado final es tan complicado, es mejor recordar cómo realizar la división —multiplicando el numerador y el denominador por el complejo conjugado del denominador—que tratar de recordar el resultado final.
Las propiedades de lo exponencial hacen que calcular el producto y la relación de dos números complejos sea mucho más sencillo cuando los números se expresan en forma polar.
\ [\ begin {align}
z_ {1} z_ {2} &=r_ {1} e^ {j\ theta_ {1}} r_ {2} e^ {j\ theta_ {2}}\ nonumber\\
&=r_ {1} r_ {2} e^ {j\ left (\ theta_ {1} +\ theta_ {2}\ derecha)}
\ end {align}\ nonumber\]
\[\frac{z_{1}}{z_{2}}=\frac{r_{1} e^{j \theta_{2}}}{r_{2} e^{j \theta_{2}}}=\frac{r_{1}}{r_{2}} e^{j\left(\theta_{1}-\theta_{2}\right)} \nonumber \]
Para multiplicar, el radio es igual al producto de los radios y el ángulo a la suma de los ángulos. Para dividir, el radio es igual a la relación de los radios y el ángulo la diferencia de los ángulos. Cuando los números complejos originales están en forma cartesiana, suele valer la pena traducirlos a forma polar, luego realizar la multiplicación o división (especialmente en el caso de esta última). La suma y resta de formas polares equivale a convertir a forma cartesiana, realizar la operación aritmética y convertir de nuevo a forma polar.