2.1: Introducción a las funciones
- Page ID
- 110833
Nuestro desarrollo del concepto de función es moderno, pero bastante rápido, particularmente a la luz de que la definición actual tardó más de 300 años en llegar a su estado actual. Comenzamos con la definición de una relación.
Relaciones
Usamos la notación (2, 4) para denotar lo que se llama un par ordenado. Si piensas en las posiciones tomadas por los pares ordenados (4, 2) y (2, 4) en el plano de coordenadas (ver Figura\(\PageIndex{1}\)), entonces es inmediatamente evidente por qué el orden es importante. El par ordenado (4, 2) simplemente no es lo mismo que el par ordenado (2, 4).
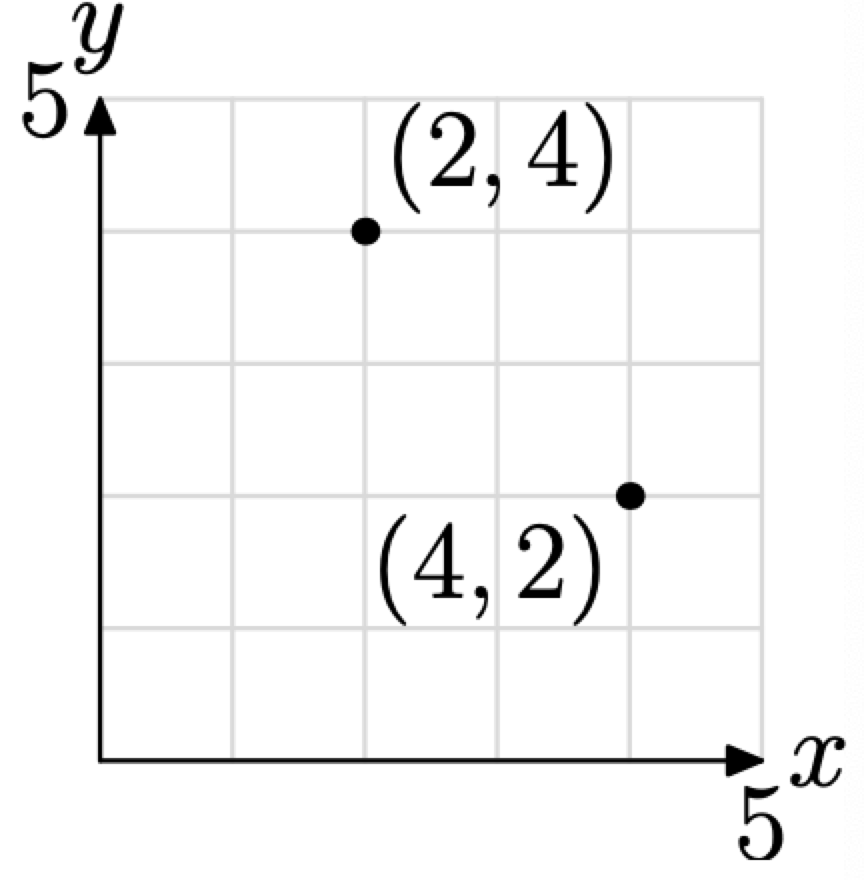
Figura\(\PageIndex{1}\)
El primer elemento de un par ordenado se llama su abscisa. El segundo elemento de un par ordenado se llama su ordenada. Así, por ejemplo, la abscisa de (4, 2) es 4, mientras que la ordenada de (4, 2) es 2.
Definición
Una colección de pares ordenados se llama relación. (2)
Por ejemplo, la colección de pares ordenados\[R=\{(0,1),(0,2),(3,4)\}\] es una relación.
Definición
El dominio de una relación es la colección de todas las abscisas de cada par ordenado.
Así, el dominio de la relación R en (2) es\[\text { Domain }=\{0,3\}\]
Tenga en cuenta que enumeramos cada abscisa solo una vez.
Definición
El rango de una relación es la colección de todas las ordenadas de cada par ordenado.
Así, el rango de la relación R en (2) es\[\text { Range }=\{1,2,4\}\]
Veamos un ejemplo.
Ejemplo\(\PageIndex{1}\)
Considerar la relación T definida por\[T=\{(1,2),(3,2),(4,5)\}\]
¿Cuál es el dominio y el alcance de esta relación?
Solución
El dominio es la colección de abscisas de cada par ordenado. De ahí que el dominio de T sea\[\text { Domain }=\{1,3,4\}\]
El rango es la colección de ordenadas de cada par ordenado. Por lo tanto, el rango de T es\[\text { Range }=\{2,5\}\]
Tenga en cuenta que enumeramos cada ordenada en el rango solo una vez.
En Ejemplo\(\PageIndex{1}\), la relación se describe listando los pares ordenados. Esta no es la única forma en que se puede describir una relación. Por ejemplo, una gráfica ciertamente representa una colección de pares ordenados.
Ejemplo\(\PageIndex{2}\)
Considera la gráfica de la relación S que se muestra en la Figura\(\PageIndex{2}\).
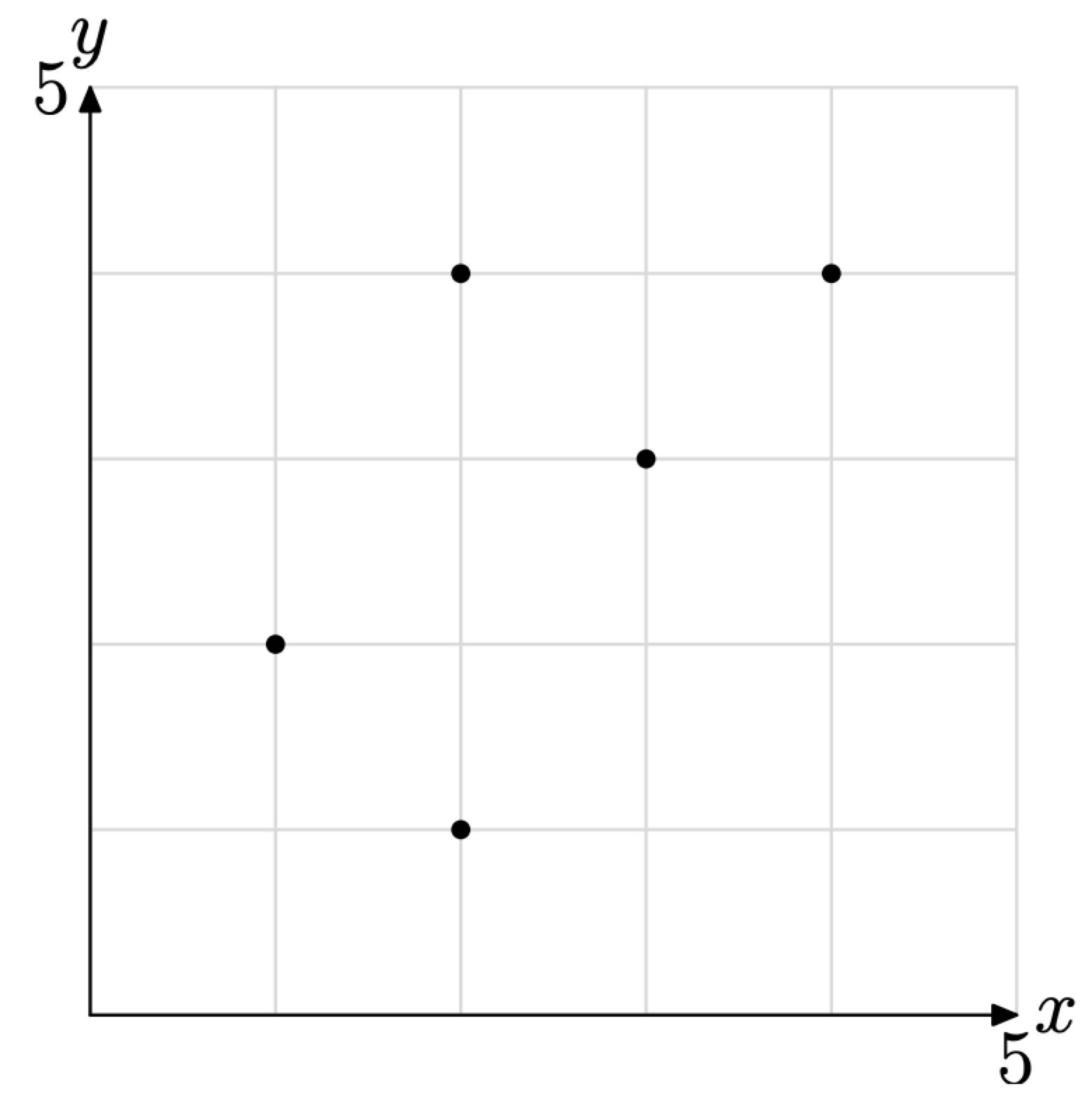
Figura\(\PageIndex{2}\) La gráfica de una relación.
¿Cuáles son el dominio y el rango de la relación S?
Solución
Hay cinco pares ordenados (puntos) trazados en la Figura\(\PageIndex{2}\). Ellos son\[S=\{(1,2),(2,1),(2,4),(3,3),(4,4)\}\]
Por lo tanto, la relación S tiene Dominio = {1, 2, 3, 4} y Rango = {1, 2, 3, 4}. En el caso del rango, observe cómo hemos ordenado las ordenadas de cada par ordenado en orden ascendente, teniendo cuidado de no enumerar ninguna ordenada más de una vez.
Funciones
Una función es un tipo de relación muy especial. Comenzamos con una definición formal.
Definición
Una relación es una función si y solo si cada objeto en su dominio está emparejado con uno y solo un objeto en su rango.
Esta no es una definición fácil, así que tomemos nuestro tiempo y consideremos algunos ejemplos. Considere, si se quiere, la relación R en (2), repetida aquí nuevamente por conveniencia.
\[R=\{(0,1),(0,2),(3,4)\}\]
El dominio es {0, 3} y el rango es {1, 2, 4}. Obsérvese que el número 0 en el dominio de R se empareja con dos números del rango, es decir, 1 y 2. Por lo tanto, R no es una función.
Hay un constructo, llamado diagrama de mapeo, que puede ser útil para determinar si una relación es una función. Para elaborar un diagrama de mapeo, primero enumere el dominio a la izquierda, luego el rango a la derecha, luego use flechas para indicar los pares ordenados en su relación, como se muestra en la Figura\(\PageIndex{3}\).
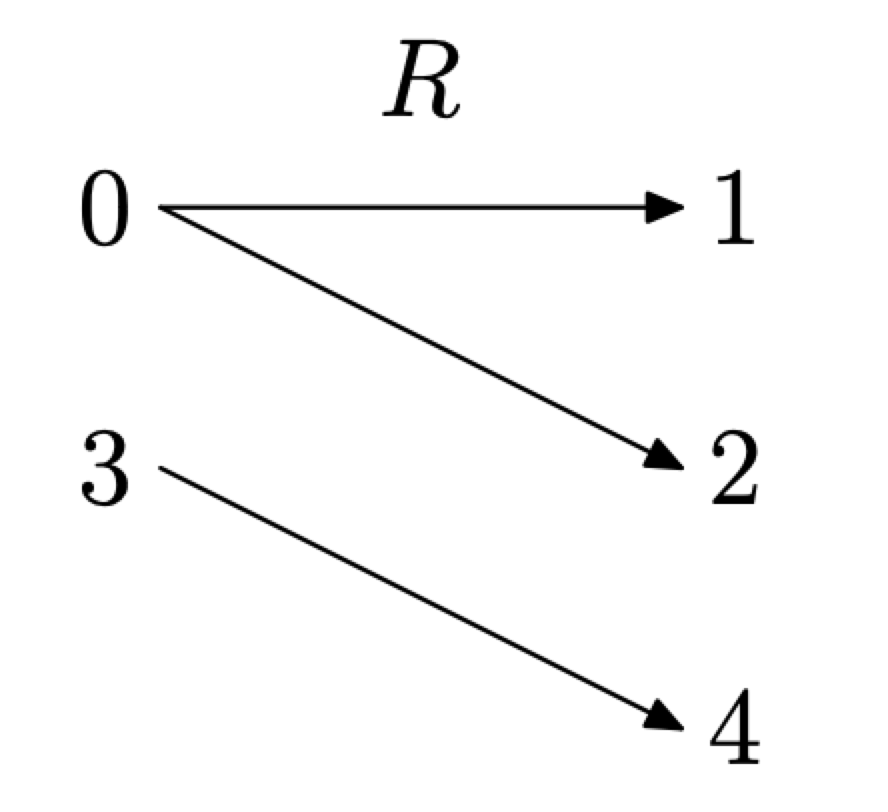
Figura\(\PageIndex{3}\) Un diagrama de mapeo para R.
Es claro a partir del diagrama de mapeo de la Figura\(\PageIndex{3}\) que el número 0 en el dominio se está emparejando (mapeando) con dos objetos de rango diferentes, a saber, 1 y 2. Así, R no es una función.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{3}\)
¿La relación descrita en Ejemplo es\(\PageIndex{1}\) una función?
Solución
Primero, vamos a repetir el listado de la relación T aquí por conveniencia.
\[T=\{(1,2),(3,2),(4,5)\}\]
A continuación, construya un diagrama de mapeo para la relación T. Enumere el dominio a la izquierda, el rango a la derecha, luego use flechas para indicar los emparejamientos, como se muestra en la Figura\(\PageIndex{4}\).
A partir del diagrama de mapeo de la Figura\(\PageIndex{4}\), podemos ver que cada objeto de dominio de la izquierda está emparejado (mapeado) con exactamente un objeto de rango a la derecha. De ahí que la relación T sea una función.
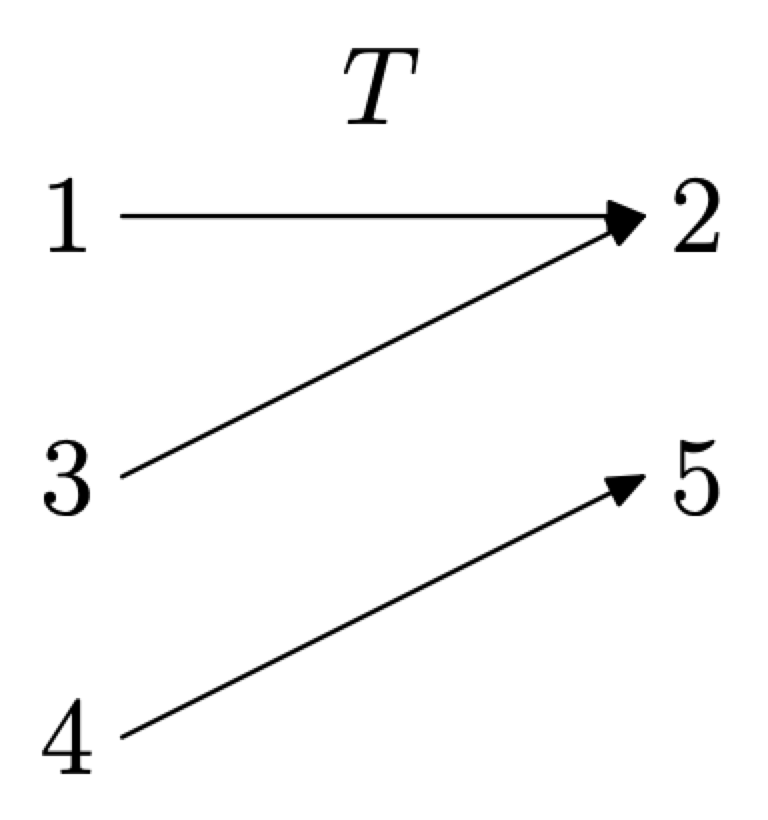
Figura\(\PageIndex{4}\). Un diagrama de mapeo para T.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{4}\)
¿La relación de Ejemplo\(\PageIndex{2}\), que se muestra en la Figura\(\PageIndex{2}\), es una función?
Solución
Primero, repetimos la gráfica de la relación de Ejemplo\(\PageIndex{2}\) aquí por conveniencia. Esto se muestra en la Figura\(\PageIndex{5}\) (a). A continuación, enumeramos los pares ordenados de la relación S.
\[S=\{(1,2),(2,1),(2,4),(3,3),(4,4)\}\]
Después creamos un diagrama de mapeo listando primero el dominio a la izquierda, el rango a la derecha, luego usando flechas para indicar los emparejamientos, como se muestra en la Figura\(\PageIndex{5}\) (b).
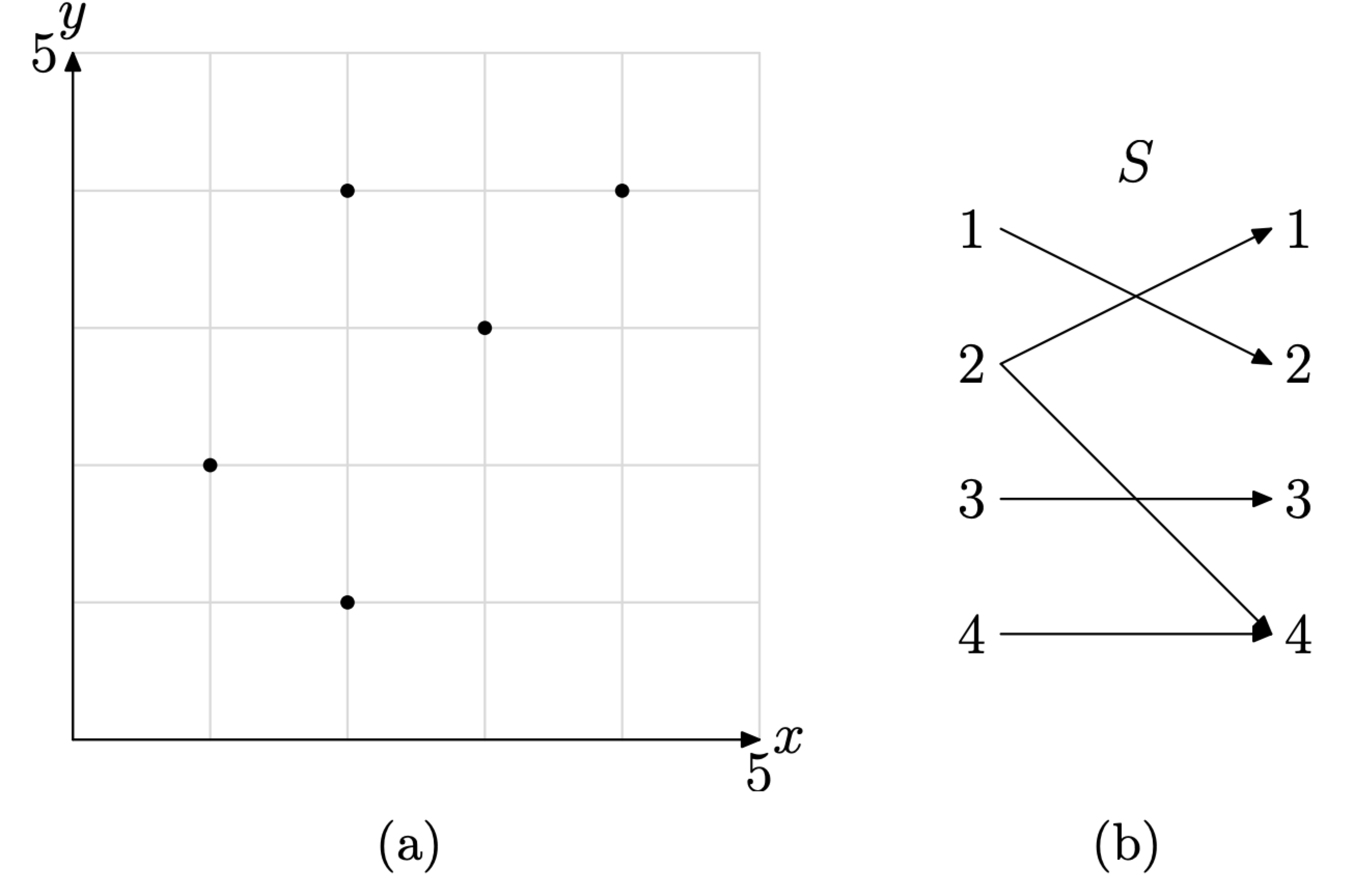
Figura\(\PageIndex{5}\) Un gráfico de la relación S y su diagrama de mapeo correspondiente
Cada objeto en el dominio de S se asigna exactamente a un objeto de rango con una excepción. El objeto de dominio 2 está emparejado con dos objetos de rango, a saber, 1 y 4. En consecuencia, S no es una función.
Este es un buen punto para resumir lo que hemos aprendido sobre las funciones hasta el momento.
Resumen
Una función consta de tres partes:
- un conjunto de objetos que los matemáticos llaman el dominio,
- un segundo conjunto de objetos que los matemáticos llaman el rango,
- y una regla que describe cómo asignar un objeto de rango único a cada objeto del dominio.
La regla puede tomar muchas formas. Por ejemplo, podemos usar conjuntos de pares ordenados, gráficos y diagramas de mapeo para describir la función. En las secciones que siguen, exploraremos otras formas de describir una función, por ejemplo, mediante el uso de ecuaciones y descripciones simples de palabras.
Notación de funciones
Hemos usado la palabra “mapping” varias veces en los ejemplos anteriores. Esta no es una palabra para tomarse a la ligera; es un concepto importante. En el caso del diagrama de mapeo en la Figura\(\PageIndex{5}\) (b), diríamos que el número 1 en el dominio de S está “mapeado” (o “enviado”) al número 2 en el rango de S.
Hay una serie de notaciones diferentes que podríamos usar para indicar que el número 1 en el dominio está “mapeado” o “enviado” al número 2 en el rango. Una posible notación es
\[S : 1 \longrightarrow 2\]
que leeríamos de la siguiente manera: “La relación S mapea (envía) 1 a 2”. En una línea similar, vemos en la Figura\(\PageIndex{5}\) (b) que los objetos de dominio 3 y 4 son mapeados (enviados) a los objetos de rango 3 y 4, respectivamente. En símbolos, escribiríamos
\[\begin{array}{l}{S : 3 \longrightarrow 3, \text { and }} \\ {S : 4 \longrightarrow 4}\end{array}\]
Surge una dificultad cuando examinamos lo que sucede con el objeto de dominio 2. Hay dos posibilidades, ya sea
\[S : 2 \longrightarrow 1\]o\[S : 2 \longrightarrow 4\]
¿Cuál debemos elegir? El 1? ¿O el 4? Así, S no está bien definido y no es una función, ya que no sabemos qué objeto range emparejar con el objeto de dominio 1.
La idea de mapeo nos da una forma alternativa de describir una función. Podríamos decir que una función es una regla que asigna un objeto único en su rango a cada objeto en su dominio. Tomemos por ejemplo, la función que mapea cada número real a su cuadrado. Si nombramos la función f, entonces f mapea 5 a 25, 6 a 36, −7 a 49, y así sucesivamente. En símbolos, escribiríamos
\[f : 5 \longrightarrow 25, \quad f : 6 \longrightarrow 36, \quad \text { and } \quad f :-7 \longrightarrow 49\]
En general, podríamos escribir
\[f : x \longrightarrow x^{2}\]
Tenga en cuenta que cada número real x se mapea a un número único en el rango de f, es decir,\(x^{2}\). En consecuencia, la función f está bien definida. Hemos logrado escribir una regla que defina completamente la función f.
Como otro ejemplo, definamos una función que tome un número real, lo duplique, luego agregue 3. Si nombramos la función g, entonces g tomaría el número 7, lo doblaría, luego agregaría 3. Es decir,
\[g : 7 \longrightarrow 2(7)+3\]
Simplificando,\(g : 7 \longrightarrow 17\). De igual manera, g tomaría el número 9, lo doblaría, luego agregaría 3. Es decir,
\[g : 9 \longrightarrow 2(9)+3\]
Simplificando,\(g : 9 \longrightarrow 21\). En general, g toma un número real x, lo duplica, luego suma tres. En símbolos, escribiríamos
\[g : x \longrightarrow 2 x+3\]
Observe que cada número real x es mapeado por g a un número único en su rango. Por lo tanto, hemos vuelto a definir una regla que define completamente la función g.
Es útil pensar en una función como una máquina. La máquina recibe entrada, la procesa de acuerdo con alguna regla, luego emite un resultado. Algo entra (entrada), luego sale algo (salida). En el caso de la función descrita por la regla\(f : x \longrightarrow x^{2}\), la “f-máquina” recibe la entrada x, luego aplica su “regla cuadrada” a las entradas y salidas\(x^{2}\), como se muestra en la Figura\(\PageIndex{6}\) (a). En el caso de la función descrita por la regla\(g : x \longrightarrow 2 x+3\), la “máquina g” recibe la entrada x, luego aplica las reglas “double”, luego “add 3", en ese orden, luego las salidas\(2x + 3\), como se muestra en la Figura\(\PageIndex{6}\) (b).
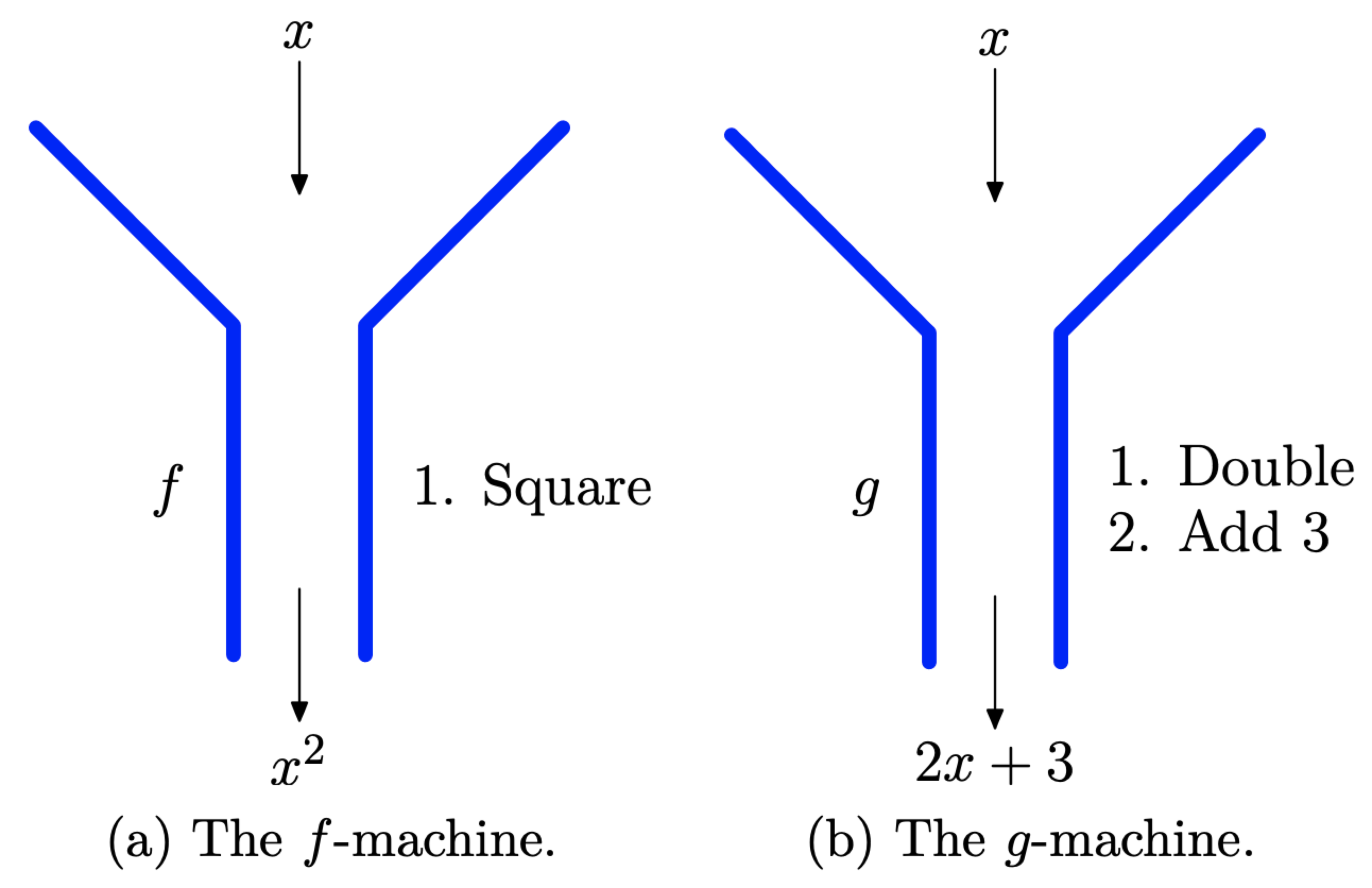
Figura\(\PageIndex{6}\) Función máquinas.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{5}\)
Supongamos que f está definido por la siguiente regla. Por cada número real x,
\[f : x \longrightarrow x^{2}-2 x-3\]
¿Dónde mapea f el número −3? ¿Es f una función?
Solución
Sustituimos −3 por x en la regla por f y obtenemos
\[f :-3 \longrightarrow(-3)^{2}-2(-3)-3\]
Simplificando,
\[f :-3 \longrightarrow 9+6-3\]
o,
\[f :-3 \longrightarrow 12\]
Así, f mapea (envía) el número −3 al número 12. Debe quedar claro que cada número real x será mapeado (enviado) a un número real único, como lo define la regla\(f : x \longrightarrow x^{2}-2 x-3\). Por lo tanto, f es una función.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{6}\)
Supongamos que g está definido por la siguiente regla. Por cada número real x que sea mayor o igual a cero,
\[g : x \longrightarrow \pm \sqrt{x}\]
¿Dónde mapa g el número 4? ¿Es g una función?
Solución
Nuevamente, sustituimos 4 por x en la regla por g y obtenemos
\[g : 4 \longrightarrow \pm \sqrt{4}\]
Simplificando,
\[g : 4 \longrightarrow \pm 2\]
Así, g mapea (envía) el número 4 a dos objetos diferentes en su rango, a saber, 2 y −2. En consecuencia, g no está bien definida y no es una función.
Veamos otro ejemplo
Ejemplo\(\PageIndex{7}\)
Supongamos que tenemos las funciones f y g, definidas por
\[f : x \longrightarrow x^{4}+11 \quad \text { and } \quad g : x \longrightarrow(x+2)^{2}\]
¿Dónde envía g 5?
Solución
En este ejemplo, vemos una clara ventaja de la notación de funciones. Debido a que nuestras funciones tienen nombres distintos, simplemente podemos hacer referencia al nombre de la función que queremos que usen nuestros lectores. En este caso, se nos pregunta dónde envía la función g el número 5, así que sustituimos 5 por x in
\[g : x \longrightarrow(x+2)^{2}\]
Es decir,
\[g : 5 \longrightarrow(5+2)^{2}\]
Simplificando,\(g : 5 \longrightarrow 49\).
Notación Moderna
La notación de funciones es relativamente nueva, con algunos de los primeros simbolismos ocurridos por primera vez en el siglo XVII. En una carta a Leibniz (1698), Johann Bernoulli escribió “Para denotar cualquier función de una cantidad variable x, prefiero usar la letra mayúscula que tenga el mismo nombre X o el griego\(\xi\), pues aparece inmediatamente de qué variable es una función; esto alivia la memoria”.
Los matemáticos son aficionados a la notación\[f : x \longrightarrow x^{2}-2 x\]
porque transmite un sentido de lo que hace una función; es decir, “mapea” o “envía” el número x al número\(x^{2}-2 x\). Esto es lo que hacen las funciones, emparejan cada objeto en su dominio con un objeto único en su rango. Equivalentemente, las funciones “envían” cada objeto en su dominio a un objeto único en su rango.
Sin embargo, en situaciones computacionales comunes, la notación de “flecha” puede ser un poco torpe, por lo que los matemáticos tienden a favorecer una notación ligeramente diferente. En lugar de escribir
\[f : x \longrightarrow x^{2}-2 x\]
los matemáticos tienden a favorecer la notación
\[f(x)=x^{2}-2 x\]
Es importante entender desde el principio que estas dos notaciones diferentes son equivalentes; representan la misma función f, una que empareja cada número real x en su dominio con el número real\(x^{2}-2 x\) en su rango.
La primera notación,\(f : x \longrightarrow x^{2}-2 x\), transmite el sentido de que la función f es un mapeo. Si leemos esta notación en voz alta, deberíamos pronunciarla como “f envía (o mapas) x a”\(x^{2}-2 x\). La segunda notación,\(f(x) = x^{2}-2 x\), se pronuncia “f de x es igual”\(x^{2}-2 x\).
Nota
La frase “f de x” es lamentable, ya que nuestros lectores podrían recordar haber sido entrenados desde muy temprana edad para emparejar la palabra “de” con la operación de multiplicación. Por ejemplo, 1/2 de 12 es 6, como en\(1 / 2 \times 12=6\). Sin embargo, en el contexto de la notación de funciones, aunque f (x) se lea en voz alta como “f de x”, no significa “f por x”. En efecto, si nos recordamos que la notación\(f(x)=x^{2}-2 x\) es equivalente a la notación\(f : x \longrightarrow x^{2}-2 x\), entonces aunque pudiéramos decir “f de x”, deberíamos estar pensando “f envía x” o “f maps x”. No deberíamos estar pensando “f veces x”.
Ahora, veamos cómo opera cada una de estas notaciones en el número 5. En el primer caso, usando la notación de “flecha”,
\[f : x \longrightarrow x^{2}-2 x\]
Para encontrar donde f envía 5, sustituimos 5 por x de la siguiente manera.
\[f : 5 \longrightarrow(5)^{2}-2(5)\]
Simplificando,\(f : 5 \longrightarrow 15\). Ahora bien, debido a que ambas notaciones son equivalentes, para calcular f (5), volvemos a sustituir 5 por x in
\[f(x)=x^{2}-2 x\]
Por lo tanto,
\[f(5)=(5)^{2}-2(5)\]
Simplificando,\(f(5)=15\). Este resultado se lee en voz alta como “f de 5 es igual a 15”, pero queremos estar pensando “f envía de 5 a 15”.
Veamos ejemplos que utilizan esta notación moderna.
Ejemplo\(\PageIndex{8}\)
Dado\(f(x)=x^{3}+3 x^{2}-5,\) determinar\(f(-2)\)
Solución
Simplemente sustituya −2 por x. Es decir,
\[\begin{aligned} f(-2) &=(-2)^{3}+3(-2)^{2}-5 \\ &=-8+3(4)-5 \\ &=-8+12-5 \\ &=-1 \end{aligned}\]
Así,\(f(−2) = −1\). Nuevamente, aunque esto se pronuncia “f de −2 es igual a −1", todavía deberíamos estar pensando “f envía −2 a −1".
Ejemplo\(\PageIndex{9}\)
Dado\[f(x)=\frac{x+3}{2 x-5}\] determinar f (6).
Solución
Simplemente sustituya 6 por x. Es decir,\[\begin{aligned} f(6) &=\frac{6+3}{2(6)-5} \\ &=\frac{9}{12-5} \\ &=\frac{9}{7} \end{aligned}\]
Así,\(f(6) = 9/7\). Nuevamente, a pesar de que esto se pronuncia “f de 6 es igual a 9/7", deberíamos seguir pensando “f envía 6 a 9/7".
Ejemplo\(\PageIndex{10}\)
Dado\(f(x)=5 x-3,\) determinar\(f(a+2)\).
Solución
Si estamos pensando en términos de notación cartográfica, entonces\[f : x \longrightarrow 5 x-3\]
Piense en este mapeo como una “máquina”. Lo que sea que pongamos en la máquina, primero se multiplica por 5, luego se resta 3 del resultado, como se muestra en la Figura\(\PageIndex{7}\). Por ejemplo, si ponemos un 4 en la máquina, entonces la regla de función requiere que multipliquemos la entrada 4 por 5, luego restemos 3 del resultado. Es decir,
\[f : 4 \longrightarrow 5(4)-3\]
Simplificando,\(f : 4 \longrightarrow 17\)
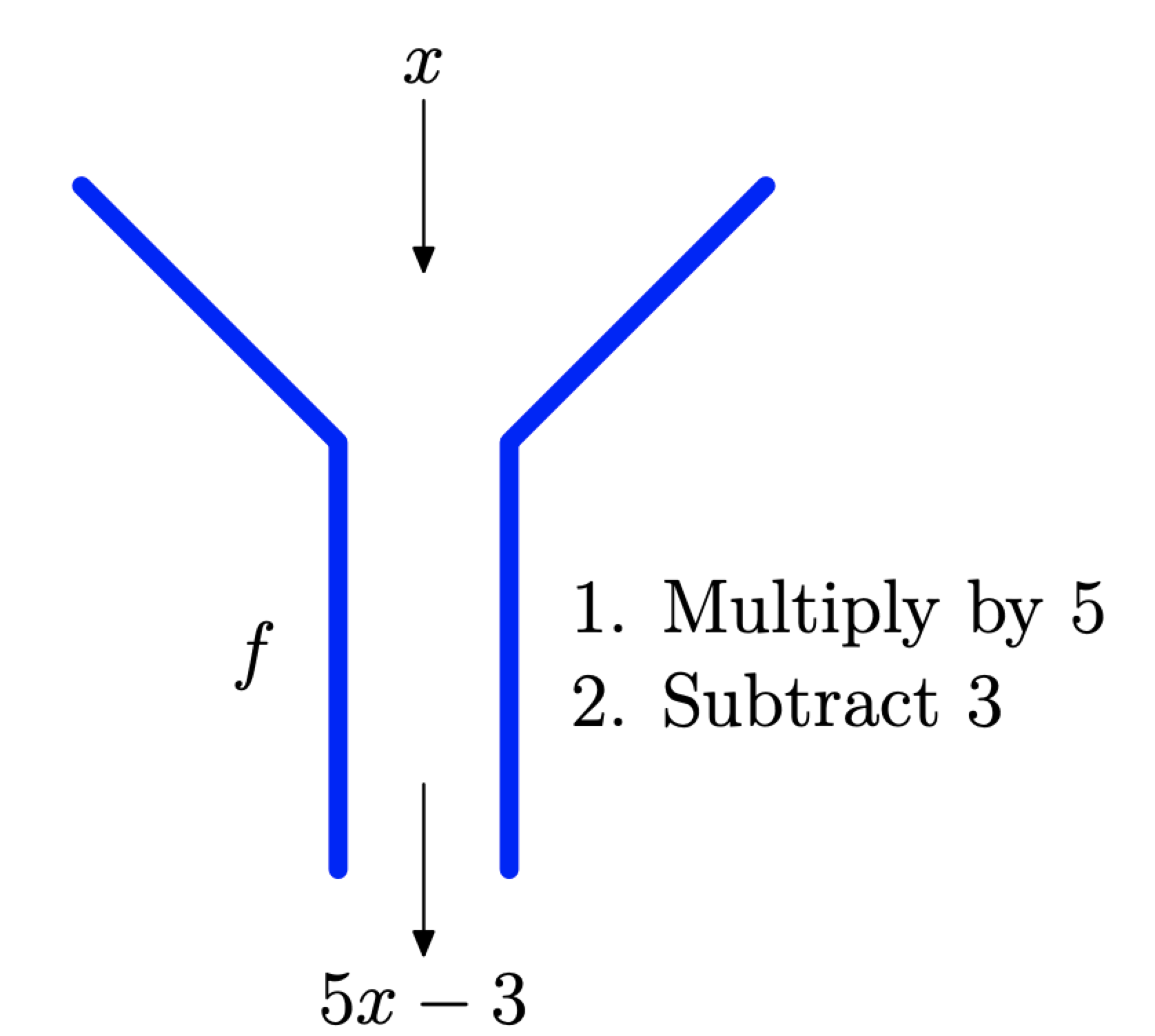
Figura\(\PageIndex{7}\). El multiplicar por 5 luego restar 3 máquina.
De igual manera, si ponemos un a + 2 en la máquina, entonces la regla de función requiere que multipliquemos la entrada a + 2 por 5, luego restemos 3 del resultado. Es decir,
\[f : a+2 \longrightarrow 5(a+2)-3\]
Usando la notación de funciones modernas, escribiríamos
\[f(a+2)=5(a+2)-3\]
Tenga en cuenta que esta es nuevamente una simple sustitución, donde reemplazamos cada ocurrencia de x en la fórmula\(f(x) = 5x − 3\) con la expresión a + 2. Finalmente, use la propiedad distributiva para multiplicar primero por 5, luego restar 3.
\[\begin{aligned} f(a+2) &=5 a+10-3 \\ &=5 a+7 \end{aligned}\]
A menudo necesitaremos sustituir el resultado de una evaluación de función en una segunda función para la evaluación. Veamos un ejemplo.
Ejemplo\(\PageIndex{11}\)
Dadas dos funciones definidas por\(f(x) = 3x + 2\) y\(g(x) = 5 − 4x\), find f (g (2)).
Solución
Los paréntesis anidados en la expresión f (g (2)) funcionan de la misma manera que lo hacen con las expresiones anidadas. La regla es trabajar primero los símbolos de agrupación más internos, procediendo hacia afuera a medida que trabajas. Primero evaluaremos g (2), luego evaluaremos f en el resultado.
Empezamos. Primero, evalúe g (2) sustituyendo 2 por x en la ecuación definitoria\(g(x) = 5 − 4x\). Tenga en cuenta eso\(g(2) = 5 − 4(2)\), luego simplifique.
\[f(g(2))=f(5-4(2))=f(5-8)=f(-3)\]
Para completar la evaluación, sustituimos −3 por x en la ecuación definitoria\(f(x) = 3x + 2\), luego simplificamos.
\[f(-3)=3(-3)+2=-9+2=-7\]
De ahí,\(f(g(2))=-7\).
Es convencional disponer la obra en un bloque contiguo, de la siguiente manera.
\[\begin{aligned} f(g(2)) &=f(5-4(2)) \\ &=f(-3) \\ &=3(-3)+2 \\ &=-7 \end{aligned}\]
Puedes acortar aún más la tarea si estás dispuesto a hacer la sustitución y simplificación de funciones en tu cabeza. Primero, evaluar g a 2, luego f en el resultado.
\[f(g(2))=f(-3)=-7\]
Veamos otro ejemplo de esta forma única de combinar funciones.
Ejemplo\(\PageIndex{12}\)
Dado\(f(x) = 5x + 2\) y\(g(x) = 3 − 2x\), evaluar\(g(f(a))\) y simplificar el resultado.
Solución
Se trabaja\(g(f(a))\) primero la evaluación de la función interna en la expresión. Así, para evaluar f (a), sustituimos a x en la definición\(f(x) = 5x + 2\) para obtener
\[g(f(a))=g(5 a+2)\]
Ahora tenemos que evaluar\(g(5a + 2)\). Para ello,\(5a + 2\) sustituimos x en la definición\(g(x) = 3 − 2x\) para obtener
\[g(5 a+2)=3-2(5 a+2)\]
Podemos ampliar este último resultado y simplificar. Por lo tanto,
\[g(f(a))=3-10 a-4=-10 a-1\]
Nuevamente, es convencional disponer la obra en un bloque continuo, de la siguiente manera.
\[\begin{aligned} g(f(a)) &=g(5 a+2) \\ &=3-2(5 a+2) \\ &=3-10 a-4 \\ &=-10 a-1 \end{aligned}\]
De ahí,\(g(f(a))=-10 a-1\).
Extracción del dominio de una función
Hemos visto que el dominio de una relación o función es el conjunto de todas las primeras coordenadas de sus pares ordenados. Sin embargo, si una relación funcional es definida por una ecuación como\(f(x) = 3x − 4\), entonces no es práctico enumerar todos los pares ordenados definidos por esta relación. Para cualquier valor x real, obtienes un par ordenado. Por ejemplo, si x = 5, entonces\(f(5) = 3(5) − 4 = 11\), conduce al par ordenado (5, f (5)) o (5, 11). Como puede ver, el número de tales pares ordenados es infinito. Por cada nuevo valor x, obtenemos otro valor de función y otro par ordenado.
Por lo tanto, es más fácil dirigir nuestra atención a los valores de x que arrojan respuestas numéricas reales en la ecuación\(f(x) = 3x − 4\). Esto lleva a la siguiente idea clave.
Definición
Si una función es definida por una ecuación, entonces el dominio de la función es el conjunto de “valores x permisibles”, los valores que producen una respuesta numérica real definida por la ecuación.
A veces nos gusta decir que el dominio de una función es el conjunto de “OK valores x para usar en la ecuación”. Por ejemplo, si definimos una función con la regla\(f(x) = 3x − 4\), es inmediatamente evidente que podemos usar cualquier valor que queramos para x en la regla\(f(x) = 3x − 4\). Así, el dominio de f es todo números reales. Podemos escribir que el dominio\(D=\mathbb{R}\), o podemos usar notación de intervalo y escribir que el dominio\(D=(-\infty, \infty)\).
No es el caso de que x pueda ser cualquier número real en la función definida por la regla\(f(x)=\sqrt{x}\). No es posible tomar la raíz cuadrada de un número negativo.2 Por lo tanto, x debe ser cero o un número real positivo. En notación set-builder, podemos describir el dominio con\(D=\{x : x \geq 0\}\). En notación de intervalos, escribimos\(D=[0, \infty)\).
También debemos ser conscientes de que no podemos dividir por cero. Si definimos una función con la regla\(f(x)=x /(x-3)\), inmediatamente vemos que x = 3 pondrá un cero en el denominador. La división por cero no está definida. Por lo tanto, 3 no está en el dominio de f. Ningún otro valor x causará un problema. El dominio de f se describe mejor con notación set-builder como\(D=\{x : x \neq 3\}\).
Funciones sin fórmulas
En la sección anterior, definimos funciones por medio de una fórmula, por ejemplo, como en
\[f(x)=\frac{x+3}{2-3 x}\]
Euler estaría satisfecho con esta definición, pues como hemos dicho anteriormente, Euler pensó en las funciones como expresiones analíticas.
Sin embargo, realmente no es necesario proporcionar una expresión o fórmula para definir una función. Hay otras formas que podemos usar para expresar una relación funcional: una gráfica, una tabla, o incluso una descripción narrativa. Lo único que es realmente importante es el requisito de que la función esté bien definida, y por “bien definida”, queremos decir que cada objeto en el dominio de la función está emparejado con uno y solo un objeto en su rango.
Como ejemplo, veamos una función especial\(\pi\) sobre los números naturales,3 que devuelve el número de primos menor o igual que un número natural dado. Por ejemplo, los primos menores o iguales que el número 23 son 2, 3, 5, 7, 11, 13, 17, 19 y 23, nueve números en total. Por lo tanto, el número de primos menor o igual a 23 es nueve. En símbolos, escribiríamos
\[\pi(23)=9\]
Obsérvese la ausencia de una fórmula en la definición de esta función. En efecto, la definición es de carácter descriptivo, por lo que podríamos escribir
\[\pi(n)=\text { number of primes less than or equal to } n\]
Lo importante no es cómo definimos esta función especial π, sino el hecho de que esté bien definida; es decir, para cada número natural n, hay un número fijo de primos menor o igual a n Así, cada número natural en el dominio de π se empareja con uno y solo un número en su rango.
Ahora bien, solo porque nuestra función no proporciona una expresión para calcular el número de primos menor o igual a un número natural dado n, no impide que los matemáticos busquen tal fórmula. Euclides de Alejandría (325-265 a.C.), matemático griego, demostró que el número de primos es infinito, pero fue el matemático y científico alemán, Johann Carl Friedrich Gauss (1777-1855), quien primero propuso que el número de primos menor o igual a n puede aproximarse por la fórmula
\[\pi(n) \approx \frac{n}{\ln n}\]
donde ln n es el “logaritmo natural” de n (a explicar en el Capítulo 9). Esta aproximación mejora cada vez mejor con valores cada vez mayores de n. La fórmula fue refinada por Gauss, quien no aportó una prueba, y el problema se conoció como el Teorema del Número Primo. No fue sino hasta 1896 que Jacques Salomon Hadamard (1865-1963) y Charles Jean Gustave Nicolas Barón de la Vallee Poussin (1866-1962), trabajando de manera independiente, proporcionaron una prueba del Teorema del Número Primo.