2.5: Transformaciones verticales

Última actualización
Guardar como PDF

Page ID: 110842

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En esta sección estudiamos el arte de las transformaciones: escalamientos, reflexiones y traducciones. Vamos a restringir nuestra atención a las transformaciones en la dirección vertical o y. Nuestro objetivo es aplicar ciertas transformaciones a la ecuación de una función, luego preguntar qué efecto tiene en la gráfica de la función.

Comenzamos nuestra tarea con un ejemplo que requiere que leamos la gráfica de una función para capturar varios puntos clave que se encuentran en la gráfica de la función.

Ejemplo$\PageIndex{1}$

Considera la gráfica de f presentada en la Figura$\PageIndex{1}$ (a). Utilice la gráfica de f para completar la tabla de la Figura$\PageIndex{1}$ (b).

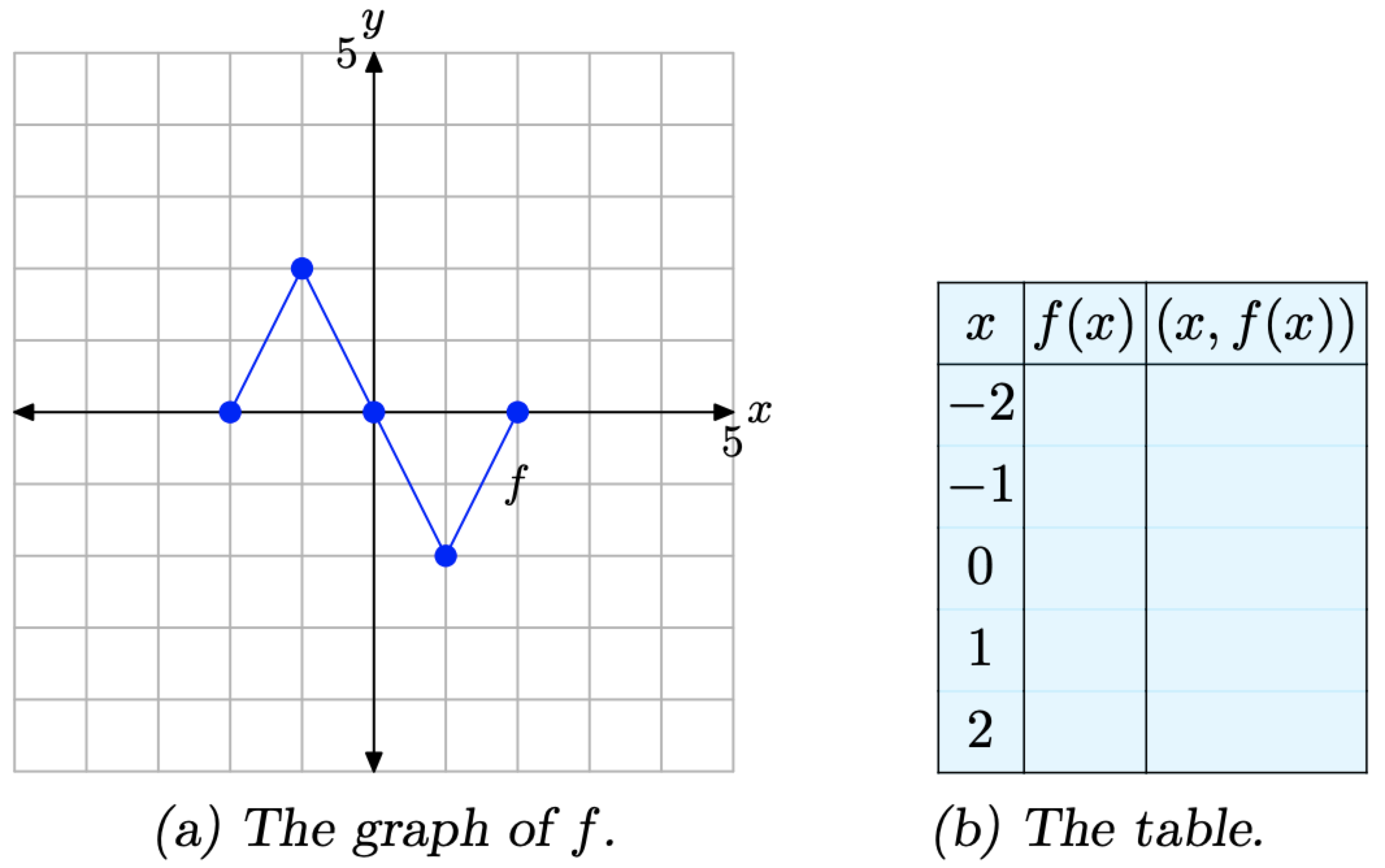
$WeChat231fdb846a5a57b3b7017acff5673b7e.png$

Figura$\PageIndex{1}$. Lectura de valores clave de la gráfica de f.

Solución

Para calcular f (−1), ubicaríamos −1 en el eje x, dibujaríamos una flecha vertical a la gráfica de f, luego una flecha horizontal al eje y, como se muestra en la Figura$\PageIndex{2}$ (a). El valor y de este destino final es el valor de f (−1). Es decir, f (−1) = 2. Esto nos permite completar una entrada en la tabla, como se muestra en la Figura$\PageIndex{2}$ (b). Continuar de esta manera para completar todas las entradas en la tabla. El resultado se muestra en la Figura$\PageIndex{2}$ (c).

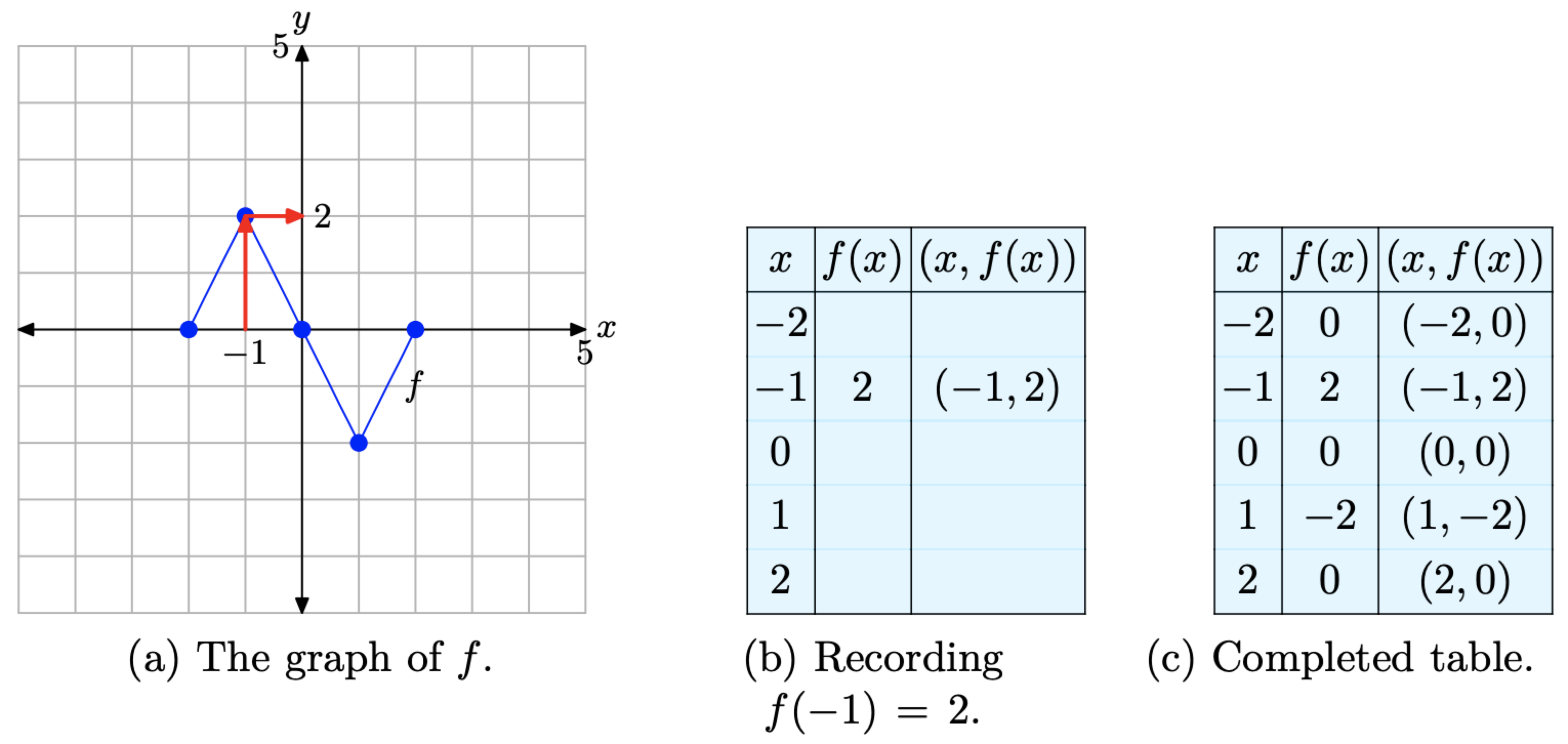
$WeChat3ca39b7081394e6f8965adb0dd945e1e.png$

Figura$\PageIndex{2}$. Grabación de coordenadas de puntos en la gráfica de f en las tablas.

Escalado vertical

En la narrativa que sigue, tendremos necesidad repetida de la gráfica en la Figura$\PageIndex{2}$ (a) y la tabla en la Figura$\PageIndex{2}$ (c). Caracterizan la función básica que será el punto de partida para los conceptos de escalado, reflexión y traducción que desarrollamos en esta sección. En consecuencia, coloquemos uno al lado del otro para enfatizarlos en la Figura$\PageIndex{3}$.

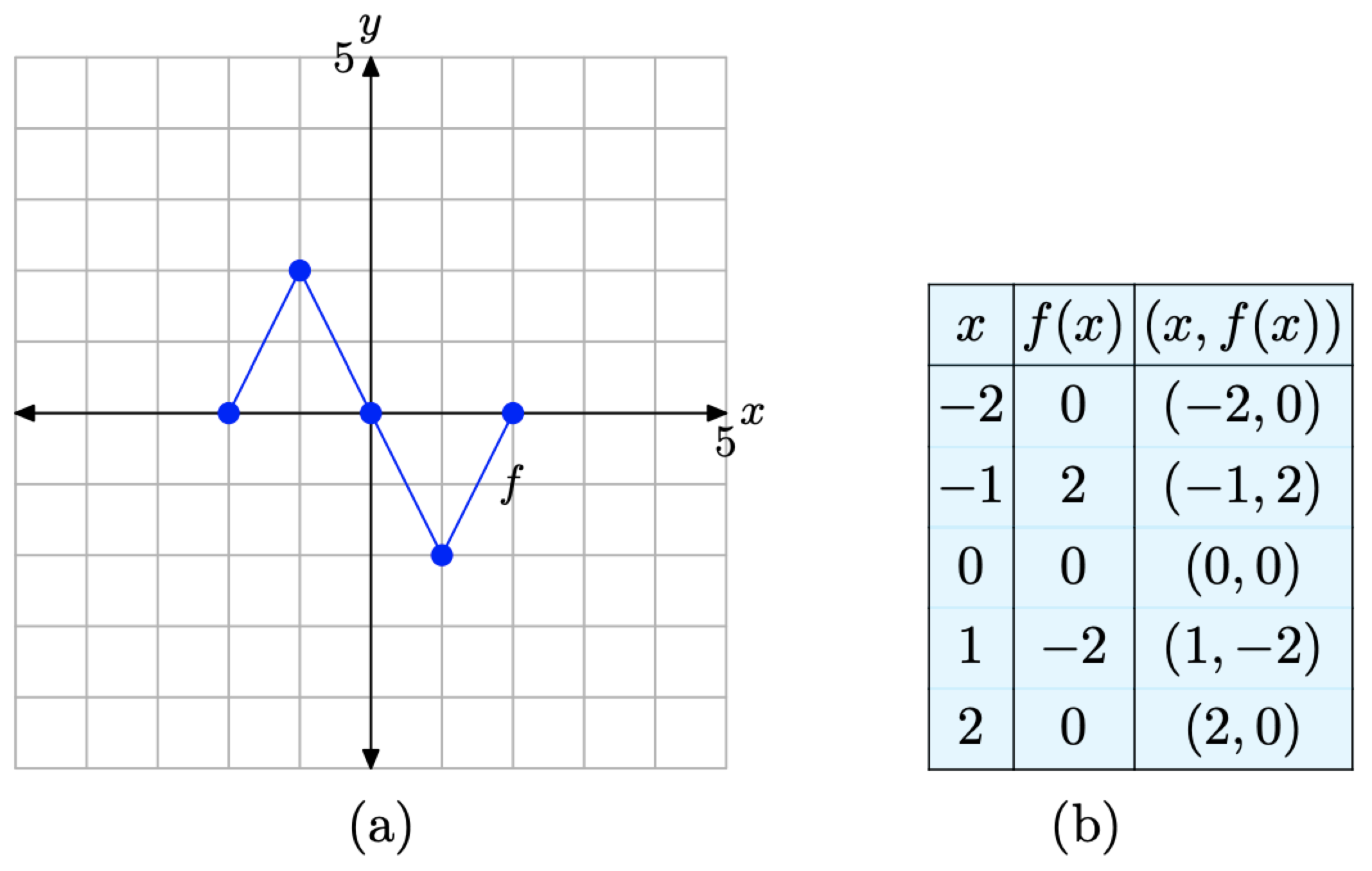
$WeChat121beb889b53c2b82eca4e9b45e08663.png$

Figura$\PageIndex{3}$. La gráfica original de f y una tabla de puntos clave en la gráfica de f.

Ahora vamos a escalar la gráfica de f en dirección vertical.

Ejemplo$\PageIndex{2}$

Si y = f (x) tiene la gráfica mostrada en la Figura$\PageIndex{3}$ (a), esboce la gráfica de y = 2f (x).

Solución

¿Qué hacemos cuando nos encontramos con una gráfica cuya forma no estamos seguros? La respuesta a esta pregunta es que trazamos algunos puntos que satisfacen la ecuación para tener una idea de la forma de la gráfica. Con ese pensamiento en mente, evaluemos la función y = 2f (x) a x = −2.

La letra f se refiere a la función original mostrada en la Figura$\PageIndex{3}$ (a) y la tabla de la Figura$\PageIndex{3}$ (b) contiene los valores de esa función en los valores dados de x Así, al calcular y = 2f (−2), el primer paso es buscar el valor de f (−2) en la tabla de la Figura$\PageIndex{3}$ (b). Ahí encontramos que f (−2) = 0. Así, podemos escribir\[y=2 f(-2)=2(0)=0\]

De manera similar, evaluemos la función y = 2f (x) a x = −1. Primero, busque el valor de f (−1) en la tabla de la Figura$\PageIndex{3}$ (b). Ahí encontramos que f (−1) = 2. Así, podemos escribir\[y=2 f(-1)=2(2)=4\]

Terminamos evaluando la función y = 2f (x) en x = 0, 1 y 2. Cada vez que necesite evaluar la función f en un número, tome el resultado de la tabla o gráfica de la Figura 3. Lo que sigue son las evaluaciones de y = 2f (x) a x = −2, −1, 0, 1 y 2.

\[\begin{array}{l}{y=2 f(-2)=2(0)=0} \\ {y=2 f(-1)=2(2)=4} \\ {y=2 f(0)=2(0)=0} \\ {y=2 f(1)=2(-2)=-4} \\ {y=2 f(2)=2(0)=0}\end{array}\]

Podemos organizar estos resultados en una tabla que se muestra en la Figura$\PageIndex{4}$ (b), luego trazarlos en la figura mostrada en la Figura$\PageIndex{4}$ (a).

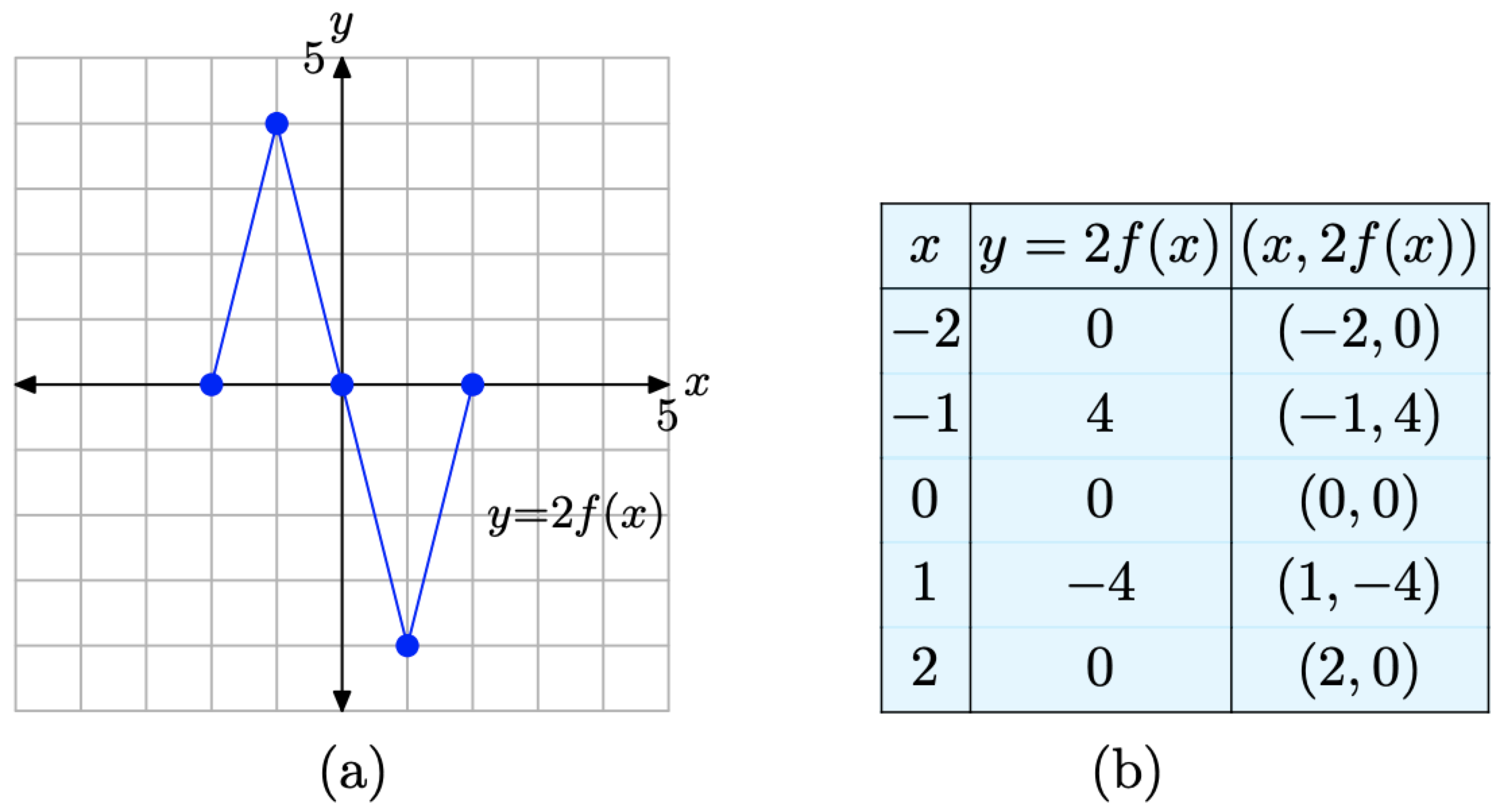
$WeChat8bab2e9940b274f4aa16178936431d15.png$

Figura$\PageIndex{4}$. Los puntos en la tabla son puntos en la gráfica de y = 2f (x).

En este punto, hay una serie de comparaciones que puedes hacer.

Comparar los datos en las tablas de la Figura$\PageIndex{3}$ (b) y Figura$\PageIndex{4}$ (b). Tenga en cuenta que los valores x son idénticos. En ambas tablas, x = −2, −1, 0, 1 y 2. Sin embargo, tenga en cuenta que cada valor y en la tabla de la Figura$\PageIndex{4}$ (b) es precisamente el doble del valor y correspondiente en la tabla de la Figura$\PageIndex{3}$ (b).
Compare las gráficas de la Figura$\PageIndex{3}$ (a) y la Figura$\PageIndex{4}$ (a). Obsérvese que el valor y de cada punto en la gráfica de y = 2f (x) en la Figura$\PageIndex{4}$ (a) es precisamente el doble del valor y del punto correspondiente en la Figura$\PageIndex{3}$ (a).

Anote el resultado. La gráfica de y = 2f (x) se ha estirado verticalmente (alejándose del eje x), tanto positiva como negativamente, por un factor de 2.

Veamos otro ejemplo.

Ejemplo$\PageIndex{3}$

Si y = f (x) tiene la gráfica mostrada en la Figura$\PageIndex{3}$ (a), esboce la gráfica de y = (1/2) f (x).

Solución

Comencemos evaluando la función y = (1/2) f (x) a x = −2. Primero, busque el valor de f (−2) en la tabla de la Figura$\PageIndex{3}$ (b). Ahí encontramos que f (−2) = 0. Así, podemos escribir\[y=(1 / 2) f(-2)=(1 / 2)(0)=0\]

De manera similar, evaluemos la función y = (1/2) f (x) a x = −1. Primero, busque el valor de f (−1) en la tabla de la Figura$\PageIndex{3}$ (b). Ahí encontramos que f (−1) = 2. Así, podemos escribir\[y=(1 / 2) f(-1)=(1 / 2)(2)=1\]

Continuando de esta manera, podemos evaluar la función y = (1/2) f (x) en x = 0, 1 y 2.

\[\begin{array}{l}{y=(1 / 2) f(0)=(1 / 2)(0)=0} \\ {y=(1 / 2) f(1)=(1 / 2)(-2)=-1} \\ {y=(1 / 2) f(2)=(1 / 2)(0)=0}\end{array}\]

Los resultados se registran en la tabla de la Figura$\PageIndex{5}$ (b). En lugar de duplicar cada valor de y como lo hizo la función y = 2f (x) en Ejemplo$\PageIndex{2}$, esta función y = (1/2) f (x) reduce a la mitad cada valor de y La gráfica de y = (1/2) f (x) y una tabla de puntos clave en la gráfica se presentan en las Figuras$\PageIndex{5}$ (a) y (b), respectivamente.

Nuevamente, hay una serie de comparaciones.

Comparar los datos en las tablas de la Figura$\PageIndex{5}$ (b) y Figura$\PageIndex{3}$ (b). Tenga en cuenta que los valores x son idénticos. En ambas tablas x = −2, −1, 0, 1 y 2. Sin embargo, tenga en cuenta que cada valor y en la tabla de la Figura$\PageIndex{5}$ (b) es precisamente la mitad del valor y correspondiente en la tabla de la Figura$\PageIndex{3}$ (b).
Al comparar la gráfica de y = (1/2) f (x) en la Figura$\PageIndex{5}$ (a) con la gráfica original de y = f (x) en la Figura$\PageIndex{3}$ (a), tenga en cuenta que cada punto de la gráfica de y = (1/2) f (x) tiene un valor y que es precisamente la mitad del valor y correspondiente en la gráfica original de y = f (x) en la Figura$\PageIndex{3}$ (a).

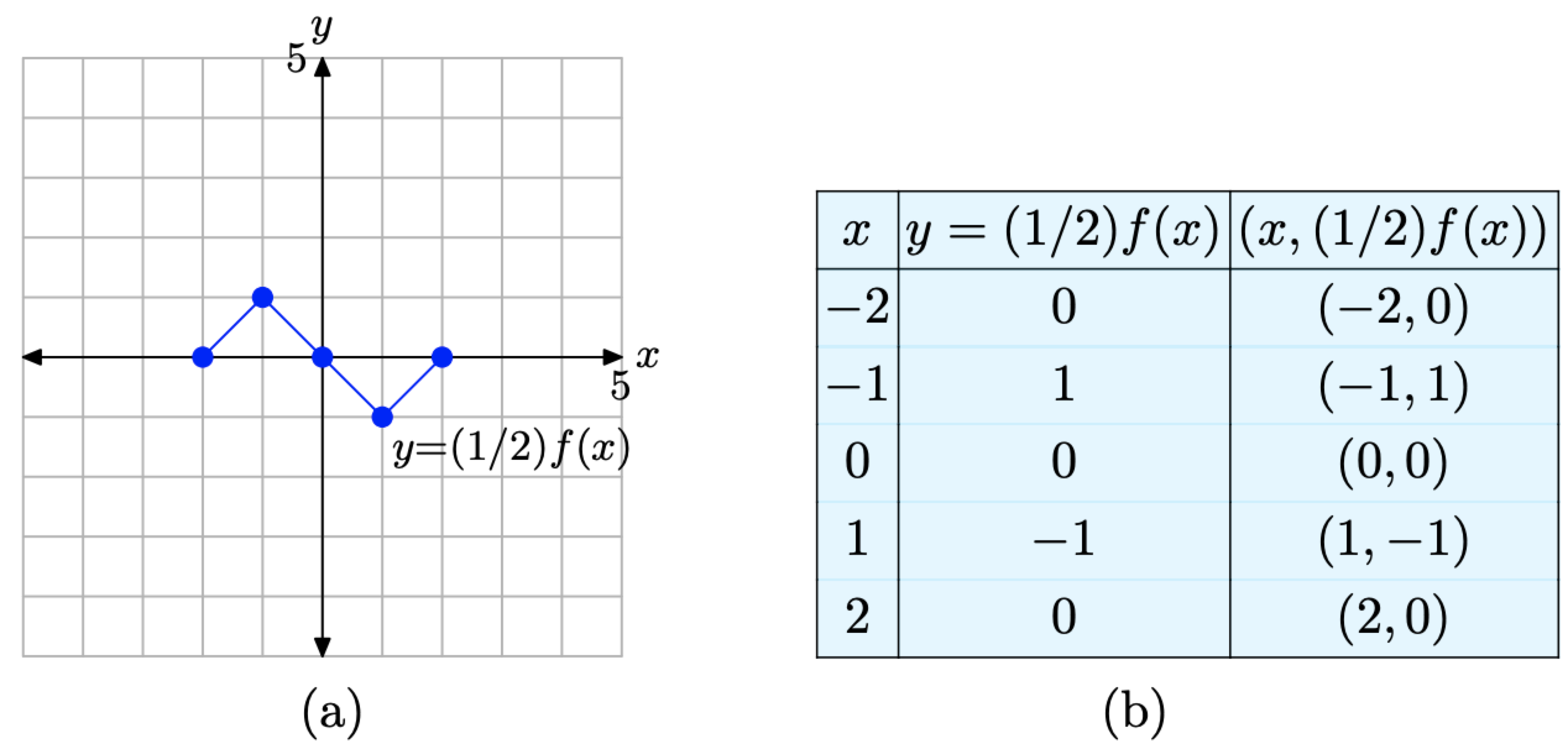
$WeChat4c2b144dcb3ff59dc8405501f815a912.png$

Figura$\PageIndex{5}$. Los puntos en la tabla son puntos en la gráfica de y = (1/2) f (x).

Anote el resultado. La gráfica de f se ha comprimido verticalmente (hacia el eje x), tanto positiva como negativamente, por un factor de 2.

Resumimos nuestros hallazgos.

Un Resumen Visual — Escalado Vertical.

Considera las imágenes en la Figura$\PageIndex{6}$.

En la Figura$\PageIndex{6}$ (a), vemos representado el gráfico de la función original y = f (x).
En la Figura$\PageIndex{6}$ (b), nótese que cada punto clave en la gráfica de y = 2f (x) tiene un valor y que es precisamente el doble del valor y del punto correspondiente en la gráfica de y = f (x) en la Figura$\PageIndex{6}$ (a).
En la Figura$\PageIndex{6}$ (c), observe que cada punto clave en la gráfica de y = (1/2) f (x) tiene un valor y que es precisamente la mitad del valor y del punto correspondiente en la gráfica de y = f (x) en la Figura$\PageIndex{6}$ (a).
Tenga en cuenta que el valor x de cada punto transformado sigue siendo el mismo.

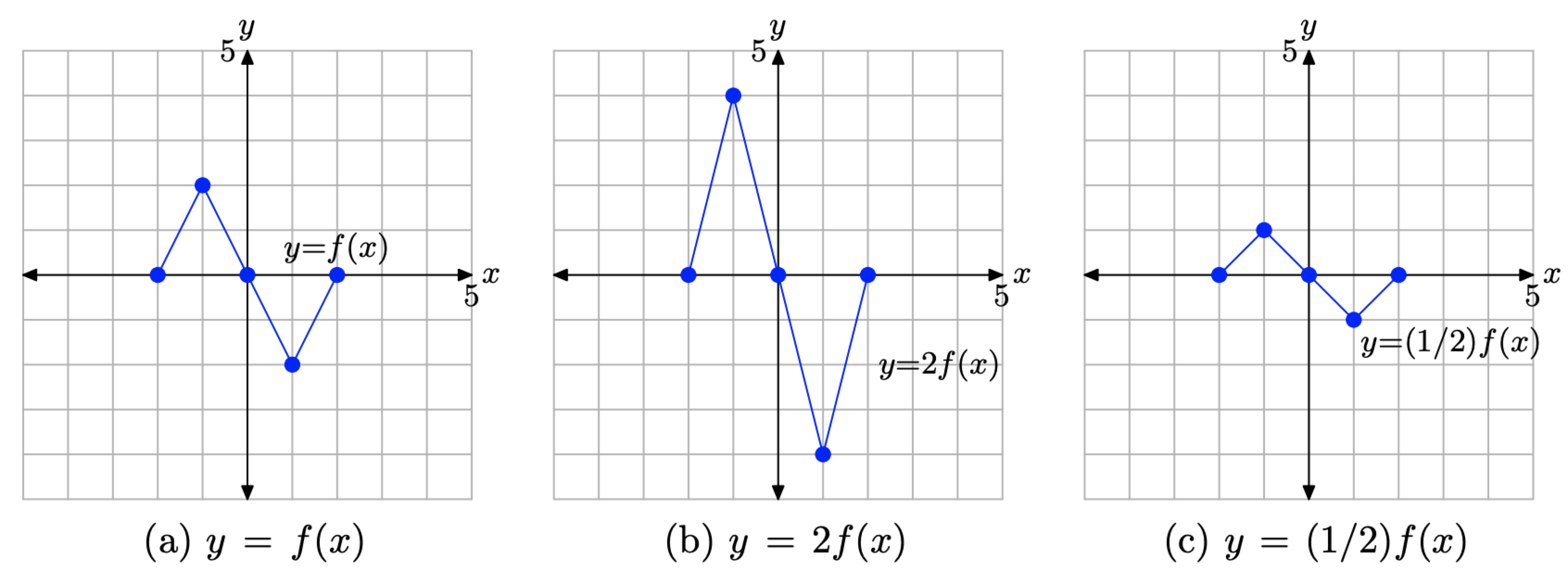
$WeChat45e5c0f5b7d7ed643f9c06f046d84386.png$

Figura$\PageIndex{6}$. La gráfica de y = 2f (x) se estira verticalmente (alejándose del eje x) por un factor de 2. La gráfica de y = (1/2) f (x) comprime verticalmente (hacia el eje x) en un factor de 2.

El resumen visual de la Figura$\PageIndex{6}$ hace que bosquejar las gráficas de y = 2f (x) e y = (1/2) f (x) sea una tarea fácil.

Dada la gráfica de y = f (x), para bosquejar la gráfica de y = 2f (x), simplemente tome cada punto de la gráfica de y = f (x) y duplique su valor y, manteniendo el mismo valor x.
Dada la gráfica de y = f (x), para bosquejar la gráfica de y = (1/2) f (x), simplemente tomar cada punto de la gráfica de y = f (x) y reducir a la mitad su valor y, manteniendo el mismo valor x.

Siga los mismos procedimientos para otros factores de escalado. Por ejemplo, en el caso de y = 3f (x), tomar cada punto de la gráfica de y = f (x) y multiplicar su valor y por 3, manteniendo el mismo valor x. Por otro lado, para dibujar la gráfica de y = (1/3) f (x), tomar cada punto de la gráfica de f y multiplicar su valor y por 1/3, manteniendo el mismo valor y.

En general, podemos exponer lo siguiente.

resumen

Supongamos que se nos da la gráfica de y = f (x).

Si a > 1, entonces la gráfica de y = af (x) se estira verticalmente (alejándose del eje x), tanto positiva como negativamente, por un factor de a.
Si 0 < a < 1, entonces la gráfica de y = af (x) se comprime verticalmente (hacia el eje x), tanto positiva como negativamente, por un factor de 1/a.

El segundo ítem de Resumen merece una palabra explicativa. Compara la forma general y = af (x) con la función de Ejemplo$\PageIndex{3}$, y = (1/2) f (x). En este caso, a = 1/2, entonces\[\frac{1}{a}=\frac{1}{1 / 2}=1 \times 2=2\]

El segundo ítem dice que cuando 0 < a < 1, la gráfica de y = af (x) se comprime verticalmente por un factor de 1/a.De hecho, esto es exactamente lo que sucede en el caso de y = (1/2) f (x), que se comprime por un factor de 1/ (1/2), o 2.

Reflexiones Verticales

Para mayor comodidad, comenzamos repitiendo la gráfica original de y = f (x) y sus datos acompañantes.

Ahora vamos a reflejar la gráfica en la dirección vertical (a través del eje x).

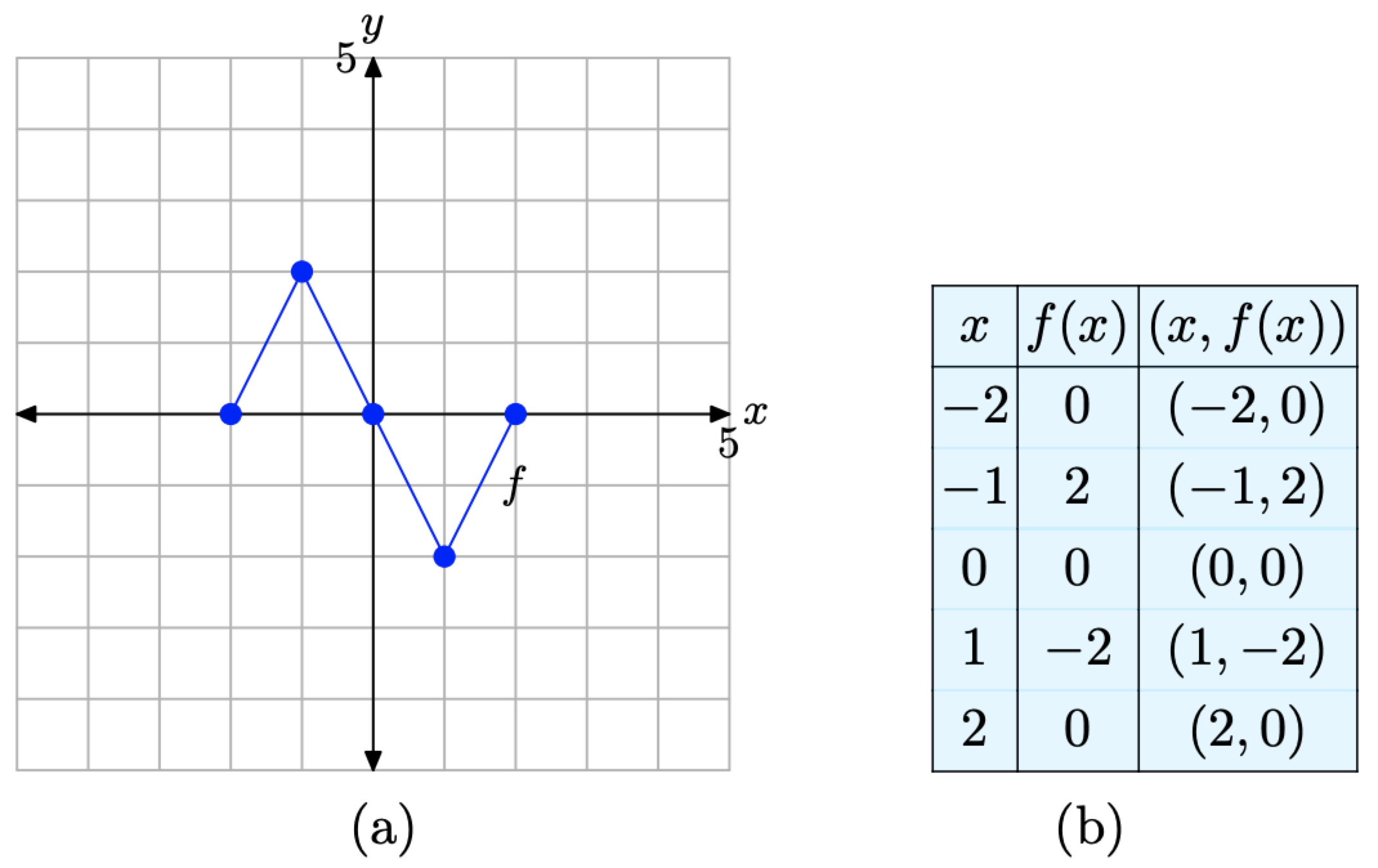
$WeChat28f413c47b5cadc6612b803db3aa404a.png$

Figura$\PageIndex{7}$. La gráfica original de f y una tabla de puntos clave en la gráfica de f.

Ejemplo$\PageIndex{4}$

Si y = f (x) tiene la gráfica mostrada en la Figura$\PageIndex{7}$ (a), esboce la gráfica de y = −f (x).

Solución

Para configurar una tabla de puntos en preparación para la gráfica de y = −f (x), usaremos exactamente los mismos valores de x que ves en la tabla de la Figura$\PageIndex{7}$ (b), es decir, x = −2, −1, 0, 1 y 2. Para evaluar y = −f (x) en el primer valor de x, concretamente x = −2, hacemos el siguiente cálculo,

\[y=-f(-2)=-(0)=0\]

donde hemos usado el hecho de que f (−2) = 0 de la tabla de la Figura$\PageIndex{7}$ (b). De manera similar, evaluamos y = −f (x) en cada uno de los valores restantes de x, es decir, x = −1, 0, 1 y 2.

\[\begin{aligned} y &=-f(-1)=-(2)=-2 \\ y &=-f(0)=-(0)=0 \\ y &=-f(1)=-(-2)=2 \\ y &=-f(2)=-(0)=0 \end{aligned}\]

Ensamblamos estos puntos en la tabla de la Figura$\PageIndex{8}$ (b) y los trazamos en la Figura$\PageIndex{8}$ (a).

Obsérvese que la gráfica de y = −f (x) en la Figura$\PageIndex{8}$ (a) es un reflejo de la gráfica de y = f (x) en la Figura$\PageIndex{7}$ (a) a través del eje x.

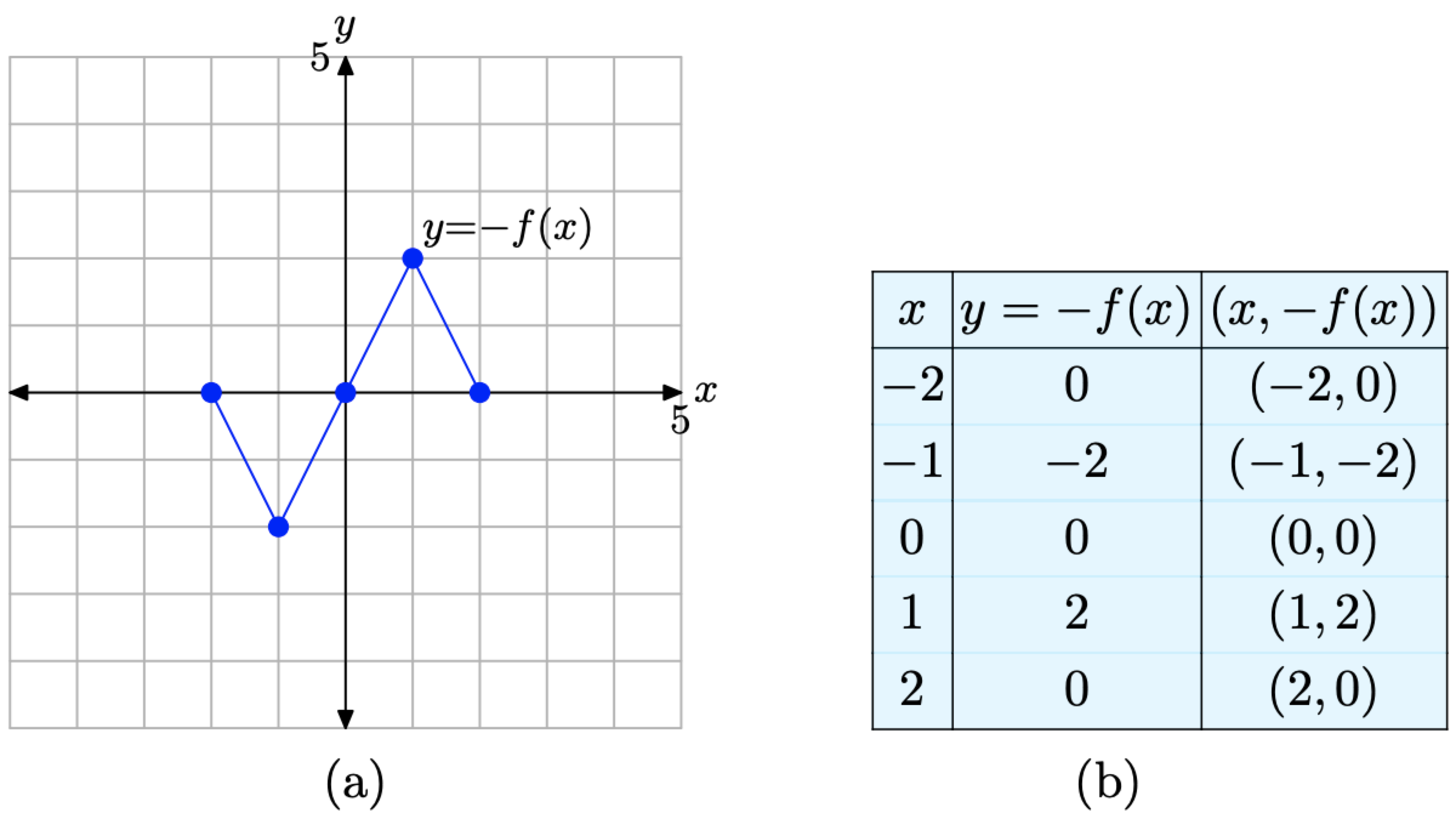
$WeChat8ecae9b9acd1d041ee2ca7bb5f9ff5ba.png$

Figura$\PageIndex{8}$. La gráfica de y = −f (x) y una tabla de puntos clave en la gráfica.

Resumimos lo que hemos aprendido sobre las reflexiones verticales.

Un Resumen Visual — Reflexiones Verticales

Considera las imágenes en la Figura$\PageIndex{9}$.

En la Figura$\PageIndex{9}$ (a), vemos en la imagen la gráfica original de y = f (x).
En la Figura$\PageIndex{9}$ (b), la gráfica de y = −f (x) es un reflejo de la gráfica de y = f (x) a través del eje x.

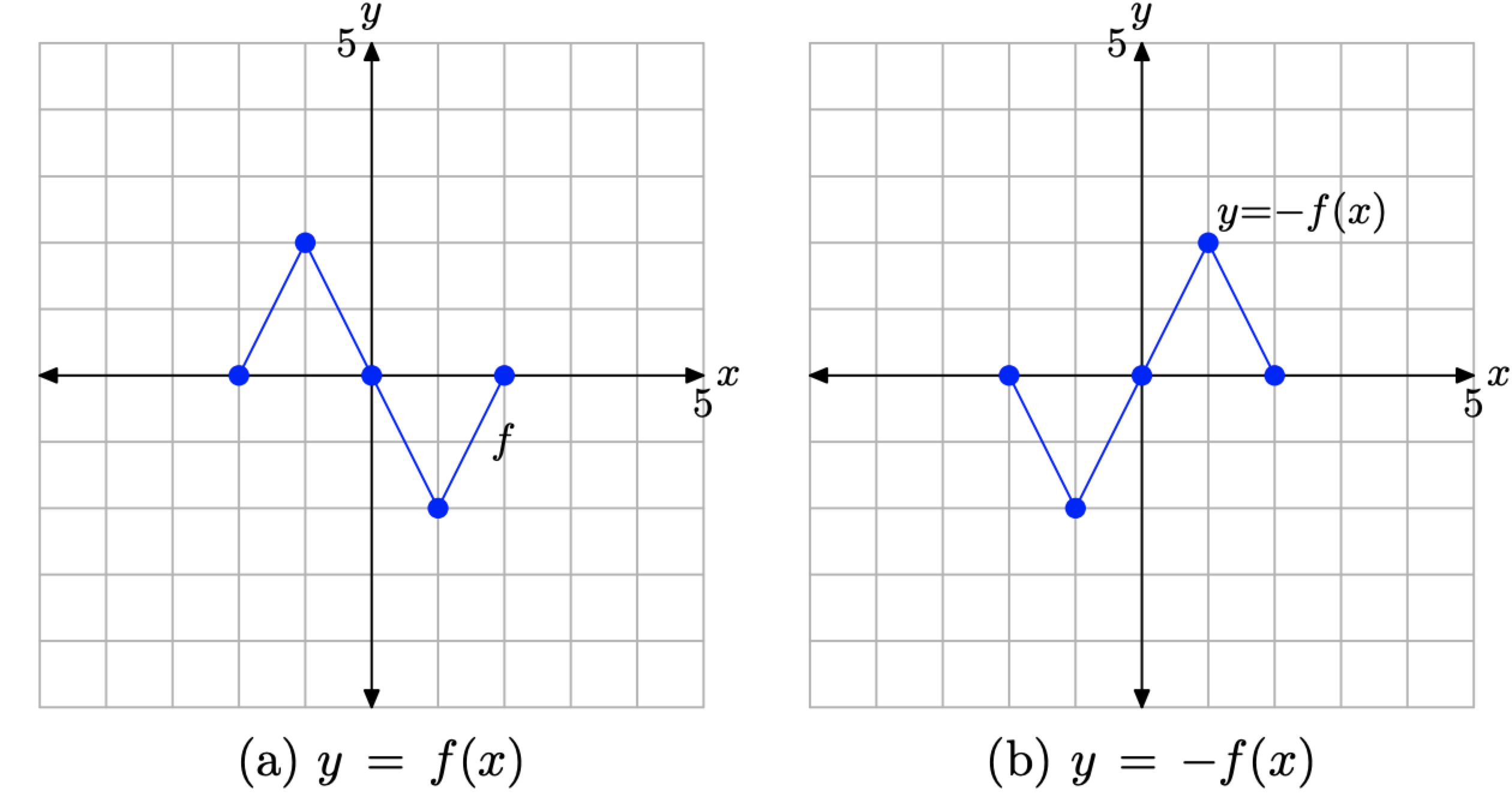
$WeChatf832c6332119614ecf42647cfe91a5c7.png$

Figura$\PageIndex{9}$. La gráfica de y = −f (x) es un reflejo de la gráfica de y = f (x) a través del eje x.

Así, dada la gráfica de y = f (x), es una tarea sencilla dibujar la gráfica de y = −f (x).

Para dibujar la gráfica de y = −f (x), toma cada punto de la gráfica de y = f (x) y reflejarla a través del eje x, manteniendo el valor x igual, pero negando el valor y.

Traducciones Verticales

Las traducciones son quizás la transformación más fácil de todas. Una traducción es un “cambio” o una “diapositiva”. Finge, por un momento, que has colocado una hoja transparente de plástico delgado sobre una hoja de papel cuadriculado. Has dibujado un sistema de coordenadas cartesianas en tu papel cuadriculado, pero has trazado tu gráfica en la lámina transparente de plástico. Ahora, “desplaza” o “desliza” la transparencia sobre tu papel cuadriculado en una dirección constante sin girar la transparencia. Esto es lo que queremos decir con una “traducción”. En esta sección, nos centraremos estrictamente en las traducciones verticales.

Por conveniencia, comenzamos repitiendo la gráfica original de y = f (x) y sus datos acompañantes en la Figura$\PageIndex{10}$ (a) y (b), respectivamente. Ahora traduciremos esta gráfica en la dirección vertical.

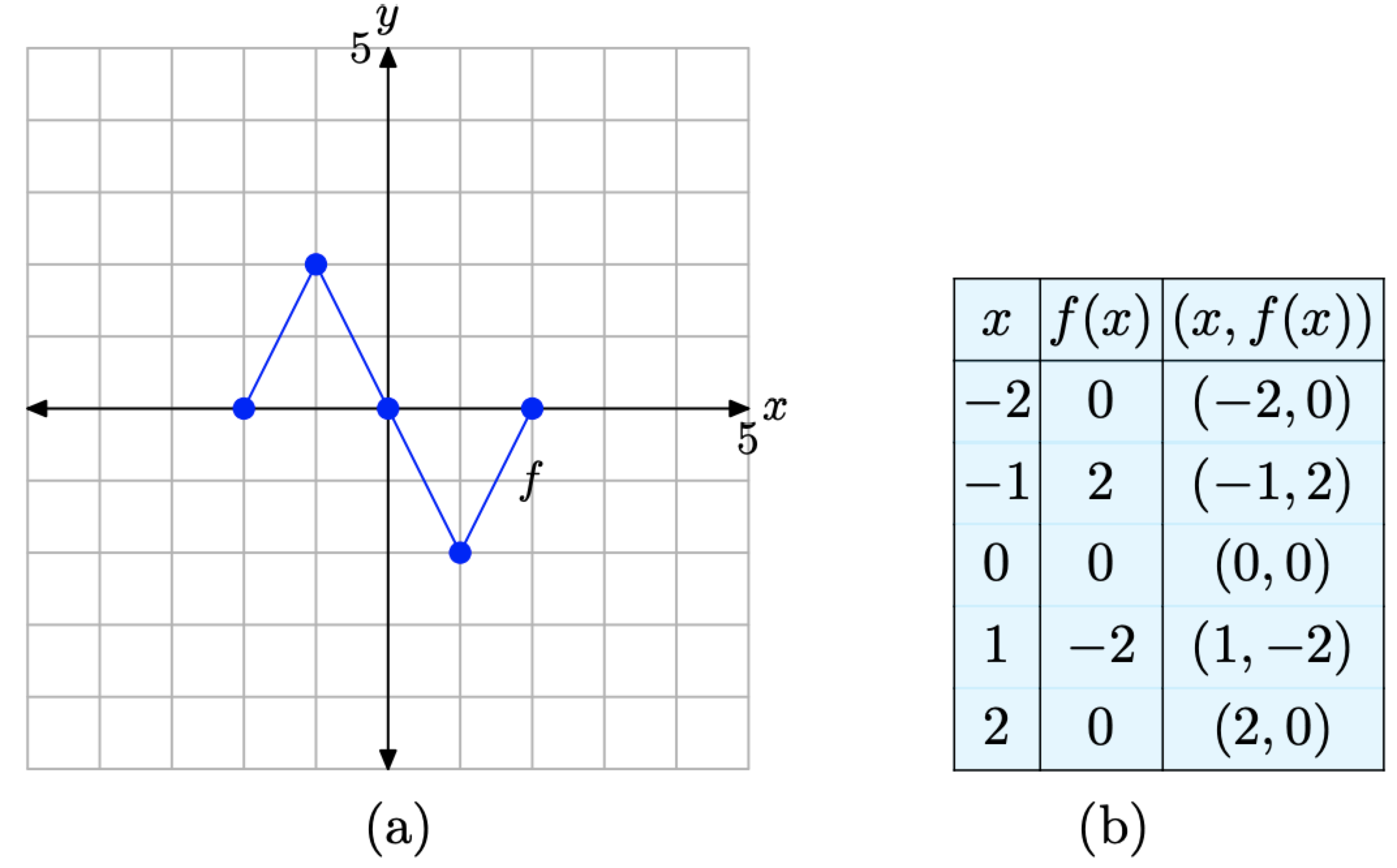
$WeChat18f468b011e27a8f2b0bc874ff92e6f2.png$

Figura$\PageIndex{10}$. La gráfica original de f y una tabla de puntos clave en la gráfica de f.

Ejemplo$\PageIndex{5}$

Si y = f (x) tiene la gráfica mostrada en la Figura$\PageIndex{10}$ (a), esboce la gráfica de y = f (x) + 1.

Solución

Evaluaremos y = f (x) +1 con los mismos valores que se muestran en la tabla de la Figura$\PageIndex{10}$ (b), es decir, x = −2, −1, 0, 1 y 2. Para evaluar y = f (x) +1 en el primer valor de x, concretamente x = −2, hacemos el siguiente cálculo\[y=f(-2)+1=0+1=1\]

donde hemos usado ese hecho de que f (−2) = 0 de la tabla en la Figura$\PageIndex{10}$ (b). De manera similar, podemos evaluar y = f (x) + 1 en cada uno de los valores restantes de x, es decir, x = −1, 0, 1 y 2.

\[\begin{array}{l}{y=f(-1)+1=2+1=3} \\ {y=f(0)+1=0+1=1} \\ {y=f(1)+1=-2+1=-1} \\ {y=f(2)+1=0+1=1}\end{array}\]

Ensamblamos estos puntos en la tabla de la Figura$\PageIndex{11}$ (b) y los trazamos en la Figura$\PageIndex{11}$ (a).

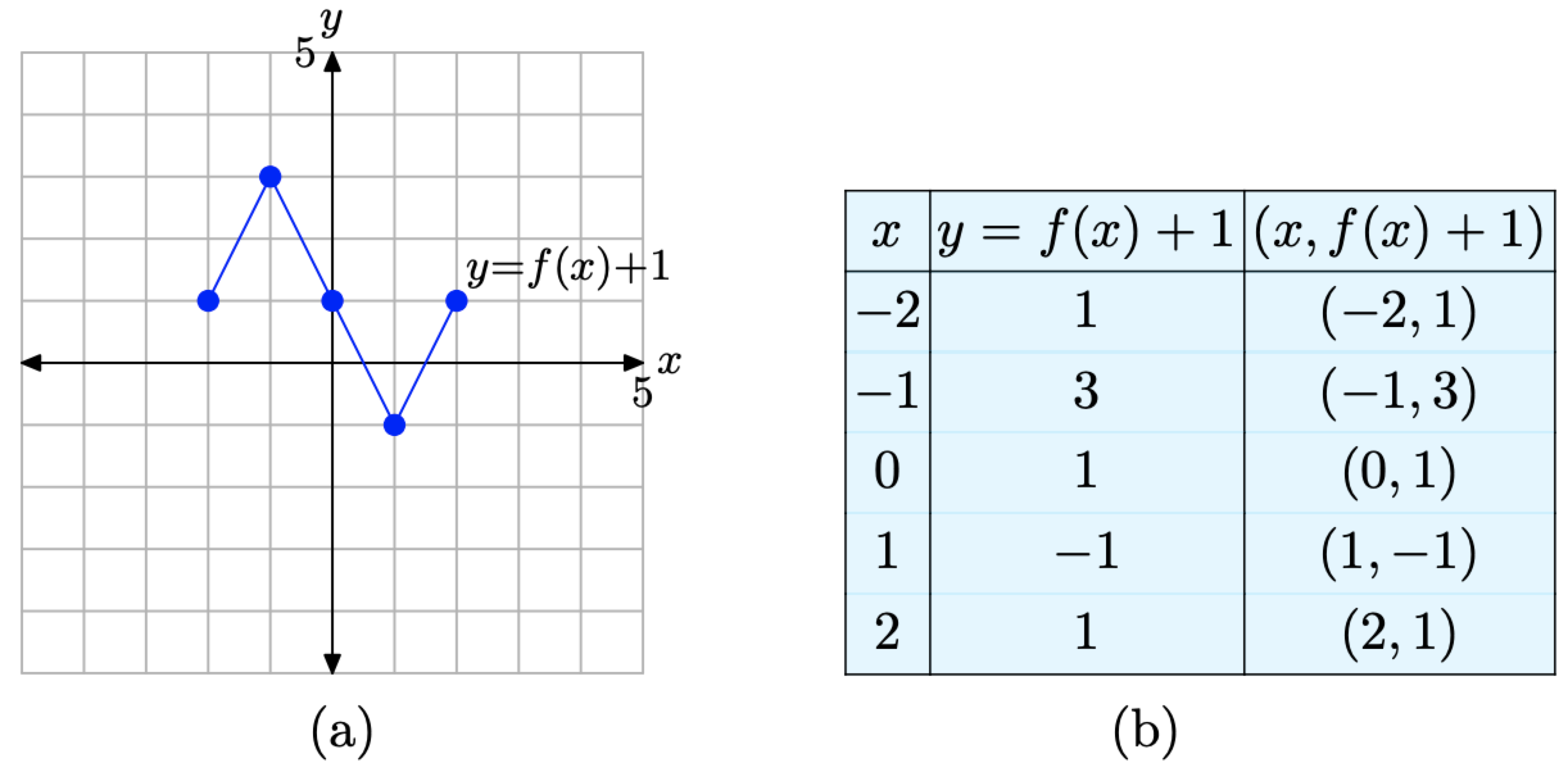
$WeChat1bcc53c1d90bf053fbdca96da5c88ac9.png$

Figura$\PageIndex{11}$. La gráfica de y = f (x) + 1 y una tabla de puntos clave en la gráfica.

Al comparar las entradas en la tabla de la Figura$\PageIndex{11}$. (b) con los valores originales en la tabla de la Figura$\PageIndex{10}$. (b), observará que los valores x en cada tabla son idénticos, pero los valores y en la tabla de la Figura$\PageIndex{11}$. b) se incrementan en 1. Esto tiene sentido, porque estos son los valores y de los puntos asociados a la función y = f (x) + 1. Por supuesto, todos los valores y deben ser 1 mayores que los valores y asociados con la ecuación original y = f (x).

Anote el resultado. La gráfica de y = f (x) + 1 en la Figura$\PageIndex{11}$ (a), cuando se compara con la gráfica de y = f (x) en la Figura$\PageIndex{10}$ (a), se desplaza 1 unidad hacia arriba.

Veamos otro ejemplo.

Ejemplo$\PageIndex{6}$

Si y = f (x) tiene la gráfica mostrada en la Figura$\PageIndex{10}$ (a), esboce la gráfica de y = f (x) − 2.

Solución

Evaluar la función y = f (x) − 2 en cada valor de x en la tabla de la Figura$\PageIndex{10}$ (b). En x = −2,\[y=f(-2)-2=0-2=-2\]

De manera similar, evalúe y = f (x) − 2 en cada valor x restante en la tabla de la Figura$\PageIndex{10}$ (b).

\[\begin{aligned} y &=f(-1)-2=2-2=0 \\ y &=f(0)-2=0-2=-2 \\ y &=f(1)-2=-2-2=-4 \\ y &=f(2)-2=0-2=-2 \end{aligned}\]

Ensamblamos estos puntos en la tabla de la Figura$\PageIndex{12}$ (b) y los trazamos en la Figura$\PageIndex{12}$ (a).

Al comparar las entradas de la tabla de la Figura$\PageIndex{12}$ (b) con los valores originales de la tabla de la Figura$\PageIndex{10}$ (b), notará que los valores x en cada tabla son idénticos, pero los valores y en la tabla de la Figura$\PageIndex{12}$ (b) están todos decrementados en 2. Esto hace

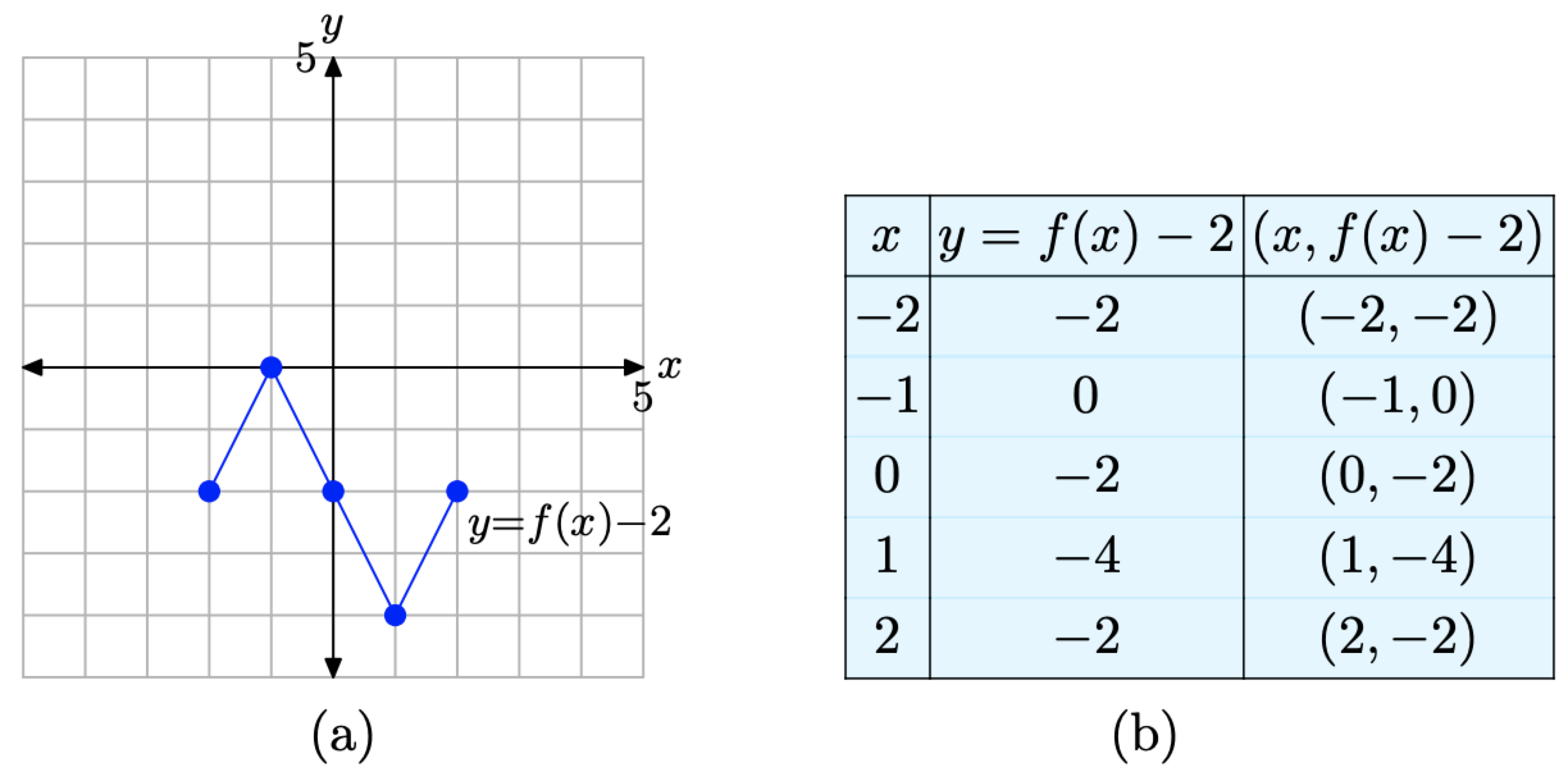
$WeChat3e19d071a3a0907d7ee21b7043eff748.png$

Figura$\PageIndex{12}$. La gráfica de y = f (x) − 2 y una tabla de puntos clave en la gráfica.

sense, porque estos son los valores y de los puntos asociados a la función y = f (x) − 2. Por supuesto, todos los valores y deben ser 2 menores que los valores y asociados con la ecuación original y = f (x).

Anote el resultado. La gráfica de y = f (x) − 2 en la Figura$\PageIndex{12}$ (a), cuando se compara con la gráfica de y = f (x) en la Figura$\PageIndex{10}$ (a), se desplaza hacia abajo 2 unidades.

Resumimos lo que hemos aprendido sobre las traducciones verticales.

Un Resumen Visual — Traducciones Verticales (Turnos)

Considera las imágenes en la Figura$\PageIndex{13}$.

En la Figura$\PageIndex{13}$ (a), vemos representado el gráfico de la función original y = f (x).
En la Figura$\PageIndex{13}$ (b), nótese que cada punto clave en la gráfica de y = f (x) + 1 tiene un valor y que es precisamente 1 unidad mayor que el valor y del punto correspondiente en la gráfica de y = f (x) en la Figura$\PageIndex{13}$ (a).
En la Figura$\PageIndex{13}$ (c), observe que cada punto clave en la gráfica de y = f (x) − 2 tiene un valor y que es precisamente 2 unidades menor que el valor y del punto correspondiente en la gráfica de y = f (x) en la Figura$\PageIndex{13}$ (a).
Tenga en cuenta que el valor x de cada punto transformado sigue siendo el mismo.

El resumen visual en Figura$\PageIndex{13}$ hace que bosquejar las gráficas de y = f (x) + 1 e y = f (x) − 2 sea una tarea fácil.

Dada la gráfica de y = f (x), para bosquejar la gráfica de y = f (x) + 1, simplemente tomar cada punto de la gráfica de y = f (x) y moverlo hacia arriba 1 unidad, manteniendo el mismo valor x.
Dada la gráfica de y = f (x), para bosquejar la gráfica de y = f (x) − 2, simplemente tomar cada punto de la gráfica de y = f (x) y moverlo hacia abajo 2 unidades, manteniendo el mismo valor x.

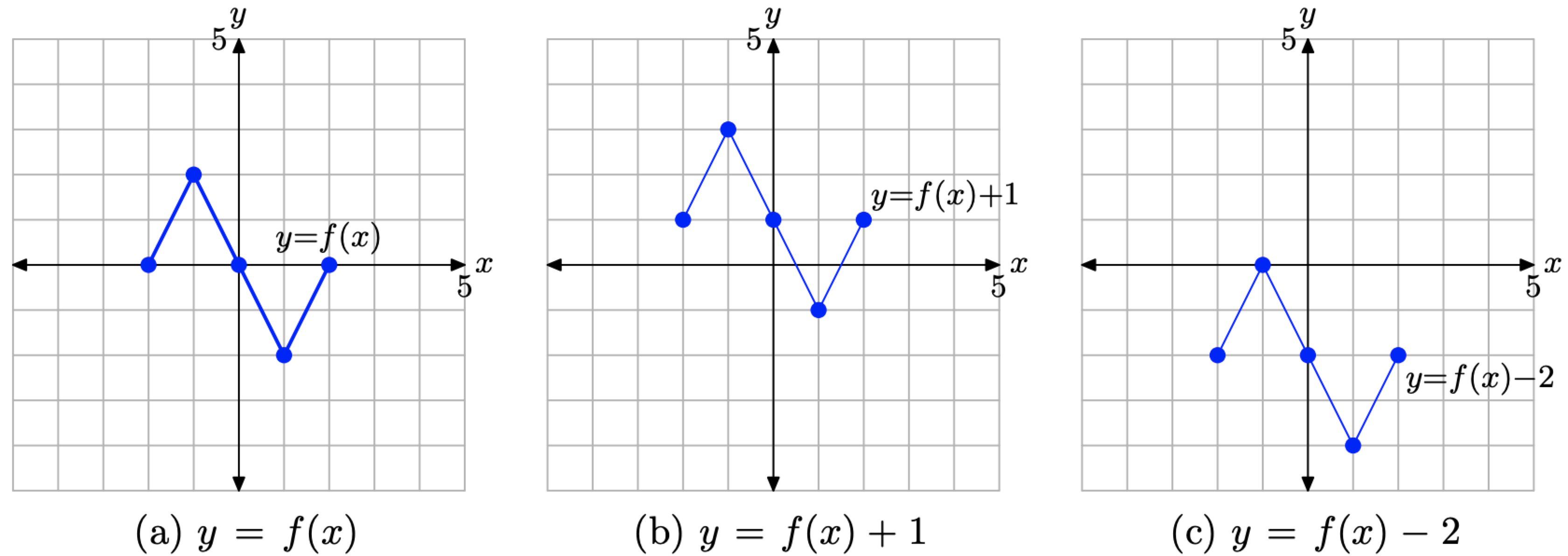
$WeChat20d85db2c4d982b69b890d936fa7cafa.png$

Figura$\PageIndex{13}$. La gráfica de y = f (x) + 1 se forma desplazando (verticalmente) la gráfica de y = f (x) hacia arriba 1 unidad. La gráfica de y = f (x) − 2 se forma desplazando (verticalmente) la gráfica de y = f (x) hacia abajo 2 unidades.

En general, podemos exponer lo siguiente.

resumen

Supongamos que se nos da la gráfica de y = f (x) y supongamos que c es cualquier número real positivo.

La gráfica de y = f (x) +c se desplaza c unidades hacia arriba de la gráfica de y = f (x).
La gráfica de y = f (x) − c se desplaza c unidades hacia abajo desde la gráfica de y = f (x).

Componiendo transformaciones

A veces vamos a querer realizar una transformación, luego tomar el resultado de la primera transformación y aplicar una segunda transformación. Veamos un ejemplo.

Ejemplo$\PageIndex{7}$

Considera la gráfica de y = f (x) presentada en la Figura$\PageIndex{14}$.

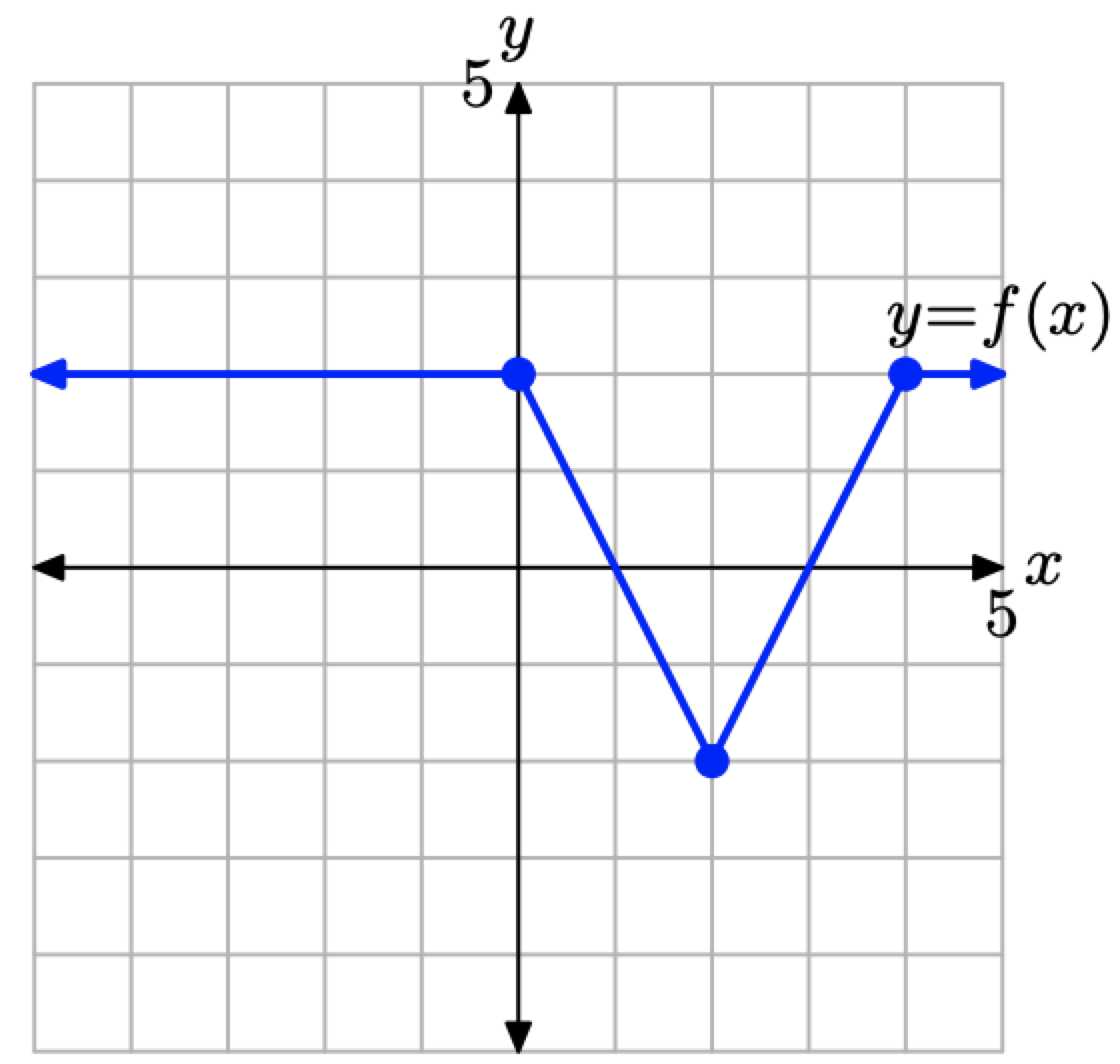
$WeChat937ead318813960d5bf0b08ccf94ade9.png$

Figura$\PageIndex{14}$ La gráfica de y = f (x) que se transformará en Ejemplo$\PageIndex{7}$.

Utilice los conceptos discutidos en los Resúmenes Visuales para esbozar la gráfica de y = −2f (x) sin crear y hacer referencia a una tabla de puntos.

Solución

Obsérvese que la ecuación y = −2f (x) puede estar formada por una secuencia de dos transformaciones.

Primero, escala la función original y = f (x) para obtener la ecuación y = 2f (x).
Segundo, niega la función resultante y = 2f (x) para obtener la ecuación y = −2f (x).

Así, la gráfica de y = −2f (x) se puede formar de la siguiente manera:

Comienza con la gráfica de y = f (x) y duplica el valor y de cada punto en la gráfica de y = f (x), manteniendo el mismo valor x. El resultado es la gráfica de y = 2f (x) que se muestra en la Figura$\PageIndex{15}$ (b).
A continuación, niega el valor y de cada punto en la gráfica de y = 2f (x), manteniendo el mismo valor x. El resultado es la gráfica de y = −2f (x) en la Figura$\PageIndex{15}$ (c).

$WeChat7c00a30968686057ddb449a6b65db15a.png$

Figura$\PageIndex{15}$. Transformar la gráfica de y = f (x) con una secuencia de dos transformaciones.

Es interesante señalar que obtendrá el mismo resultado si niega primero, luego escala el resultado. Dejaremos que nuestros lectores comprueben que esto es cierto.

Veamos un último ejemplo.

Ejemplo$\PageIndex{8}$

Considera la gráfica de y = f (x) presentada en la Figura$\PageIndex{16}$.

Utilice los conceptos discutidos en los Resúmenes Visuales para esbozar la gráfica de y = −f (x) +2 sin crear y hacer referencia a una tabla de puntos.

Solución

Obsérvese que la ecuación y = −f (x) + 2 puede estar formada por una secuencia de dos transformaciones.

Primero, niega la función original y = f (x) para obtener la ecuación y = −f (x).
Segundo, suma 2 a la función resultante y = −f (x) para obtener la ecuación y = −f (x) + 2.

Así, la gráfica de y = −f (x) + 2 se puede formar de la siguiente manera.

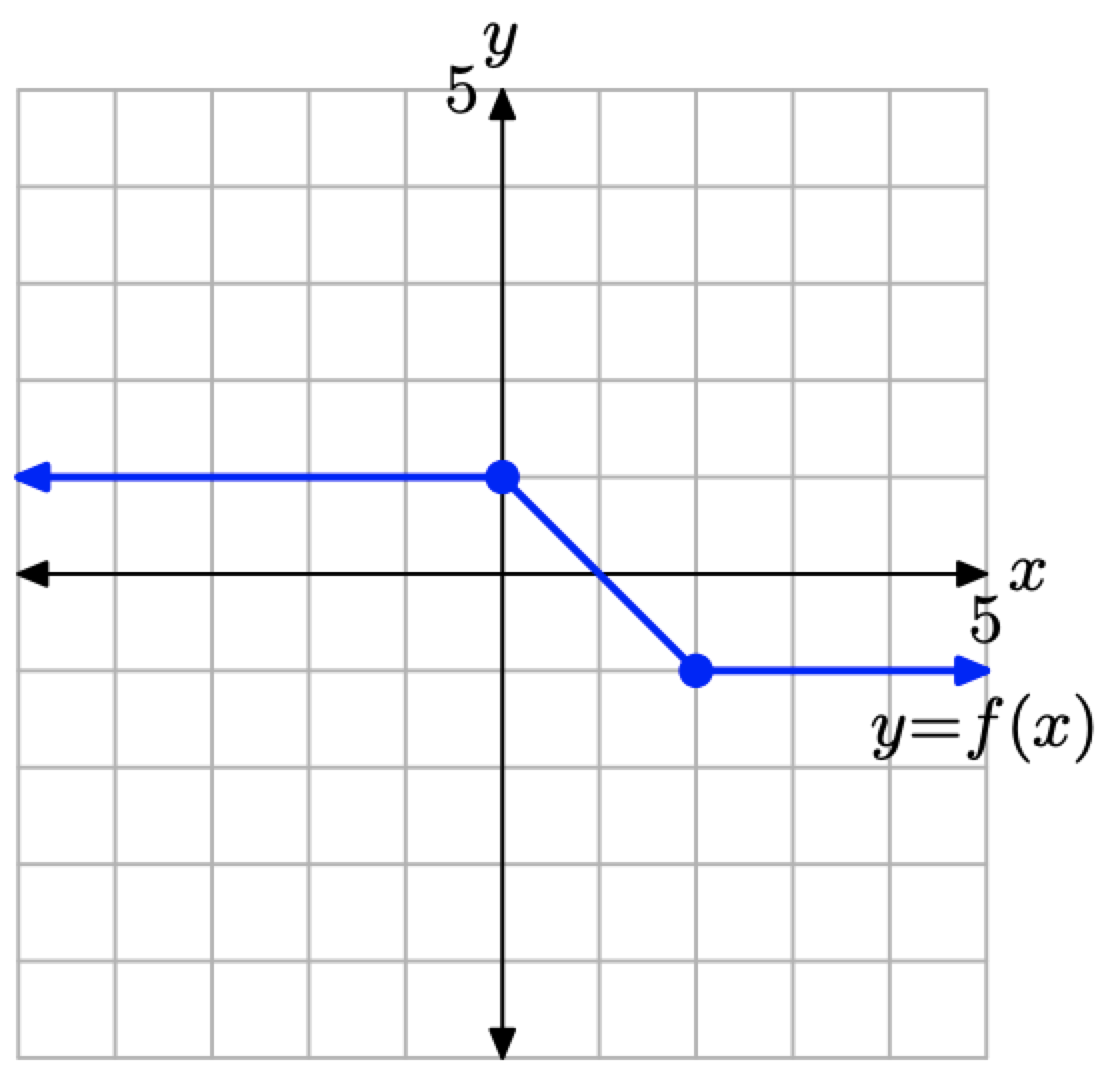
$WeChat6c4dcdb2dd6f7993faa7d1dc766c1bec.png$

Figura$\PageIndex{16}$. La gráfica de y = f (x) que se transformará en Ejemplo$\PageIndex{8}$.

1. Primero, comienza con la gráfica de y = f (x) en la Figura$\PageIndex{17}$ (a) y niega el valor y de cada punto para producir la gráfica de y = −f (x) Figura$\PageIndex{17}$ (b).

2. A continuación, agregue 2 al valor y de cada punto en la gráfica de y = −f (x) en la Figura$\PageIndex{17}$ (b) para producir la gráfica de y = −f (x) + 2 en la Figura$\PageIndex{17}$ (c).

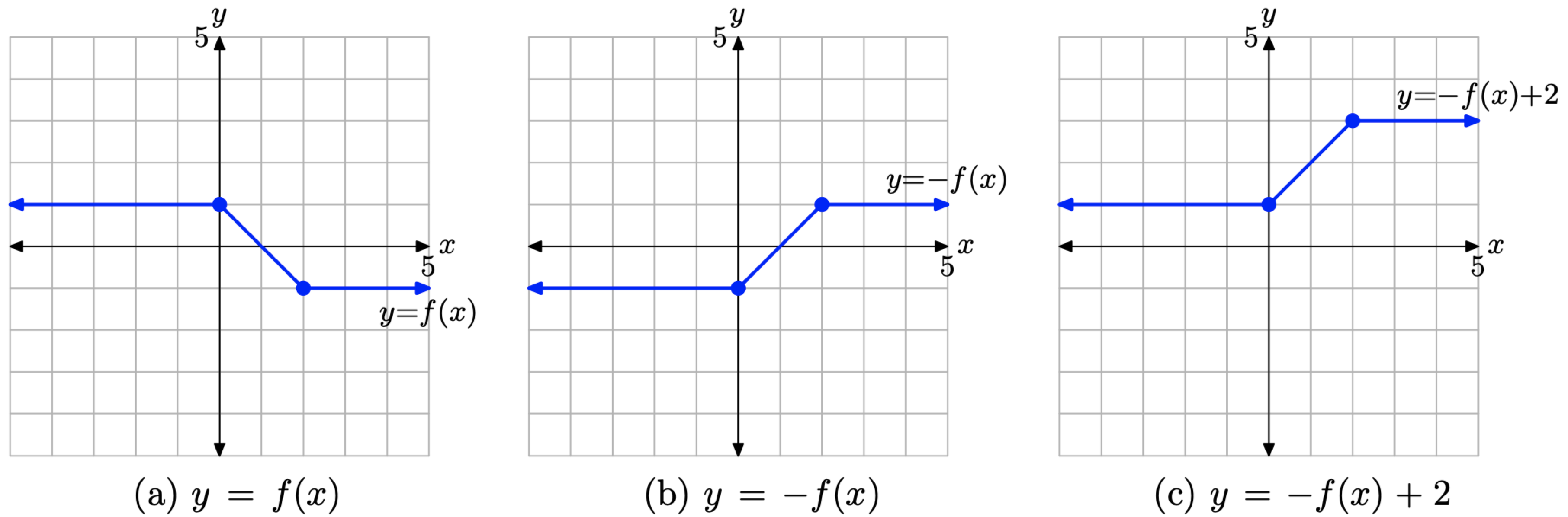
$WeChat890a4972b242609b51359f499af540fc.png$

Figura$\PageIndex{17}$. Transformar la gráfica de y = f (x), primero reflejando a través del eje x, luego desplazando 2 unidades hacia arriba para obtener la gráfica de y = −f (x) + 2.

En Ejemplo$\PageIndex{7}$, donde empezamos con la gráfica de y = f (x) y luego graficamos y = 2f (x), el orden de las transformaciones no importaba. Escala por 2, luego niega, o niega y escala por 2, obtienes el mismo resultado (los lectores deben verificar esta afirmación). Sin embargo, en este ejemplo, el orden en que se aplican las transformaciones sí importa. Para ver esto, hagamos lo siguiente:

Sumar 2 para desplazar la gráfica de y = f (x) en la Figura$\PageIndex{18}$ (a) dos unidades hacia arriba para obtener la gráfica de y = f (x) + 2 en la Figura$\PageIndex{18}$ (b).
Nega el valor y de cada punto en la gráfica de y = f (x) + 2 en la Figura$\PageIndex{18}$ (b) para obtener la gráfica de y = − (f (x) + 2) en la Figura$\PageIndex{18}$ (c). Tenga en cuenta que debemos negar todo el valor y. De ahí los paréntesis.

Desafortunadamente, la gráfica de y = − (f (x) + 2) en la Figura$\PageIndex{18}$ (c) no es la misma que la gráfica de y = −f (x) + 2 en la Figura$\PageIndex{17}$ (c). Pero claro, esto tiene sentido completo, ya que las ecuaciones (en el caso de la Figura$\PageIndex{18}$ (c))

\[y=-(f(x)+2)=-f(x)-2\]

y (en el caso de la Figura$\PageIndex{17}$ c))

\[y=-f(x)+2\]

tampoco son lo mismo.

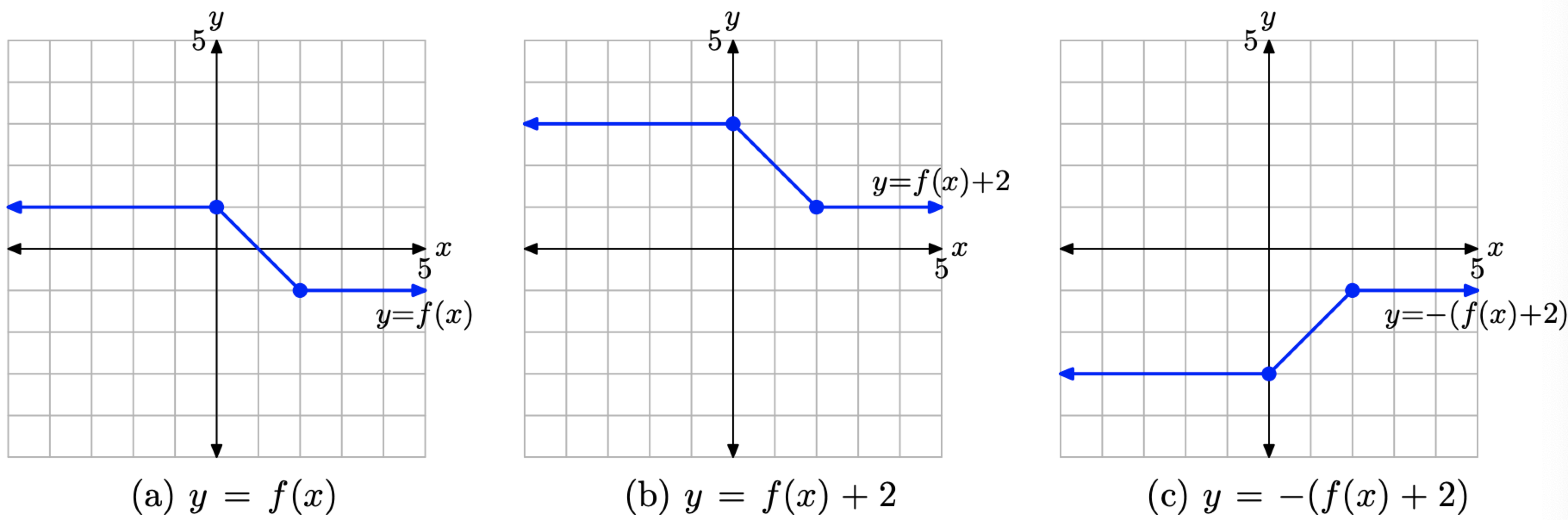
$WeChatbf6ad2cde0793cd167583aec2ba44f13.png$

Figura$\PageIndex{18}$. Transformando la gráfica de y = f (x), desplazando 2 unidades hacia arriba para obtener la gráfica de y = f (x) + 2, luego reflejando a través del eje x para obtener la gráfica de y = − (f (x) + 2).

Por lo tanto, se debe tener cuidado al aplicar más de una transformación. Aquí hay una buena regla general para vivir.

Haga Escalamientos Verticales y Reflexiones Primero, luego Traducciones Verticales. Al realizar una secuencia de transformaciones verticales, suele ser más fácil (menos confuso) aplicar escalados verticales y reflejos antes de las traducciones verticales.

No obstante, siempre y cuando realices las transformaciones correctamente, debes obtener el resultado correcto. En Ejemplo$\PageIndex{8}$, si quieres bosquejar la gráfica de y = −f (x) +2 haciendo primero la traducción, la forma correcta de proceder es la siguiente (aunque algo contraintuitiva):

Primero, desplaza la gráfica de y = f (x) hacia abajo 2 unidades para obtener la gráfica de y = f (x) − 2.
Segundo, reflejar la gráfica de y = f (x) − 2 a través del eje x para obtener la gráfica de y = − (f (x) − 2). Nuevamente, tenga en cuenta el uso de paréntesis ya que negamos todo el valor y.

Por último, tenga en cuenta que\[y=-(f(x)-2)=-f(x)+2\]

Dejaremos a nuestros lectores demostrar que esta secuencia produce el resultado correcto, una gráfica idéntica a la respuesta correcta mostrada en la Figura$\PageIndex{17}$ (c).

Resumen

En esta sección hemos visto cómo un puñado de transformaciones mejoran enormemente nuestra capacidad de graficar. Terminamos esta sección enumerando las transformaciones que se presentan en esta sección y sus efectos en la gráfica de una función.

Transformaciones Verticales.

Transformaciones Verticales. Supongamos que se nos da la gráfica de y = f (x).

Si$a > 1$, entonces la gráfica de y = af (x) se estira verticalmente (alejándose del eje x), tanto positiva como negativamente, por un factor de a.
Si$0 < a < 1$, entonces la gráfica de y = af (x) se comprime verticalmente (hacia el eje x), tanto positiva como negativamente, por un factor de 1/a.
La gráfica de y = −f (x) es un reflejo de la gráfica de y = f (x) a través del eje x.
Si$c > 0$, entonces la gráfica de y = f (x) + c se desplaza c unidades hacia arriba desde la gráfica de y = f (x).
Si$c > 0$, entonces la gráfica de y = f (x) − c se desplaza c unidades hacia abajo desde la gráfica de y = f (x).

Search

Text Color

Text Size

Margin Size

Font Type