5.6: Optimización
- Page ID
- 110745
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección exploraremos la ciencia de la optimización. Supongamos que está tratando de encontrar un par de números con una suma fija para que el producto de los dos números sea un máximo. Este es un ejemplo de un problema de optimización. Sin embargo, la optimización no se limita a encontrar un máximo. Por ejemplo, consideremos al fabricante que quisiera minimizar sus costos con base en ciertos criterios. Este es otro ejemplo de un problema de optimización. Como puede ver, la optimización puede abarcar encontrar ya sea un máximo o un mínimo.
La optimización se puede aplicar a una amplia familia de diferentes funciones. Sin embargo, en esta sección, nos concentraremos en encontrar los máximos y mínimos de las funciones cuadráticas. Existe un gran cuerpo de aplicaciones de la vida real que pueden modelarse mediante funciones cuadráticas, por lo que encontraremos que este es un excelente punto de entrada al estudio de la optimización.
Encontrar el Máximo o Mínimo de una Función Cuadrática
Considerar la función cuadrática
\[f(x)=-x^{2}+4 x+2 \nonumber\]
Completemos el cuadrado para colocar esta función cuadrática en forma de vértice. Primero, factorial un signo menos.
\[f(x)=-\left[x^{2}-4 x-2\right] \nonumber\]
Tomar la mitad del coeficiente de\(x\) y cuadrado, como en\([(1 / 2)(-4)]^{2}=4\). Sumar y restar esta cantidad para mantener equilibrada la ecuación.
\[f(x)=-\left[x^{2}-4 x+4-4-2\right] \nonumber\]
Factorizar el trinomio cuadrado perfecto, combinar las constantes al final y luego redistribuir el signo menos para colocar la función cuadrática en forma de vértice.
\[\begin{array}{l}{f(x)=-\left[(x-2)^{2}-6\right]} \\ {f(x)=-(x-2)^{2}+6}\end{array} \nonumber\]
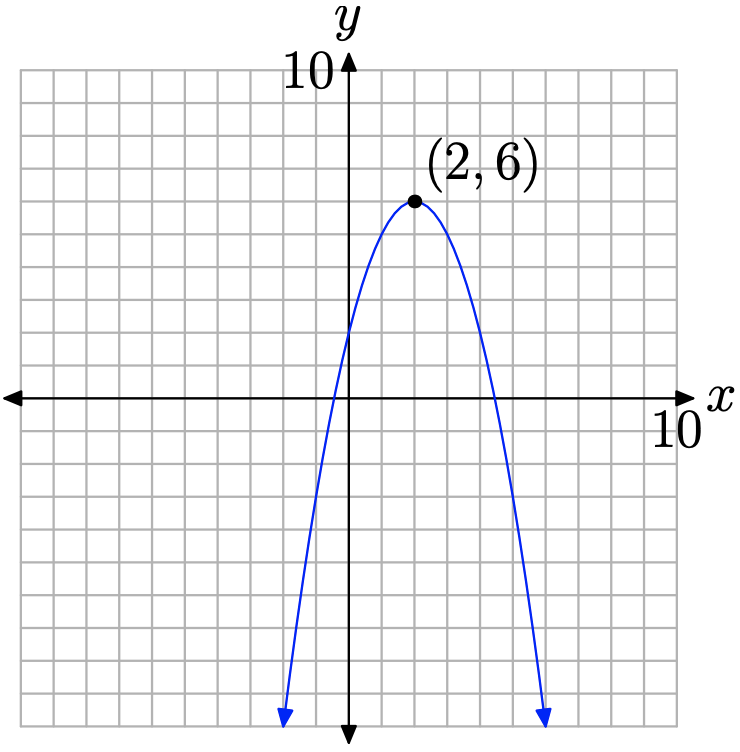
Se trata de una parábola que se abre hacia abajo, se ha desplazado 2 unidades a la derecha y 6 unidades hacia arriba. Esto coloca el vértice de la parábola en (2, 6), como se muestra en la Figura 1. Tenga en cuenta que el valor máximo de la función (valor y) ocurre en el vértice de la parábola. Un matemático diría que la función “alcanza un valor máximo de 6 a\(x\) igual a 2”.
Tenga en cuenta que 6 es mayor o igual a cualquier otro valor y (valor de función) que ocurra en la parábola. Esto da lugar a la siguiente definición.
Definición: Maximum
Seamos\(c\) en el dominio de\(f\). \(f\)Se dice que la función alcanza un máximo en\(x=c\) si\(f(c) \geq f(x)\) para todos\(x\) en el dominio de\(f\).
A continuación, veamos una función cuadrática que alcanza un mínimo en su dominio.
Ejemplo\(\PageIndex{1}\)
A continuación, veamos una función cuadrática que alcanza un mínimo en su dominio.
\[f(x)=2 x^{2}+12 x+12\]
Solución
Factorar un 2. \[f(x)=2\left[x^{2}+6 x+6\right]\]
Tomar la mitad del coeficiente de x y cuadrado, como en\([(1 / 2)(6)]^{2}=9\). Sumar y restar esta cantidad para mantener equilibrada la ecuación.
\[f(x)=2\left[x^{2}+6 x+9-9+6\right]\]
Factorizar el trinomio y combinar las constantes, para luego redistribuir el 2 en el siguiente paso.
\[\begin{array}{l}{f(x)=2\left[(x+3)^{2}-3\right]} \\ {f(x)=2(x+3)^{2}-6}\end{array}\]
El gráfico es una parábola que se abre hacia arriba, desplazada 3 unidades hacia la izquierda y 6 unidades hacia abajo. Esto coloca el vértice en (−3, −6), como se muestra en la Figura\(\PageIndex{2}\). Tenga en cuenta que el valor mínimo de la función (valor y) ocurre en el vértice de la parábola. Un matemático diría que la función “alcanza un valor mínimo de −6 en x es igual a −3.
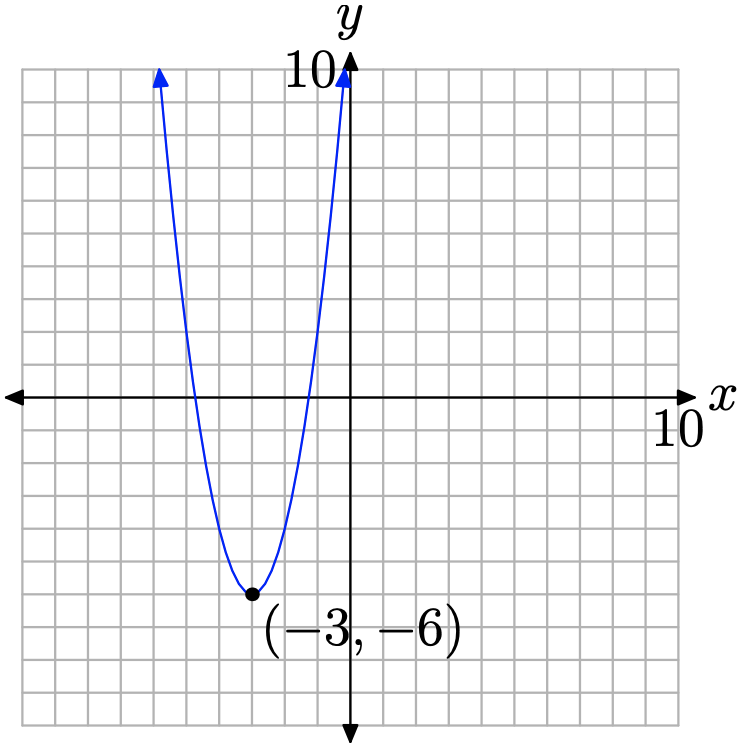
Tenga en cuenta que −6 es menor o igual a cualquier otro valor y (valor de función) que ocurra en la parábola.
Este último ejemplo da lugar a la siguiente definición.
Definición
Sea c en el dominio de f. Se dice que la función f logra un mínimo en x = c si\(f(c) \leq f(x)\) para todo x en el dominio de f.
Un atajo para el vértice
Ahora debería quedar claro que el vértice de la parábola juega un papel crucial a la hora de optimizar una función cuadrática. También sabemos que podemos completar el cuadrado para encontrar las coordenadas del vértice. No obstante, sería bueno que tuviéramos una forma más rápida de encontrar las coordenadas del vértice. Veamos la función cuadrática general
\[y=a x^{2}+b x+c\]
y completar el cuadrado para encontrar las coordenadas del vértice. En primer lugar, factifique la a.
\[y=a\left[x^{2}+\frac{b}{a} x+\frac{c}{a}\right]\]
Tomar la mitad del coeficiente de x y cuadrado, como en\([(1 / 2)(b / a)]^{2}=[b /(2 a)]^{2}=b^{2} /\left(4 a^{2}\right)\). Sumar y restar esta cantidad para mantener equilibrada la ecuación.
\[y=a\left[x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}-\frac{b^{2}}{4 a^{2}}+\frac{c}{a}\right]\]
Factorizar el trinomio cuadrado perfecto y hacer fracciones equivalentes para los términos constantes con un denominador común.
\[\begin{array}{l}{y=a\left[\left(x+\frac{b}{2 a}\right)^{2}-\frac{b^{2}}{4 a^{2}}+\frac{4 a c}{4 a^{2}}\right]} \\ {y=a\left[\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a^{2}}\right]}\end{array}\]
Por último, redistribuya que a. Obsérvese cómo multiplicar por un cancela uno a en el denominador del término constante.
\[y=a\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a}\]
Ahora, aquí está la idea clave. Los resultados dependen de los valores de a, b y c, pero debe quedar claro que las coordenadas del vértice son
\[\left(-\frac{b}{2 a}, \frac{4 a c-b^{2}}{4 a}\right)\]
El valor y del vértice es un poco difícil de memorizar, pero el valor x del vértice es fácil de memorizar.
Acceso directo a vértices
Dada la parábola representada por la función cuadrática\[y=a x^{2}+b x+c\]
la coordenada x del vértice viene dada por la fórmula\[x_{\text { vertex }}=-\frac{b}{2 a}\]
Probemos esto con la función cuadrática dada en Ejemplo\(\PageIndex{1}\).
Ejemplo\(\PageIndex{2}\)
Usa la fórmula\(x_{\text { vertex }}=-b /(2 a)\) para encontrar la coordenada x del vértice de la parábola representada por la función cuadrática en Ejemplo\(\PageIndex{1}\).
Solución
En Ejemplo\(\PageIndex{1}\), la función cuadrática fue representada por la ecuación\[f(x)=2 x^{2}+12 x+12\]
En forma de vértice\[f(x)=2(x+3)^{2}-6\]
las coordenadas del vértice se vieron fácilmente como (−3, −6) (ver Figura\(\PageIndex{2}\)). Veamos qué revela la nueva fórmula para la coordenada x del vértice.
Como es habitual, compare\(f(x)=2 x^{2}+12 x+12\) con\(f(x)=a x^{2}+b x+c\) y anote que a = 2, b = 12 y c = 12. Así, la coordenada x del vértice viene dada por
\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{12}{2(2)}=-3\]
Obsérvese que esto concuerda con el resultado anterior (ver Figura\(\PageIndex{2}\)). Podríamos encontrar la coordenada y del vértice con
\[y_{\text { vertex }}=\frac{4 a c-b^{2}}{4 a}=\frac{4(2)(12)-(12)^{2}}{4(2)}=\frac{-48}{8}=-6\]
pero encontramos esta fórmula para la coordenada y del vértice un poco difícil de memorizar. Nos resulta más fácil hacer lo siguiente. Como sabemos que la coordenada x del vértice es x = −3, podemos encontrar la coordenada y del vértice simplemente sustituyendo x = −3 en la ecuación de la parábola. Es decir, con\(f(x)=2 x^{2}+12 x-12\),
\[f(-3)=2(-3)^{2}+12(-3)+12=-6\]
Destacemos esta última técnica.
Encontrar la coordenada y del vértice
Dada la parábola representada por la función cuadrática\[f(x)=a x^{2}+b x+c\]
hemos visto que la coordenada x del vértice viene dada por x = −b/ (2a). Para encontrar la coordenada y del vértice, probablemente sea más fácil evaluar la función en x = −b/ (2a). Es decir, la coordenada y del vértice viene dada por
\[y_{\text { vertex }}=f\left(-\frac{b}{2 a}\right)\]
Veamos otro ejemplo.
Ejemplo\(\PageIndex{3}\)
Considera que la parábola tiene ecuación\[f(x)=-2 x^{2}+3 x-8\]
Encuentra las coordenadas del vértice.
Solución
Primero, usa la nueva fórmula para encontrar la coordenada x del vértice.
\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{3}{2(-2)}=\frac{3}{4}\]
A continuación, sustituya x = 3/4 para encontrar la coordenada y correspondiente.
\[\begin{aligned} f\left(\frac{3}{4}\right) &=-2\left(\frac{3}{4}\right)^{2}+3\left(\frac{3}{4}\right)-8 \\ &=-2\left(\frac{9}{16}\right)+\frac{9}{4}-8 \\ &=-\frac{9}{8}+\frac{18}{8}-\frac{64}{8} \\ &=-\frac{55}{8} \end{aligned}\]
Así, las coordenadas del vértice son (3/4, −55/8).
Aplicaciones
Ahora estamos en condiciones de hacer algunas aplicaciones de optimización. Empecemos con un ejemplo fácil.
Ejemplo\(\PageIndex{4}\)
Encuentra dos números reales x e y que sumen a 50 y que tengan un producto que sea máximo.
Solución
Antes de aplicar la teoría de los ejemplos anteriores, juguemos un poco con los números para tener una idea de lo que se nos pide que hagamos. Necesitamos encontrar dos números que sumen a 50, así que comencemos con x = 5 e y = 45. Claramente, la suma de estos dos números es 50. Por otro lado, su producto es xy = (5) (45) = 225. Coloquemos este resultado en una tabla.
| x | y | xy |
|---|---|---|
| 5 | 45 | 225 |
Para una segunda conjetura, seleccione x = 10 e y = 40. La suma de estos dos números es 50 y su producto es xy = 400. Para una tercera suposición, seleccione x = 20 e y = 30. La suma de estos dos números es 50 y su producto es xy = 600. Agreguemos estos resultados a nuestra tabla.
| x | y | xy |
|---|---|---|
| 5 | 45 | 225 |
| 10 | 40 | 400 |
| 20 | 30 | 600 |
Hasta el momento, el mejor par es x = 20 e y = 30, debido a que su producto es el máximo en la tabla anterior. Pero ¿hay otro par con un producto más grande? Recuerda que nuestro objetivo es encontrar un par con un producto que sea máximo. Es decir, nuestro par debe tener un producto más grande que cualquier otro par. ¿Puedes encontrar un par que tenga un producto mayor a 600?
Ahora que tenemos una idea de lo que se nos pide que hagamos (encontrar dos números que sumen a 50 y que tengan un producto que sea máximo), probemos un enfoque que sea más abstracto que el enfoque de “adivinar y verificar” de nuestras tablas. Nuestra primera restricción es el hecho de que la suma de los números x e y debe ser 50. Podemos modelar esta restricción con la ecuación
\[x+y=50\]
Se nos pide que maximicemos el producto. Por lo tanto, desea encontrar una fórmula para el producto. Dejemos que P represente el producto de x e y y escriba
\[P=x y\]
Tenga en cuenta que P es una función de dos variables x e y, sin embargo, todas nuestras funciones en este curso han sido hasta ahora una función de una sola variable. Entonces, ¿cómo podemos deshacernos de una de las variables? Simple, primer resolver la ecuación (8) para y.
\[\begin{aligned} x+y &=50 \\ y &=50-x \end{aligned}\]
Ahora, sustituya la ecuación (10) en el producto en la ecuación (9).
\[P=x(50-x)\]
o, equivalentemente,
\[P=-x^{2}+50 x\]
Obsérvese que P es ahora una función de una sola variable x. Obsérvese además que la función definida por la ecuación (11) es cuadrática. Si comparamos\(P=-x^{2}+50 x\) con la forma general\(P=a x^{2}+b x+c\), anotar que a = −1 y b = 50 (no tenemos necesidad del hecho de que c = 0). Por lo tanto, si trazamos P versus x, la gráfica es una parábola que se abre hacia abajo (ver Figura\(\PageIndex{3}\)) y el valor máximo de P ocurrirá en el vértice. La coordenada x del vértice se encuentra con
\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{50}{2(-1)}=25\]
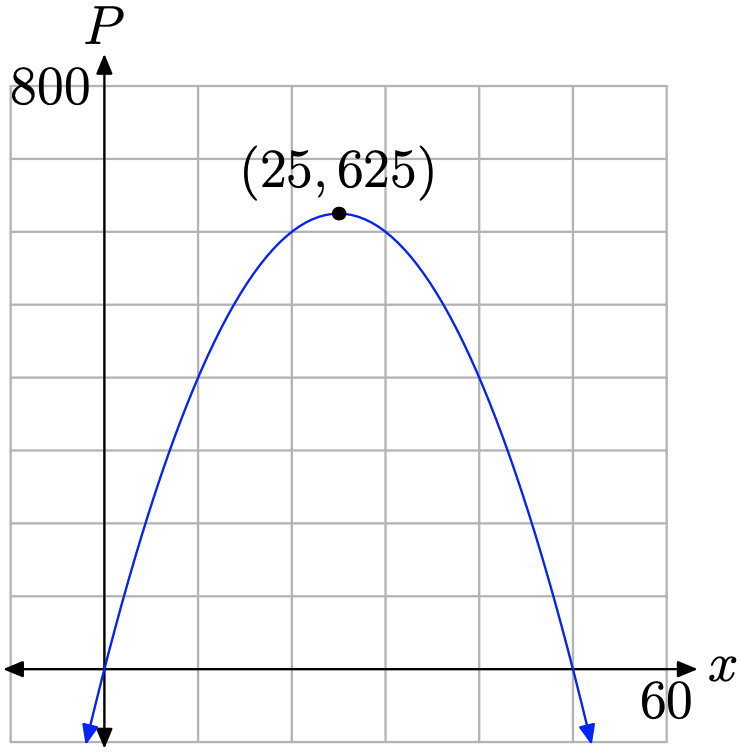
Así, nuestro primer número es x = 25. Podemos encontrar el segundo número y sustituyendo x = 25 en la ecuación (10).
\[y=50-x=50-25=25\]
Obsérvese que la suma de x e y es x + y = 25 + 25 = 50. Hay dos formas en las que podemos encontrar su producto. Como ahora conocemos los números x e y, podemos multiplicar para encontrar P = xy = (25) (25) = 625. Alternativamente, podríamos sustituir x = 25 en la ecuación (11) para obtener
\[P=-x^{2}+50 x=-(25)^{2}+50(25)=-625+1250=625\]
Cuando comparas este resultado con nuestras tablas experimentales, las cosas se juntan. Hemos encontrado dos números x e y que suman 50 con un producto que es máximo. Ningún otro número que sume 50 tiene un producto mayor.
Nuestra pequeña fórmula\(x_{\text { vertex }}=-b /(2 a)\) ha demostrado ser un poderoso aliado. Probemos otro ejemplo.
Ejemplo\(\PageIndex{5}\)
Encuentra dos números reales con una diferencia de 8 de tal manera que la suma de los cuadrados de los dos números sea mínima.
Solución
Empecemos por dejar que x e y representen los números que buscamos. A continuación, juguemos un poco como hicimos en el ejemplo anterior. Prueba x = 9 e y = 1. La diferencia de estos dos números es sin duda 8. La suma de los cuadrados de estos dos números es\(S=9^{2}+1^{2}=82\). Pongamos este resultado en forma tabular.
| x | y | \(S=x^{2}+y^{2}\) |
|---|---|---|
| 9 | 1 | \ (s=x^ {2} +y^ {2}\) ">82 |
Para una segunda conjetura, seleccione x = 8 e y = 0. La diferencia es x − y = 8 − 0 = 8, pero esta vez la suma de los cuadrados es\(S=8^{2}+0^{2}=64\). Para una tercera conjetura, prueba x = 7 e y = −1. Nuevamente, la diferencia es x − y = 7 − (−1) = 8, pero la suma de los cuadrados es ahora\(S=7^{2}+(-1)^{2}=50\). Agreguemos estos resultados a nuestra tabla.
| x | y | \(S=x^{2}+y^{2}\) |
|---|---|---|
| 9 | 1 | \ (s=x^ {2} +y^ {2}\) ">82 |
| 8 | 0 | \ (s=x^ {2} +y^ {2}\) ">64 |
| 7 | -1 | \ (s=x^ {2} +y^ {2}\) ">50 |
Hasta el momento, el par que minimiza la suma de los cuadrados es x = 7 e y = −1. No obstante, ¿podría haber otro par con una diferencia de 8 y la suma de los cuadrados es menor a 50? Experimenta más para ver si puedes mejor el mínimo actual de 50.
Probemos un enfoque analítico. Nuestra primera restricción es el hecho de que la diferencia de los dos números debe ser igual a 8. Esto se expresa fácilmente como
\[x-y=8\]
A continuación, se nos pide minimizar la suma de los cuadrados de los dos números. Esto requiere que encontremos una fórmula para la suma de los cuadrados. Que S represente la suma de los cuadrados de x e y. Así,
\[S=x^{2}+y^{2}\]
Tenga en cuenta que S es una función de dos variables. Podemos eliminar una de las variables resolviendo la ecuación (13) para x,\[x=y+8\]
luego sustituyendo este resultado en la ecuación (14).
\[S=(y+8)^{2}+y^{2}\]
Amplíe y simplifique. \[S=2 y^{2}+16 y+64\]
Compare\(S=2 y^{2}+16 y+64\) con la cuadrática general\(S=a y^{2}+b y+c\) y observe que a = 2 y b = 16. Así, la gráfica de S versus y será una parábola que se abre hacia arriba (ver Figura\(\PageIndex{4}\)) y el valor mínimo de S ocurrirá en el vértice. La coordenada y del vértice se encuentra con
\[y_{\mathrm{vertex}}=-\frac{b}{2 a}=-\frac{16}{2(2)}=-4\]
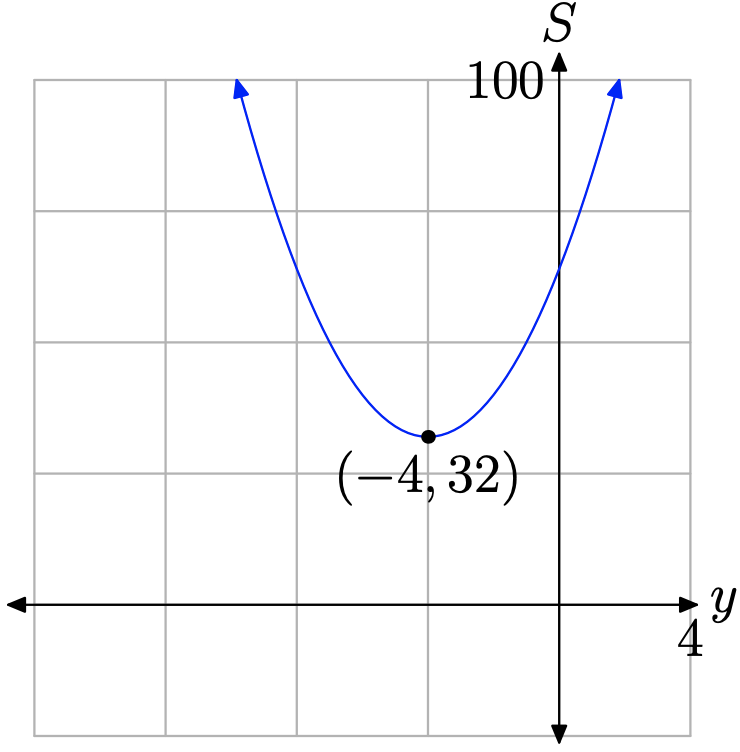
Así, el primer número que buscamos es y = −4. Podemos encontrar el segundo número sustituyendo y = −4 en la ecuación (15).
\[x=y+8=(-4)+8=4\]
De ahí que los números que buscamos son x = 4 e y = −4. Obsérvese que la diferencia de estos dos números es x−y = 4− (−4) = 8 y la suma de sus cuadrados es\(S=(4)^{2}+(-4)^{2}=32\), que es menor que el mejor resultado encontrado en nuestro experimento tabular anterior. En efecto, nuestro trabajo demuestra que este es el valor más pequeño posible de S.
Alternativamente, puede encontrar S sustituyendo y = −4 en la ecuación (16). Dejaremos que nuestros lectores verifiquen que esto también da un valor mínimo de S = 32.
Veamos otra aplicación.
Ejemplo\(\PageIndex{6}\)
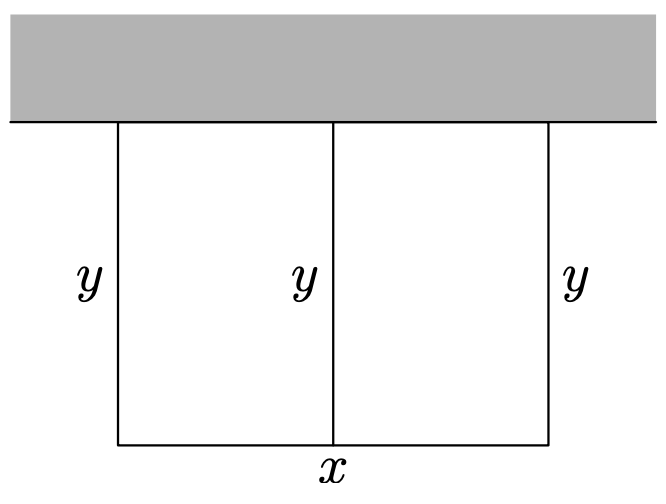
María quiere cercar un jardín rectangular para evitar que el venado coma sus frutas y verduras. Un lado de su jardín colinda con la pared de su cobertizo así que no necesitará cercar ese lado. No obstante, también quiere utilizar material para separar el jardín rectangular en dos secciones (ver Figura\(\PageIndex{5}\)). Ella puede darse el lujo de comprar 80 pies totales de cercado para usar para el perímetro y la sección que divide el jardín rectangular. ¿Qué dimensiones maximizarán el área total del jardín rectangular?
Solución
Nuevamente, antes de tomar un enfoque algebraico, vamos a experimentar. Tenga en cuenta que hemos etiquetado el ancho con la letra x y la altura con la letra y en nuestro boceto del jardín en Figura\(\PageIndex{5}\).
Hay un total de 80 pies de material de barda. Supongamos que dejamos y = 5 pies. Debido a que hay tres lados de longitud y = 5 pies, hemos utilizado 15 pies de material. Eso deja 65 pies de material que se utilizará para cercar el ancho del jardín. Es decir, el ancho es x = 65 ft. Así, las dimensiones del jardín son x = 65 ft por y = 5 ft. El área es igual al producto de estas dos medidas, entonces\(A=325 \mathrm{ft}^{2}\). Pongamos este resultado en una mesa.
| x | y | A=XY |
|---|---|---|
| 65 pies | 5 pies | 325\(\text{ft}^{2}\) |
Supongamos en cambio que dejamos que la altura sea y = 10 pies. Nuevamente, hay tres secciones con esta longitud, por lo que esto tomará 30 pies de material. Eso deja 50 pies de material, por lo que el ancho x = 50 pies. El área es producto de estas dos medidas, entonces\(A=500 \mathrm{ft}^{2}\). Como tercer experimento, dejar que la altura y = 15 pies. Al restar tres de estas longitudes de 80 pies, vemos que el ancho x = 35 pies. El área es producto de estas medidas, entonces\(A=525 \mathrm{ft}^{2}\). Agreguemos estos dos últimos experimentos numéricos a nuestra mesa.
| x | y | A=XY |
|---|---|---|
| 65 pies | 5 pies | 325\(\text{ft}^{2}\) |
| 50 pies | 10 pies | 500\(\text{ft}^{2}\) |
| 35 pies | 15 pies | 525\(\text{ft}^{2}\) |
En este punto, el último conjunto de dimensiones arroja el área máxima, pero ¿es posible que otra opción de x e y produzca un área mayor? Experimente más con los números de su elección para ver si puede encontrar dimensiones que produzcan un área mayor que el máximo actual en la tabla, es decir 525\(\mathrm{ft}^{2}\).
Llamemos ahora a lo que hemos aprendido en esta sección para atacar a este modelo. Primero, estamos limitados por la cantidad de material que tenemos para el trabajo, un total de 80 pies de esgrima. Esta restricción requiere que 3 veces la altura del jardín, sumada a la anchura del jardín, sea igual a la cantidad disponible de material de cercado. En símbolos,
\[x+3 y=80\]
Se nos pide maximizar el área, por lo que enfocamos nuestros esfuerzos en encontrar una fórmula para el área del jardín rectangular. Debido a que el área A del jardín rectangular es producto de la anchura y la altura,\[A=x y\]
Ahora tenemos una fórmula para el área del jardín rectangular, pero desafortunadamente tenemos el área A en función de dos variables. Necesitamos eliminar una u otra de estas variables. Esto se hace fácilmente resolviendo la ecuación (18) para x.\[x=80-3 y\]
A continuación, sustituya este resultado en la ecuación (19) para obtener\[A=(80-3 y) y\]
o, equivalentemente,\[A=-3 y^{2}+80 y\]
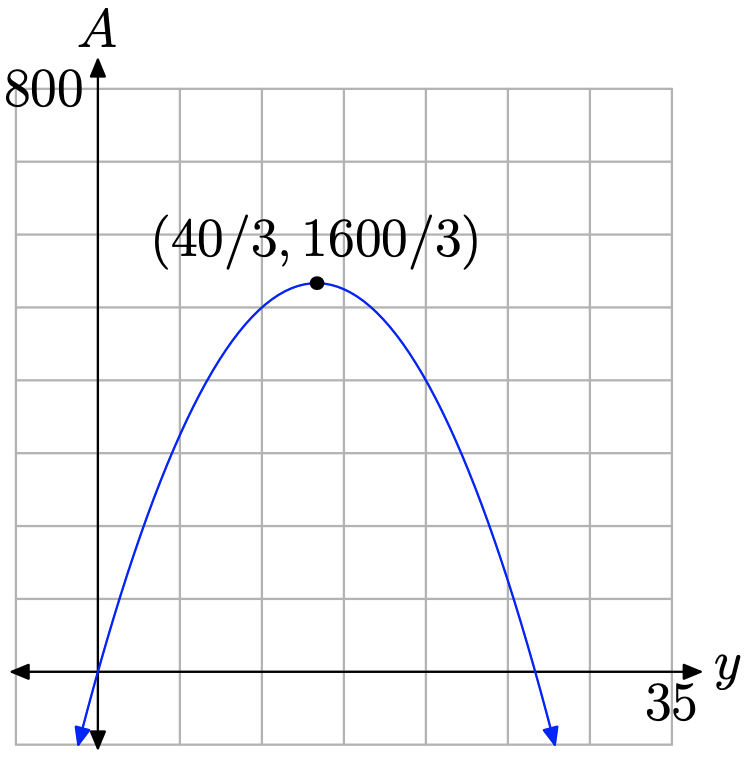
Obsérvese que hemos expresado el área A en función de una sola variable y, además, la función definida por la ecuación (21) es cuadrática. Comparar\(A=-3 y^{2}+80 y\) con la forma general\(A=a y^{2}+b y+c\) y anotar que a = −3 y b = 80 (no tenemos necesidad del hecho de que c = 0). Por lo tanto, si trazamos A versus y, la gráfica es una parábola que se abre hacia abajo (ver Figura\(\PageIndex{6}\)), por lo que el valor máximo de A ocurrirá en el vértice. La coordenada y del vértice se encuentra con
\[y_{\mathrm{vertex}}=-\frac{b}{2 a}=-\frac{80}{2(-3)}=\frac{80}{6}=\frac{40}{3}\]
Para encontrar el ancho del jardín rectangular, sustituya y = 40/3 en la ecuación (20) y resuelva por x.
\[x=80-3 y=80-3\left(\frac{40}{3}\right)=80-40=40\]
Así, el ancho del jardín rectangular es de 40 pies. Podemos encontrar el área del jardín multiplicando el ancho y la altura.
\[A=x y=(40)\left(\frac{40}{3}\right)=\frac{1600}{3}=533 \frac{1}{3}\]
Tenga en cuenta que el área resultante,\(A=533 \frac{1}{3} \mathrm{ft}^{2}\), es solo un poco más grande la última entrada tabular encontrada con nuestros experimentos numéricos.
También se puede encontrar el área de la región rectangular sustituyendo y = 40/3 en la ecuación (21). Dejaremos que nuestros lectores verifiquen que esto proporciona la misma medida para el área. También notarás que la segunda coordenada del vértice en la Figura\(\PageIndex{6}\) es el área máxima\(A=1600 / 3 \mathrm{ft}^{2}\).
Ejercicio
Ejercicio\(\PageIndex{1}\)
Encuentra el valor máximo exacto de la función\(f(x) = −x^2−3x\).
- Contestar
-
\(\frac{9}{4}\)
Ejercicio\(\PageIndex{2}\)
Encuentra el valor máximo exacto de la función\(f(x) = −x^2−5x−2\).
Ejercicio\(\PageIndex{3}\)
Encuentra el vértice de la gráfica de la función\(f(x) = −3x^2−x−6\).
- Contestar
-
\((−\frac{1}{6}, −\frac{71}{12})\)
Ejercicio\(\PageIndex{4}\)
Encuentra el rango de la función\(f(x) = −2x^2−9x+2\).
Ejercicio\(\PageIndex{5}\)
Encuentra el valor máximo exacto de la función\(f(x) = −3x^2−9x−4\).
- Contestar
-
\(\frac{11}{4}\)
Ejercicio\(\PageIndex{6}\)
Encuentra la ecuación del eje de simetría de la gráfica de la función\(f(x) = −x^2−5x−9\).
Ejercicio\(\PageIndex{7}\)
Encuentra el vértice de la gráfica de la función\(f(x) = 3x^2+3x+9\).
- Contestar
-
\((−\frac{1}{2}, \frac{33}{4})\)
Ejercicio\(\PageIndex{8}\)
Encuentra el valor mínimo exacto de la función\(f(x) = x^2+x+1\).
Ejercicio\(\PageIndex{9}\)
Encuentra el valor mínimo exacto de la función\(f(x) = x^2+9x\).
- Contestar
-
\(−\frac{81}{4}\)
Ejercicio\(\PageIndex{10}\)
Encuentra el rango de la función\(f(x) = 5x^2−3x−4\).
Ejercicio\(\PageIndex{11}\)
Encuentra el rango de la función\(f(x) = −3x^2+8x−2\).
- Contestar
-
\((−\infty, \frac{10}{3}]\)= {\(x|x \le \frac{10}{3}\)}
Ejercicio\(\PageIndex{12}\)
Encuentra el valor mínimo exacto de la función\(f(x) = 2x^2+5x−6\).
Ejercicio\(\PageIndex{13}\)
Encuentra el rango de la función\(f(x) = 4x^2+9x−8\).
- Contestar
-
\([−\frac{209}{16}, \infty)\)= {\(x|x \ge −\frac{209}{16}\)}
Ejercicio\(\PageIndex{14}\)
Encuentra el valor máximo exacto de la función\(f(x) = −3x^2−8x−1\).
Ejercicio\(\PageIndex{15}\)
Encuentra la ecuación del eje de simetría de la gráfica de la función\(f(x) = −4x^2−2x+9\).
- Contestar
-
\(x = −\frac{1}{4}\)
Ejercicio\(\PageIndex{16}\)
Encuentra el valor mínimo exacto de la función\(f(x) = 5x^2+2x−3\).
Ejercicio\(\PageIndex{17}\)
Se lanza una pelota hacia arriba a una velocidad de 8 pies/s desde lo alto de un edificio de 182 pies de altura. ¿Cuántos segundos tarda la pelota en alcanzar su máxima altura? Redondee su respuesta a la centésima de segundo más cercana.
- Contestar
-
0.25
Ejercicio\(\PageIndex{18}\)
Se lanza una pelota hacia arriba a una velocidad de 9 pies/s desde lo alto de un edificio de 143 pies de altura. ¿Cuántos segundos tarda la pelota en alcanzar su máxima altura? Redondee su respuesta a la centésima de segundo más cercana.
Ejercicio\(\PageIndex{19}\)
Se lanza una pelota hacia arriba a una velocidad de 52 pies/s desde lo alto de un edificio de 293 pies de altura. ¿Cuál es la altura máxima de la pelota? Redondee su respuesta a la centésima de pie más cercana.
- Contestar
-
335. 25
Ejercicio\(\PageIndex{20}\)
Se lanza una pelota hacia arriba a una velocidad de 23 pies/s desde lo alto de un edificio de 71 pies de altura. ¿Cuál es la altura máxima de la pelota? Redondee su respuesta a la centésima de pie más cercana.
Ejercicio\(\PageIndex{21}\)
Encuentra dos números cuya suma sea 20 y cuyo producto sea un máximo.
- Contestar
-
10 y 10
Ejercicio\(\PageIndex{22}\)
Encuentra dos números cuya suma sea 36 y cuyo producto sea máximo.
Ejercicio\(\PageIndex{23}\)
Encuentra dos números cuya diferencia sea 12 y cuyo producto sea mínimo.
- Contestar
-
6 y −6
Ejercicio\(\PageIndex{24}\)
Encuentra dos números cuya diferencia es 24 y cuyo producto es mínimo.
Ejercicio\(\PageIndex{25}\)
Un número es 3 más grande que dos veces por segundo número. Encuentra dos de esos números para que su producto sea mínimo.
- Contestar
-
\(\frac{3}{2}\)y\(−\frac{3}{4}\)
Ejercicio\(\PageIndex{26}\)
Un número es 2 mayor que 5 veces un segundo número. Encuentra dos de esos números para que su producto sea mínimo.
Ejercicio\(\PageIndex{27}\)
Entre todos los pares de números cuya suma es − 10, encuentra el par de tal manera que la suma de sus cuadrados sea la menor posible.
- Contestar
-
−5, −5
Ejercicio\(\PageIndex{28}\)
Entre todos los pares de números cuya suma es − 24, encuentra el par de tal manera que la suma de sus cuadrados sea la menor posible.
Ejercicio\(\PageIndex{29}\)
Entre todos los pares de números cuya suma es 14, encuentra el par de tal manera que la suma de sus cuadrados sea la menor posible.
- Contestar
-
7, 7
Ejercicio\(\PageIndex{30}\)
Entre todos los pares de números cuya suma es 12, encuentra el par de tal manera que la suma de sus cuadrados sea la menor posible.
Ejercicio\(\PageIndex{31}\)
Entre todos los rectángulos que tienen perímetro de 40 pies, encuentra las dimensiones (largo y ancho) del que tiene mayor área.
- Contestar
-
10 pies por 10 pies
Ejercicio\(\PageIndex{32}\)
Entre todos los rectángulos que tienen perímetro de 100 pies, encuentra las dimensiones (largo y ancho) del que tiene mayor área.
Ejercicio\(\PageIndex{33}\)
Un agricultor con 1700 metros de esgrima quiere encerrar una parcela rectangular que bordea en un río. Si no se requiere barda a lo largo del río, ¿cuál es el área más grande que se puede encerrar?
- Contestar
-
361250 metros cuadrados
Ejercicio\(\PageIndex{34}\)
Un ranchero con 1500 metros de esgrima quiere encerrar una parcela rectangular que bordea sobre un río. Si no se requiere barda a lo largo del río, y el lado paralelo al río es de x metros de largo, encuentre el valor de x que dará el área más grande del rectángulo.
Ejercicio\(\PageIndex{35}\)
Un guardabosques con 400 metros de esgrima quiere encerrar una parcela rectangular que bordea en un río. Si no se requiere barda a lo largo del río, y el lado paralelo al río es de x metros de largo, encuentre el valor de x que dará el área más grande del rectángulo.
- Contestar
-
200
Ejercicio\(\PageIndex{36}\)
Un ranchero con 1000 metros de esgrima quiere encerrar una parcela rectangular que bordea sobre un río. Si no se requiere barda a lo largo del río, ¿cuál es el área más grande que se puede encerrar?
Ejercicio\(\PageIndex{37}\)
Que x represente la demanda (el número que el público va a comprar) de un objeto y dejar que p represente el precio unitario del objeto (en dólares). Supongamos que el precio unitario y la demanda están linealmente relacionados por la ecuación\(p = −\frac{1}{3}x + 40\).
- Exprese los ingresos R (la cantidad ganada por la venta de los objetos) en función de la demanda x.
- Encuentra la demanda que maximizará los ingresos.
- Encuentra el precio unitario que maximizará los ingresos.
- ¿Cuál es el ingreso máximo?
- Contestar
-
- \(R = −\frac{1}{3}x^2+40x\)
- x = 60 objetos
- p = 20 dólares
- R = $1200
Ejercicio\(\PageIndex{38}\)
Que x represente la demanda (el número que el público va a comprar) de un objeto y dejar que p represente el precio unitario del objeto (en dólares). Supongamos que el precio unitario y la demanda están linealmente relacionados por la ecuación\(p = −\frac{1}{5}x + 200\).
- Exprese los ingresos R (la cantidad ganada por la venta de los objetos) en función de la demanda x.
- Encuentra la demanda que maximizará los ingresos.
- Encuentra el precio unitario que maximizará los ingresos.
- ¿Cuál es el ingreso máximo?
Ejercicio\(\PageIndex{39}\)
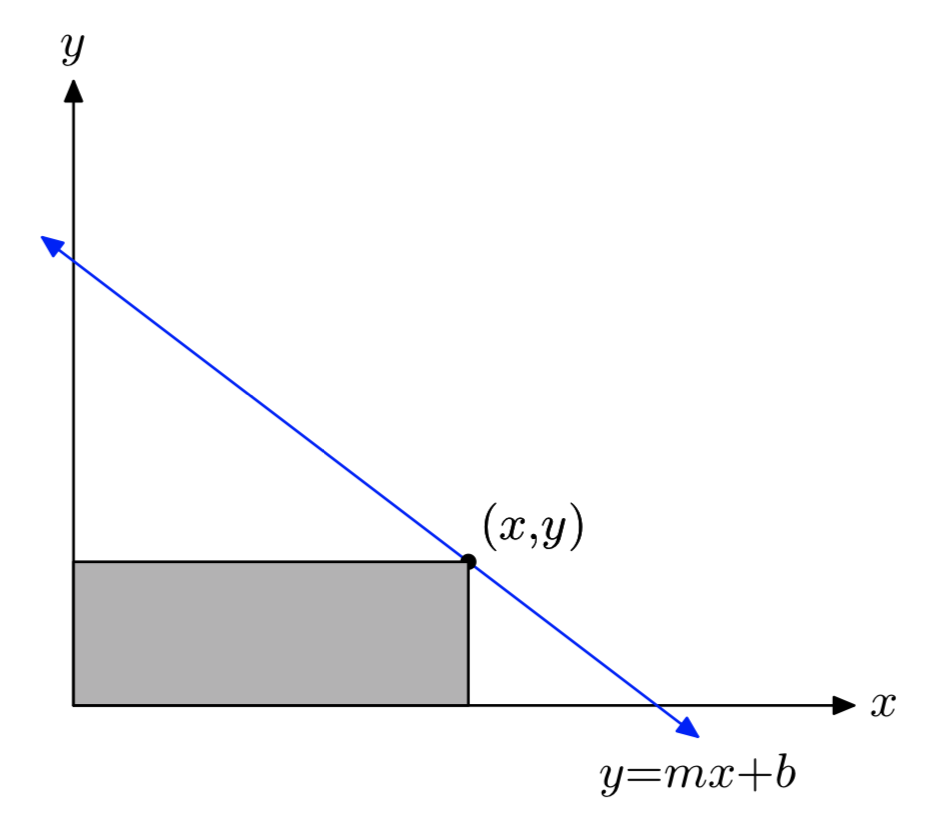
Se selecciona un punto del primer cuadrante en la línea y = mx + b. Desde este punto se dibujan líneas paralelas a los ejes para formar un rectángulo debajo de la línea del primer cuadrante. Entre todos esos rectángulos, encuentra las dimensiones del rectángulo con área máxima. ¿Cuál es el área máxima? Supongamos m < 0.
- Contestar
-
\(x = −\frac{b}{2m}\),
\(y = \frac{b}{2}\),
\(A = −\frac{b^2}{4m}\)
Ejercicio\(\PageIndex{40}\)
Un ranchero desea cercar un área rectangular. Los lados este-oeste del rectángulo requerirán un soporte más fuerte debido a los vientos de tormenta este-oeste predominantes. En consecuencia, el costo del cercado para los lados este-oeste del área rectangular es de 18 dólares por pie. El costo de cercar los lados norte-sur del área rectangular es de 12 dólares por pie. Encuentre la dimensión del área rectangular más grande posible que se pueda cercar por $7200.


