5.1: La Parábola

En esta sección aprenderás a dibujar la gráfica de la función cuadrática definida por la ecuación

$$f(x)=a(x-h)^{2}+k \label{eq1}$$

Rápidamente aprenderás que la gráfica de la función cuadrática tiene forma de “U” y se llama parábola. La forma de la función cuadrática en la Ecuación\ ref {eq1} se llama forma de vértice, así llamada porque la forma revela fácilmente el vértice o “punto de inflexión” de la parábola. Cada una de las constantes en la forma de vértice de la función cuadrática juega un papel. Como pronto verás, la constante a controla el escalado (estiramiento o compresión de la parábola), la constante h controla un desplazamiento horizontal y la colocación del eje de simetría, y la constante$k$ controla el desplazamiento vertical. Empecemos por mirar el escalamiento de la cuadrática.

Escalando la Cuadrática

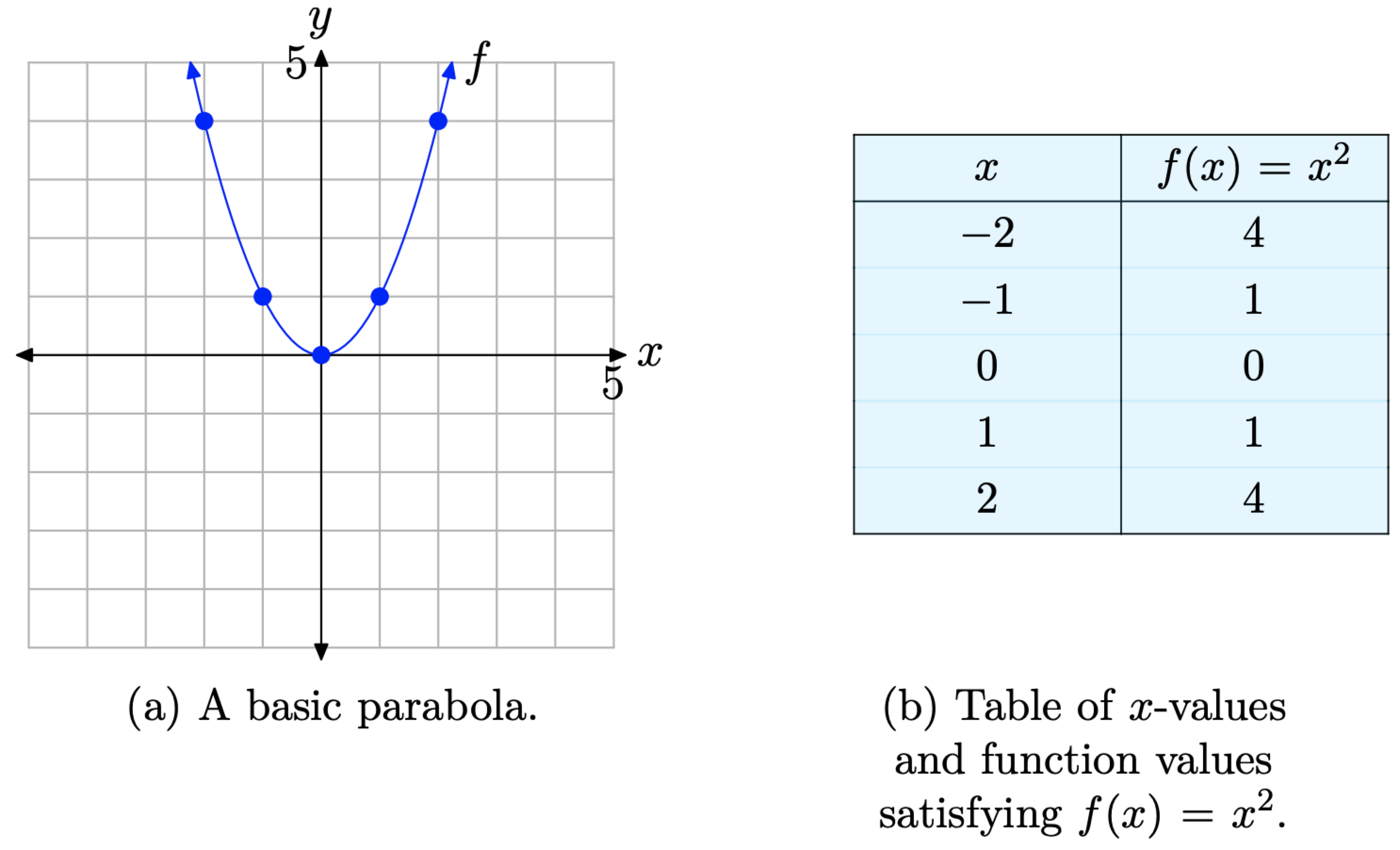
La gráfica de la función cuadrática básica$f(x)=x^{2}$ mostrada en la Figura$\PageIndex{1}$ (a) es una parábola. Decimos que la parábola de la Figura$\PageIndex{1}$ (a) “se abre hacia arriba”. El punto en (0, 0), el “punto de inflexión” de la parábola, se llama el vértice de la parábola. Hemos tabulado algunos puntos para referencia en la tabla de la Figura$\PageIndex{1}$ (b) y luego superpuesto estos puntos en la gráfica de$f(x)=x^{2}$ la Figura$\PageIndex{1}$ (a).

Figura$\PageIndex{1}$: La gráfica de la parábola básica es un punto de partida fundamental.

Ahora que conocemos la forma básica de la parábola determinada por$f(x) = x^{2}$, veamos qué sucede cuando escalamos la gráfica de$f(x) = x^{2}$ en dirección vertical. Por ejemplo, investiguemos la gráfica de$g(x) = 2x^{2}$. El factor de 2 tiene un efecto de duplicación. Obsérvese que cada uno de los valores de función de g es el doble del valor de función correspondiente de f en la tabla de la Figura$\PageIndex{2}$ (b).

Figura$\PageIndex{2}$: Un estiramiento por un factor de 2 en la dirección vertical.

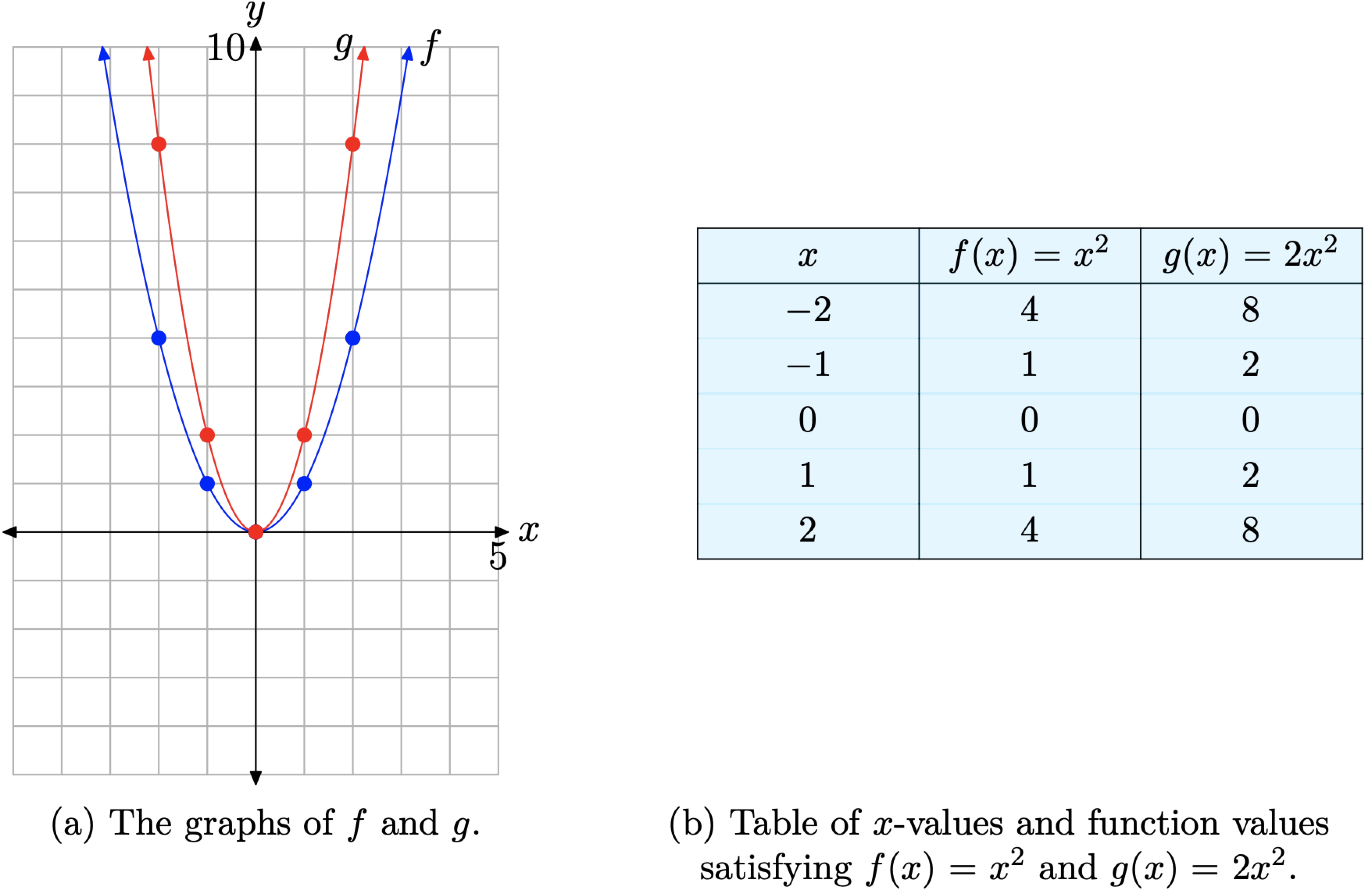
Cuando los puntos de la tabla de la Figura$\PageIndex{2}$ (b) se agregan al sistema de coordenadas de la Figura$\PageIndex{2}$ (a), la gráfica resultante de g se estira por un factor de dos en la dirección vertical. Es como si hubiéramos puesto la gráfica original de f en una hoja de papel cuadriculado de goma, agarramos los bordes superior e inferior de la hoja, y luego tiramos de cada borde en dirección vertical para estirar la gráfica de f por un factor de dos. En consecuencia, la gráfica de$g(x) = 2x^{2}$ aparece algo más estrecha en apariencia, como se ve en comparación con la gráfica de$f(x) = x^{2}$ la Figura$\PageIndex{2}$ (a). Tenga en cuenta, sin embargo, que el vértice en el origen no se ve afectado por esta escala.

De igual manera, para dibujar la gráfica de$h(x) = 3x^{2}$, tomar la gráfica de$f(x) = x^{2}$ y estirar la gráfica por un factor de tres, triplicando el valor y de cada punto en la gráfica original de f. Esta idea lleva al siguiente resultado.

Propiedad 2

Si a es una constante mayor que 1, es decir, si$a > 1$, entonces la gráfica de$g(x) = ax^{2}$, cuando se compara con la gráfica de$f(x) = x^{2}$, se estira por un factor de a.

Ejemplo$\PageIndex{1}$

Compara las gráficas de$y = x^{2}$$y = 2x ^{2}$, y$y = 3x^{2}$ en tu calculadora gráfica.

Solución

Cargue las funciones$y = x^{2}$$y = 2x ^{2}$, y$y = 3x^{2}$ en el menú Y=, como se muestra en la Figura$\PageIndex{3}$ (a). Pulse el botón ZOOM y seleccione 6:ZStandard para producir la imagen que se muestra en la Figura$\PageIndex{3}$ (b).

Figura$\PageIndex{3}$: Dibujo$y = x^{2}$,$y = 2x ^{2}$, y$y = 3x^{2}$ en la calculadora gráfica.

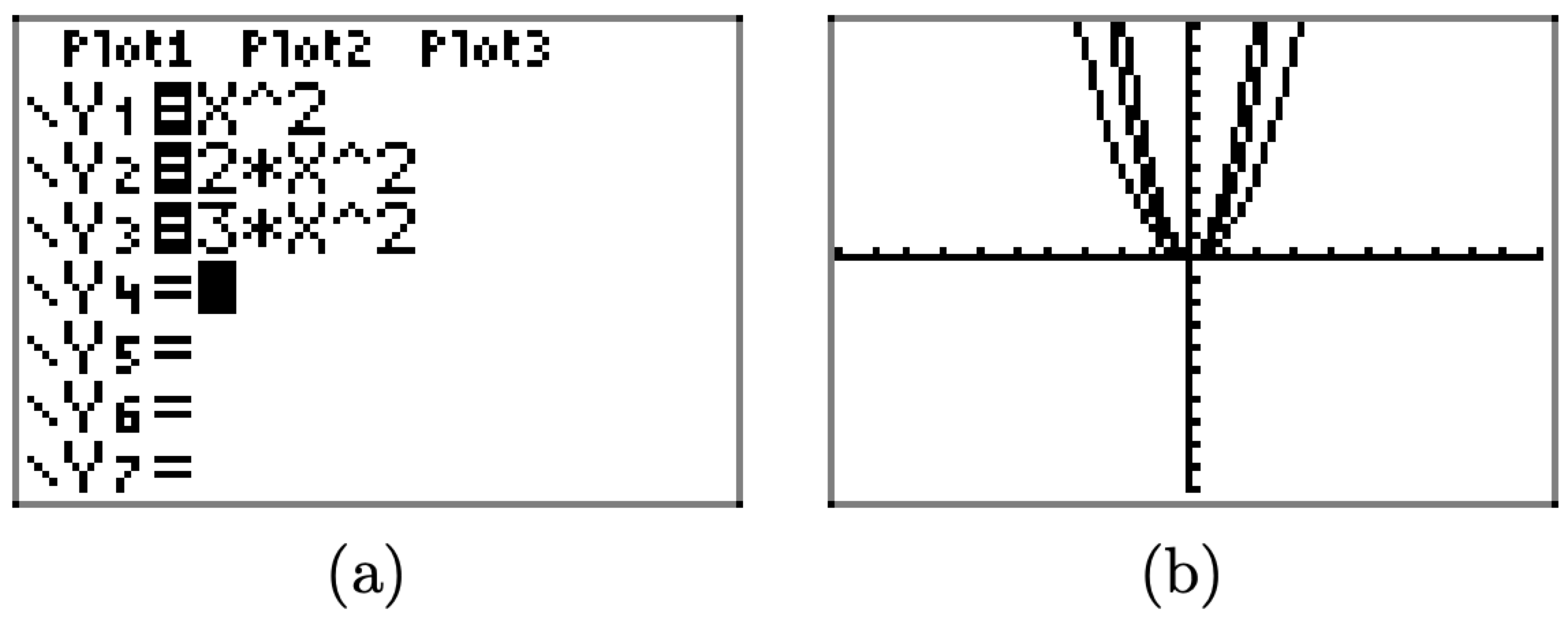
Tenga en cuenta que a medida que la “a” en$y = ax^{2}$ aumenta de 1 a 2 a 3, la gráfica de$y = ax^{2}$ se estira más y se vuelve, en cierto sentido, más estrecha en apariencia.

A continuación, consideremos qué sucede cuando escalamos por un número que es menor que 1 (pero mayor que cero — trataremos con lo negativo en un momento). Por ejemplo, investiguemos la gráfica de$g(x) = (1/2)x^{2}$. El factor 1/2 tiene un efecto de halving. Obsérvese que cada uno de los valores de función de g es la mitad del valor de función correspondiente de f en la tabla de la Figura$\PageIndex{4}$ (b).

Figura$\PageIndex{4}$: Una compresión por un factor de 2 en la dirección vertical.

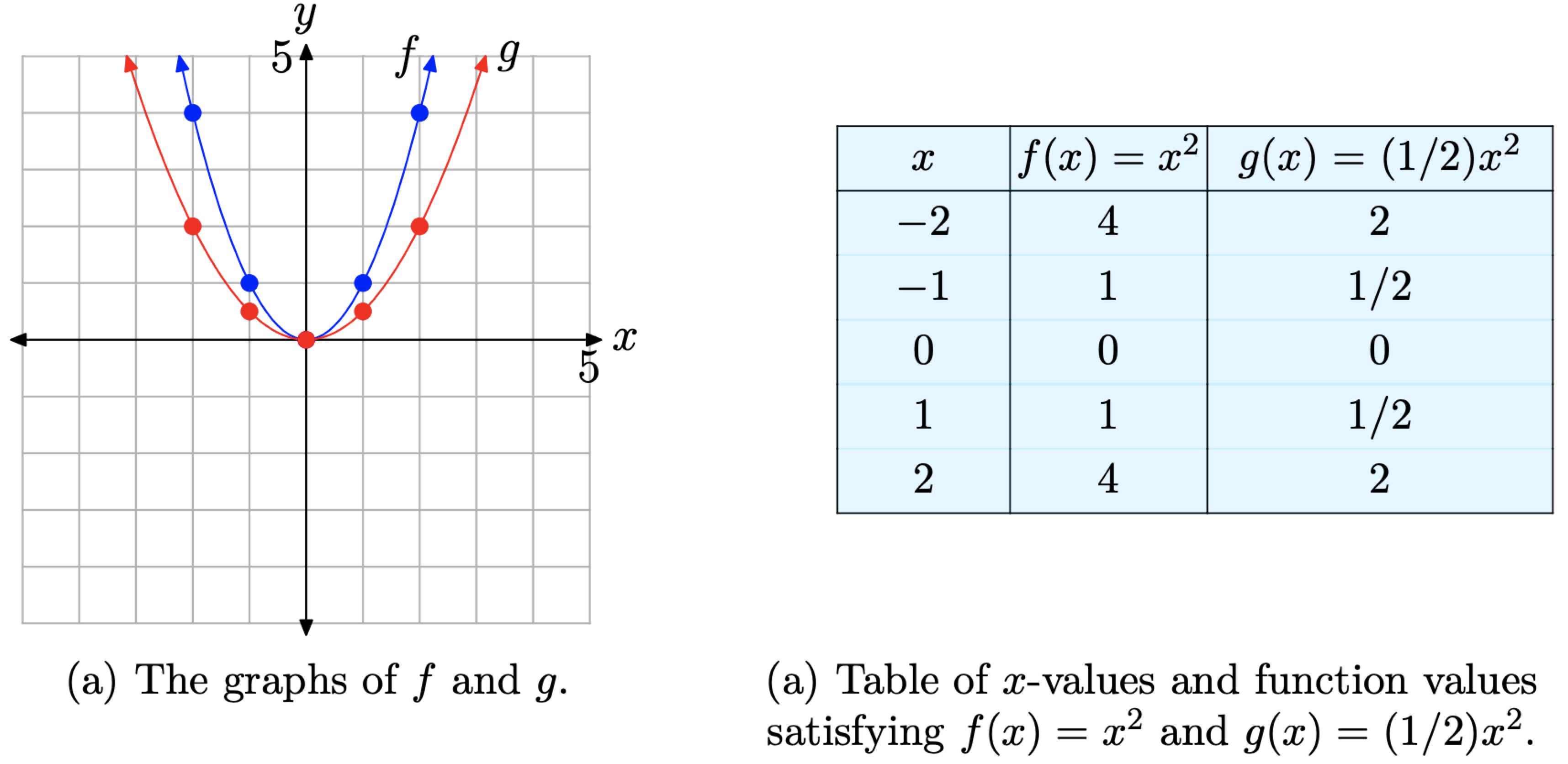
Cuando los puntos de la tabla de la Figura$\PageIndex{4}$ (b) se agregan al sistema de coordenadas de la Figura$\PageIndex{4}$ (a), la gráfica resultante de g se comprime por un factor de 2 en la dirección vertical. Es como si volviéramos a colocar la gráfica de$f(x) = x^{2}$ sobre una hoja de papel cuadriculado de goma, agarráramos la parte superior e inferior de la hoja, y luego las apretáramos juntas por un factor de dos. En consecuencia, la gráfica de$g(x) = (1/2)x^{2}$ aparece algo más amplia en apariencia, como se ve en comparación con la gráfica de$f(x) = x^{2}$ la Figura$\PageIndex{4}$ (a). Obsérvese nuevamente que el vértice en el origen no se ve afectado por esta escala.

Propiedad 4

Si a es una constante menor que 1 (pero mayor que cero), es decir, si$0 < a < 1$, entonces la gráfica de$g(x) = ax^{2}$, cuando se compara con la gráfica de$f(x) = x^{2}$, se comprime por un factor de 1/a.

Algunos encuentran la propiedad 4 algo contraintuitiva. Sin embargo, si comparas la función$g(x) = (1/2)x^2$ con la forma general$g(x) = ax^2$, ves que a = 1/2. La propiedad 4 establece que la gráfica será comprimida por un factor de 1/a. en este caso, a = 1/2 y

$$\frac{1}{a}=\frac{1}{1 / 2}=2$$

Así, la Propiedad 4 establece que la gráfica de$g(x) = (1/2)x^2$ debe ser comprimida por un factor de 1/ (1/2) o 2, lo que se ve como el caso en la Figura$\PageIndex{4}$ (a).

Ejemplo$\PageIndex{2}$

Compara las gráficas de$y=x^{2}, y=(1 / 2) x^{2},$ y$y=(1 / 3) x^{2}$ en tu calculadora gráfica.

Solución

Cargue las ecuaciones$y=x^{2}, y=(1 / 2) x^{2},$ y$y=(1 / 3) x^{2}$ en el Y=, como se muestra en la Figura$\PageIndex{5}$ (a). Pulse el botón ZOOM y seleccione 6:ZStandard para producir la imagen que se muestra en la Figura$\PageIndex{5}$ (b).

Figura$\PageIndex{5}$: Dibujo$y=x^{2}, y=(1 / 2) x^{2},$ y$y=(1 / 3) x^{2}$ en la calculadora gráfica.

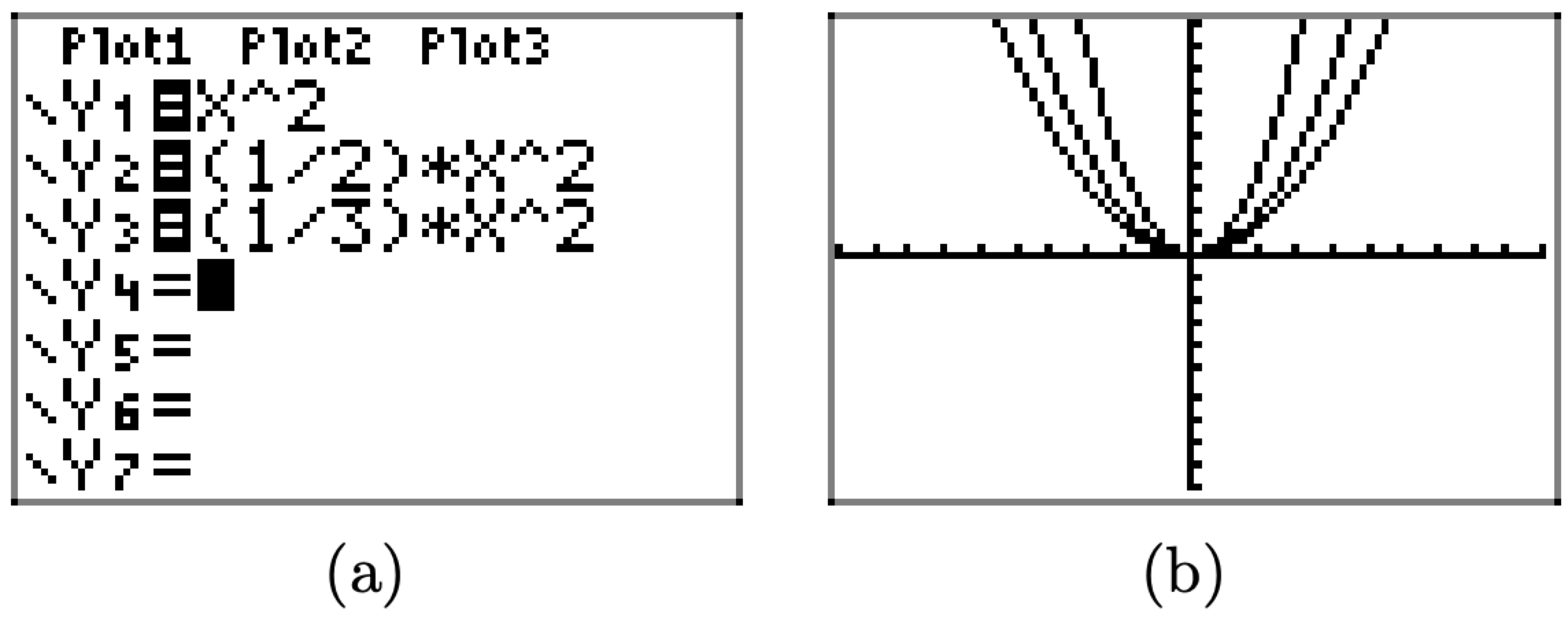
Tenga en cuenta que a medida que la “a” en$y = ax^2$ disminuye de 1 a 1/2 a 1/3, la gráfica de$y = ax^2$ comprime más y se vuelve, en cierto sentido, más amplia en apariencia.

Reflexiones Verticales

Consideremos la gráfica de$g(x) = ax^2$, cuando un < 0. Por ejemplo, considere las gráficas de$g(x)=-x^{2}$ y$h(x)=(-1 / 2) x^{2}$ en la Figura$\PageIndex{6}$

Figura$\PageIndex{6}$: Reflexión vertical a través del eje x.

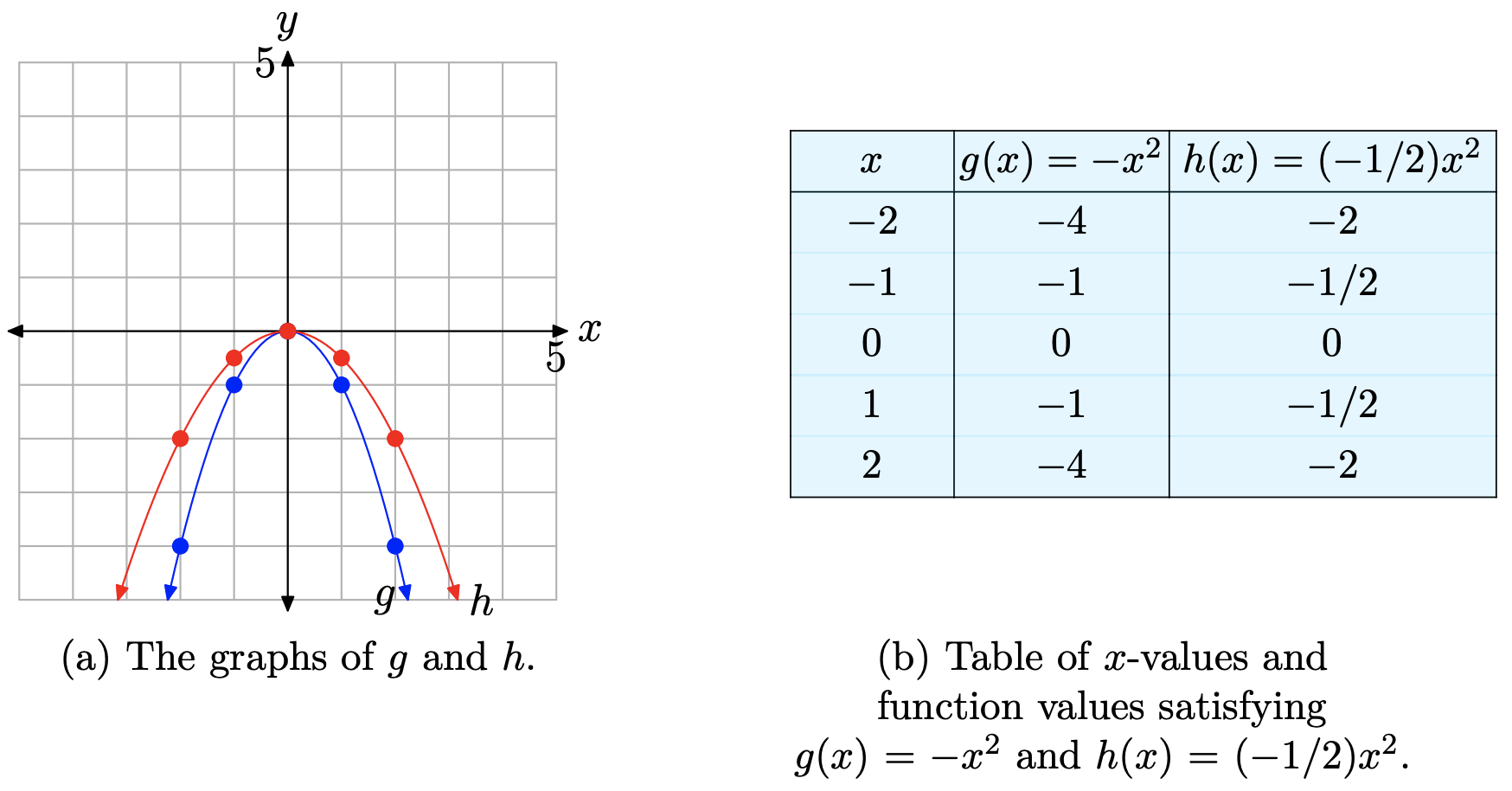
Cuando se compara la tabla de la Figura$\PageIndex{6}$ (b) con la tabla de la Figura$\PageIndex{4}$ (b), es fácil ver que los números en las dos últimas columnas son los mismos, pero han sido negados. El resultado es fácil de ver en la Figura$\PageIndex{6}$ (a). Las gráficas se han reflejado a través del eje x. Cada una de las parábolas ahora “se abre hacia abajo”.

No obstante, es alentador ver que el papel escalador de la constante a in no$g(x) = ax^2$ ha cambiado. En el caso de$h(x) = (−1/2)x^2$, los valores y todavía están “comprimidos” por un factor de dos, pero el signo menos niega estos valores, haciendo que la gráfica se refleje a través del eje x. Así, por ejemplo, uno pensaría que la gráfica de se$y = −2x^2$ estiraría por un factor de dos, luego se reflejaría a través del eje x. En efecto, esto es correcto, y esta discusión lleva a la siguiente propiedad.

Propiedad 6

Si$−1 < a < 0$, entonces la gráfica de$g(x) = ax^2$, cuando se compara con la gráfica de$f(x) = x^2$, se comprime por un factor de 1/|a|, luego se refleja a través del eje x. En segundo lugar, si a < −1, entonces la gráfica de$g(x) = ax^2$, cuando se compara con la gráfica de$f(x) = x^2$, se estira por un factor de |a|, luego se refleja a través del eje x.

Nuevamente, algunos encuentran confuso la Propiedad 6. No obstante, si se compara$g(x) = (−1/2)x^2$ con la forma general$g(x) = ax^2$, se ve que a = −1/2. Tenga en cuenta que en este caso, −1 < a < 0. La propiedad 6 establece que la gráfica será comprimida por un factor de 1/|a|. En este caso, a = −1/2 y

$$\frac{1}{|a|}=\frac{1}{|-1 / 2|}=2$$

Es decir, la Propiedad 6 establece que la gráfica de$g(x) = (−1/2)x^2$ está comprimida por un factor de 1/ (| − 1/2|), o 2, luego se refleja a través del eje x, que se ve como el caso en la Figura$\PageIndex{6}$ (a). Obsérvese nuevamente que el vértice en el origen no se ve afectado por esta escala y reflexión.

Ejemplo$\PageIndex{3}$

Esboce los gráficos de$y=-2 x^{2}, y=-x^{2},$ y$y=(-1 / 2) x^{2}$ en su calculadora gráfica

Solución

Cada una de las ecuaciones se cargaron por separado en Y1 en el menú Y=. En cada una de las imágenes de la Figura$\PageIndex{7}$, seleccionamos 6:ZStandard del menú ZOOM para producir la imagen.

Figura$\PageIndex{7}$.

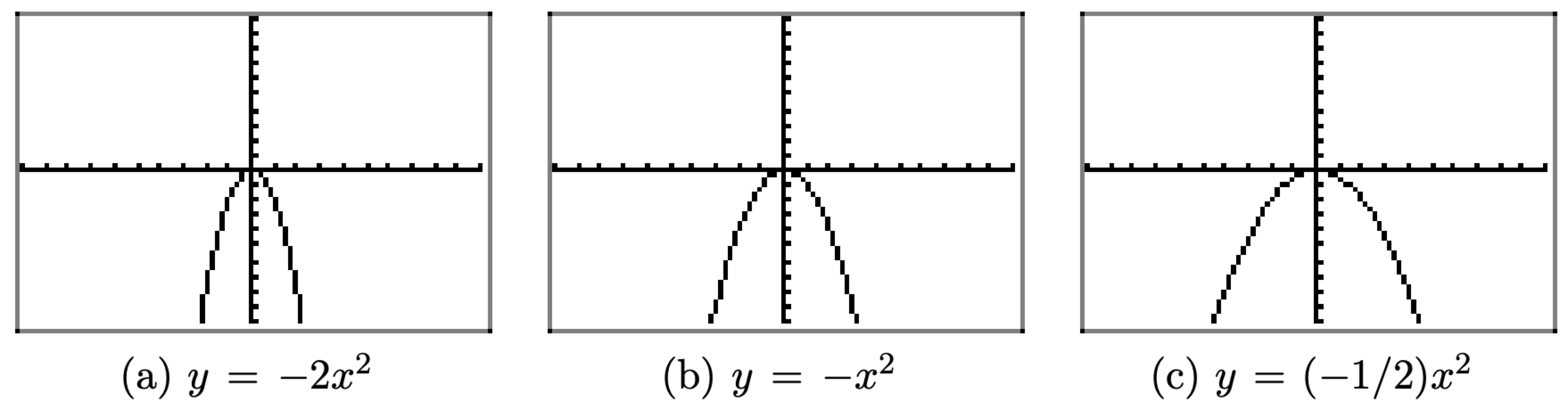
En la Figura$\PageIndex{7}$ (b), la gráfica de$y = −x^2$ es un reflejo de la gráfica de$y = x^2$ a través del eje x y se abre hacia abajo. En la Figura$\PageIndex{7}$ (a), nótese que la gráfica de$y = −2x^2$ se estira verticalmente por un factor de 2 (compárese con la gráfica de$y = −x^2$ la Figura$\PageIndex{7}$ (b)) y se refleja a través del eje x para abrirse hacia abajo. En la Figura$\PageIndex{7}$ (c), la gráfica de$(−1/2)x^2$ está comprimida por un factor de 2, aparece un poco más ancha y se refleja a través del eje x para abrirse hacia abajo.

Traducciones Horizontales

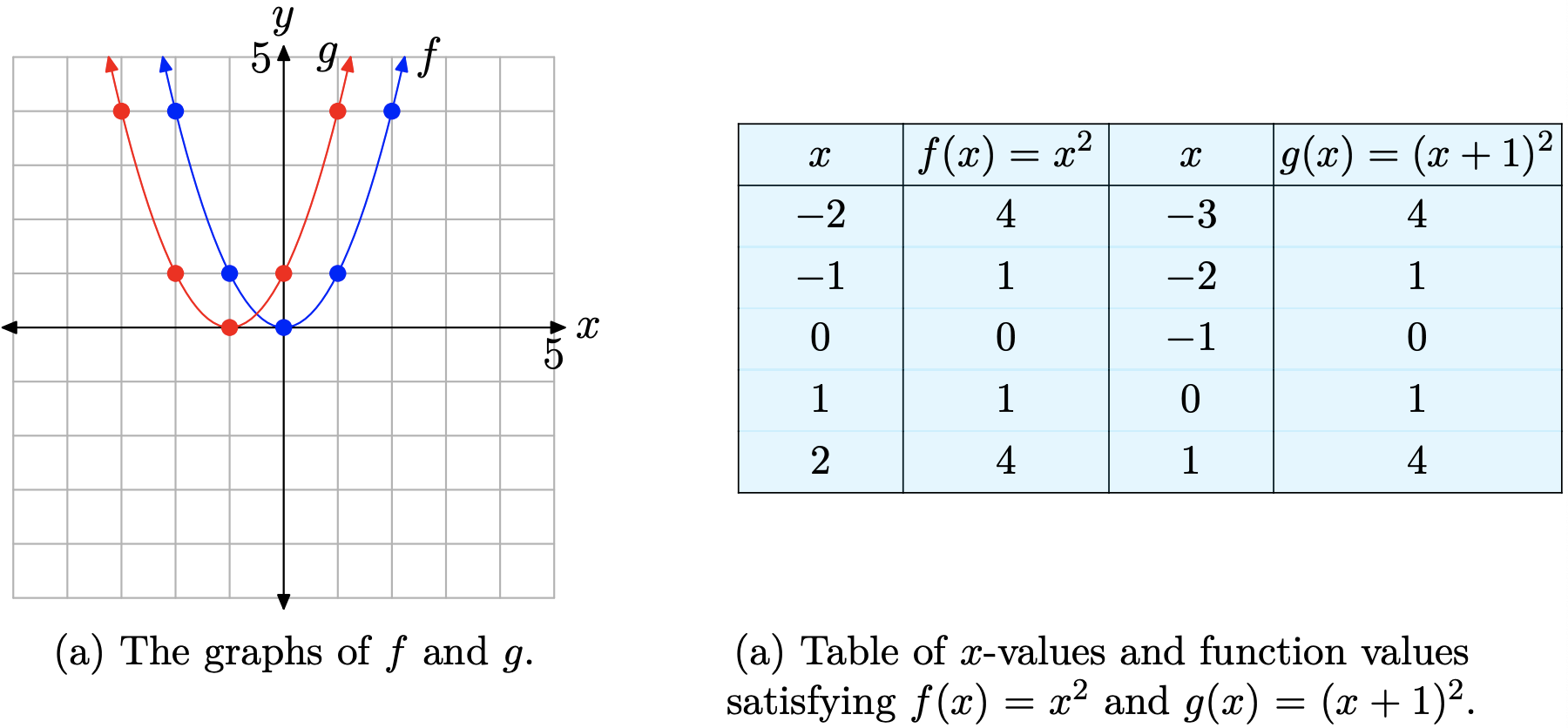
La gráfica de$g(x) = (x + 1)^2$ la Figura$\PageIndex{8}$ (a) muestra una parábola básica que se desplaza una unidad hacia la izquierda. Examine la tabla de la Figura$\PageIndex{8}$ (b) y observe que la ecuación$g(x) = (x + 1)^2$ produce los mismos valores y que la ecuación$f(x) = x^2$, siendo la única diferencia que estos valores y se calculan a valores x que son una unidad menos que los utilizados para$f(x) = x^2$. En consecuencia, la gráfica de$g(x) = (x + 1)^2$ debe desplazar una unidad a la izquierda de la gráfica de$f(x) = x^2$, como se evidencia en la Figura$\PageIndex{8}$ (a).

Tenga en cuenta que este resultado es contraintuitivo. Uno pensaría que reemplazar x por x + 1 desplazaría la gráfica una unidad hacia la derecha, pero el desplazamiento realmente ocurre en la dirección opuesta.

Por último, tenga en cuenta que esta vez el vértice de la parábola se ha desplazado 1 unidad hacia la izquierda y ahora se ubica en el punto (−1, 0).

Nos llevan a la siguiente conclusión.

Propiedad 8

Si c > 0, entonces la gráfica de$g(x) = (x + c)^2$ se desplaza c unidades a la izquierda de la gráfica de$f(x) = x^2$.

Figura$\PageIndex{8}$: Un desplazamiento horizontal o traslación.

Algo similar sucede cuando se reemplaza x por x − 1, solo que esta vez la gráfica se desplaza una unidad a la derecha.

Ejemplo$\PageIndex{4}$

Esboce los gráficos de$y=x^{2}$ y$y=(x-1)^{2}$ en su calculadora gráfica.

Solución

Cargue las ecuaciones$y = x^2$ y$y = (x − 1)^2$ en el menú Y=, como se muestra en la Figura$\PageIndex{9}$ (a). Pulse el botón ZOOM y seleccione 6:ZStandard para producir la imagen que se muestra en la Figura$\PageIndex{9}$ (b).

Figura$\PageIndex{9}$: Dibujo$y = x^2$ y$y = (x−1)^2$ en la calculadora gráfica.

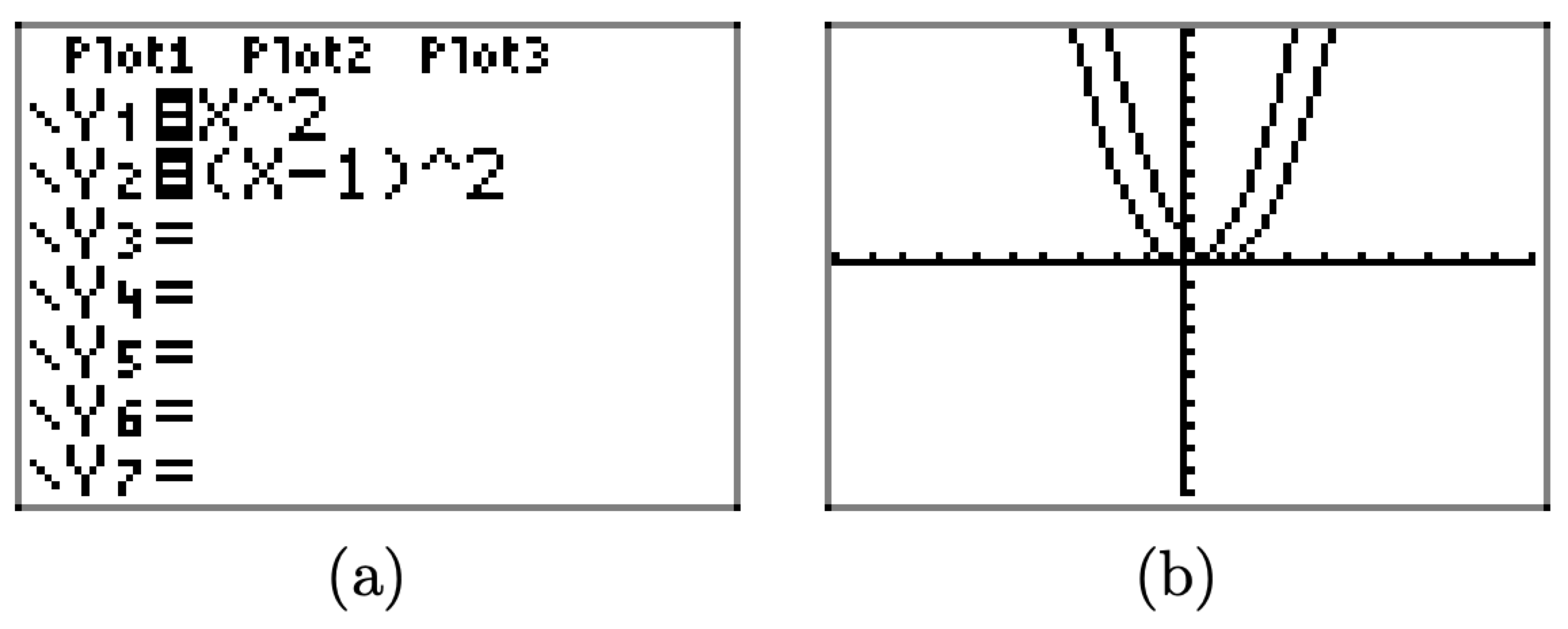
Obsérvese que la gráfica de$y = (x − 1)^2$ se desplaza 1 unidad a la derecha de la gráfica de$y = x^2$ y el vértice de la gráfica de ahora$y = (x − 1)^2$ se ubica en el punto (1, 0).

Nos llevan a la siguiente propiedad.

Propiedad 10

Si c > 0, entonces la gráfica de$g(x) = (x − c)^2$ se desplaza c unidades a la derecha de la gráfica de$f(x) = x^2$.

Traducciones Verticales

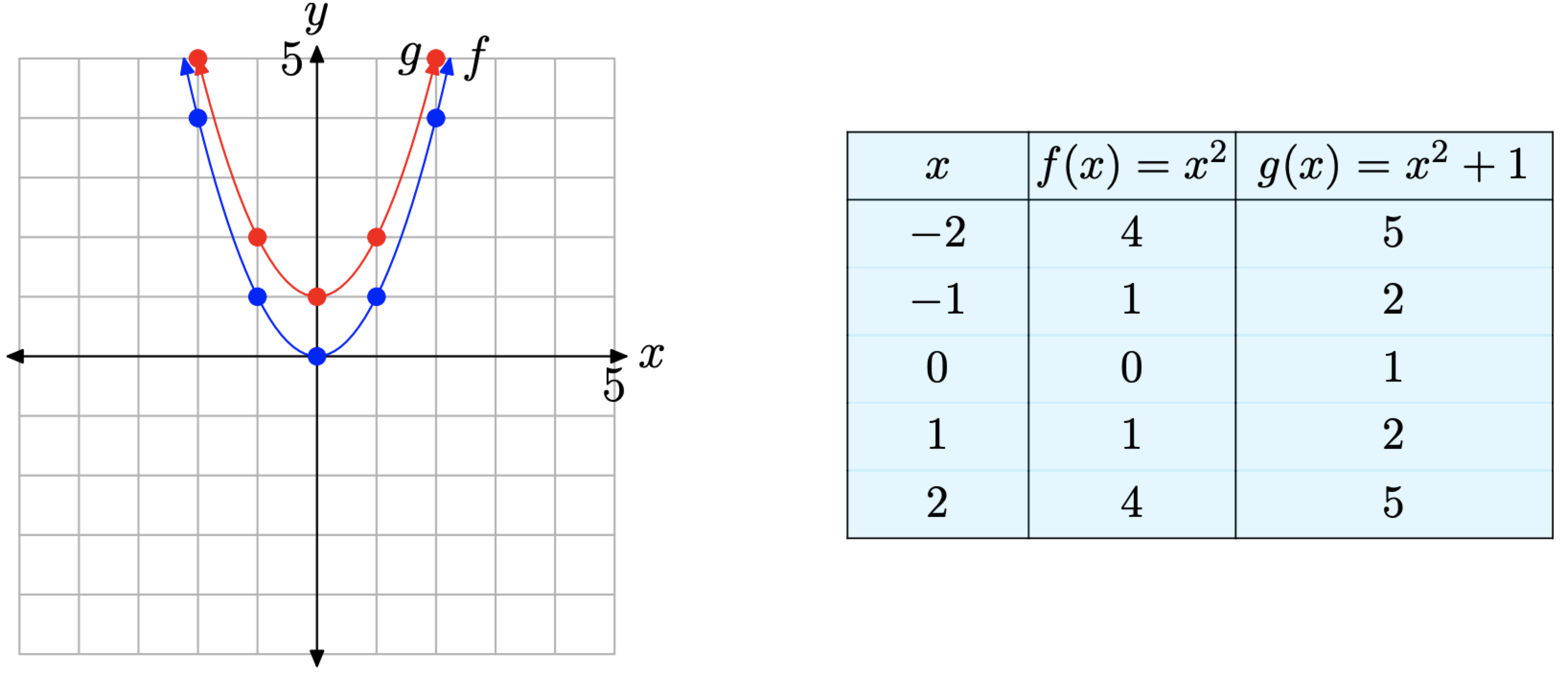
La gráfica de$g(x) = x^2 + 1$ la Figura$\PageIndex{10}$ (a) se desplaza una unidad hacia arriba de la gráfica de$f(x) = x^2$. Esto es fácil de ver ya que ambas ecuaciones utilizan los mismos valores x en la tabla de la Figura$\PageIndex{10}$ (b), pero los valores de función de$g(x) = x^2 + 1$ son una unidad mayores que los valores de función correspondientes de$f(x) = x^2$.

Obsérvese que el vértice de la gráfica de también se$g(x) = x^2 + 1$ ha desplazado hacia arriba 1 unidad y ahora se ubica en el punto (0, 1).

Figura$\PageIndex{10}$: Un desplazamiento vertical o traslación.

La discusión anterior lleva a la siguiente propiedad.

Propiedad 11

Si c > 0, la gráfica de$g(x) = x^2 + c$ se desplaza c unidades hacia arriba de la gráfica de$f(x) = x^2$.

En una línea similar, la gráfica de$y = x^2 − 1$ se desplaza hacia abajo una unidad de la gráfica de$y = x^2$

Ejemplo$\PageIndex{5}$

Esboce los gráficos de$y = x^2$ y$y = x^2 − 1$ en su calculadora gráfica.

Solución

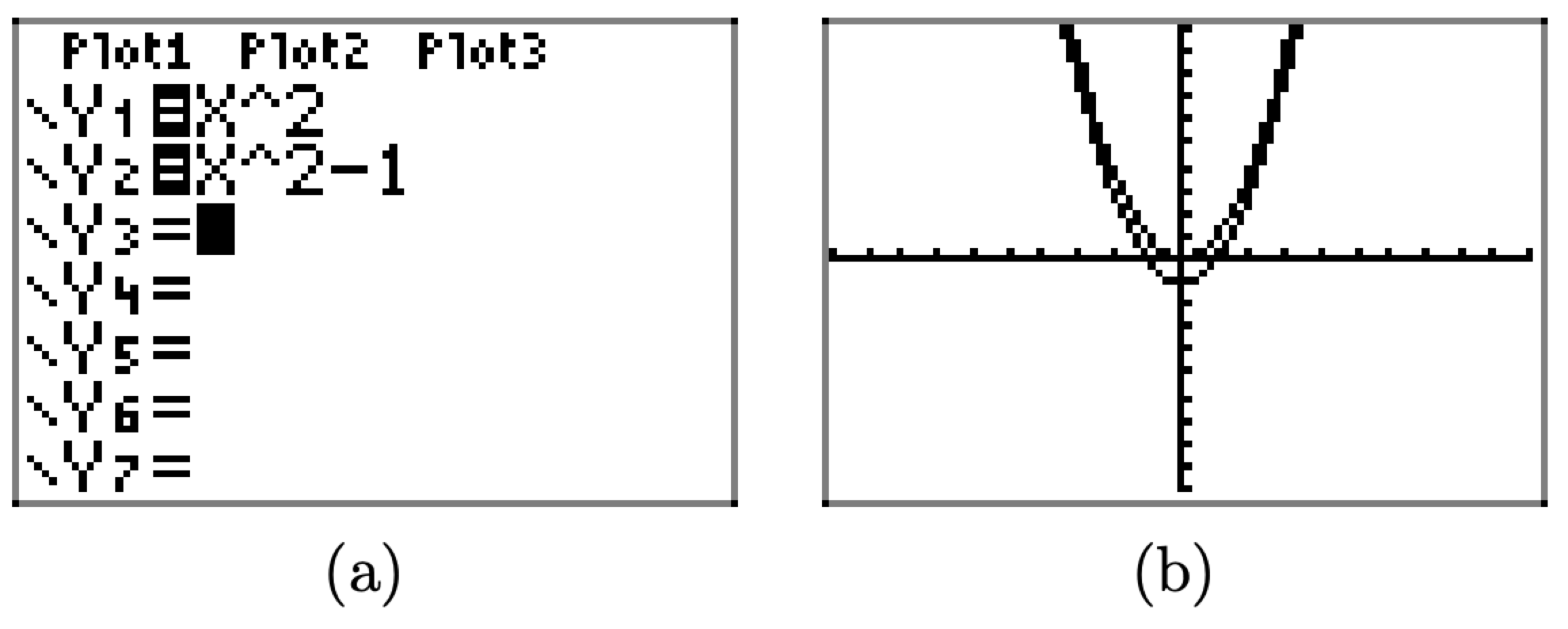
Cargue las ecuaciones$y = x^2$ y$y = x^2 − 1$ en el menú Y=, como se muestra en la Figura$\PageIndex{11}$ (a). Pulse el botón ZOOM y seleccione 6:ZStandard para producir la imagen que se muestra en la Figura$\PageIndex{11}$ (b).

Tenga en cuenta que la gráfica de$y = x^2 − 1$ se desplaza 1 unidad hacia abajo desde la gráfica de$y = x^2$ y el vértice de la gráfica de ahora$y = x^2 − 1$ está en el punto (0, −1).

Figura$\PageIndex{11}$: Dibujo$y = x^2$ y$y = x^2 − 1$ en la calculadora gráfica.

La discusión anterior lleva a la siguiente propiedad.

Propiedad 13

Si c > 0, la gráfica de$g(x) = x^2 − c$ se desplaza c unidades hacia abajo desde la gráfica de$f(x) = x^2$.

El eje de simetría

En la Figura$\PageIndex{1}$, la gráfica de$y = x^2$ es simétrica con respecto al eje y. Una mitad de la parábola es una imagen especular de la otra con respecto al eje y. Decimos que el eje y está actuando como eje de simetría.

Si la parábola se refleja a través del eje x, como en la Figura 6, el eje de simetría no cambia. La gráfica sigue siendo simétrica con respecto al eje y. Comentarios similares están en orden para escalados y traducciones verticales. Sin embargo, si la gráfica de$y = x^2$ se desplaza hacia la derecha o hacia la izquierda, entonces el eje de simetría cambiará.

Ejemplo$\PageIndex{6}$

Esbozar la gráfica de$y = −(x + 2)^2 + 3$.

Solución

Aunque no es necesario, este ejemplo es mucho más sencillo si realizas reflexiones antes de las traducciones.

Punta 15. Si es posible, realice escalados y reflexiones antes de las traducciones.

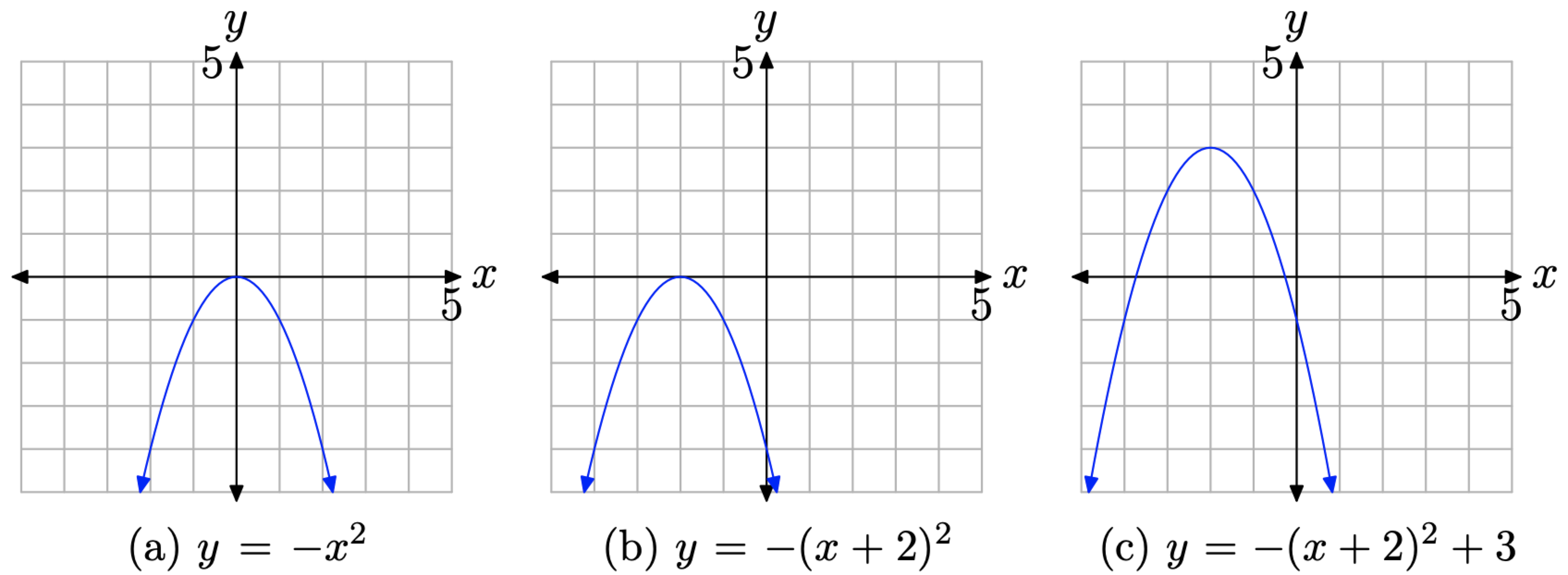
En la serie mostrada en la Figura$\PageIndex{12}$, primero realizamos una reflexión, luego una traslación horizontal, seguida de una traslación vertical.

• En la Figura$\PageIndex{12}$ (a), la gráfica de$y = −x^2$ es un reflejo de la gráfica de$y = x^2$ a través del eje x y se abre hacia abajo. Tenga en cuenta que el vértice se encuentra todavía en el origen.
• En la Figura$\PageIndex{12}$ (b), hemos reemplazado x por x+ 2 en la ecuación$y = −x^2$ para obtener la ecuación$y = −(x+ 2)^2$. El efecto es desplazar la gráfica de$y = −x^2$ la Figura$\PageIndex{12}$ (a) 2 unidades hacia la izquierda para obtener la gráfica de$y = −(x+ 2)^2$ la Figura$\PageIndex{12}$ (b). Tenga en cuenta que el vértice está ahora en el punto (−2, 0).
• En la Figura$\PageIndex{12}$ (c), hemos agregado 3 a la ecuación$y = −(x+ 2)^2$ para obtener la ecuación$y = −(x+ 2)^2 + 3$. El efecto es desplazar la gráfica de y = − (x+ 2) 2 en la Figura$\PageIndex{12}$ (b) hacia arriba 3 unidades para obtener la gráfica de$y=-(x+2)^{2}+3$ la Figura$\PageIndex{12}$ (c). Tenga en cuenta que el vértice se encuentra ahora en el punto (−2, 3).

Figura$\PageIndex{12}$: Encontrar la gráfica de$y=-(x+2)^{2}+3$ a través de una serie de transformaciones.

En la práctica, podemos proceder con mayor rapidez. Analizar la ecuación$y=-(x+2)^{2}+3$. El signo menos nos dice que la parábola “se abre hacia abajo”. La presencia de x + 2 indica un desplazamiento de 2 unidades hacia la izquierda. Por último, sumando el 3 desplazará la gráfica 3 unidades hacia arriba. Así, tenemos una parábola que “se abre hacia abajo” con vértice en (−2, 3). Esto se muestra en la Figura$\PageIndex{13}$.

Figura$\PageIndex{13}$: El eje de simetría pasa por el vértice.

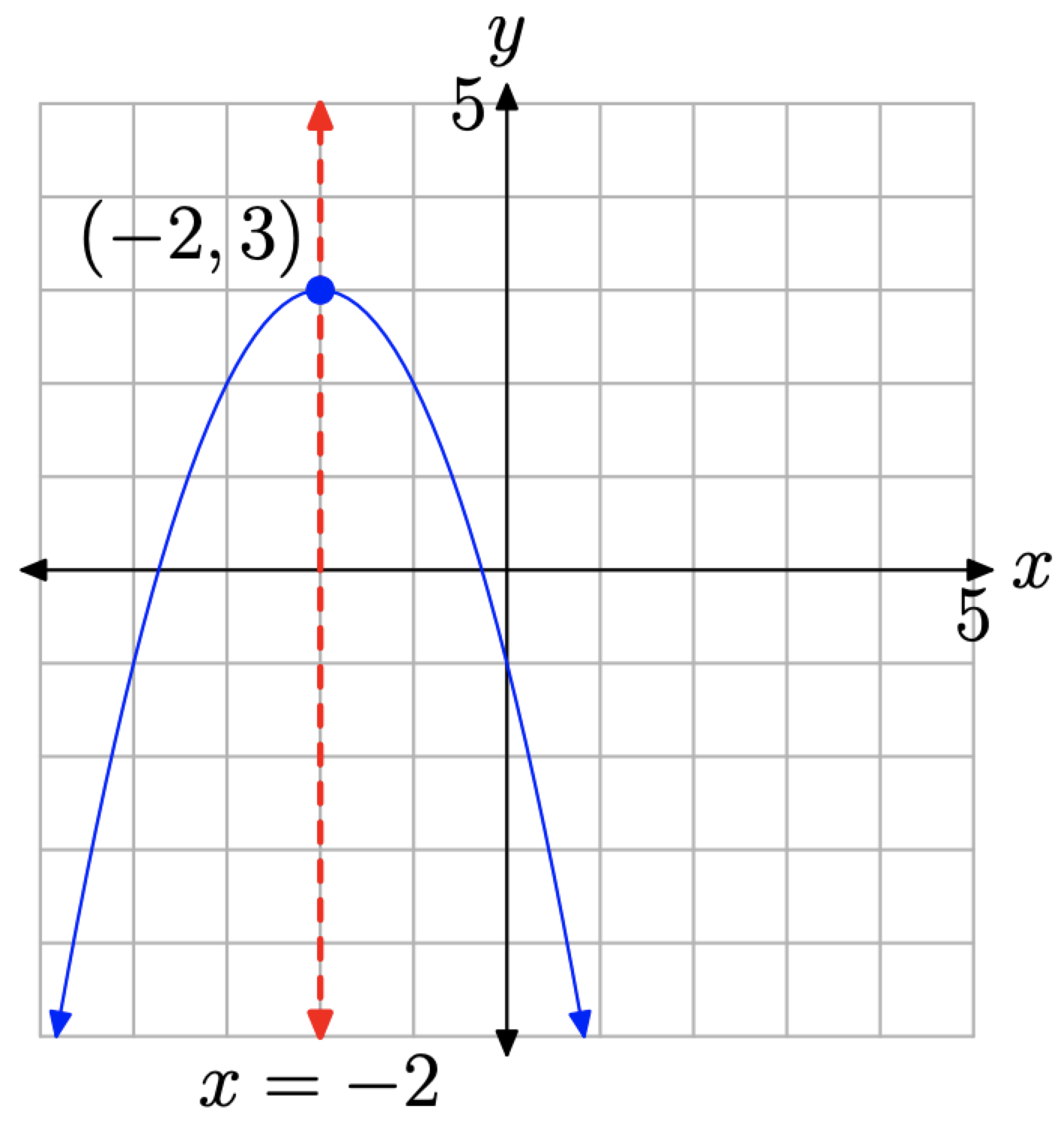
El eje de simetría pasa por el vértice (−2, 3) en la Figura$\PageIndex{13}$ y tiene la ecuación x = −2. Tenga en cuenta que la mitad derecha de la parábola es una imagen especular de su mitad izquierda a través de este eje de simetría. Podemos usar el eje de simetría para obtener una gráfica precisa de la parábola con un trazado mínimo de puntos.

Lineamientos para el Uso del Eje de Simetría

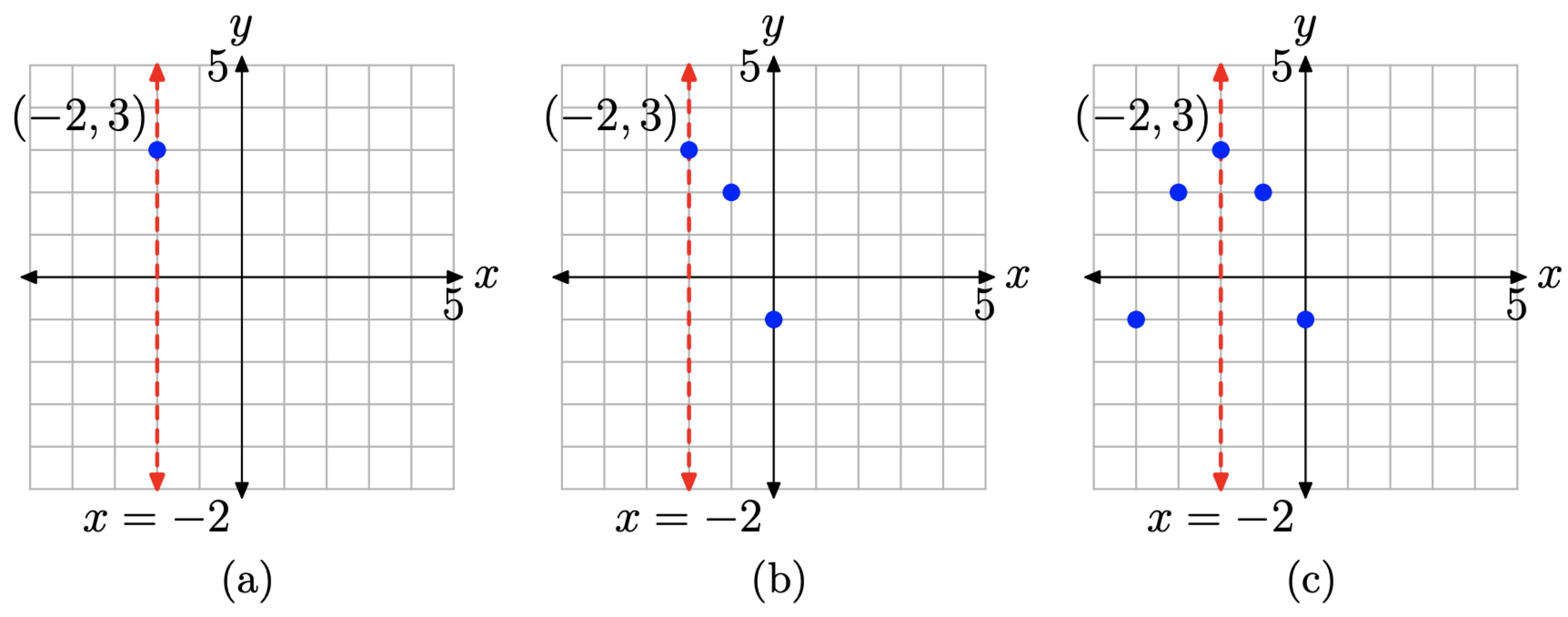
• Comience trazando el vértice y el eje de simetría como se muestra en la Figura$\PageIndex{14}$ (a).
• A continuación, computa dos puntos a cada lado del eje de simetría. Elegimos x = −1 y x = 0 y calculamos los valores y correspondientes usando la ecuación$y=-(x+2)^{2}+3$

x	$y=-(x+2)^{2}+3$
-1	\ (y=- (x+2) ^ {2} +3\) ">2
0	\ (y=- (x+2) ^ {2} +3\) ">-1

Trazar los puntos de la tabla, como se muestra en la Figura$\PageIndex{14}$ (b).

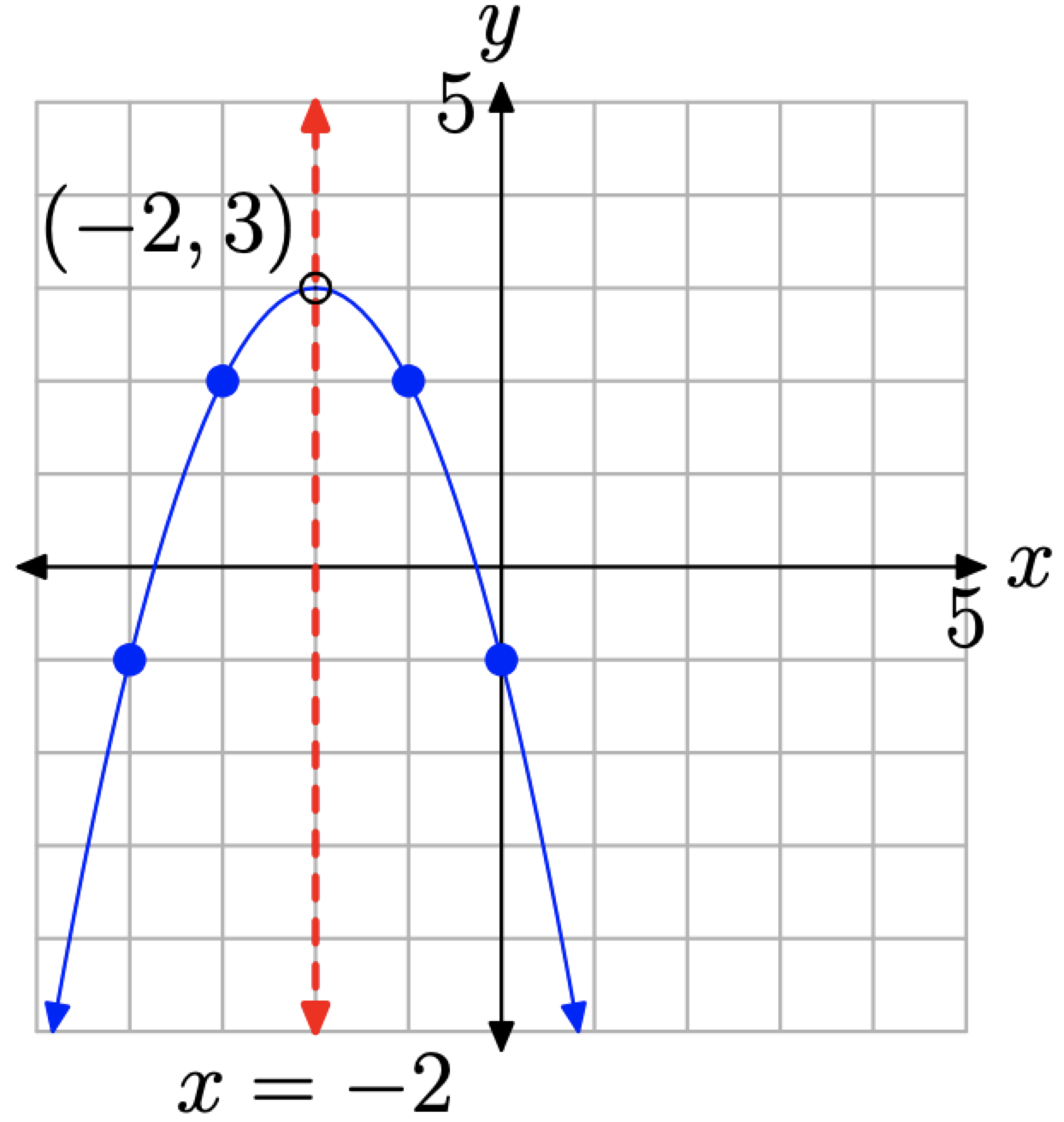
• Finalmente, graficar las imágenes especular de estos puntos a través del eje de simetría, como se muestra en la Figura$\PageIndex{14}$ (c).

Figura$\PageIndex{14}$: Usando el eje de simetría para establecer precisión.

La imagen en la Figura$\PageIndex{14}$ (c) contiene claramente suficiente información para completar la gráfica de la parábola que tiene la ecuación$y=-(x+2)^{2}+3$ en la Figura$\PageIndex{15}$.

Figura$\PageIndex{15}$: Una gráfica precisa de$y=-(x+2)^{2}+3$.

Resumamos lo que hemos visto hasta ahora.

Resumen 16

La forma de la función cuadrática $$f(x)=a(x-h)^{2}+k$$ se llama forma de vértice. La gráfica de esta función cuadrática es una parábola.

1. La gráfica de la parábola se abre hacia arriba si a > 0, hacia abajo si a < 0.
2. Si la magnitud de a es mayor que 1, entonces la gráfica de la parábola se estira por un factor de a.Si la magnitud de a es menor que 1, entonces la gráfica de la parábola se comprime por un factor de 1/a.
3. La parábola se traduce h unidades a la derecha si h > 0, y h unidades a la izquierda si h < 0.
4. La parábola se traduce k unidades hacia arriba si k > 0, y k unidades hacia abajo si k < 0.
5. Las coordenadas del vértice son (h, k).
6. El eje de simetría es una línea vertical a través del vértice cuya ecuación es x = h.

Veamos un último ejemplo

Ejemplo$\PageIndex{7}$

Utilice la técnica de Ejemplo$\PageIndex{6}$ para bosquejar la gráfica de$f(x) = 2(x − 2)^2 − 3$.

Solución

Compare$f(x) = 2(x − 2)^2 − 3$ con$f(x)=a(x-h)^{2}+k$ y tenga en cuenta que a = 2. De ahí que la parábola haya sido “estirada” por un factor de 2 y se abra hacia arriba. La presencia de x − 2 indica un desplazamiento de 2 unidades hacia la derecha; y restando 3 desplaza la parábola 3 unidades hacia abajo. Por lo tanto, el vértice se ubicará en el punto (2, −3) y el eje de simetría será la línea vertical que tiene la ecuación x = 2. Esto se muestra en la Figura$\PageIndex{16}$ (a).

Nota

Algunos prefieren una comparación más estricta$f(x) = 2(x − 2)^2 − 3$ con la forma general del vértice$f(x)=a(x-h)^{2}+k$, produciendo a = 2, h = 2 y k = −3. Esto identifica inmediatamente el vértice en (h, k), o (2, −3).

A continuación, evalúa la función$f(x) = 2(x − 2)^2 − 3$ en dos puntos que se encuentran a la derecha del eje de simetría (o a la izquierda, si lo prefieres). Debido a que el eje de simetría es la línea vertical x = 2, elegimos evaluar la función en x = 3 y 4.

$$\begin{array}{l}{f(3)=2(3-2)^{2}-3=-1} \\ {f(4)=2(4-2)^{2}-3=5}\end{array}$$

Esto nos da dos puntos a la derecha del eje de simetría, (3, −1) y (4, 5), que trazamos en la Figura$\PageIndex{16}$ (b).

Finalmente, trazamos las imágenes especulares de (3, −1) y (4, 5) a través del eje de simetría, lo que nos da los puntos (1, −1) y (0, 5), respectivamente. Estos se trazan en la Figura$\PageIndex{16}$ (c). Después dibujamos la parábola a través de estos puntos.

Figura$\PageIndex{16}$: Creando la gráfica de$f(x) = 2(x − 2)^2 − 3$.

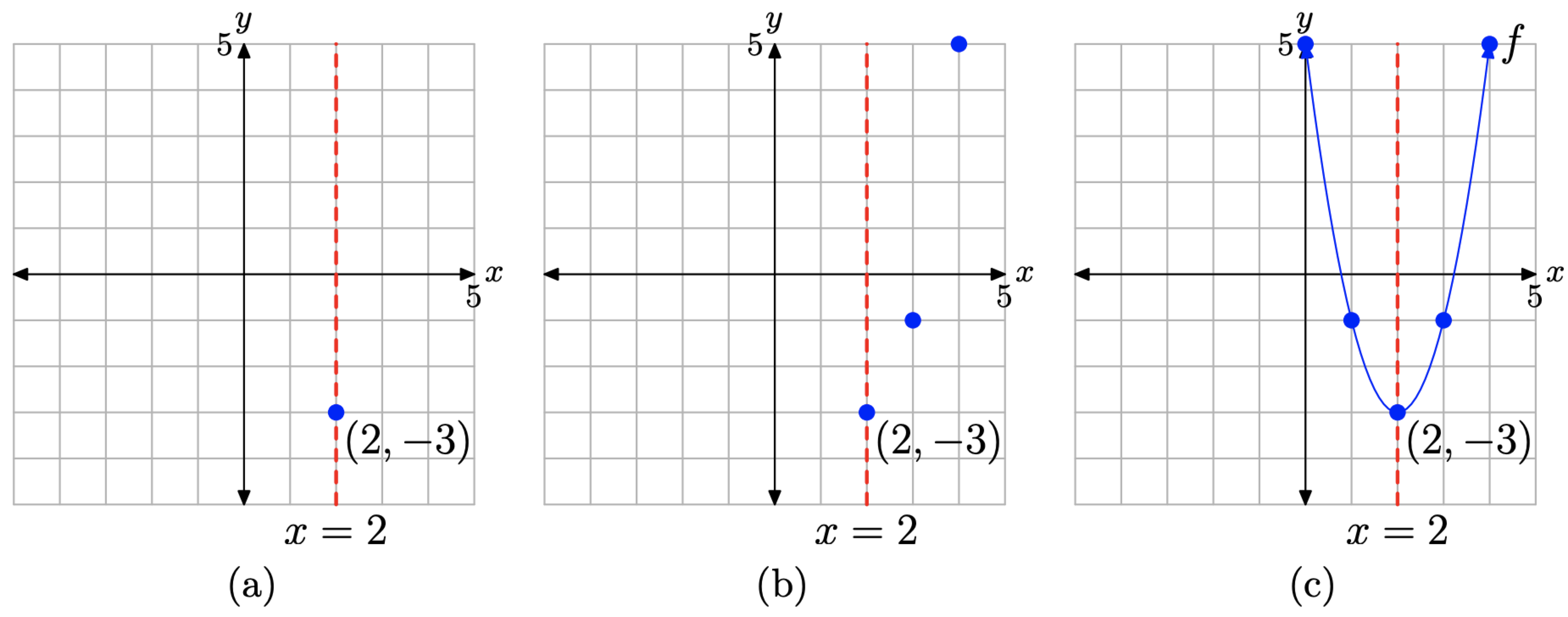
Terminemos describiendo el dominio y el rango de la función definida por la regla$f(x)=2(x-2)^{2}-3$. Si usa la noción intuitiva de que el dominio es el conjunto de “valores x permisibles”, entonces uno puede sustituir cualquier número que desee en la ecuación$f(x)=2(x-2)^{2}-3$. Por lo tanto, el dominio es todo números reales, que podemos escribir de la siguiente manera: Domain =$\mathbb{R}$ o Domain =$(-\infty, \infty)$.

También puede proyectar cada punto en la gráfica de$f(x)=2(x-2)^{2}-3$ sobre el eje x, como se muestra en la Figura$\PageIndex{17}$ (a). Si haces esto, entonces todo el eje “quedará en la sombra”, así que una vez más, el dominio es todo números reales.

Figura$\PageIndex{17}$: Proyectando para encontrar (a) el dominio y (b) el rango.

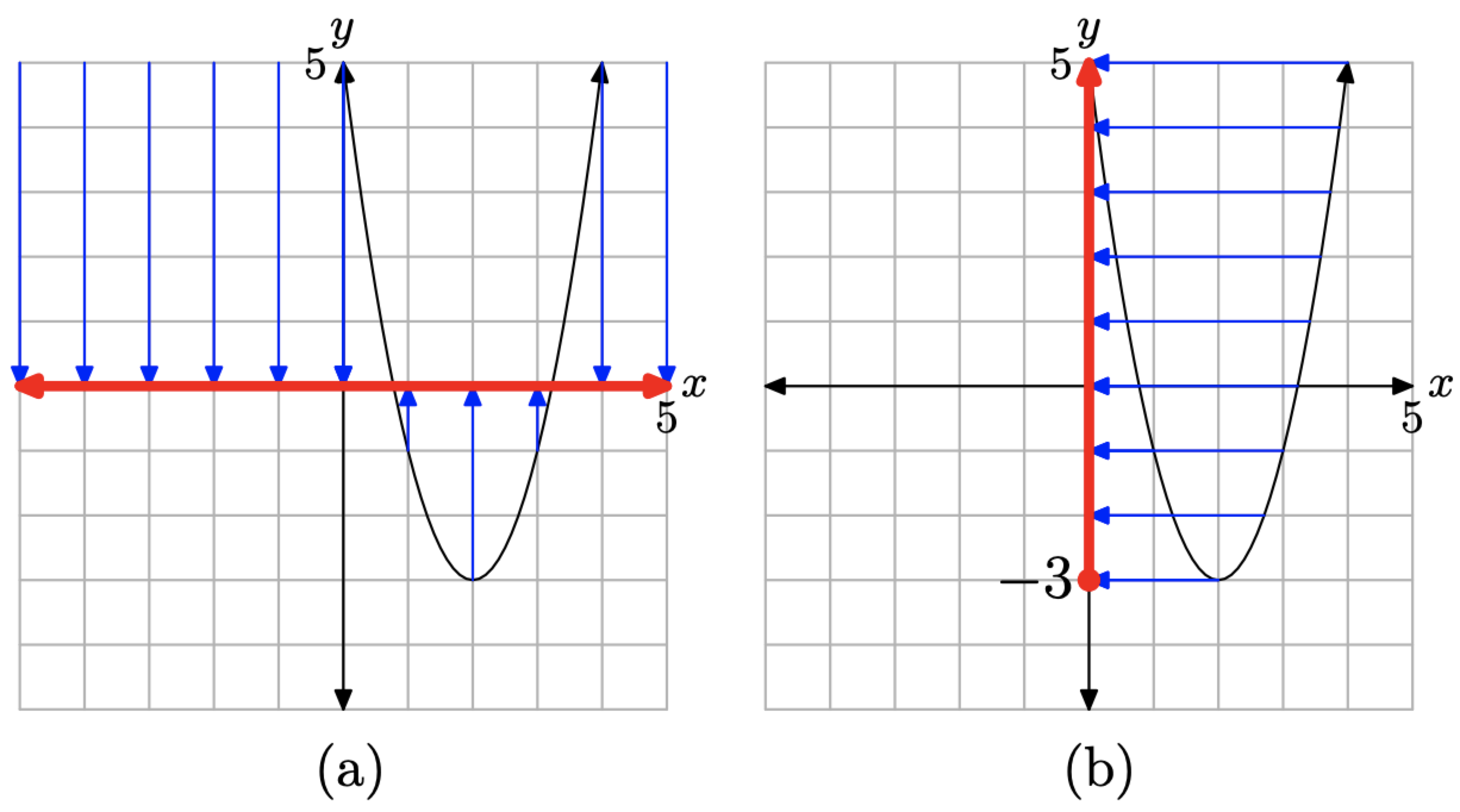
Para determinar el rango de la función$f(x)=2(x-2)^{2}-3$, proyecte cada punto de la gráfica de f sobre el eje y, como se muestra en la Figura$\PageIndex{17}$ (b). En el eje y, todos los puntos mayores o iguales a −3 “se encuentran en sombra”, por lo que el rango se describe con Rango$=\{y : y \geq-3\}=[-3, \infty)$.

A continuación se resume cómo se encuentra el dominio y el rango de una función cuadrática que está en forma de vértice.

Resumen 18

El dominio de la función cuadrática $$f(x)=a(x-h)^{2}+k$$ , independientemente de los valores de los parámetros a, h y k, es el conjunto de todos los números reales, fácilmente descritos con$\mathbb{R}$ o$(-\infty, \infty)$. Por otro lado, el rango depende de los valores de a y k.

• Si a > 0, entonces la parábola se abre hacia arriba y tiene vértice en (h, k). En consecuencia, el rango será $$[k, \infty)=\{y : y \geq k\}$$ .
• Si a < 0, entonces la parábola se abre hacia abajo y tiene vértice en (h, k). En consecuencia, el rango será $$(-\infty, k]=\{y : y \leq k\}$$ .

Ejercicio

En Ejercicios 1 - 6, dibuja la imagen de la pantalla de tu calculadora en tu papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Etiquete cada gráfica con su ecuación. Recuerda usar una regla para dibujar todas las líneas, incluidos los ejes.

Ejercicio$\PageIndex{1}$

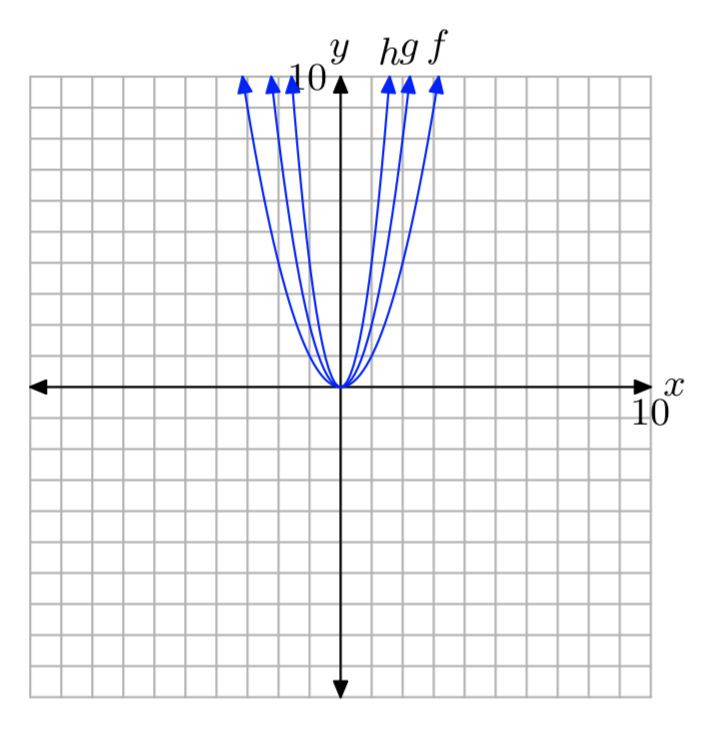
Usa tu calculadora gráfica para bosquejar los gráficos de$f(x) = x^2$$g(x) = 2x^2$, y$h(x) = 4x^2$ en una pantalla. Escribe una breve oración explicando lo que aprendiste en este ejercicio.

Contestar

Multiplicando por 2 escalas verticalmente por un factor de 2. Multiplicando por 4 escalas verticalmente por un factor de 4.

Ejercicio$\PageIndex{2}$

Usa tu calculadora gráfica para bosquejar los gráficos de$f(x) = −x^2$$g(x) = −2x^2$, y$h(x) = −4x^2$ en una pantalla. Escribe una breve oración explicando lo que aprendiste en este ejercicio.

Ejercicio$\PageIndex{3}$

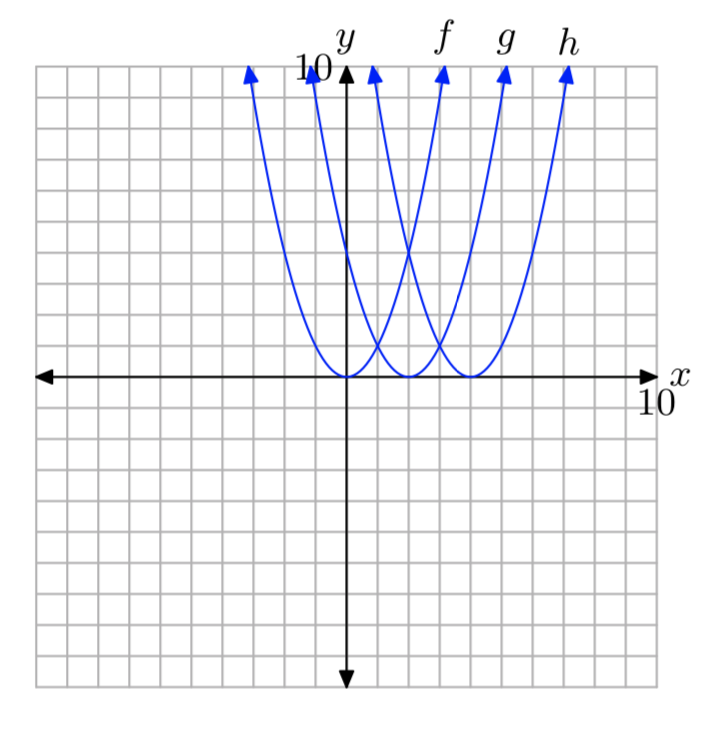
Usa tu calculadora gráfica para bosquejar los gráficos de$f(x) = x^2$$g(x) = (x−2)^2$, y$h(x) = (x−4)^2$ en una pantalla. Escribe una breve oración explicando lo que aprendiste en este ejercicio.

Contestar

La gráfica de$g(x) = (x−2)^2$ se desplaza 2 unidades a la derecha de$f(x) = x^2$. La gráfica de$h(x) = (x−4)^2$ se desplaza 4 unidades a la derecha de$f(x) = x^2$.

Ejercicio$\PageIndex{4}$

Usa tu calculadora gráfica para bosquejar los gráficos de$f(x) = x^2$$g(x) = (x+2)^2$, y$h(x) = (x+4)^2$ en una pantalla. Escribe una breve oración explicando lo que aprendiste en este ejercicio.

Ejercicio$\PageIndex{5}$

Usa tu calculadora gráfica para bosquejar los gráficos de$f(x) = x^2$$g(x) = x^2+2$, y$h(x) = x^2+4$ en una pantalla. Escribe una breve oración explicando lo que aprendiste en este ejercicio.

Contestar

La gráfica de$g(x) = x^2+2$ se desplaza 2 unidades hacia arriba desde la gráfica de$f(x) = x^2$ .La gráfica de$h(x) = x^2+4$ se desplaza 4 unidades hacia arriba de la gráfica de$f(x) = x^2$.

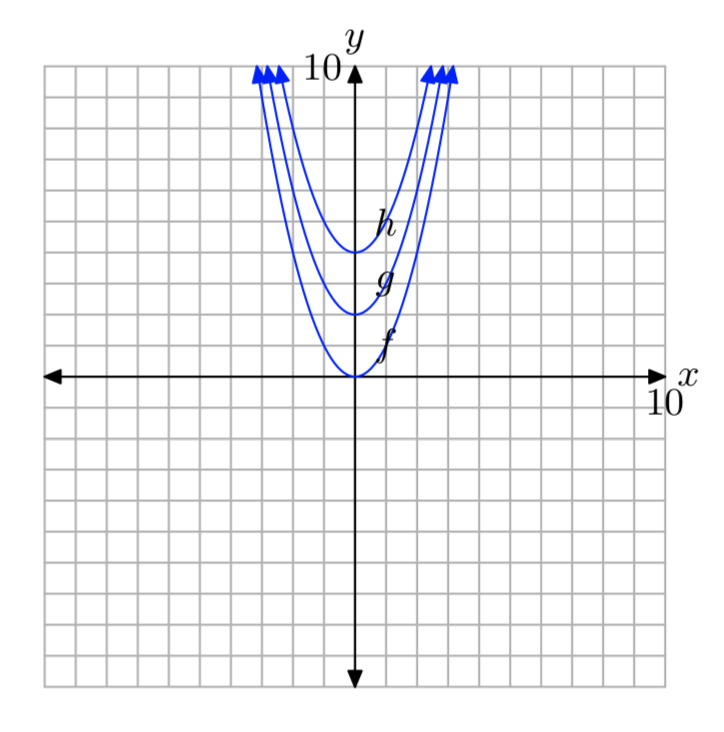
Ejercicio$\PageIndex{6}$

Usa tu calculadora gráfica para bosquejar los gráficos de$f(x) = x^2$$g(x) = x^2−2$, y$h(x) = x^2−4$ en una pantalla. Escribe una breve oración explicando lo que aprendiste en este ejercicio.

En los Ejercicios 7 - 14, anota la función cuadrática dada en tu trabajo de tarea, luego indica las coordenadas del vértice.

Ejercicio$\PageIndex{7}$

$f(x) = −5(x−4)^2−5$

Contestar

(4, −5)

Ejercicio$\PageIndex{8}$

$f(x) = 5(x+3)^2−7$

Ejercicio$\PageIndex{9}$

$f(x) = 3(x+1)^2$

Contestar

(− 1, 0)

Ejercicio$\PageIndex{10}$

$f(x) = \frac{7}{5}(x+\frac{5}{9})^2−\frac{3}{4}$

Ejercicio$\PageIndex{11}$

$f(x) = −7(x−4)^2+6$

Contestar

(4, 6)

Ejercicio$\PageIndex{12}$

$f(x) = −\frac{1}{2}(x−\frac{8}{9})^2+\frac{2}{9}$

Ejercicio$\PageIndex{13}$

$f(x) = \frac{1}{6}(x+\frac{7}{3})^2+\frac{3}{8}$

Contestar

$(−\frac{7}{3}, \frac{3}{8})$

Ejercicio$\PageIndex{14}$

$f(x) = −\frac{3}{2}(x+\frac{1}{2})^2−\frac{8}{9}$

En los Ejercicios 15 - 22, exponer la ecuación del eje de simetría de la gráfica de la función cuadrática dada.

Ejercicio$\PageIndex{15}$

$f(x) = −7(x−3)^2+1$

Contestar

x = 3

Ejercicio$\PageIndex{16}$

$f(x) = −6(x+8)^2+1$

Ejercicio$\PageIndex{17}$

$f(x) = −\frac{7}{8}(x+\frac{1}{4})^2+\frac{2}{3}$

Contestar

$x = −\frac{1}{4}$

Ejercicio$\PageIndex{18}$

$f(x) = −\frac{1}{2}(x−\frac{3}{8})^2−\frac{5}{7}$

Ejercicio$\PageIndex{19}$

$f(x) = −\frac{2}{9}(x+\frac{2}{3})^2−\frac{4}{5}$

Contestar

$x = −\frac{2}{3}$

Ejercicio$\PageIndex{20}$

$f(x) = −7(x+3)^2+9$

Ejercicio$\PageIndex{21}$

$f(x) = −\frac{8}{7}(x+\frac{2}{9})^2+\frac{6}{5}$

Contestar

$x = −\frac{2}{9}$

Ejercicio$\PageIndex{22}$

$f(x) = 3(x+3)^2+6$

En los Ejercicios 23 - 36, realice cada una de las siguientes tareas para la función cuadrática dada.

1. Configure un sistema de coordenadas en papel cuadriculado. Etiquetar y escalar cada eje.
2. Trazar el vértice de la parábola y etiquetarlo con sus coordenadas.
3. Dibuja el eje de simetría y etiquétalo con su ecuación.
4. Configure una tabla cerca de su sistema de coordenadas que contenga coordenadas exactas de dos puntos a cada lado del eje de simetría. Trócalos en tu sistema de coordenadas y sus “imágenes espejo” a través del eje de simetría.
5. Dibuja la parábola y etiquétalo con su ecuación.
6. Utilice la notación de intervalos para describir tanto el dominio como el rango de la función cuadrática.

Ejercicio$\PageIndex{23}$

$f(x) = (x+2)^2−3$

Contestar

Dominio=$(−\infty, \infty)$; Intervalo = [−3,$\infty$)

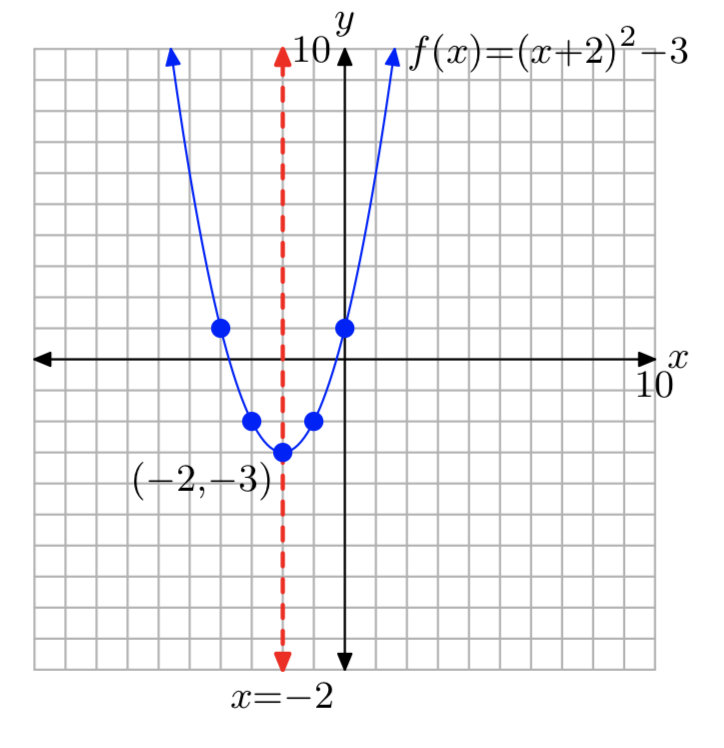
Ejercicio$\PageIndex{24}$

$f(x) = (x−3)^2−4$

Ejercicio$\PageIndex{25}$

$f(x) = −(x−2)^2+5$

Contestar

Dominio=$(−\infty, \infty)$; Intervalo = (−$\infty$, 5]

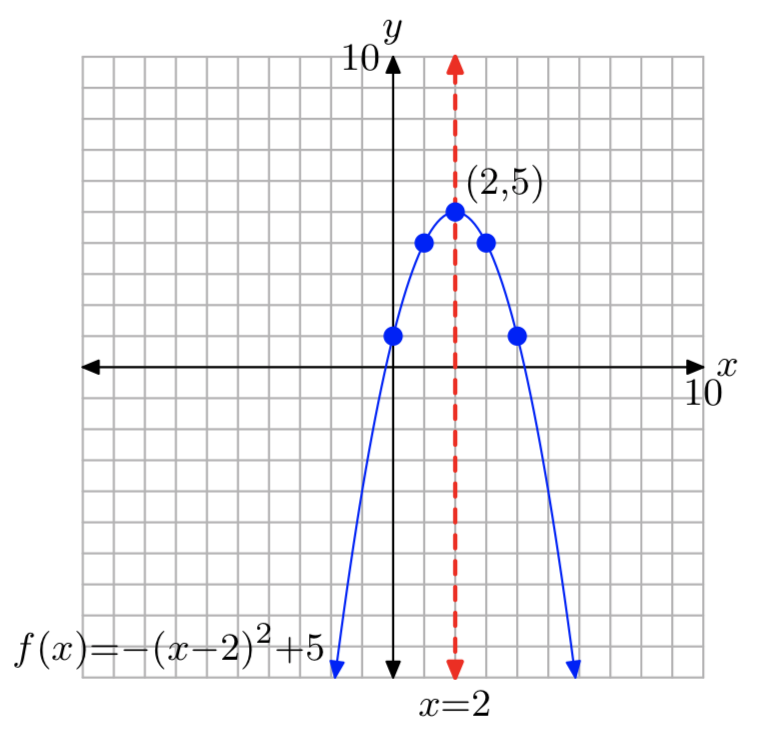
Ejercicio$\PageIndex{26}$

$f(x) = −(x+4)^2+4$

Ejercicio$\PageIndex{27}$

$f(x) = (x−3)^2$

Contestar

Dominio=$(−\infty, \infty)$; Intervalo = [0,$\infty$)

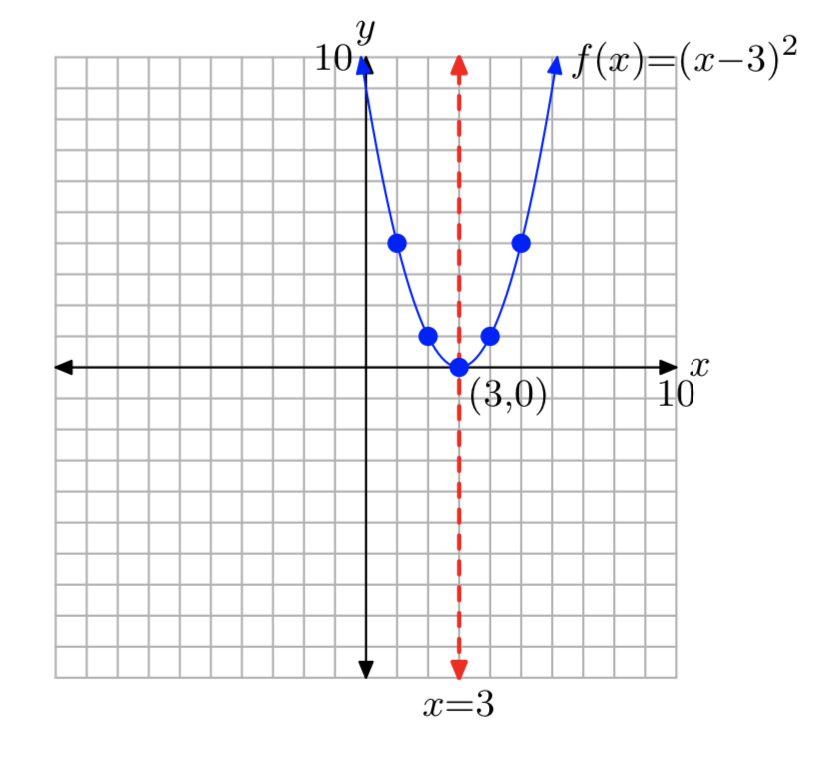
Ejercicio$\PageIndex{28}$

$f(x) = −(x+2)^2$

Ejercicio$\PageIndex{29}$

$f(x) = −x^2+7$

Contestar

Dominio=$(−\infty, \infty)$; Intervalo = (−$\infty$, 7]

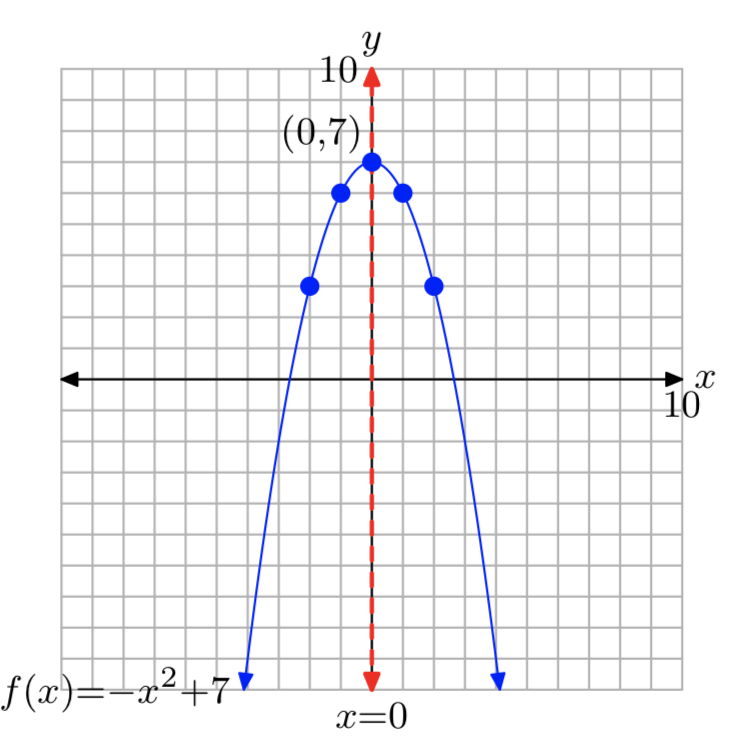
Ejercicio$\PageIndex{30}$

$f(x) = −x^2+7$

Ejercicio$\PageIndex{31}$

$f(x) = 2(x−1)^2−6$

Contestar

Dominio=$(−\infty, \infty)$; Intervalo = [−6,$\infty$)

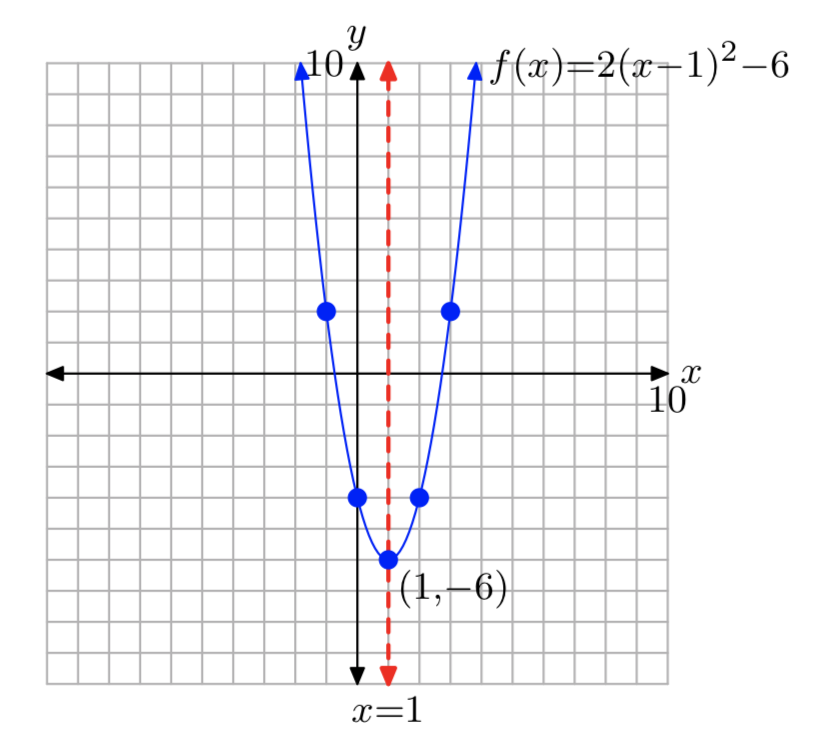
Ejercicio$\PageIndex{32}$

$f(x) = −2(x+1)^2+5$

Ejercicio$\PageIndex{33}$

$f(x) = −\frac{1}{2}(x+1)^2+5$

Contestar

Dominio=$(−\infty, \infty)$; Intervalo = (−$\infty$, 5]

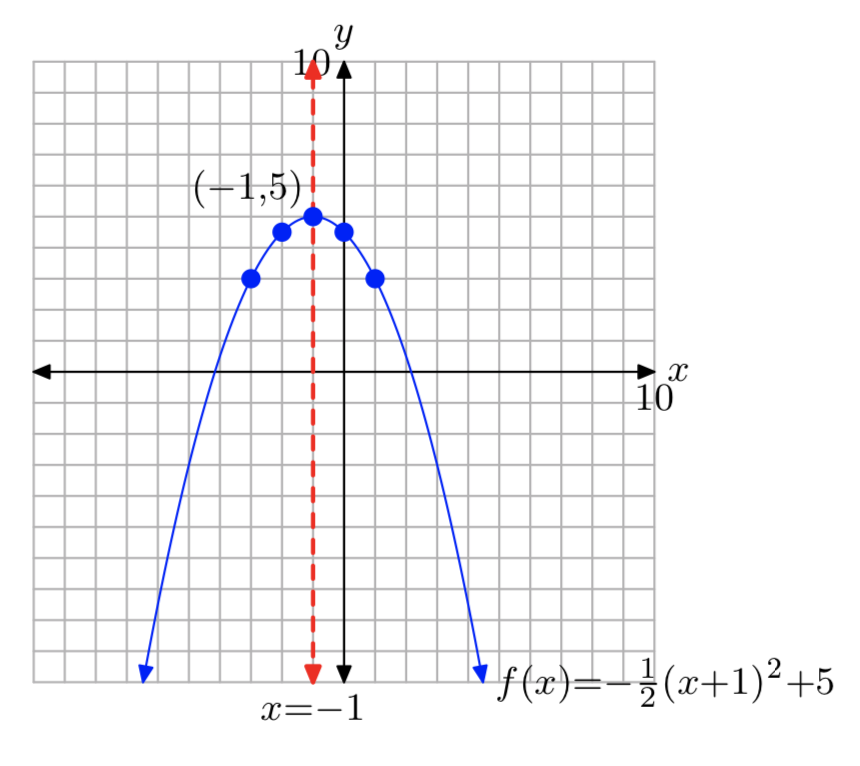
Ejercicio$\PageIndex{34}$

$f(x) = \frac{1}{2}(x−3)^2−6$

Ejercicio$\PageIndex{35}$

$f(x) = 2(x−\frac{5}{2})^2−\frac{15}{2}$

Contestar

Dominio=$(−\infty, \infty)$; Intervalo = [−$\frac{15}{2}$,$\infty$)

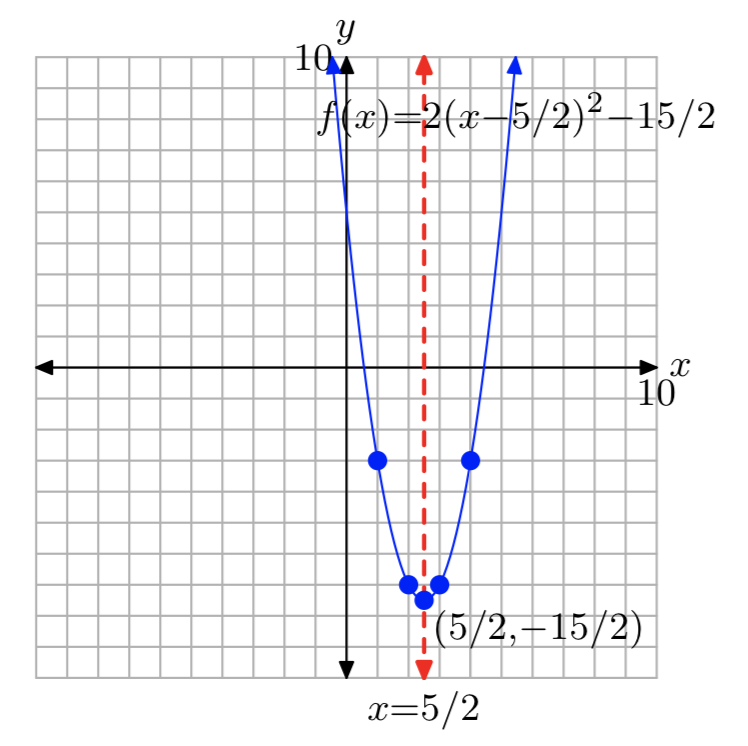
Ejercicio$\PageIndex{36}$

$f(x) = −3(x+\frac{7}{2})^2+\frac{15}{4}$

En Ejercicios 37 - 44, escribe la función cuadrática dada en tu papel de tarea, luego usa set-builder y notación de intervalo para describir el dominio y el rango de la función.

Ejercicio$\PageIndex{37}$

$f(x) = 7(x+6)^2−6$

Contestar

Dominio=$(−\infty, \infty)$; Rango = [−6,$\infty$) = {y:$y \ge −6$}

Ejercicio$\PageIndex{38}$

$f(x) = 8(x+1)^2+7$

Ejercicio$\PageIndex{39}$

$f(x) = −3(x+4)^2−7$

Contestar

Dominio=$(−\infty, \infty)$; Rango = (−$\infty$, −7] = {y:$y \le −7$}

Ejercicio$\PageIndex{40}$

$f(x) = −6(x−7)^2+9$

Ejercicio$\PageIndex{41}$

$f(x) = −7(x+5)^2−7$

Contestar

Dominio=$(−\infty, \infty)$; Rango = (−$\infty$, −7] = {y:$y \le −7$}

Ejercicio$\PageIndex{42}$

$f(x) = 8(x−4)^2+3$

Ejercicio$\PageIndex{43}$

$f(x) = −4(x−1)^2+2$

Contestar

Dominio=$(−\infty, \infty)$; Rango = (−$\infty$, 2] = {y:$y \le 2$}

Ejercicio$\PageIndex{44}$

$f(x) = 7(x−2)^2−3$

En los Ejercicios 45 - 52, utilizando el valor dado de a, encuentra la función cuadrática específica de la forma$f(x) = a(x−h)^2+k$ que tiene la gráfica mostrada. Nota: h y k son números enteros. Consulta tu solución con tu calculadora gráfica.

Ejercicio$\PageIndex{45}$

a = −2

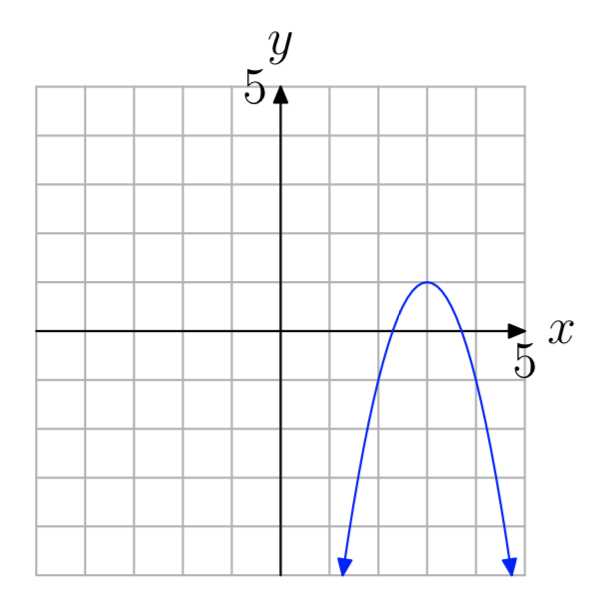
Contestar

$f(x) = −2(x−3)^2+1$

Ejercicio$\PageIndex{46}$

a = 0.5

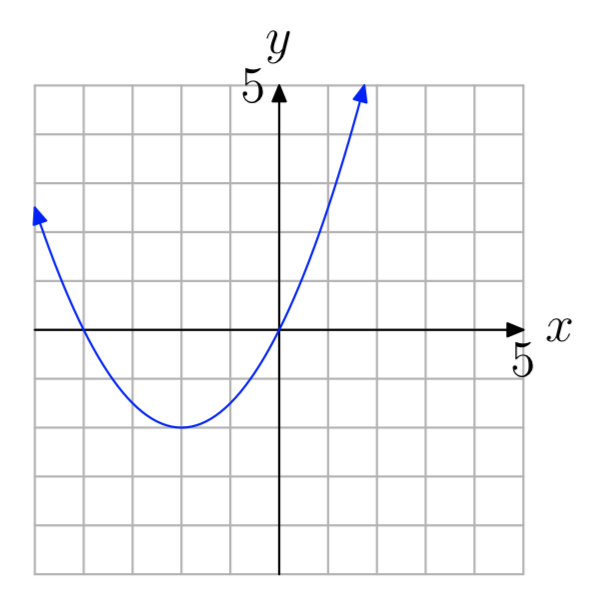
Ejercicio$\PageIndex{47}$

a = 2

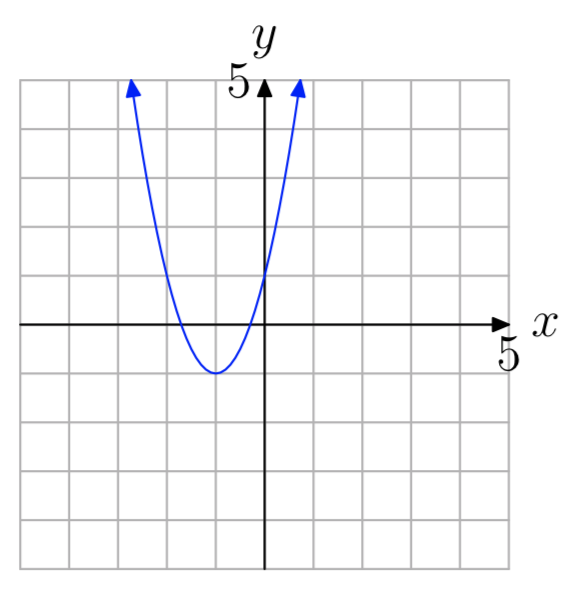
Contestar

$f(x) = 2(x+1)^2−1$

Ejercicio$\PageIndex{48}$

a = 0.5

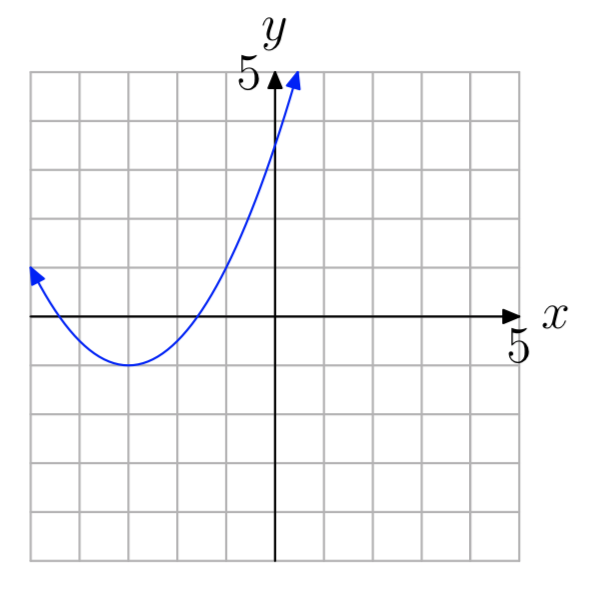
Ejercicio$\PageIndex{49}$

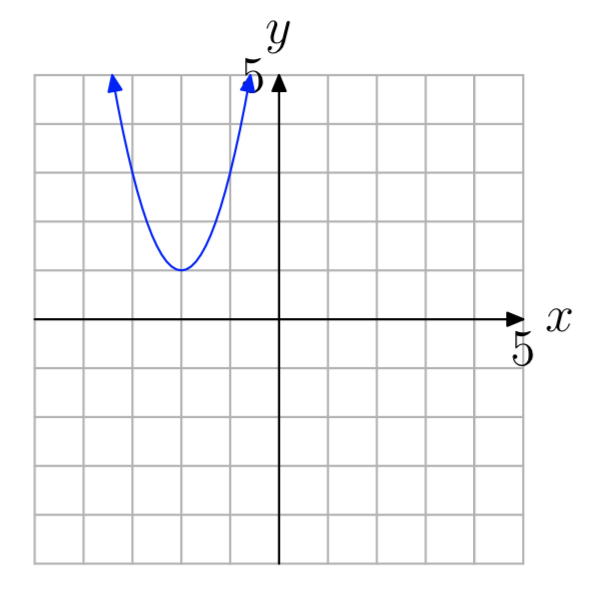
Contestar

$f(x) = 2(x+2)^2+1$

Ejercicio$\PageIndex{50}$

a = −0.5

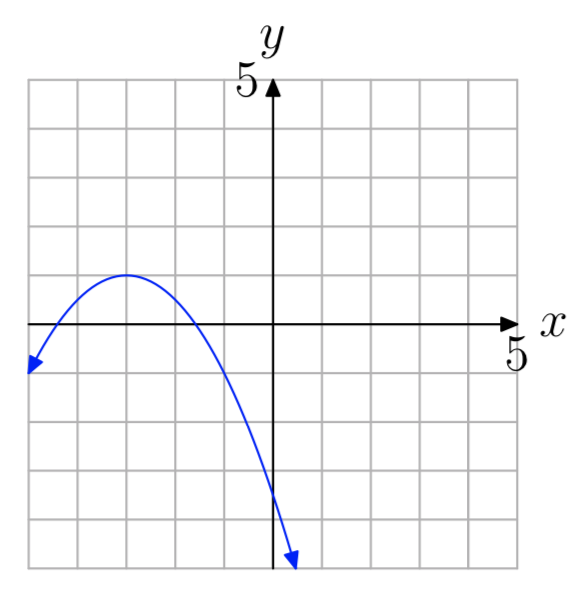
Ejercicio$\PageIndex{51}$

a = 2

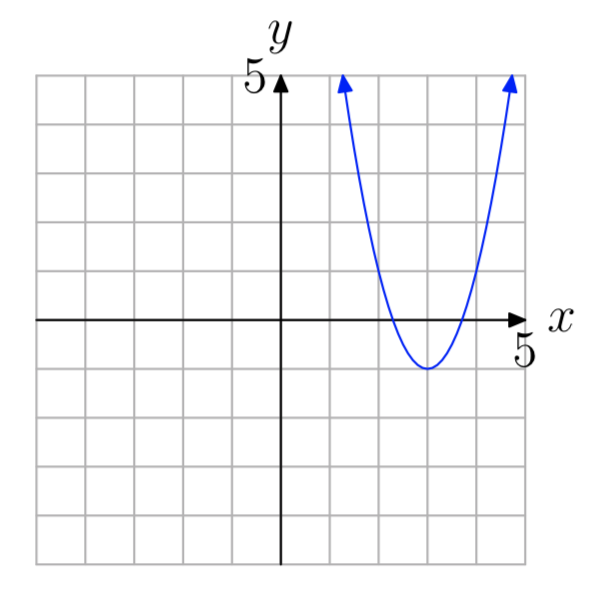
Contestar

$f(x) = 2(x−3)^2−1$

Ejercicio$\PageIndex{52}$

a = 0.5

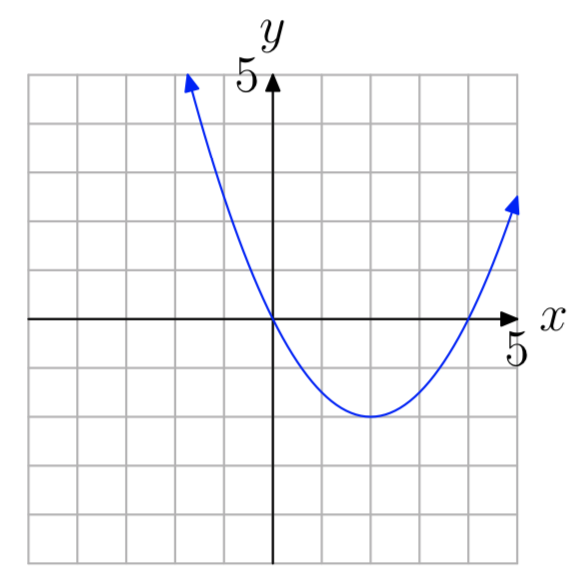
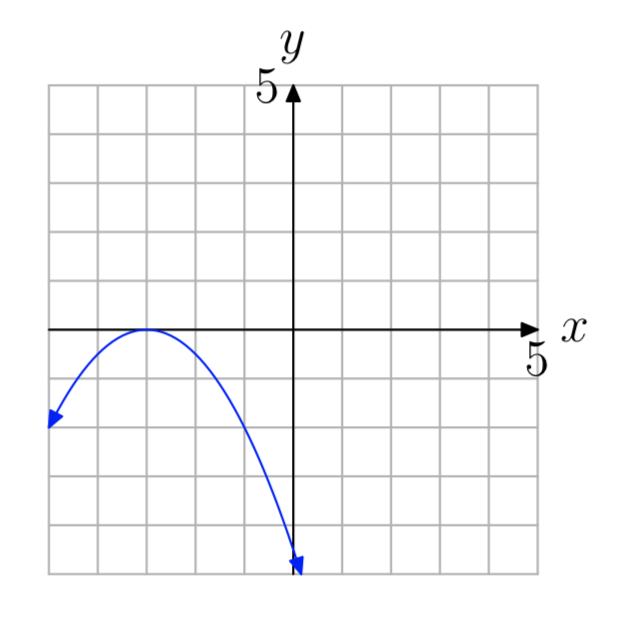
En los Ejercicios 53 - 54, usa la gráfica para determinar el rango de la función$f(x) = ax^2+bx+c$ Las flechas en la gráfica están destinadas a indicar que la gráfica continúa indefinidamente en el patrón continuo y dirección de cada flecha. Describe tu solución usando la notación de intervalos.

Ejercicio$\PageIndex{53}$

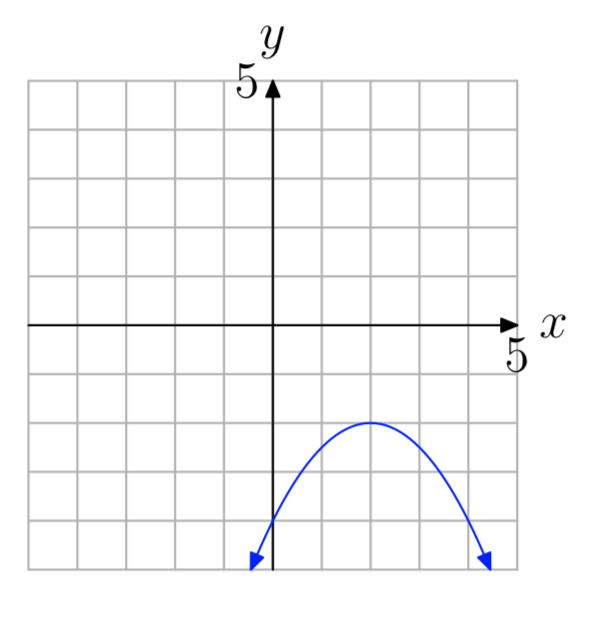
Contestar

($−\infty$, −2]

Ejercicio$\PageIndex{54}$

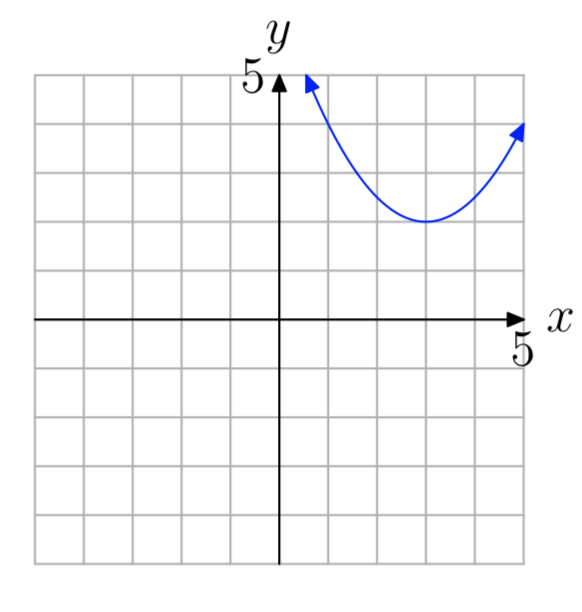
En los Ejercicios 55 - 56, utilice la gráfica para determinar el dominio de la función$f(x) = ax^2+bx+c$. Las flechas en la gráfica están destinadas a indicar que la gráfica continúa indefinidamente en el patrón continuo y dirección de cada flecha. Utilice la notación de intervalos para describir su solución.

Ejercicio$\PageIndex{55}$

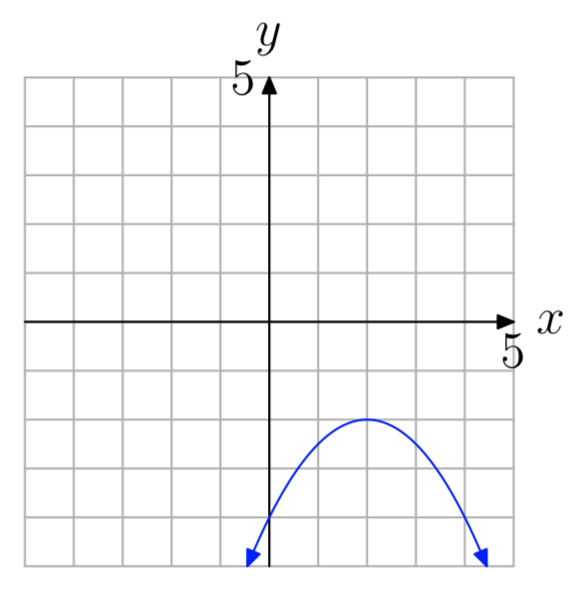
Contestar

$(−\infty, \infty)$

Ejercicio$\PageIndex{56}$