8.1: Exponentes y Raíces

Antes de definir la siguiente familia de funciones, las funciones exponenciales, tendremos que discutir en detalle la notación exponencial. Como veremos, los exponentes pueden utilizarse para describir no sólo los poderes (como\(5^2\) y\(2^3\)), sino también las raíces (como las raíces cuadradas\(\sqrt{2}\) -y las raíces\(\sqrt[3]{2}\) cubicas-). En el camino, definiremos raíces superiores y desarrollaremos algunas de sus propiedades. Un trabajo más detallado con raíces se retomará entonces en el próximo capítulo.

Exponentes enteros

Recordemos que el uso de un exponente entero positivo es simplemente una taquigrafía para la multiplicación repetida. Por ejemplo,

\[5^2 = 5 \cdot 5 \label{1}\]

y

\[2^3 = 2 \cdot 2 \cdot 2. \label{2}\]

En general,\(b^n\) representa la cantidad\(b\) multiplicada por sí misma\(n\) veces. Con esta definición, se mantienen las siguientes Leyes de Exponentes.

Leyes de los exponentes

1. \(b^{r}b^s = b^{r+s}\)
2. \(\frac{b^r}{b^s} = b^{r−s}\)
3. \((b^r)^s=b^{rs}\)

Las Leyes de los Exponentes se ilustran con los siguientes ejemplos.

Ejemplo\(\PageIndex{3}\)

1. \(2^{3}2^2 = (2 \cdot 2 \cdot 2)(2 \cdot 2) = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 2^5 = 2^{3+2}\)
2. \(\frac{2^4}{2^2} = \frac{2 \cdot 2 \cdot 2 \cdot 2}{2 \cdot 2} = 2 \cdot 2 =2^2 = 2^{4−2}\)
3. \((2^3)^2 = (2^3)(2^3) = (2 \cdot 2 \cdot 2)(2 \cdot 2 \cdot 2) = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 2^6 = 2^{3 \cdot 2}\)

Obsérvese que la segunda ley sólo tiene sentido para\(r > s\), ya que de lo contrario el exponente\(r − s\) sería negativo o 0. Pero en realidad, resulta que podemos crear definiciones para exponentes negativos y el exponente 0, y consecuentemente eliminar esta restricción.

Los exponentes negativos, así como el exponente 0, se definen simplemente de tal manera que las Leyes de los Exponentes funcionarán para todos los exponentes enteros.

• Para el exponente 0, la primera ley implica eso\(b^{0}b^1 = b^{0+1}\), y por lo tanto\(b^{0}b = b\). Si\(b \ne 0\), podemos dividir ambos lados por\(b\) para obtener\(b^{0} = 1\) (hay una excepción: no\(0^0\) está definida).
• Para los exponentes negativos, la segunda ley implica que\[b^{−n} = b^{0−n} = \frac{b^0}{b^n} = \frac{1}{b^n}\]

siempre que\(b \ne 0\). Por ejemplo,\(2^{−3} = \frac{1}{2^3} = \frac{1}{8}\), y\(2^{−4} = \frac{1}{2^4} = \frac{1}{16}\). Por lo tanto, los exponentes negativos y el exponente 0 se definen de la siguiente manera:

Definición\(\PageIndex{4}\)

\(b^{−n} = \frac{1}{b^n}\)y\(b^0 = 1\)

siempre que\(b \ne 0\).

Ejemplo\(\PageIndex{5}\)

a)\(4^{−3} = \frac{1}{4^3} = \frac{1}{64}\)

b)\(6^0 = 1\)

c)\((\frac{1}{5})^{−2} = \frac{1}{(\frac{1}{5})^2} = \frac{1}{\frac{1}{25}} = 25\)

Ahora hemos\(b^n\) definido para todos los enteros n, de tal manera que las Leyes de los Exponentes sostienen. Puede ser sorprendente saber que también podemos definir expresiones utilizando exponentes racionales, como\(2^{\frac{1}{3}}\), de manera consistente. Antes de hacerlo, sin embargo, tendremos que tomar un desvío y definir raíces.

Raíces

Raíces cuadradas: Empecemos definiendo la raíz cuadrada de un número real. Hemos utilizado la raíz cuadrada en muchas secciones de este texto, por lo que debería ser un concepto familiar. Sin embargo, en esta sección veremos las raíces cuadradas con más detalle.

Definición\(\PageIndex{6}\)

Dado un número real a, una “raíz cuadrada de a” es un número x tal que\(x^2 = a\).

Por ejemplo, 3 es una raíz cuadrada de 9 ya que\(3^2 = 9\). Likewise, − 4 es una raíz cuadrada de 16 desde entonces\((−4)^2 = 16\). En cierto sentido, tomar una raíz cuadrada es lo “opuesto” de la cuadratura, por lo que la definición de raíz cuadrada debe estar íntimamente conectada con la gráfica de\(y = x^2\), the squaring function. We investigate square roots in more detail by looking for solutions of the equation

\(x^2 = a\). (7)

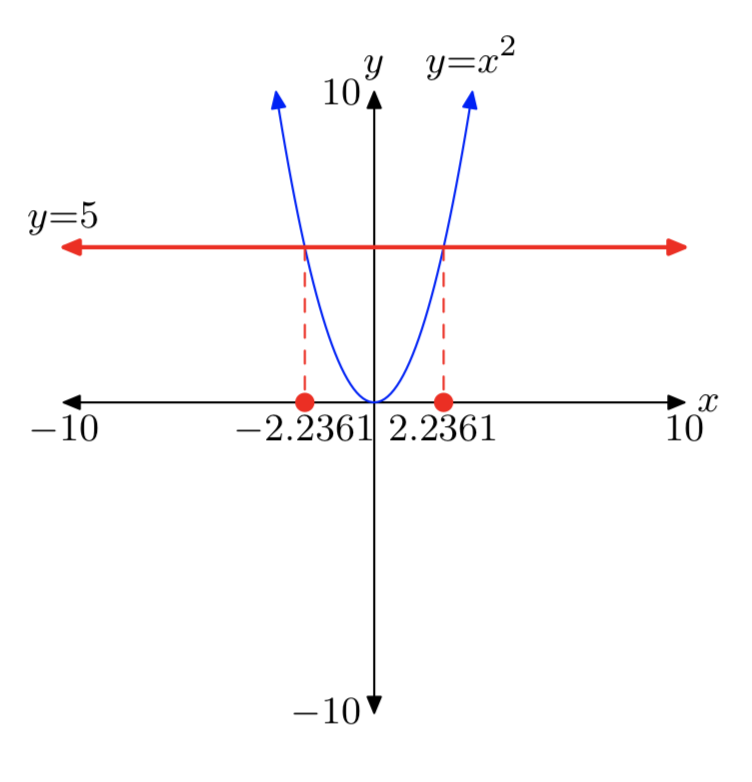
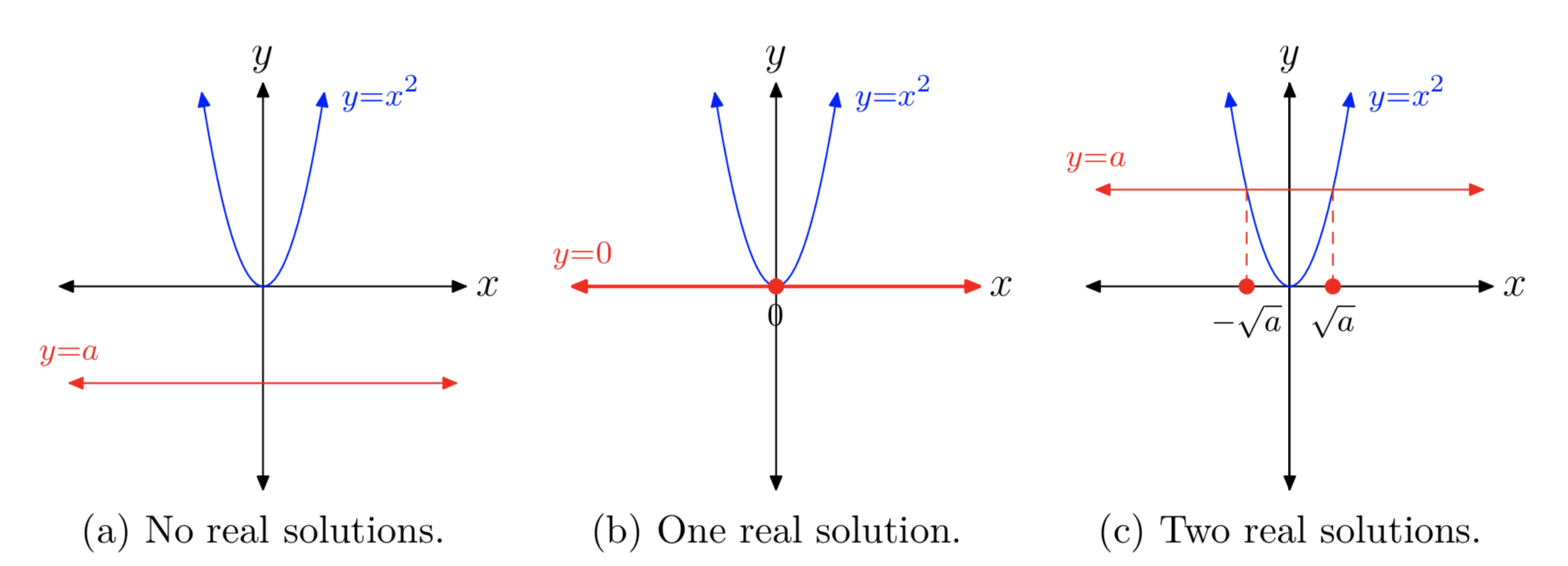
Hay tres casos, cada uno dependiendo del valor y signo de a. en cada caso, la gráfica del lado izquierdo de\(x^2 = a\) es la parábola que se muestra en las Figuras 1 (a), (b) y (c).

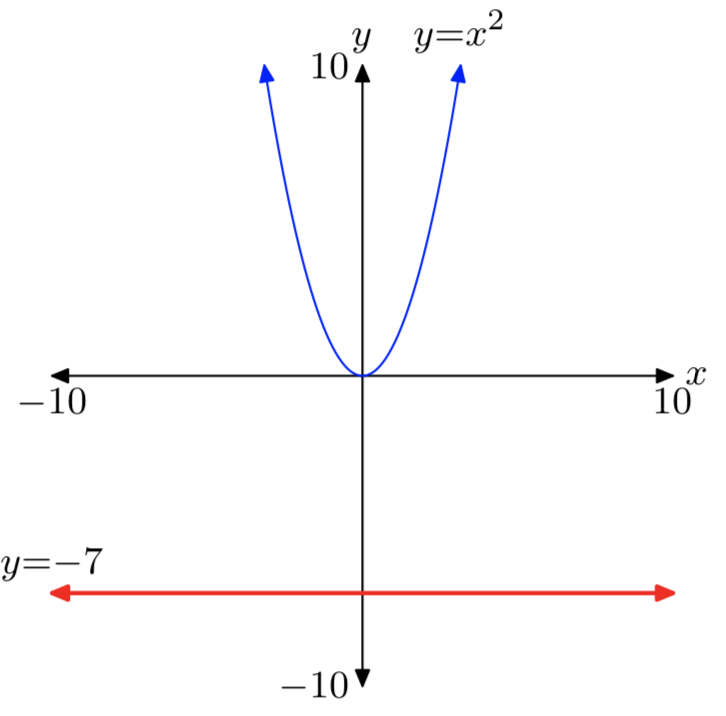
• Caso I: a < 0

  La gráfica del lado derecho de\(x^2 = a\) es una línea horizontal ubicada a unidades por debajo del eje x. De ahí que las gráficas de\(y = x^2\) e y = a no se crucen y la ecuación no\(x^2 = a\) tiene soluciones reales. Este caso se muestra en la Figura 1 (a). De ello se deduce que un número negativo no tiene raíz cuadrada.

• Caso II: a = 0

  La gráfica del lado derecho de\(x^2 = 0\) es una línea horizontal que coincide con el eje x. La gráfica de\(y = x^2\) cruza la gráfica de y = 0 en un punto, en

  el vértice de la parábola. Así, la única solución de\(x^2 = 0\) es x = 0, como se ve en la Figura 2 (b). La solución es la raíz cuadrada de 0, y se denota\(\sqrt{0}\), por lo que sigue\(\sqrt{0} = 0\).

• Caso III: a > 0

  La gráfica del lado derecho de\(x^2 = a\) es una línea horizontal ubicada a unidades por encima del eje x. Las gráficas de\(y = x^2\) e y = a tienen dos puntos de intersección, y por lo tanto la ecuación\(x^2 = a\) tiene dos soluciones reales, como se muestra en la Figura 1 (c). Las soluciones de\(x^2 = a\) son\(x = \pm \sqrt{a}\). Obsérvese que tenemos dos notaciones, una que llama a la solución positiva y una segunda que llama a la solución negativa.

Figura 1: Las soluciones de\(x^2 = a\) dependen del signo y valor de\(a\).

Veamos algunos ejemplos.

Ejemplo\(\PageIndex{8}\)

¿Cuáles son las soluciones\(x^2 = −5\)?

La gráfica del lado izquierdo de\(x^2 = −5\) es la parábola representada en la Figura 1 (a). La gráfica del lado derecho de\(x^2 = −5\) es una línea horizontal ubicada 5 unidades por debajo del eje x. Así, las gráficas no se cruzan y la ecuación no\(x^2 = −5\) tiene soluciones reales.

También puedes razonar de la siguiente manera. Se nos pide que busquemos una solución de\(x^2 = −5\), así que debes encontrar un número cuyo cuadrado sea igual a −5. Sin embargo, cada vez que cuadras un número real, el resultado siempre es no negativo (cero o positivo). No es posible cuadrar un número real y obtener −5.

Tenga en cuenta que esto también significa que no es posible tomar la raíz cuadrada de un número negativo. Es decir, no\(\sqrt{−5}\) es un número real.

Ejemplo\(\PageIndex{9}\)

¿Cuáles son las soluciones\(x^2 = 0\)?

Sólo hay una solución, a saber x = 0. Tenga en cuenta que esto significa que\(\sqrt{0} = 0\).

Ejemplo\(\PageIndex{10}\)

¿Cuáles son las soluciones\(x^2 = 25\)?

La gráfica del lado izquierdo de\(x^2 = 25\) es la parábola representada en la Figura 1 (c). La gráfica del lado derecho de\(x^2 = 25\) es una línea horizontal ubicada a 25 unidades por encima del eje x. Las gráficas se cruzarán en dos puntos, por lo que la ecuación\(x^2 = 25\) tiene dos soluciones reales.

Las soluciones de\(x^2 = 25\) se llaman raíces cuadradas de 25 y están escritas\(x = \pm \sqrt{25}\). En este caso, podemos simplificar aún más y escribir\(x = \pm 5\).

Es sumamente importante observar la simetría en la Figura 1 (c) y señalar que tenemos dos soluciones reales, una negativa y otra positiva. Así, necesitamos dos notaciones, una para la raíz cuadrada positiva de 25 y otra para la raíz cuadrada negativa 25.

Tenga en cuenta que\((5)^2 = 25\), por lo que x = 5 es la solución positiva de\(x^2 = 25\). Para la solución positiva, usamos la notación

\(\sqrt{25} = 5\).

Esto se pronuncia “la raíz cuadrada positiva de 25 es 5”.

Por otro lado, tenga en cuenta que\((−5)^2 = 25\), por lo que x = −5 es la solución negativa de\(x^2 = 25\). Para la solución negativa, usamos la notación

\(−\sqrt{25} = −5\).

Esto se pronuncia “la raíz cuadrada negativa de 25 es −5”.

Esta discusión lleva al siguiente resumen detallado.

RESUMEN: Raíz cuadrada

Las soluciones de\(x^2 = a\) se llaman “raíces cuadradas de a”.

• Caso I: a < 0. La ecuación no\(x^2 = a\) tiene soluciones reales.
• Caso II: a = 0. La ecuación\(x^2 = a\) tiene una solución real, a saber x = 0. Así,\(\sqrt{0} = 0\).
• Caso III: a > 0. La ecuación\(x^2 = a\) tiene dos soluciones reales,\(x = \pm \sqrt{a}\). La notación\(\sqrt{a}\) llama a la raíz cuadrada positiva de a, es decir, la solución positiva de\(x^2 = a\). La notación\(−\sqrt{a}\) pide la raíz cuadrada negativa de a, es decir, la solución negativa de\(x^2 = a\).

Raíces cúbicas: Pasemos a la definición de las raíces cúbicas.

Definición\(\PageIndex{11}\)

Dado un número real a, una “raíz cúbica de a” es un número x tal que\(x^3 = a\).

Por ejemplo, 2 es una raíz cúbica de 8 ya que\(2^3 = 8\). Likewise, −4 es una raíz cúbica de −64 desde entonces\((−4)^3 = −64\). Así, tomar la raíz cúbica es lo “opuesto” del cubo, por lo que la definición de raíz cúbica debe estar estrechamente relacionada con la gráfica de\(y = x^3\), the cubing function. Therefore, we look for solutions of

\(x^3 = a\). (12)

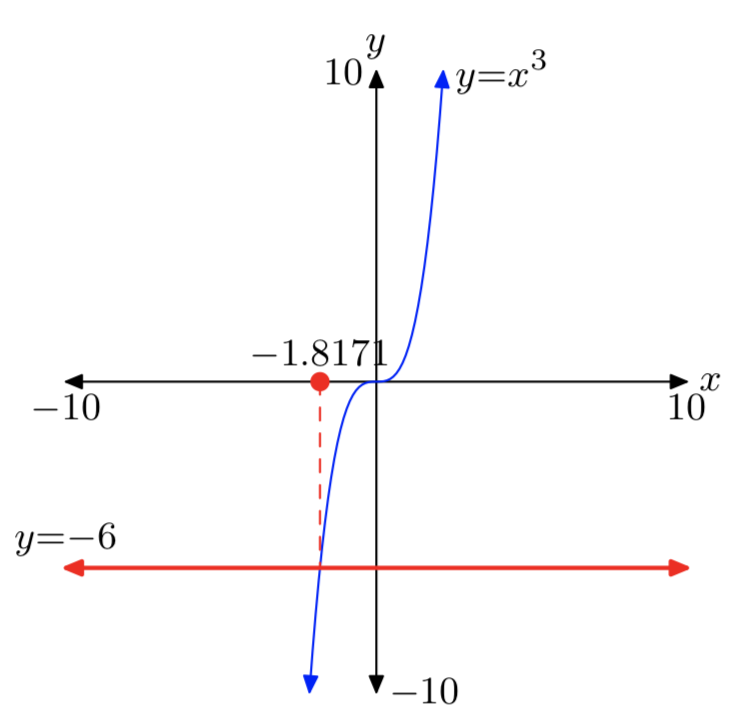
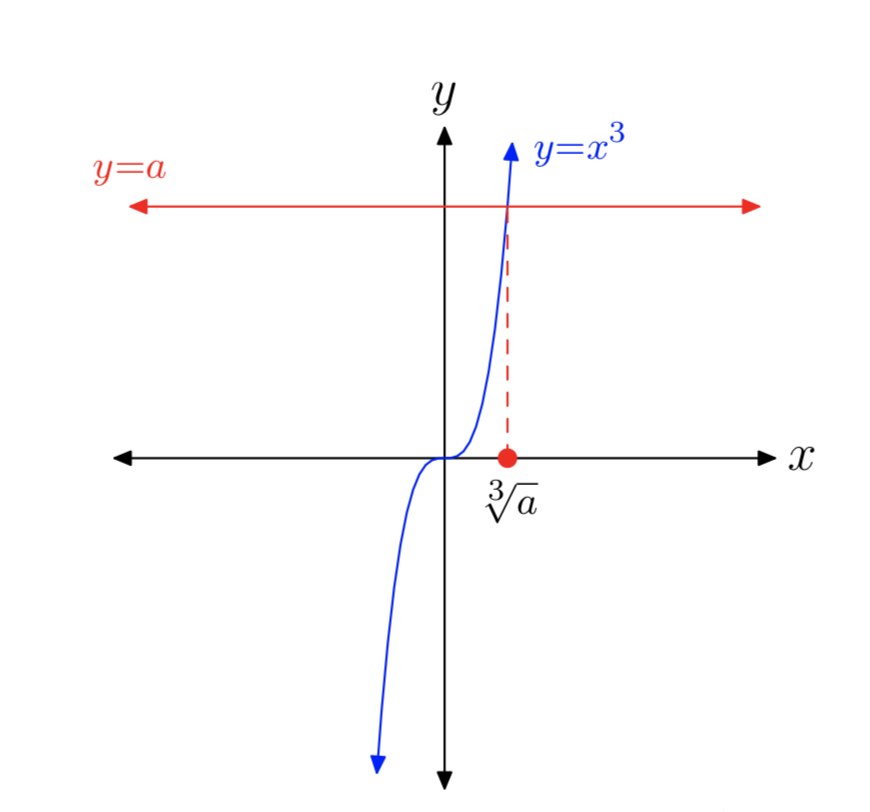
Debido a la forma de la gráfica de\(y = x^3\), sólo hay un caso a considerar. La gráfica del lado izquierdo de\(x^3 = a\) se muestra en la Figura 2. La gráfica del lado derecho de\(x^3 = a\) es una línea horizontal, ubicada una unidad por encima, sobre o por debajo del eje x, dependiendo del signo y valor de a.Independientemente de la ubicación de la línea horizontal y = a, solo habrá un punto de intersección, como se muestra en la Figura 2.

A continuación se presenta un resumen detallado de las raíces cubas.

RESUMEN: Raíz Cubo

Las soluciones de\(x^3 = a\) se llaman las “raíces cubo de a”. Si a es negativo, cero o positivo no hace ninguna diferencia. Hay exactamente una solución real, a saber\(x = \sqrt[3]{a}\).

Figura 2. La gráfica de\(y = x^3\) inter- secc la gráfica de y = a en exactamente un lugar.

Veamos algunos ejemplos.

Ejemplo\(\PageIndex{13}\)

¿Cuáles son las soluciones\(x^3 = 8\)?

La gráfica del lado izquierdo de\(x^3 = 8\) es el polinomio cúbico que se muestra en la Figura 2. La gráfica del lado derecho de\(x^3 = 8\) es una línea horizontal ubicada a 8 unidades por encima del eje x. Las gráficas tienen un punto de intersección, por lo que la ecuación\(x^3 = 8\) tiene exactamente una solución real.

Las soluciones de\(x^3 = 8\) se llaman “raíces cubicas de 8”. Como se muestra en la gráfica, hay exactamente una solución real de\(x^3 = 8\), a saber\(x = \sqrt[3]{8}\). Ahora desde\((2)^3 = 8\), se deduce que x = 2 es una solución real de\(x^3 = 8\). En consecuencia, la raíz cubo de 8 es 2, y escribimos

\(\sqrt[3]{8} = 2\).

Tenga en cuenta que en el caso de la raíz cubo, no hay necesidad de las dos notaciones que vimos en el caso de raíz cuadrada (una para la raíz cuadrada positiva, otra para la raíz cuadrada negativa). Esto se debe a que solo hay una raíz cubo real. Así, la notación\(\sqrt[3]{8}\) se pronuncia “la raíz cubo de 8”.

Ejemplo\(\PageIndex{14}\)

¿Cuáles son las soluciones\(x^3 = 0\)?

Sólo hay una solución de\(x^3 = 0\), namely x = 0. Esto significa que\(\sqrt[3]{0} = 0\).

Ejemplo\(\PageIndex{15}\)

¿Cuáles son las soluciones\(x^3 = −8\)?

La gráfica del lado izquierdo de\(x^3 = −8\) es el polinomio cúbico que se muestra en la Figura 2. La gráfica del lado derecho de\(x^3 = −8\) es una línea horizontal ubicada a 8 unidades por debajo del eje x. Las gráficas tienen solo un punto de intersección, por lo que la ecuación\(x^3 = −8\) tiene exactamente una solución real, denotada\(x = \sqrt[3]{−8}\). Ahora desde\((−2)^3 = −8\), se deduce que x = −2 es una solución real de\(x^3 = −8\). En consecuencia, la raíz cubo de −8 es −2, y escribimos

\(\sqrt[3]{−8} = −2\).

Nuevamente, debido a que solo hay una solución real de\(x^3 = −8\), la notación\(\sqrt[3]{−8}\) se pronuncia “la raíz cúbica de −8”. Tenga en cuenta que, a diferencia de la raíz cuadrada de un número negativo, se permite la raíz cúbica de un número negativo.

Raíces Superiores: Las discusiones anteriores generalizan fácilmente a raíces superiores, como cuartas raíces, quintas raíces, sextas raíces, etc.

Definición\(\PageIndex{16}\)

Dado un número real a y un entero positivo n, una “\(n^{th}\)raíz de a” es un número x tal que\(x^n = a\).

Por ejemplo, 2 es una\(6^{th}\) raíz de 64 ya\(2^6 = 64\) y −3 es una quinta raíz de −243 desde entonces\((−3)^5 = −243\).

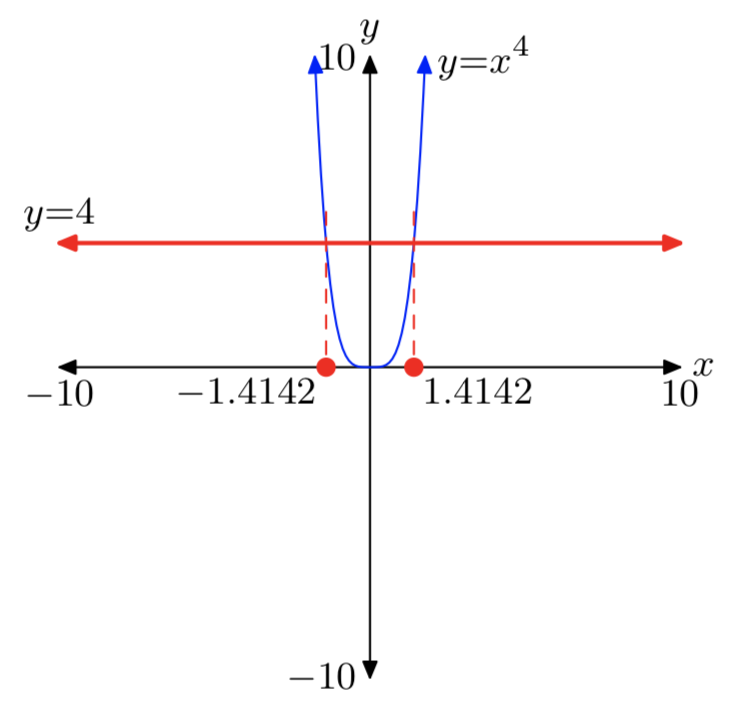
El caso de las raíces pares (es decir, cuando n es par) es muy paralelo al caso de las raíces cuadradas. Eso es porque cuando el exponente n es parejo, la gráfica de se\(y = x^n\) parece mucho a la de\(y = x^2\). Por ejemplo, observe el caso para las cuartas raíces que se muestran en las Figuras 3 (a), (b) y (c).

Figura 3. Las soluciones de\(x^4 = a\) dependen del signo y valor de a.

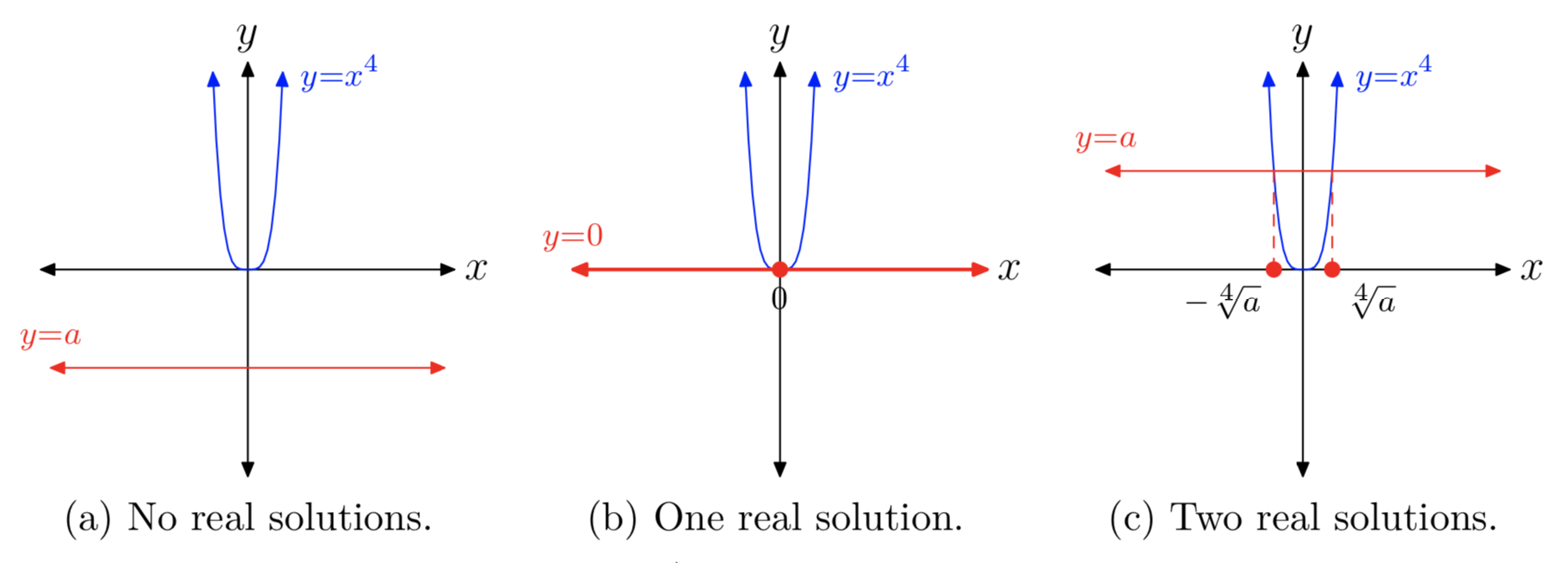
La discusión por\(n^{th}\) raíces pares es muy paralela a la presentada en la introducción de raíces cuadradas, por lo que sin más preámbulos, vamos directamente al resumen.

RESUMEN: INCLUSO\(N^{th}\) ROOT

Si n es un entero par positivo, entonces las soluciones de\(x^n = a\) se llaman “\(n^{th}\)raíces de a”.

• Caso I: a < 0. La ecuación no\(x^n = a\) tiene soluciones reales.
• Caso II: a = 0. La ecuación\(x^n = a\) tiene exactamente una solución real, a saber x = 0. Así,\(\sqrt[n]{0} = 0\).
• Caso III: a > 0. La ecuación\(x^n =a\) tiene dos soluciones reales,\(x = \pm \sqrt[n]{a}\). La notación\(\sqrt[n]{a}\) llama a la\(n^{th}\) raíz positiva de una, es decir, la solución positiva de\(x^n = a\). La notación\(−\sqrt[n]{a}\) pide la\(n^{th}\) raíz negativa de a, es decir, la solución negativa de\(x^n = a\).

Asimismo, el caso de las raíces impares (es decir, cuando n es impar) es muy paralelo al caso de las raíces cúbicas. Eso es porque cuando el exponente n es impar, la gráfica de se\(y = x^n\) parece mucho a la de\(y = x^3\). Por ejemplo, observe el caso de quintas raíces que se muestra en la Figura 4.

Figura 4. La gráfica de\(y = x^5\) cruza la gráfica de y = a en exactamente un lugar.

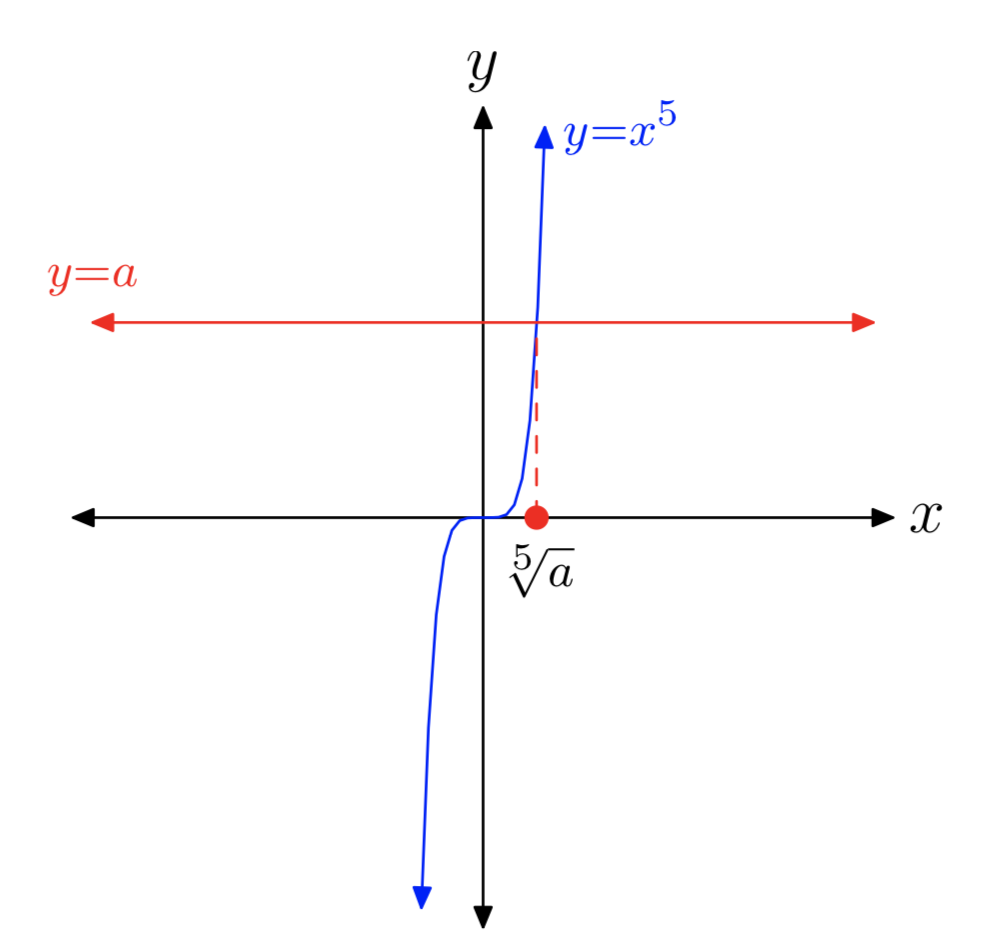
La discusión de\(n^{th}\) raíces extrañas es muy paralela a la introducción de las raíces cúbicas que discutimos anteriormente. Entonces, sin más preámbulos, procedemos directamente al resumen.

RESUMEN: ODD\(N^{th}\) ROOT

Si n es un entero impar positivo, entonces las soluciones de\(x^n = a\) se llaman las “\(n^{th}\)raíces de a”. Si a es negativo, cero o positivo no hace ninguna diferencia. Hay exactamente una solución real de\(x^n = a\), denotada\(x = \sqrt[n]{a}\).

OBLACIÓN 17. Los símbolos\(\sqrt{}\) y\(\sqrt[n]{}\) para la raíz cuadrada y\(n^{th}\) root, respectively, are also called radicals.

Cerraremos esta sección con algunos ejemplos más.

Ejemplo\(\PageIndex{18}\)

¿Cuáles son las soluciones\(x^4 = 16\)?

La gráfica del lado izquierdo de\(x^4 = 16\) es el polinomio cuártico que se muestra en la Figura 3 (c). La gráfica del lado derecho de\(x^4 = 16\) es una línea horizontal, ubicada 16 unidades por encima del eje x. Las gráficas se cruzarán en dos puntos, por lo que la ecuación\(x^4 = 16\) tiene dos soluciones reales.

Las soluciones de\(x^4 = 16\) se llaman cuartas raíces de 16 y están escritas\(x = \pm \sqrt[4]{16}\). Es sumamente importante señalar la simetría en la Figura 3 (c) y señalar que tenemos dos soluciones reales de\(x^4 = 16\), una de las cuales es negativa y la otra positiva. De ahí que necesitamos dos notaciones, una para la cuarta raíz positiva de 16 y otra para la cuarta raíz negativa de 16.

Tenga en cuenta que\(2^4 = 16\), por lo que x = 2 es la solución real positiva de\(x^4 = 16\). Para esta solución positiva, utilizamos la notación

\(\sqrt[4]{16} = 2\).

Esto se pronuncia “la cuarta raíz positiva de 16 es 2”.

Por otro lado, tenga en cuenta que\((−2)^4 = 16\), por lo que x = −2 es la solución real negativa de\(x^4 = 16\). Para esta solución negativa, usamos la notación

\(−\sqrt[4]{16} = −2\). (19)

Esto se pronuncia “la cuarta raíz negativa de 16 es −2”.

Ejemplo\(\PageIndex{19}\)

¿Cuáles son las soluciones\(x^5 = −32\)?

La gráfica del lado izquierdo de\(x^5 = −32\) es el polinomio quintico representado en la Figura 4. La gráfica del lado derecho de\(x^5 = −32\) es una línea horizontal, ubicada 32 unidades por debajo del eje x. Las gráficas tienen un punto de intersección, por lo que la ecuación\(x^5 = −32\) tiene exactamente una solución real.

Las soluciones de\(x^5 = −32\) se llaman “quintas raíces de −32”. Como se muestra en la gráfica, hay exactamente una solución real de\(x^5 = −32\), a saber\(x = \sqrt[5]{−32}\). Ahora desde\((−2)^5 = −32\), se deduce que x = −2 es una solución de\(x^5 = −32\). En consecuencia, la quinta raíz de −32 es −2, y escribimos

\(\sqrt[5]{−32} = −2\).

Debido a que solo hay una solución real, la notación\(\sqrt[5]{−32}\) se pronuncia “la quinta raíz de −32”. Nuevamente, a diferencia de la raíz cuadrada o cuarta raíz de un número negativo, se permite la quinta raíz de un número negativo.

No todas las raíces simplifican a números racionales. Si ese fuera el caso, ni siquiera sería necesario implementar la notación radical. Considera el siguiente ejemplo.

EXAMPL\(\PageIndex{20}\)

Encuentra todas las soluciones reales de la ecuación\(x^2 = 7\), tanto gráfica como algebraicamente, y compara tus resultados.

Fácilmente podríamos esbozar gráficos aproximados de\(y = x^2\) e y = 7 a mano, pero busquemos un mayor nivel de precisión pidiendo a la calculadora gráfica que se encargue de esta tarea.

• Cargue la ecuación\(y = x^2\) e y = 7 en Y1 e Y2 en el menú Y= de la calculadora, respectivamente. Esto se muestra en la Figura 5 (a).
• Utilice la utilidad de intersección en la calculadora gráfica para encontrar las coordenadas de los puntos de intersección. Las coordenadas x de estos puntos, mostradas en la Figura 5 (b) y (c), son las soluciones a la ecuación\(x^2 = 7\).

Figura 5. Las soluciones de\(x^2 = 7\) son\(x \approx −2.645751\) o\(x \approx 2.6457513\).

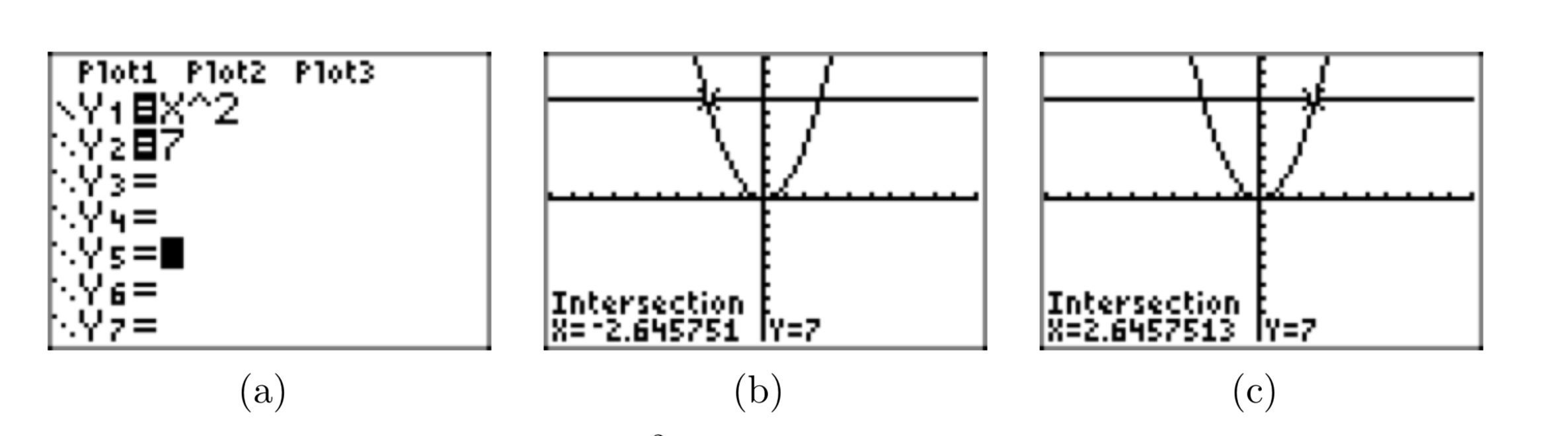
Lineamientos para Soluciones de Calculadora Gráfica de Informes. Recuerde el método estándar para reportar los resultados de la calculadora gráfica en su tarea:

• Copia la imagen de tu ventana de visualización en tu papel de tarea. Marcar y escalar cada eje con xmin, xmax, ymin e ymax, luego etiquetar cada gráfica con su ecuación, como se muestra en la Figura 6.
• Suelte líneas verticales discontinuas desde cada punto de intersección hasta el eje x. Sombra y etiquete sus soluciones en el eje x.

Figura 6. Las soluciones de\(x^2 = 7\) son\(x \approx −2.645751\) o\(x \approx 2.6457513\).

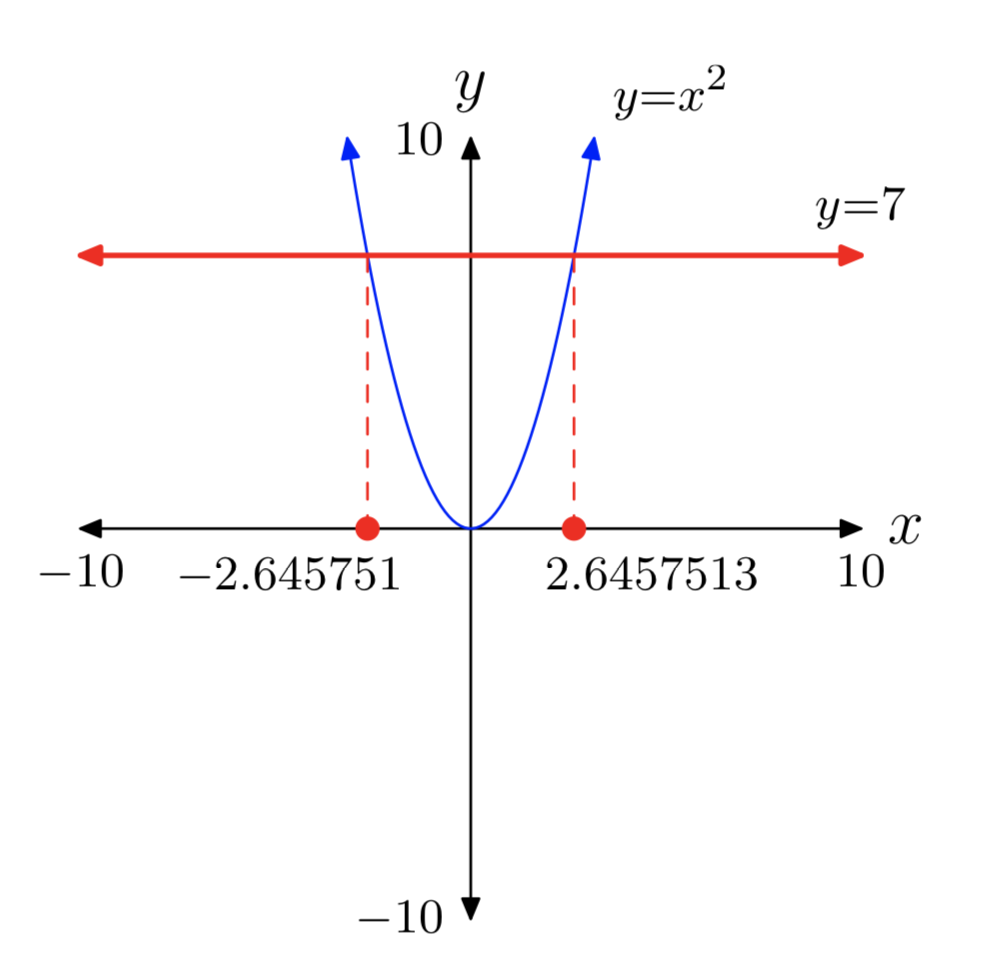
De ahí que las soluciones aproximadas sean\(x \approx −2.645751\) o\(x \approx 2.6457513\).

Por otro lado, para encontrar soluciones analíticas de\(x^2 = 7\), simplemente tomamos más o menos la raíz cuadrada de 7.

\(x^2 = 7\)

\(\sqrt{x} = \pm 7\)

Para comparar estas soluciones exactas con las soluciones aproximadas encontradas mediante el uso de la calculadora gráfica, utilice una calculadora para calcular\(\pm \sqrt{7}\), como se muestra en la Figura 7.

Figura 7. Aproximando\(\pm \sqrt{7}\).

Tenga en cuenta que estas aproximaciones\(−\sqrt{7}\) y\(\sqrt{7}\) concuerdan bastante bien con las soluciones encontradas usando la utilidad de intersección de la calculadora gráfica y reportadas en la Figura 6.

Ambos\(−\sqrt{7}\) y\(\sqrt{7}\) son ejemplos de números irracionales, es decir, números que no se pueden expresar en la forma\(\frac{p}{q}\), donde p y q son números enteros.

Exponentes racionales

Al igual que con la definición de exponentes negativos y cero, discutida anteriormente en esta sección, resulta que los exponentes racionales pueden definirse de tal manera que las Leyes de los Exponentes seguirán aplicándose (y de hecho, solo hay una manera de hacerlo).

La tercera ley nos da una pista sobre cómo definir exponentes racionales. Por ejemplo, supongamos que queremos definir\(2^{\frac{1}{3}}\). Entonces por la tercera ley,

\((2^{\frac{1}{3}})^3 = 2^{\frac{1}{3} \cdot 3} = 2^1 = 2\),

entonces, tomando raíces cúbicas de ambos lados, debemos\(2^{\frac{1}{3}}\) definir. por la fórmula

\(2^{\frac{1}{3}} = \sqrt[3]{2}\).

El mismo argumento muestra que si n es cualquier entero positivo impar, entonces\(2^{\frac{1}{n}}\) debe definirse por la fórmula

\(2^{\frac{1}{n}} = \sqrt[n]{2}\).

Sin embargo, para un número entero par n, parece haber una opción. Supongamos que queremos definir\(2^{\frac{1}{2}}\). Entonces

\((2^{\frac{1}{2}})^2 = 2^{\frac{1}{2} \cdot 2} = 2^1 = 2\),

entonces,

\(2^{\frac{1}{2}} = \sqrt{2}\).

Sin embargo, la elección negativa para el exponente\(\frac{1}{2}\) genera problemas, porque entonces no se definen ciertas expresiones. Por ejemplo, de la tercera ley se desprendería que

\((2^{\frac{1}{2}})^\frac{1}{2} = −\sqrt{−\sqrt{2}}\).

Pero\(−\sqrt{2}\) es negativo, entonces no\(\sqrt{−\sqrt{2}}\) está definido. Por lo tanto, sólo tiene sentido utilizar la opción positiva. Así, para todo n, par e impar,\(2^{\frac{1}{n}}\) se define por la fórmula

\(2^{\frac{1}{n}} = \sqrt[n]{2}\).

De manera similar, para una racional positiva general\(\frac{m}{n}\) la tercera ley implica que

\(2^{\frac{m}{n}} = (2^m)^{\frac{1}{n}} = \sqrt[n]{2^m}\)

Pero también,

\(2^{\frac{m}{n}} = (2^{\frac{1}{n}})^m = (\sqrt[n]{2})^m\)

Por lo tanto,

\(2^{\frac{m}{n}} = \sqrt[n]{2^m} = (\sqrt[n]{2})^m\)

Finalmente, los exponentes racionales negativos se definen de la manera habitual para los exponentes negativos:

\(2^{−\frac{m}{n}} = \frac{1}{2^{\frac{m}{n}}}\)

De manera más general, aquí está la definición general final. Con esta definición, las Leyes de los Exponentes sostienen para todos los exponentes racionales.

Definición\(\PageIndex{22}\)

Para un exponente racional positivo\(\frac{m}{n}\), y b > 0

\(b^{\frac{m}{n}} = \sqrt[n]{b^m} = (\sqrt[n]{b})^m\)(23)

Para un exponente racional negativo\(−\frac{m}{n}\),

\(b^{−\frac{m}{n}} = \frac{1}{b^{\frac{m}{n}}}\)(24)

OBSERVACIÓN 25. Para b < 0, las mismas definiciones tienen sentido solo cuando n es impar. Por ejemplo no\((−2)^{\frac{1}{4}}\) está definido.

Ejemplo\(\PageIndex{26}\)

Compute los valores exactos de

(a)\(4^{\frac{5}{2}}\)

b)\(64^{\frac{2}{3}}\)

c)\(81^{−\frac{3}{4}}\)

Contestar

(a)\(4^{\frac{5}{2}} = (4^{\frac{1}{2}})^5 = (\sqrt{4})^5 = 2^5 = 32\)

b)\(64^{\frac{2}{3}} = (64^\frac{1}{3})^2 = (\sqrt[3]{64})^2 = 4^2 = 16\)

c)\(81^{−\frac{3}{4}} = \frac{1}{81^{\frac{3}{4}}} = \frac{1}{(81^{\frac{1}{4}})^3} = \frac{1}{3^3} = \frac{1}{27}\)

Ejemplo\(\PageIndex{27}\)

Simplifica las siguientes expresiones y escríbelas en la forma\(x^r\):

(a)\(x^{\frac{2}{3}}x^{\frac{1}{4}}\)

b)\(\frac{x^{\frac{2}{3}}}{x^{\frac{1}{4}}}\)

c)\((x^{−\frac{2}{3}})^{\frac{1}{4}}\)

Contestar

(a)\(x^{\frac{2}{3}}x^{\frac{1}{4}} = x^{\frac{2}{3}+\frac{1}{4}} = x^{\frac{11}{12}}\)

b)\(\frac{x^{\frac{2}{3}}}{x^{\frac{1}{4}}} = x^{\frac{2}{3}−\frac{1}{4}} = x^{\frac{5}{12}}\)

c)\((x^{−\frac{2}{3}})^{\frac{1}{4}} = x^{−\frac{2}{3} \cdot \frac{1}{4}} = x^{−\frac{1}{6}}\)

Ejemplo\(\PageIndex{28}\)

Usa exponentes racionales para simplificar\(\sqrt[5]{\sqrt{x}}\), y escríbalo como un solo radical.

Contestar

\(\sqrt[5]{\sqrt{x}} = (\sqrt{x})^{\frac{1}{5}} = (x^{\frac{1}{2}})^{\frac{1}{5}} = (x^{\frac{1}{2} \cdot \frac{1}{5}} = x^{\frac{1}{10}} = \sqrt[10]{x}\)

Ejemplo\(\PageIndex{29}\)

Use una calculadora para aproximar\(2^{\frac{5}{8}}\).

Contestar

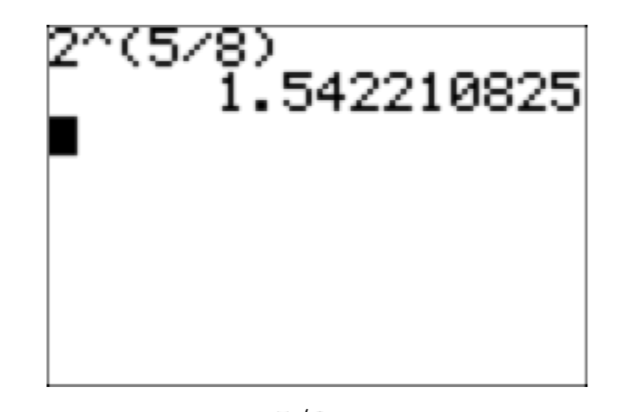
Figura 8. \(2^{\frac{5}{8}} \approx 1.542210825\)

Exponentes irracionales

¿Qué pasa con los exponentes irracionales? ¿Hay alguna manera de definir números como\(2^{\sqrt{2}}\) y\(3^{\pi}\)? Resulta que la respuesta es sí. Si bien una definición rigurosa de\(b^s\) cuándo s es irracional está más allá del alcance de este libro, no es difícil ver cómo se podría proceder a encontrar un valor para tal número. Por ejemplo, si queremos calcular el valor de\(2^{\sqrt{2}}\), podemos comenzar con aproximaciones racionales para\(\sqrt{2}\). Desde\(\sqrt{2}\) = 1.41421356237310.., los poderes sucesivos

\(2^1\),\(2^{1.4}\),\(2^{1.41}\)\(2^{1.414}\),\(2^{1.4142}\),\(2^{1.41421}\),\(2^{1.414213}\),\(2^{1.4142135}\),\(2^{1.41421356}\),\(2^{1.414213562}\)\(2^{1.4142135623}\),,,.

deben ser aproximaciones cada vez más cercanas al valor deseado de\(2^{\sqrt{2}}\).

De hecho, utilizando una teoría matemática más avanzada (basada en última instancia en la construcción real del sistema de números reales), se puede demostrar que estas potencias se acercan\(2^{\sqrt{2}}\) a un solo número real, y definimos que es ese número. Usando su calculadora, puede observar esta convergencia y obtener una aproximación calculando las potencias anteriores.

Figura 9.

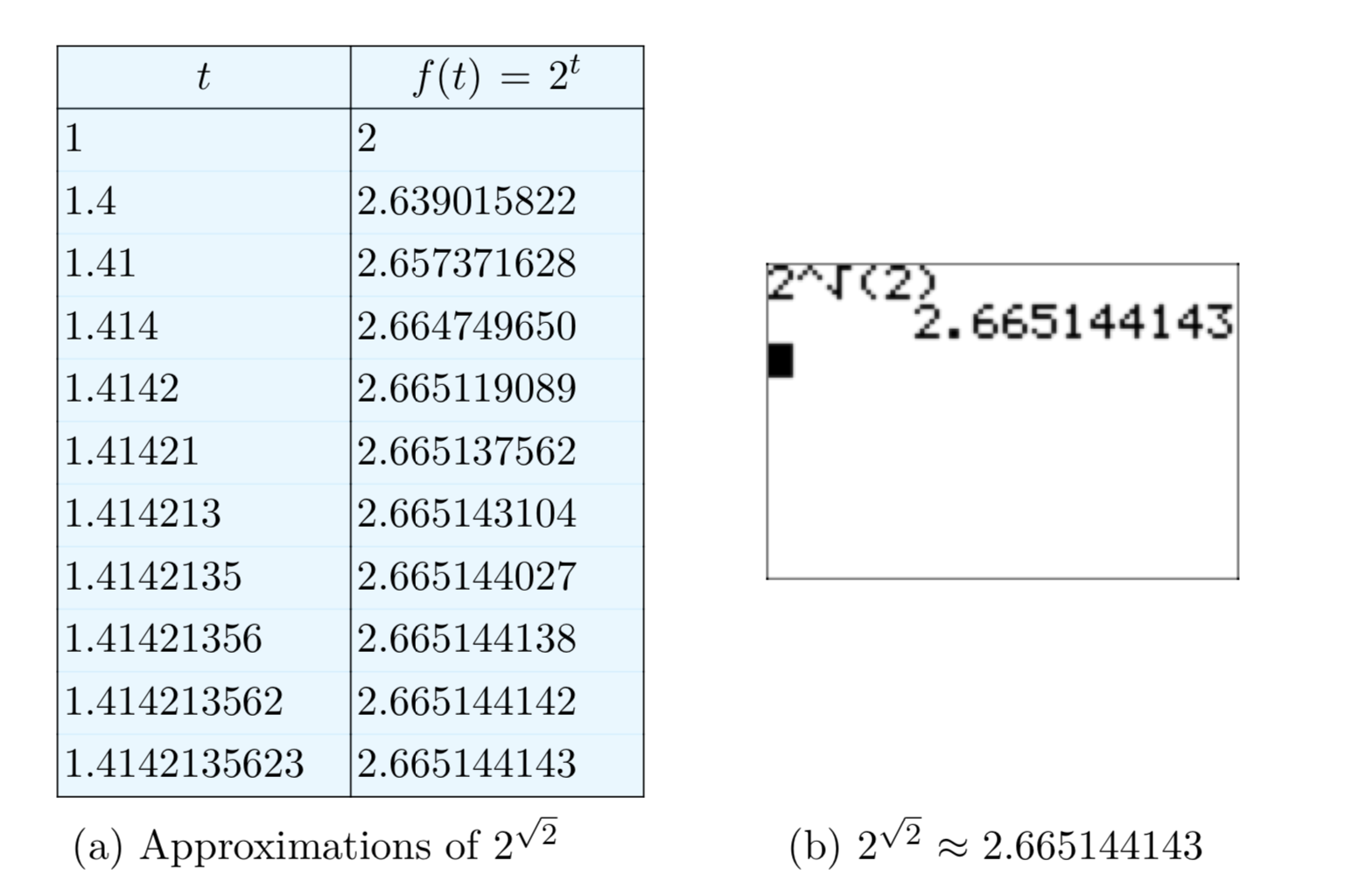
El último valor de la tabla de la Figura 9 (\(2^{\sqrt{2}}\)a) es una aproximación correcta de 10 dígitos de precisión. Su calculadora obtendrá esta misma aproximación cuando le pidan que compute\(2^{\sqrt{2}}\) directamente (ver Figura 9 (b)).

De manera similar, se\(b^s\) puede definir para cualquier exponente irracional s y cualquier b > 0. Combinado con el trabajo anterior en esta sección, se deduce que\(b^s\) se define para cada exponente real s.

Ejercicio

En los Ejercicios 1 - 12, computa el valor exacto.

Ejercicio\(\PageIndex{1}\)

\(3^{−5}\)

Contestar

\(\frac{1}{243}\)

Ejercicio\(\PageIndex{2}\)

\(4^2\)

Ejercicio\(\PageIndex{3}\)

\((\frac{3}{2})^3\)

Contestar

\(\frac{27}{8}\)

Ejercicio\(\PageIndex{4}\)

\((\frac{2}{3})^1\)

Ejercicio\(\PageIndex{5}\)

\(6^{−2}\)

Contestar

\(\frac{1}{36}\)

Ejercicio\(\PageIndex{6}\)

\(4^{−3}\)

Ejercicio\(\PageIndex{7}\)

\((\frac{2}{3})^{−3}\)

Contestar

\(\frac{27}{8}\)

Ejercicio\(\PageIndex{8}\)

\((\frac{1}{3})^{−3}\)

Ejercicio\(\PageIndex{9}\)

\(7^1\)

Contestar

7

Ejercicio\(\PageIndex{10}\)

\((\frac{3}{2})^{−4}\)

Ejercicio\(\PageIndex{11}\)

\((\frac{5}{6})^3\)

Contestar

\(\frac{125}{216}\)

Ejercicio\(\PageIndex{12}\)

\(3^2\)

En los Ejercicios 13 - 24, realice cada una de las siguientes tareas para la ecuación dada.

1. Cargue los lados izquierdo y derecho de la ecuación dada en Y1 e Y2, respectivamente. Ajuste los parámetros de VENTANA hasta que todos los puntos de intersección (si los hubiera) estén visibles en su ventana de visualización. Utilice la utilidad Intersecar en el menú CALC para determinar las coordenadas de cualquier punto de intersección.
2. Haga una copia de la imagen en su ventana de visualización en su papel de tarea. Etiquetar y escalar cada eje con xmin, xmax, ymin e ymax. Etiquete cada gráfica con su ecuación. Coloque líneas verticales discontinuas desde cada punto de intersección hasta el eje x, luego sombree y etiquete cada solución de la ecuación dada en el eje x. Recuerda dibujar todas las líneas con una regla.
3. Resolver cada problema algebraicamente. Use una calculadora para aproximar cualquier radical y compare estas soluciones con las que se encuentran en las partes (1) y (2).

Ejercicio\(\PageIndex{13}\)

\(x^2 = 5\)

Contestar

\(x = \pm \sqrt{5}\)

Ejercicio\(\PageIndex{14}\)

\(x^2 = 7\)

Ejercicio\(\PageIndex{15}\)

\(x^2 = −7\)

Contestar

No hay soluciones reales.

Ejercicio\(\PageIndex{16}\)

\(x^2 = −3\)

Ejercicio\(\PageIndex{17}\)

\(x^3 = −6\)

Contestar

\(x = \sqrt[3]{−6}\)

Ejercicio\(\PageIndex{18}\)

\(x^3 = −4\)

Ejercicio\(\PageIndex{19}\)

\(x^4 = 4\)

Contestar

\(x = \pm \sqrt[4]{4}\)

Ejercicio\(\PageIndex{20}\)

\(x^4 = −7\)

Ejercicio\(\PageIndex{21}\)

\(x^5 = 8\)

Contestar

\(x = \sqrt[5]{8}\)

Ejercicio\(\PageIndex{22}\)

\(x^5 = 4\)

Ejercicio\(\PageIndex{23}\)

\(x^6 = −5\)

Contestar

No hay soluciones reales.

Ejercicio\(\PageIndex{24}\)

\(x^6 = 9\)

En los Ejercicios 25 - 40, simplificar la expresión radical dada.

Ejercicio\(\PageIndex{25}\)

\(\sqrt{49}\)

Contestar

7

Ejercicio\(\PageIndex{26}\)

\(\sqrt{121}\)

Ejercicio\(\PageIndex{27}\)

\(\sqrt{−36}\)

Contestar

No es un número real.

Ejercicio\(\PageIndex{28}\)

\(\sqrt{−100}\)

Ejercicio\(\PageIndex{29}\)

\(\sqrt[3]{−1}\)

Contestar

3

Ejercicio\(\PageIndex{30}\)

\(\sqrt[3]{−1}\)

Ejercicio\(\PageIndex{31}\)

\(\sqrt[3]{−125}\)

Contestar

−5

Ejercicio\(\PageIndex{32}\)

\(\sqrt[3]{64}\)

Ejercicio\(\PageIndex{33}\)

\(\sqrt[4]{−16}\)

Contestar

No es un número real.

Ejercicio\(\PageIndex{34}\)

\(\sqrt[4]{81}\)

Ejercicio\(\PageIndex{35}\)

\(\sqrt[4]{16}\)

Contestar

2

Ejercicio\(\PageIndex{36}\)

\(\sqrt[3]{−625}\)

Ejercicio\(\PageIndex{37}\)

\(\sqrt[5]{−32}\)

Contestar

−2

Ejercicio\(\PageIndex{38}\)

\(\sqrt[5]{243}\)

Ejercicio\(\PageIndex{39}\)

\(\sqrt[5]{1024}\)

Contestar

4

Ejercicio\(\PageIndex{40}\)

\(\sqrt[5]{−3125}\)

Ejercicio\(\PageIndex{41}\)

Comparar y contrastar\(\sqrt{(−2)^2}\) y\((\sqrt{−2})^2\).

Contestar

\(\sqrt{(−2)^2} = 2\), mientras que no\((\sqrt{−2})^2\) es un número real.

Ejercicio\(\PageIndex{42}\)

Comparar y contrastar\(\sqrt[4]{(−3)^4}\) y\((\sqrt[4]{−3})^4\).

Ejercicio\(\PageIndex{43}\)

Comparar y contrastar\(\sqrt[3]{(−5)^3}\) y\((\sqrt[3]{−5})^3\).

Contestar

Ambos son iguales −5.

Ejercicio\(\PageIndex{44}\)

Comparar y contrastar\(\sqrt[5]{(−2)^5}\) y\((\sqrt[5]{−2})^5\).

En los Ejercicios 45 - 56, computa el valor exacto.

Ejercicio\(\PageIndex{45}\)

\(25^{−\frac{3}{2}}\)

Contestar

\(\frac{1}{125}\)

Ejercicio\(\PageIndex{46}\)

\(16^{−\frac{5}{4}}\)

Ejercicio\(\PageIndex{47}\)

\(8^{\frac{4}{3}}\)

Contestar

16

Ejercicio\(\PageIndex{48}\)

\(625^{−\frac{3}{4}}\)

Ejercicio\(\PageIndex{49}\)

\(16^{\frac{3}{2}}\)

Contestar

64

Ejercicio\(\PageIndex{50}\)

\(64^{\frac{2}{3}}\)

Ejercicio\(\PageIndex{51}\)

\(27^{\frac{2}{3}}\)

Contestar

9

Ejercicio\(\PageIndex{52}\)

\(625^{\frac{3}{4}}\)

Ejercicio\(\PageIndex{53}\)

\(256^{\frac{5}{4}}\)

Contestar

1024

Ejercicio\(\PageIndex{54}\)

\(4^{−\frac{3}{2}}\)

Ejercicio\(\PageIndex{55}\)

\(256^{−\frac{3}{4}}\)

Contestar

\(\frac{1}{64}\)

Ejercicio\(\PageIndex{56}\)

\(81^{−\frac{5}{4}}\)

En Ejercicios 57 - 64, simplifica el producto, y escribe tu respuesta en el formulario\(x^r\).

Ejercicio\(\PageIndex{57}\)

\(x^{\frac{5}{4}}x^{\frac{5}{4}}\)

Contestar

\(x^{\frac{5}{2}}\)

Ejercicio\(\PageIndex{58}\)

\(x^{\frac{5}{3}}x^{−\frac{5}{4}}\)

Ejercicio\(\PageIndex{59}\)

\(x^{−\frac{1}{3}}x^{\frac{5}{2}}\)

Contestar

\(x^{\frac{13}{6}}\)

Ejercicio\(\PageIndex{60}\)

\(x^{−\frac{3}{5}}x^{\frac{3}{2}}\)

Ejercicio\(\PageIndex{61}\)

\(x^{\frac{4}{5}}x^{−\frac{4}{3}}\)

Contestar

\(x^{−\frac{8}{15}}\)

Ejercicio\(\PageIndex{62}\)

\(x^{−\frac{5}{4}}x^{\frac{1}{2}}\)

Ejercicio\(\PageIndex{63}\)

\(x^{−\frac{2}{5}}x^{−\frac{3}{2}}\)

Responder

\(x^{−\frac{19}{10}}\)

Ejercicio\(\PageIndex{64}\)

\(x^{−\frac{5}{4}}x^{\frac{5}{2}}\)

En los Ejercicios 65 - 72, simplifica el cociente, y escribe tu respuesta en la forma\(x^r\).

Ejercicio\(\PageIndex{65}\)

\(\frac{x^{−\frac{5}{4}}}{x^{\frac{1}{5}}}\)

Responder

\(x^{−\frac{29}{20}}\)

Ejercicio\(\PageIndex{66}\)

\(\frac{x^{−\frac{2}{3}}}{x^{\frac{1}{4}}}\)

Ejercicio\(\PageIndex{67}\)

\(\frac{x^{−\frac{1}{2}}}{x^{−\frac{3}{5}}}\)

Responder

\(x^{\frac{1}{10}}\)

Ejercicio\(\PageIndex{68}\)

\(\frac{x^{−\frac{5}{2}}}{x^{\frac{5}{2}}}\)

Ejercicio\(\PageIndex{69}\)

\(\frac{x^{\frac{3}{5}}}{x^{−\frac{1}{4}}}\)

Responder

\(x^{\frac{17}{20}}\)

Ejercicio\(\PageIndex{70}\)

\(\frac{x^{\frac{1}{3}}}{x^{−\frac{1}{2}}}\)

Ejercicio\(\PageIndex{71}\)

\(\frac{x^{−\frac{5}{4}}}{x^{\frac{2}{3}}}\)

Responder

\(x^{−\frac{23}{12}}\)

Ejercicio\(\PageIndex{72}\)

\(\frac{x^{\frac{1}{3}}}{x^{\frac{1}{2}}}\)

En Ejercicios 73 - 80, simplifica la expresión, y escribe tu respuesta en la forma\(x^r\).

Ejercicio\(\PageIndex{73}\)

\((x^{\frac{1}{2}})^{\frac{4}{3}}\)

Responder

\(x^{\frac{2}{3}}\)

Ejercicio\(\PageIndex{74}\)

\((x^{−\frac{1}{2}})^{−\frac{1}{2}}\)

Ejercicio\(\PageIndex{75}\)

\((x^{−\frac{5}{4}})^{\frac{1}{2}}\)

Responder

\(x^{−\frac{5}{8}}\)

Ejercicio\(\PageIndex{76}\)

\((x^{−\frac{1}{5}})^{−\frac{3}{2}}\)

Ejercicio\(\PageIndex{77}\)

\((x^{−\frac{1}{2}})^{\frac{3}{2}}\)

Responder

\(x^{−\frac{3}{4}}\)

Ejercicio\(\PageIndex{78}\)

\((x^{−\frac{1}{3}})^{−\frac{1}{2}}\)

Ejercicio\(\PageIndex{79}\)

\((x^{\frac{1}{5}})^{−\frac{1}{2}}\)

Responder

\(x^{−\frac{1}{10}}\)

Ejercicio\(\PageIndex{80}\)

\((x^{\frac{2}{5}})^{−\frac{1}{5}}\)

​​​​​​​