9.1: La función de raíz cuadrada

Última actualización
Guardar como PDF

Page ID: 110691

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En esta sección volvemos nuestra atención a la función raíz cuadrada, la función definida por la ecuación

\[\begin{array}{c} {f(x)= \sqrt{x}}\\ \end{array}\]

Comenzamos la sección dibujando la gráfica de la función, luego abordamos el dominio y el rango. Después de eso, investigaremos una serie de transformaciones diferentes de la función.

La Gráfica de la Función de Raíz Cuadrada

Vamos a crear una tabla de puntos que satisfagan la ecuación de la función, luego trazar los puntos de la tabla en un sistema de coordenadas cartesianas en papel cuadriculado. Seguiremos creando y trazando puntos hasta que estemos convencidos de la eventual forma de la gráfica.

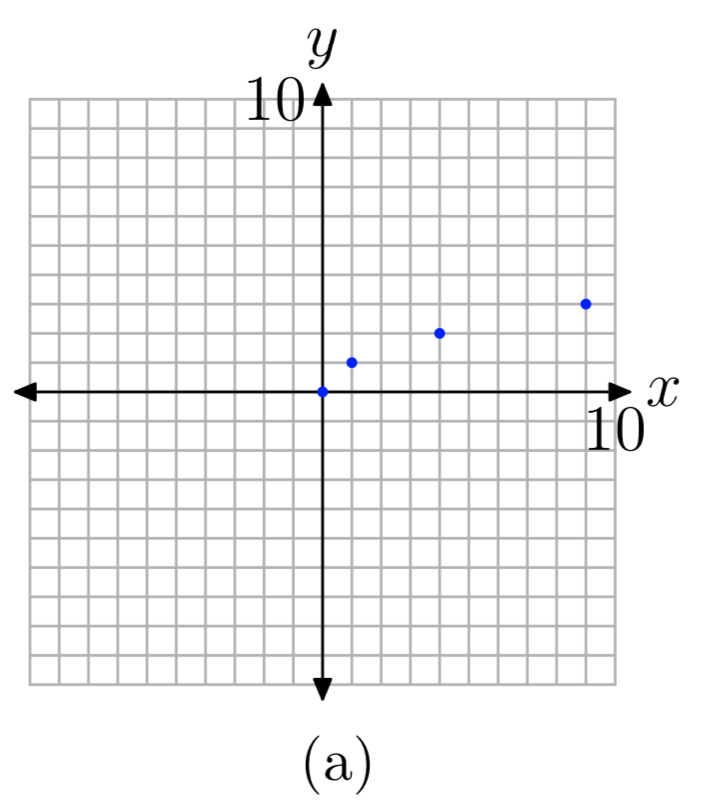
Sabemos que no podemos tomar la raíz cuadrada de un número negativo. Por lo tanto, no queremos poner ningún valor x negativo en nuestra tabla. Para simplificar aún más nuestros cálculos, usemos números cuya raíz cuadrada se calcula fácilmente. Esto trae a la mente cuadrados perfectos como 0, 1, 4, 9, y así sucesivamente. Hemos colocado estos números como valores x en la tabla de la Figura 1 (b), luego calculamos la raíz cuadrada de cada uno. En la Figura 1 (a), se ve cada uno de los puntos de la tabla trazados como un punto sólido. Si seguimos sumando puntos a la tabla, los trazamos, la gráfica eventualmente se rellenará y tomará la forma de la curva sólida que se muestra en la Figura 1 (c).

Screen Shot 2019-05-24 a las 3.15.38 PM.png — Figura 1.} \ text {Creando la gráfica de} f (x) =\ sqrt {x}}\\\ nonumber\ end {array}\]

Screen Shot 2019-05-24 a las 3.15.46 PM.png — Figura 1.} \ text {Creando la gráfica de} f (x) =\ sqrt {x}}\\\ nonumber\ end {array}\]

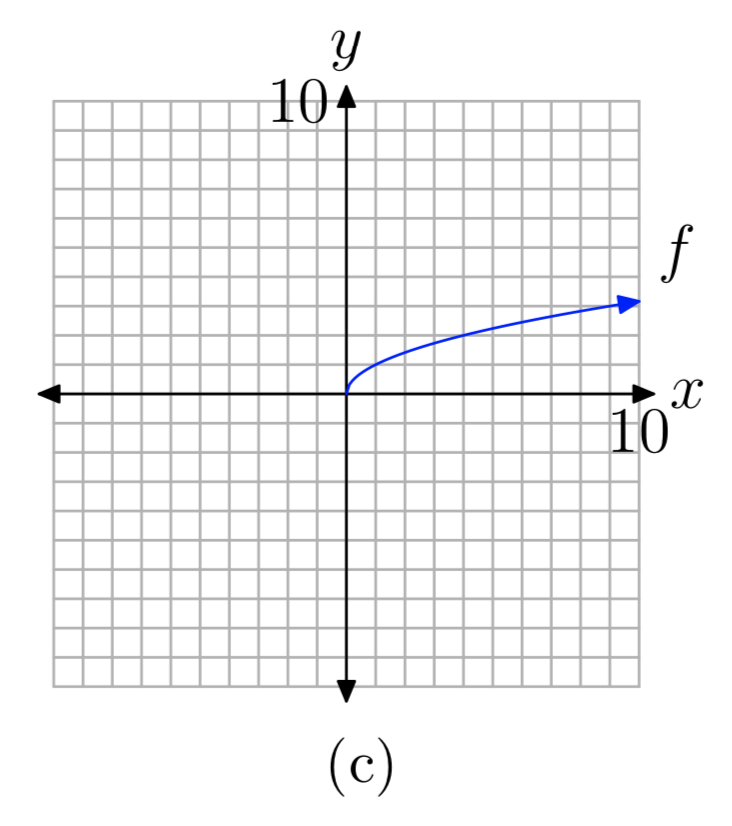
El enfoque de trazado puntual utilizado para dibujar la gráfica de$f(x) = \sqrt{x}$ la Figura 1 es un procedimiento probado y familiar. Sin embargo, un enfoque más sofisticado involucra la teoría de las inversas desarrollada en el capítulo anterior.

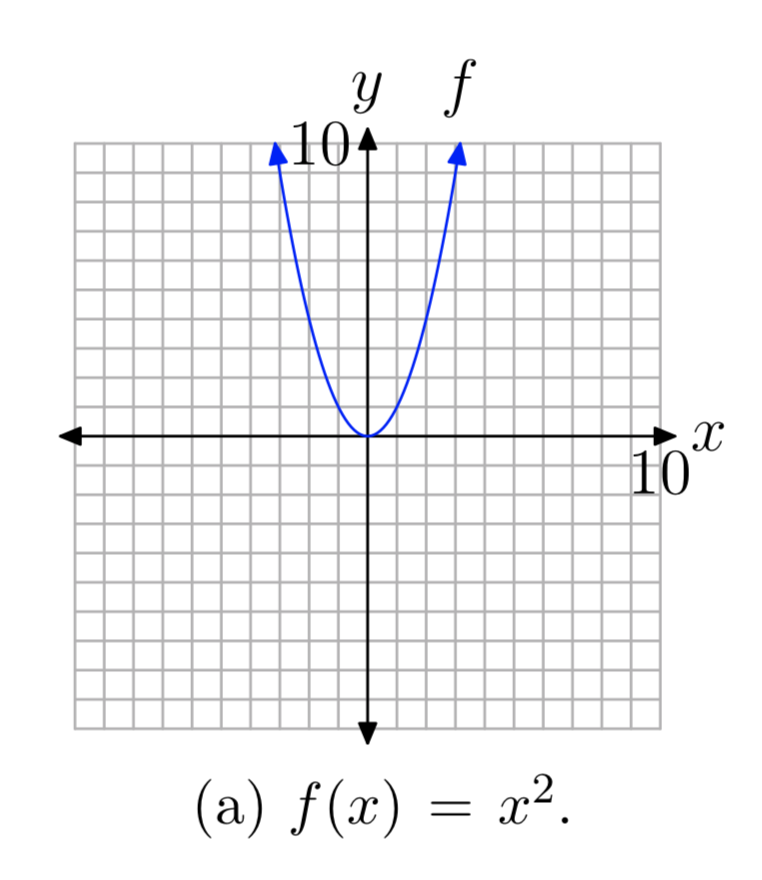
En cierto sentido, tomar la raíz cuadrada es lo “inverso” de la cuadratura. Bueno, no del todo, ya que la función de cuadratura$f(x) = x^2$ en la Figura 2 (a) falla la prueba de línea horizontal y no es uno a uno. Sin embargo, si limitamos el dominio de la función de cuadratura, entonces la gráfica de$f(x) = x^2$ en la Figura 2 (b), donde$x \ge 0$, sí pasa la prueba de línea horizontal y es uno a uno. Por lo tanto, la gráfica de$f(x) = x^2$$x \ge 0$,, tiene una inversa, y la gráfica de su inversa se encuentra reflejando la gráfica de$f(x) = x^2$,$x \ge 0$, a través de la línea y = x (ver Figura 2 (c)).

Screen Shot 2019-05-24 a las 3.22.52 PM.png — Figura 2.} \ text {Dibujando la inversa de} f (x) = x^2, x\ ge 0}\\\ nonumber\ end {array}\]

Screen Shot 2019-05-24 a las 3.22.56 PM.png — Figura 2.} \ text {Dibujando la inversa de} f (x) = x^2, x\ ge 0}\\\ nonumber\ end {array}\]

Para encontrar la ecuación de la inversa, recordemos que el procedimiento requiere que cambiemos los roles de x e y, luego, resolvamos la ecuación resultante para y. Así, primero escribe$f(x) = x^2$,$x \ge 0$, en la forma

\[\begin{array}{c} {y = x^2, x \ge 0}\\ \nonumber \end{array}\]

A continuación, cambie x e y.

\[\begin{array}{c} {x = y^2, y \ge 0}\\ \end{array}\]

Cuando resolvemos esta última ecuación para y, obtenemos dos soluciones,

\[\begin{array}{c} {y = \pm\sqrt{x}}\\ \end{array}\]

Sin embargo, en la ecuación (2), tenga en cuenta que y debe ser mayor o igual a cero. Por lo tanto, debemos elegir la respuesta no negativa en la ecuación (3), por lo que la inversa de$f(x) = x^2$,$x \ge 0$, tiene ecuación

\[\begin{array}{c} {f^{−1}(x) = \sqrt{x}}\\ \nonumber \end{array}\]

Esta es la ecuación de la reflexión de la gráfica de$f(x) = x^2$,$x \ge 0$, que se representa en la Figura 2 (c). Anote la concordancia exacta con la gráfica de la función de raíz cuadrada en la Figura 1 (c).

La secuencia de gráficos en la Figura 2 también nos ayuda a identificar el dominio y el rango de la función de raíz cuadrada.

En la Figura 2 (a), la parábola se abre hacia afuera indefinidamente, tanto a la izquierda como a la derecha. En consecuencia, el dominio es$D_{f} = (−\infty, \infty)$, o todos los números reales. Además, la gráfica tiene vértice en el origen y se abre hacia arriba indefinidamente, por lo que el rango es$R_{f} = [0, \infty)$.
En la Figura 2 (b), restringimos el dominio. Así, la gráfica de$f(x) = x^2$,$x \ge 0$, ahora tiene dominio$D_{f} = [0, \infty)$. El rango no ha cambiado y es$R_{f} = [0, \infty)$.
En la Figura 2 (c), hemos reflejado la gráfica de$f(x) = x^2$,$x \ge 0$, a través de la línea y = x para obtener la gráfica de$f^{−1}(x) = \sqrt{x}$. Debido a que hemos intercambiado el papel de x e y, el dominio de la función raíz cuadrada debe ser igual al rango de$f(x) = x^2$,$x \ge 0$. Es decir,$D_{f^{−1}} =[0,\infty)$ .Del mismo modo, el rango de la función raíz cuadrada debe ser igual al dominio de$f(x) = x^2$,$x \ge 0$. De ahí,$R_{f^{−1}} = [0,\infty)$.

Por supuesto, también podemos determinar el dominio y el rango de la función de raíz cuadrada proyectando todos los puntos de la gráfica sobre los ejes x e y, como se muestra en las Figuras 3 (a) y (b), respectivamente.

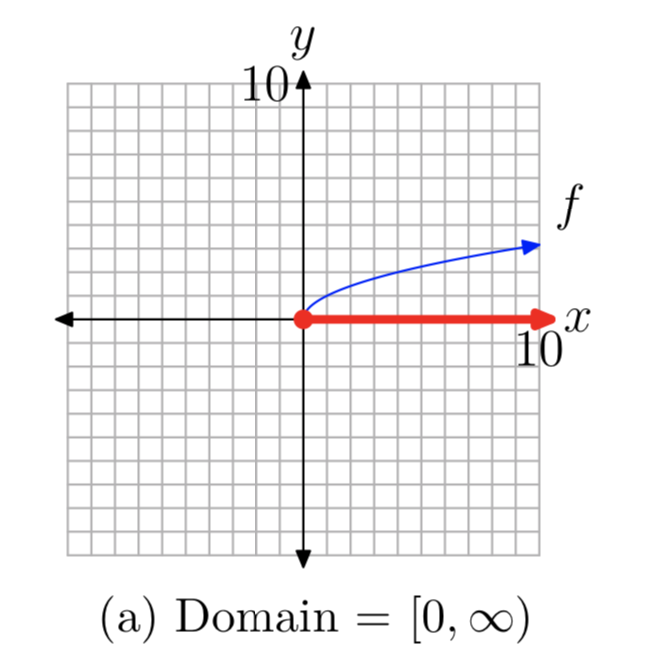
Screen Shot 2019-05-24 a las 3.49.15 PM.png — Figura 3.} \ text {Proyecta a los ejes para encontrar el dominio y el rango}}\\\ nonumber\ end {array}\]

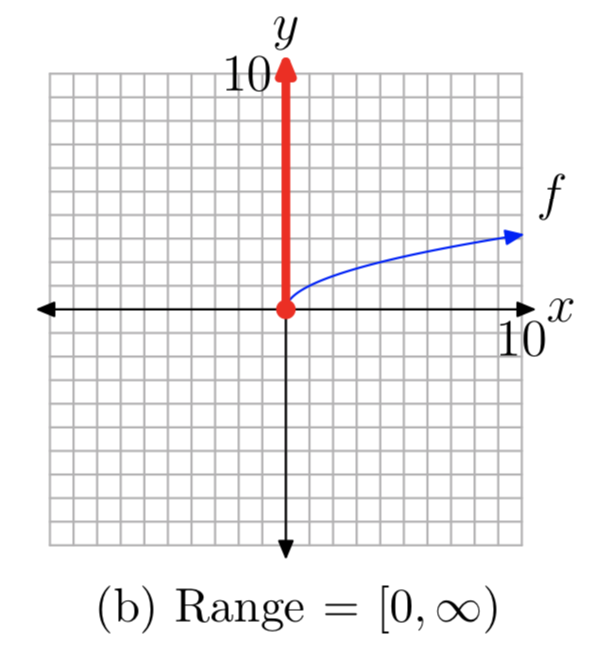
Screen Shot 2019-05-24 a las 3.49.21 PM.png — Figura 3.} \ text {Proyecta a los ejes para encontrar el dominio y el rango}}\\\ nonumber\ end {array}\]

Algunos podrían objetar el rango, preguntando “¿Cómo sabemos que la gráfica de la imagen de la función raíz cuadrada en la Figura 3 (b) se eleva indefinidamente?” Nuevamente, la respuesta está en la secuencia de gráficas de la Figura 2. En la Figura 2 (c), tenga en cuenta que la gráfica de$f(x) = x^2$,$x \ge 0$, se abre indefinidamente a la derecha a medida que la gráfica se eleva hasta el infinito. De ahí que después de reflejar esta gráfica a través de la línea y = x, la gráfica resultante debe elevarse indefinidamente hacia arriba a medida que se mueve hacia la derecha. Así, el rango de la función de raíz cuadrada es$[0, \infty)$.

Traducciones

Si desplazamos la gráfica de$y = \sqrt{x}$ derecha e izquierda, o arriba y abajo, el dominio y/o rango se ven afectados.

Ejemplo$\PageIndex{4}$

Esbozar la gráfica de$f(x) = \sqrt{x−2}$. Usa tu gráfica para determinar el dominio y el rango.

Sabemos que la ecuación básica$y=\sqrt{x}$ tiene la gráfica mostrada en las Figuras 1 (c). Si reemplazamos x por x − 2, la ecuación básica$y=\sqrt{x}$ becomes $f(x) = \sqrt{x−2}$. De nuestro trabajo anterior con transformaciones geométricas, sabemos que esto desplazará la gráfica dos unidades hacia la derecha, como se muestra en las Figuras 4 (a) y (b).

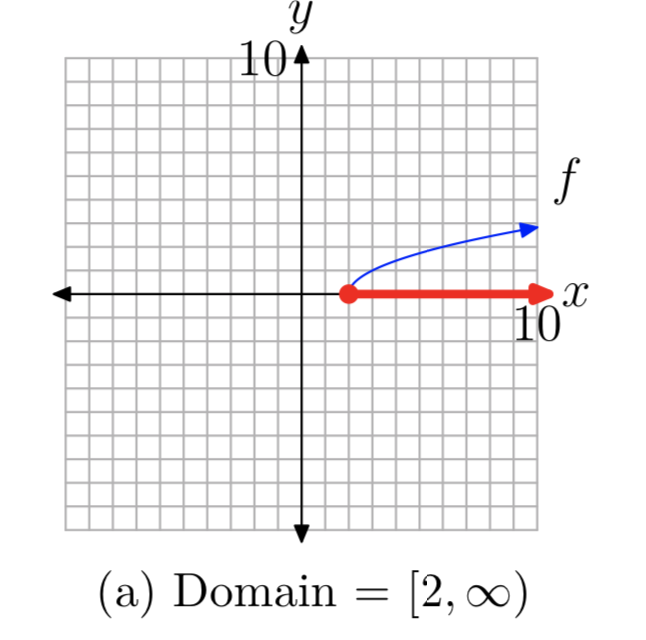
Screen Shot 2019-05-24 a las 4.00.39 PM.png — Figura 4. Para dibujar la gráfica de la$f(x) = \sqrt{x−2}$, desplazar la gráfica de$y=\sqrt{x}$ two units to the right.

Screen Shot 2019-05-24 a las 4.00.47 PM.png — Figura 4. Para dibujar la gráfica de la$f(x) = \sqrt{x−2}$, desplazar la gráfica de$y=\sqrt{x}$ two units to the right.

Para encontrar el dominio, proyectamos cada punto de la gráfica de f sobre el eje x, como se muestra en la Figura 4 (a). Tenga en cuenta que todos los puntos a la derecha de o incluyendo 2 están sombreados en el eje x. En consecuencia, el dominio de f es

Dominio =$[2, \infty)$ = {x:$x \ge 0$}

Como no ha habido ningún desplazamiento en la dirección vertical, el rango sigue siendo el mismo. Para encontrar el rango, proyectamos cada punto de la gráfica sobre el eje y, como se muestra en la Figura 4 (b). Tenga en cuenta que todos los puntos en y por encima de cero están sombreados en el eje y. Por lo tanto, el rango de f es

Rango =$[0,\infty)$ = {y:$y \ge 0$}.

Podemos encontrar el dominio de esta función algebraicamente examinando su ecuación definitoria$f(x) = \sqrt{x−2}$. Entendemos que no podemos tomar la raíz cuadrada de un número negativo. Por lo tanto, la expresión bajo el radical debe ser no negativa (positiva o cero). Es decir,

$x − 2 \ge 0$.

Resolviendo esta desigualdad para x,

$x \ge 2$.

Así, el dominio de f es Domain =$[2, \infty)$, que coincide con la solución gráfica anterior.

Veamos otro ejemplo.

Ejemplo$\PageIndex{5}$

Esbozar la gráfica de$f (x) = \sqrt{x + 4} + 2$. Utilice su gráfica para determinar el dominio y el rango de f.

Nuevamente, sabemos que la ecuación básica$y=\sqrt{x}$ tiene la gráfica que se muestra en la Figura 1 (c). Si reemplazamos x por x +4, la ecuación básica$y=\sqrt{x}$ se vuelve$y=\sqrt{x+4}$. De nuestro trabajo anterior con transformaciones geométricas, sabemos que esto desplazará la gráfica de$y=\sqrt{x}$ cuatro unidades hacia la izquierda, como se muestra en la Figura 5 (a).

Si sabemos sumar 2 a la ecuación$y=\sqrt{x+4}$ para producir la ecuación$y=\sqrt{x+4} + 2$, esto desplazará la gráfica de$y=\sqrt{x+4}$ dos unidades hacia arriba, como se muestra en la Figura 5 (b).

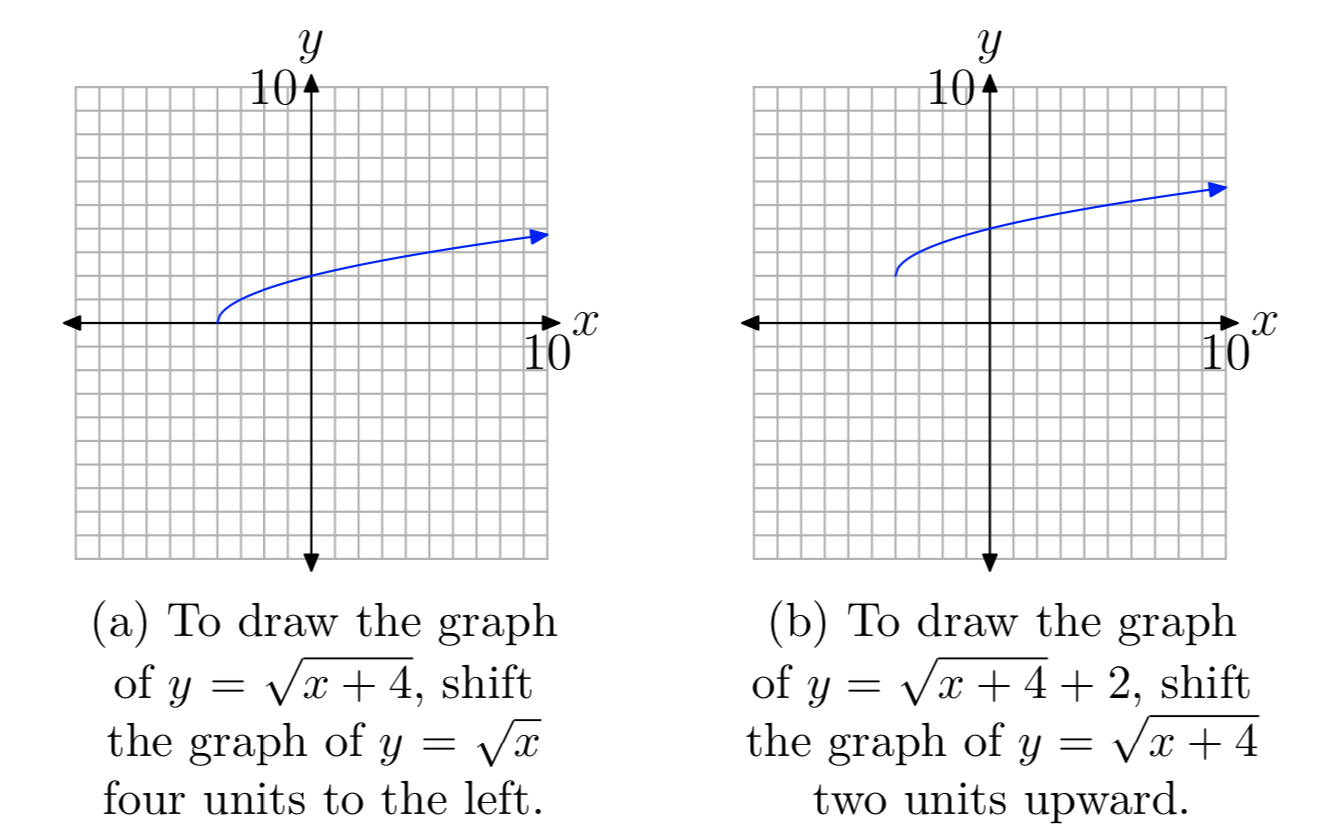
Screen Shot 2019-06-14 a las 3.41.30 PM.png — Figura 5. Traduciendo la ecuación original$y = \sqrt{x}$ para obtener la gráfica de$y = \sqrt{x+4} + 2$

Para identificar el dominio th del$f (x) = \sqrt{x + 4} + 2$, proyectamos todos los puntos de la gráfica de f sobre el eje x, como se muestra en la Figura 6 (a). Tenga en cuenta que todos los puntos a la derecha o incluyendo − 4 están sombreados en el eje x. Así, el dominio de$f (x) = \sqrt{x + 4} + 2$ es

Dominio =$[−4, \infty)$ = {x:$x \ge −4$}

Figura 6. Proyectar puntos de f sobre los ejes para determinar el dominio y el rango

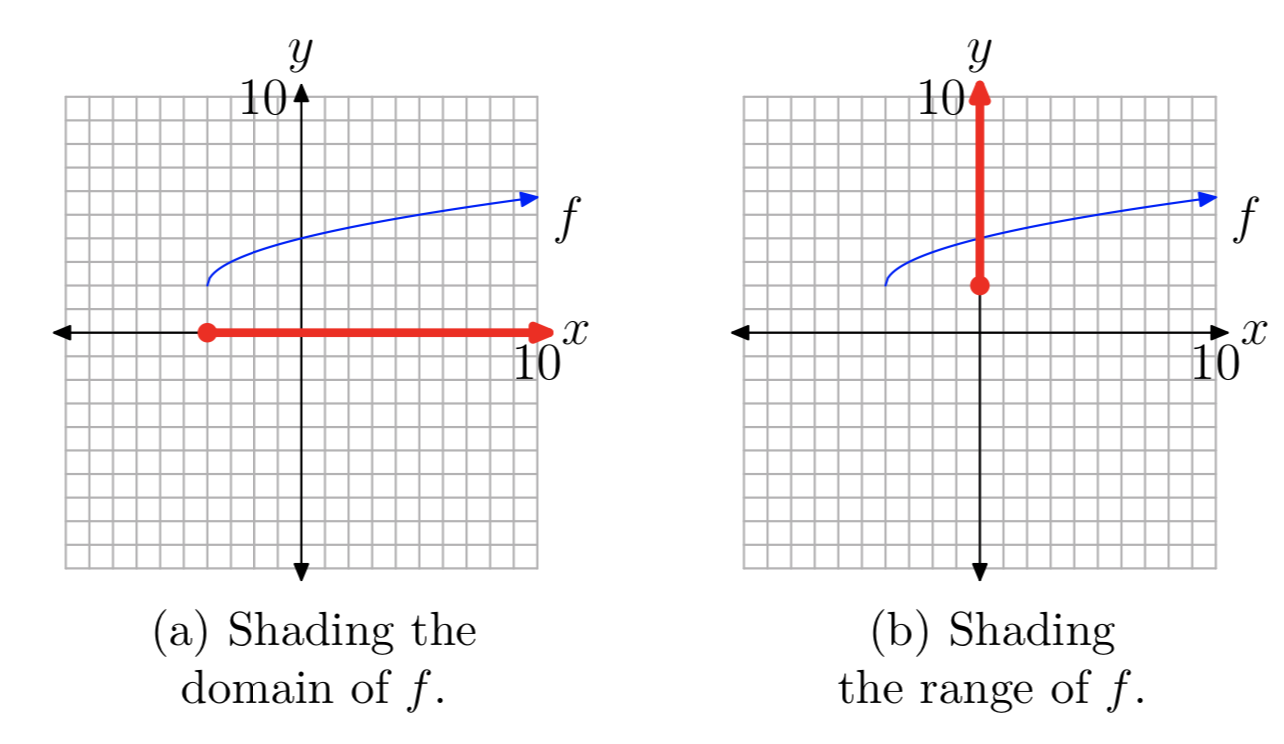
Screen Shot 2019-06-14 a las 3.42.09 PM.png — Figura 6. Proyectar puntos de f sobre los ejes para determinar el dominio y el rango

De igual manera, para encontrar el rango de f, proyectar todos los puntos de la gráfica de f sobre el eje y, como se muestra en la Figura 6 (b). Tenga en cuenta que todos los puntos en el eje y mayores que o incluyendo 2 están sombreados. En consecuencia, el rango de f es

Rango =$[2, \infty)$ = {y:$y \ge 2$}

También podemos encontrar el dominio de f algebraicamente examinando la ecuación$f (x) = \sqrt{x + 4} + 2$. No podemos tomar la raíz cuadrada de un número negativo, por lo que la expresión bajo el radical debe ser no negativa (cero o positiva). En consecuencia,

$x + 4 \ge 0$.

Resolviendo esta desigualdad para x,

$x \ge −4$.

Así, el dominio de f es Domain =$[−4,\infty)$, el cual coincide con la solución gráfica presentada anteriormente.

Reflexiones

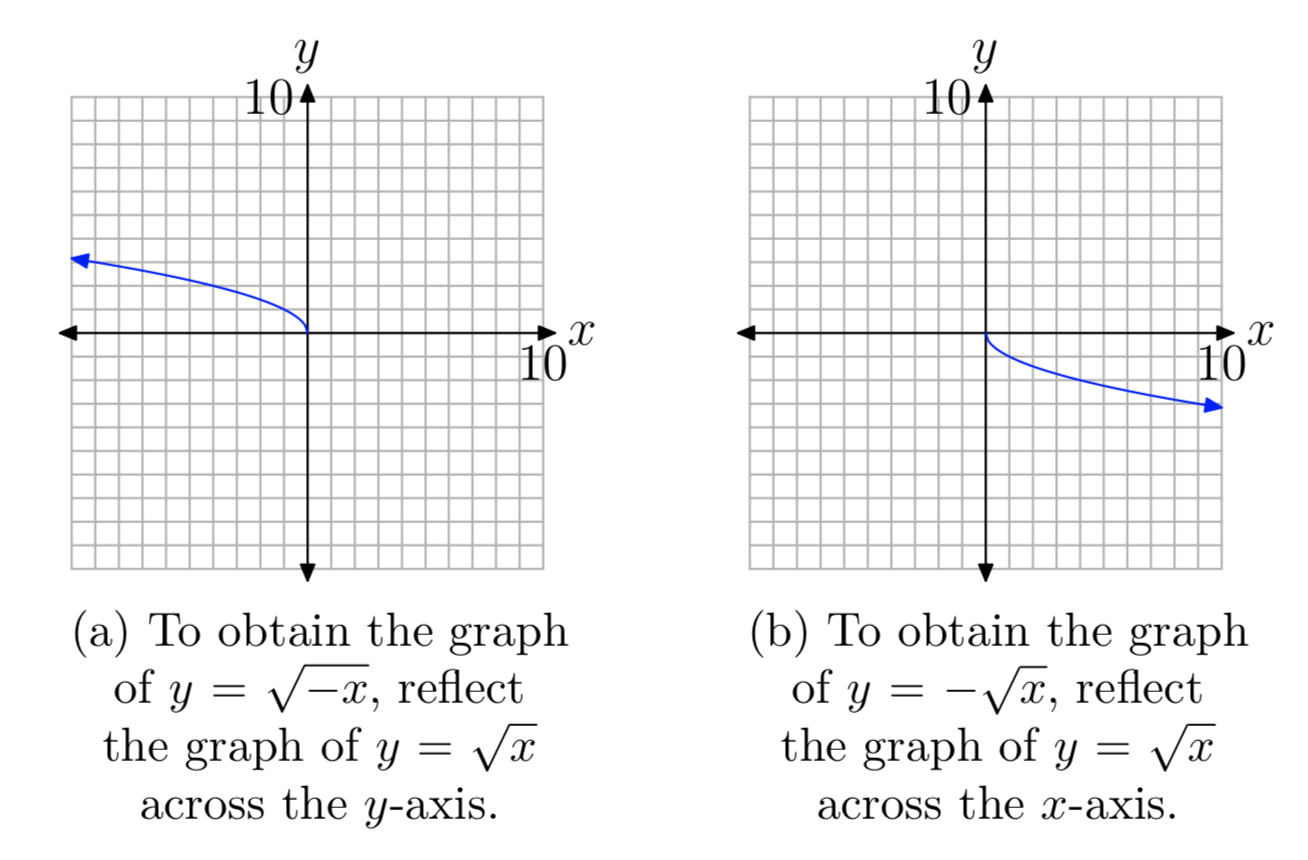
Si comenzamos con la ecuación básica$y = \sqrt{x}$, luego reemplazamos x por −x, entonces la gráfica de la ecuación resultante$y = \sqrt{−x}$ se captura reflejando la gráfica de$y = \sqrt{x}$ (ver Figura 1 (c)) horizontalmente a través del eje y. La gráfica de$y = \sqrt{−x}$ se muestra en la Figura 7 (a).

De igual manera, la gráfica de$y = −\sqrt{x}$ sería una reflexión vertical de la gráfica de$y = \sqrt{x}$ a través del eje x, como se muestra en la Figura 7 (b).

Screen Shot 2019-06-14 a las 3.43.13 PM.png — Figura 7. Reflejando la gráfica de$y = \sqrt{x}$ a través de los ejes x e y.

La mayor parte de las veces, se te pedirá que realices una reflexión y una traducción.

Ejemplo$\PageIndex{6}$

Esbozar la gráfica de$f(x) = \sqrt{4− x}$. Utilice la gráfica resultante para determinar el dominio y el rango de f.

Primero, reescribe la ecuación de la$f(x) = \sqrt{4− x}$ siguiente manera:

$f(x) = \sqrt{−(x−4)}$

Definición

Reflexiones Primero. Por lo general, es más intuitivo realizar reflexiones antes de las traducciones.

Con este pensamiento en mente, primero esbozamos la gráfica de$f(x) = \sqrt{−x}$, que es un reflejo de la gráfica de$f(x) = \sqrt{x}$ a través del eje y. Esto se muestra en la Figura 8 (a).

Ahora, en$f(x) = \sqrt{−x}$ reemplazar x por x − 4 para obtener$f(x) = \sqrt{−(x−4)}$. Esto desplaza la gráfica de$f(x) = \sqrt{−x}$ f nuestras unidades hacia la derecha, como se muestra en la Figura 8 (b).

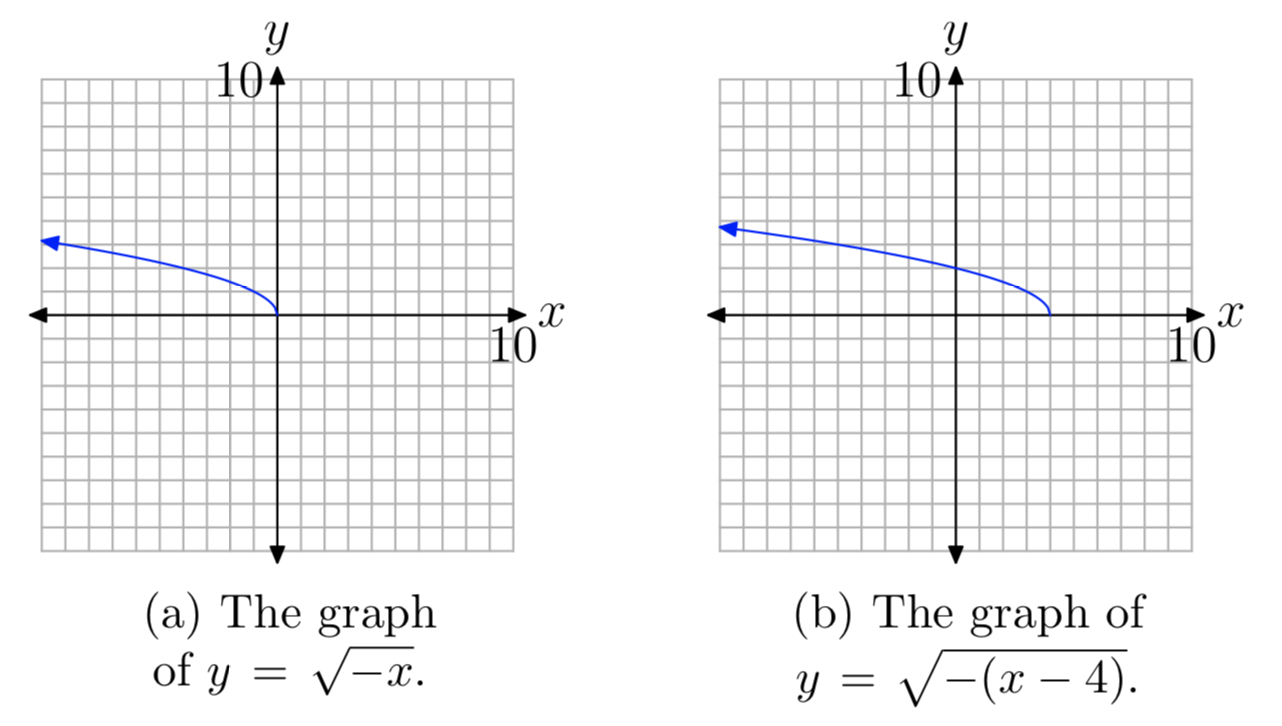
Screen Shot 2019-06-14 a las 3.45.43 PM.png — Figura 8. Una reflexión seguida de una traducción.

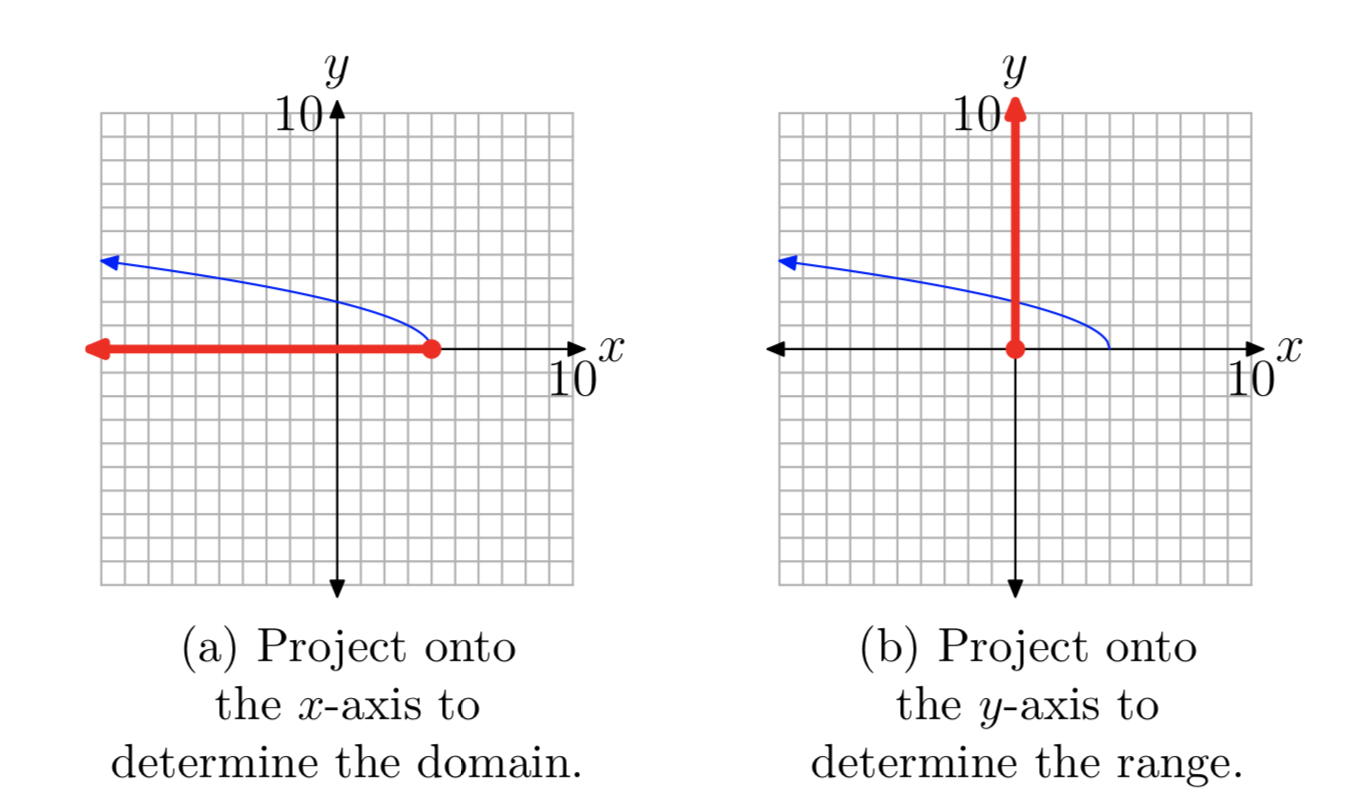
Para encontrar el dominio de la función$f(x) = \sqrt{−(x−4)}$, o equivalentemente$f(x) = \sqrt{4−x}$, proyectar cada punto de la gráfica de f sobre el eje x, como se muestra en la Figura 9 (a). Tenga en cuenta que todos los números reales menores o iguales a 4 están sombreados en el eje x. Por lo tanto, el dominio de f es

Dominio =$(−\infty, 4]$ = {x:$x \le 4$}.

De igual manera, para obtener el rango de f, proyectar cada punto de la gráfica de f sobre el eje, como se muestra en la Figura 9 (b). Tenga en cuenta que todos los números reales mayores o iguales a cero están sombreados en el eje y. Por lo tanto, el rango de f es

Rango =$[0,\infty)$ = {x:$x \ge 0$}.

También podemos encontrar el dominio de la función f examinando la ecuación$f(x) = \sqrt{4−x}$. No podemos tomar la raíz cuadrada de un número negativo, por lo que la expresión bajo el radical debe ser no negativa (cero o positiva). En consecuencia,

$4 − x \ge 0$.

Screen Shot 2019-06-14 a las 3.46.52 PM.png — Figura 9. Determinar el dominio y el rango de$f(x) = \sqrt{4−x}$

Resolver esta última desigualdad para x. Primero resta 4 de ambos lados de la desigualdad, luego multiplica ambos lados de la desigualdad resultante por − 1. Por supuesto, multiplicar por un número negativo invierte el símbolo de desigualdad.

$−x \ge −4$

$x \le 4$

Así, el dominio de f es {x:$x \le 4$}. En notación de intervalos, Dominio =$(−\infty, 4]$. Esto concuerda muy bien con el resultado gráfico que se encuentra arriba.

La mayoría de las veces, tomará una combinación de su calculadora gráfica y un poco de manipulación algebraica para determinar el dominio de una función de raíz cuadrada.

Ejemplo$\PageIndex{7}$

Esbozar la gráfica de$f(x) = \sqrt{5−2x}$ Utilizar la gráfica y una técnica algebraica para determinar el dominio de la función.

Cargue la función en Y1 en el menú Y= de su calculadora, como se muestra en la Figura 10 (a). Seleccione 6: ZStandard en el menú ZOOM para producir la gráfica que se muestra en la Figura 10 (b).

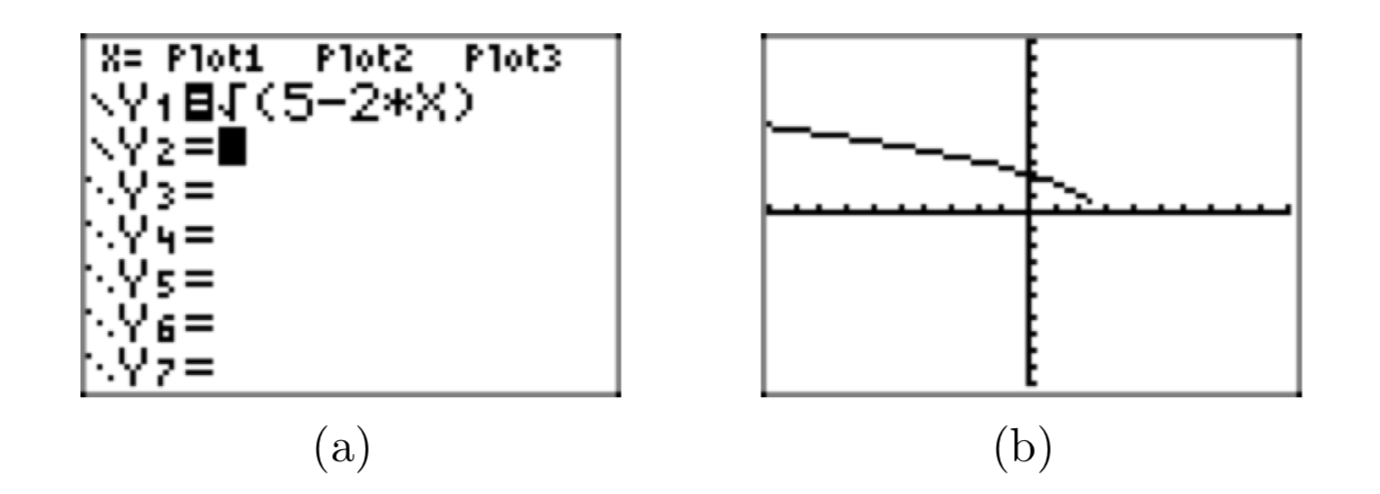
Screen Shot 2019-06-14 a las 3.48.53 PM.png — Figura 10. Dibujando la gráfica de f (x) =\ sqrt {5−2x} en la calculadora gráfica.

Observe cuidadosamente la gráfica de la Figura 10 (b) y tenga en cuenta que es difícil saber si la gráfica llega hasta el final para “tocar” el eje x cerca$x \approx 2.5$. Sin embargo, nuestra experiencia previa con la función de raíz cuadrada nos hace creer que esto es solo un artefacto de resolución insuficiente en la calculadora que está impidiendo que la gráfica “toque” el eje x en$x \approx 2.5$.

Un enfoque algebraico resolverá el tema. Podemos determinar el dominio de f examinando la ecuación$f(x) = \sqrt{5 − 2x}$. En consecuencia, no podemos tomar la raíz cuadrada de un número negativo, por lo que la expresión bajo el radical debe ser no negativa (cero o positiva).

$5 − 2x \ge 0$.

Resolver esta última desigualdad para x. Primero, restar 5 de ambos lados de la desigualdad.

$−2x \ge −5$.

A continuación, dividir ambos lados de esta última desigualdad por −2. Recuerda que debemos revertir la desigualdad en el momento en que dividimos por un número negativo.

$\frac{−2x}{−2} \le \frac{−5}{−2}$.

$x \le \frac{5}{2}$.

Así, el dominio de f es {x:$x \le \frac{5}{2}$}. En notación de intervalos, Dominio =$(−\infty, \frac{5}{2}]$. Esto concuerda muy bien con el resultado gráfico que se encuentra arriba.

Una mayor introspección revela que este argumento también resuelve la cuestión de si la gráfica “toca” o no el eje x en$x= \frac{5}{2}$. Si no estás convencido, entonces sustituya$x=\frac{5}{2}$$f(x) = \sqrt{5−2x}$ para ver

$f(\frac{5}{2})= \sqrt{5−2(\frac{5}{2})} =\sqrt{0} = 0$.

Así, la gráfica de f “toca” el eje x en el punto$(\frac{5}{2}, 0)$.

En el Ejercicio 1-10, complete cada una de las siguientes tareas:

Configure un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje.
Completar la tabla de puntos para la función dada. Trace cada uno de los puntos en su sistema de coordenadas, luego utilícelos para ayudar a dibujar la gráfica de la función dada.
Usa lápices de diferentes colores para proyectar todos los puntos en los ejes x e y para determinar el dominio y el rango. Utilice la notación de intervalos para describir el do- main de la función dada.

Ejercicio$\PageIndex{1}$

$f(x) = −\sqrt{x}$

x	0	1	4	9
f (x)

Contestar

x	0	1	4	9
f (x)	0	− 1	− 2	− 3

Traza los puntos en la tabla y úsalos para ayudar a dibujar la gráfica.

$Screen Shot 2019-05-28 a las 11.25.20 PM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$[0, \infty)$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$(−\infty, 0]$.

Ejercicio$\PageIndex{2}$

$f(x) = \sqrt{−x}$

x	0	− 1	− 4	− 9
f (x)

Ejercicio$\PageIndex{3}$

$f(x)= \sqrt{x+2}$

x	− 2	− 1	2	7
f (x)

Contestar

x	− 2	− 1	2	7
f (x)	0	1	2	3

Traza los puntos en la tabla y úsalos para ayudar a dibujar la gráfica.

$Screen Shot 2019-05-28 a las 11.29.25 PM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$[−2, \infty)$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$[0, \infty)$.

Ejercicio$\PageIndex{4}$

$f(x)= \sqrt{5−x}$

x	− 4	1	4	5
f (x)

Ejercicio$\PageIndex{5}$

$f(x)= \sqrt{x}+2$

x	0	1	4	9
f (x)

Contestar

x	0	1	4	9
f (x)	2	3	4	5

Trace los puntos en la tabla y utilícelos para dibujar la gráfica de f.

$Screen Shot 2019-05-28 a las 11.33.13 PM.png$

Ejercicio$\PageIndex{6}$

$f(x)=\sqrt{x}−1$

x	0	1	4	9
f (x)

Ejercicio$\PageIndex{7}$

$f(x)= \sqrt{x+3}+2$

x	− 3	− 2	1	6
f (x)

Contestar

x	− 3	− 2	1	6
f (x)	2	3	4	5

Trace los puntos en la tabla y utilícelos para dibujar la gráfica de f.

$Screen Shot 2019-05-28 a las 11.38.27 PM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$[−3, \infty)$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$[2, \infty)$.

Ejercicio$\PageIndex{8}$

$f(x)= \sqrt{x−1}+3$

x	1	2	5	10
f (x)

Ejercicio$\PageIndex{9}$

$f(x)= \sqrt{3−x}$

x	− 6	− 1	2	3
f (x)

Contestar

x	− 6	− 1	2	3
f (x)	3	2	1	0

Trace los puntos en la tabla y utilícelos para dibujar la gráfica de f.

$Screen Shot 2019-05-28 a las 11.42.01 PM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$(−\infty, 3]$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$[0, \infty)$.

Ejercicio$\PageIndex{10}$

$f(x)=−\sqrt{x+3}$

x	− 3	− 2	1	6
f (x)

En Ejercicios 11 - 20, realice cada una de las siguientes tareas.

Configure un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
Utilice transformaciones geométricas para dibujar la gráfica de la función dada en su sistema de coordenadas sin el uso de una calculadora gráfica. Nota: Puede verificar su solución con su calculadora, pero debería poder producir el gráfico sin el uso de su calculadora.
Usa lápices de diferentes colores para proyectar los puntos de la gráfica de la función sobre los ejes x e y. Utilice la notación de intervalos para describir el dominio y el rango de la función.

Ejercicio$\PageIndex{11}$

$f(x)= \sqrt{x}+3$

Contestar

Primero, graficar la gráfica de$y = \sqrt{x}$, como se muestra en (a). Después, suma 3 para producir la ecuación$y = \sqrt{x} + 3$. Esto desplazará la gráfica de 3 unidades$y = \sqrt{x}$ ascendentes, como se muestra en (b).

$Screen Shot 2019-05-28 a las 11.50.22 PM.png$

$Screen Shot 2019-05-29 a las 10.35.29 AM.png$

Ejercicio$\PageIndex{12}$

$f(x)=\sqrt{x+3}$

Ejercicio$\PageIndex{13}$

$f(x)=\sqrt{x−2}$

Contestar

Primero, graficar la gráfica de$y = \sqrt{x}$, como se muestra en (a). Luego, reemplace x por x − 2 para producir la ecuación$y = \sqrt{x−2}$. Esto desplazará la gráfica de$y = \sqrt{x}$ a la derecha 2 unidades, como se muestra en (b).

$Screen Shot 2019-05-29 a las 10.20.45 AM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$[2, \infty)$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$[0, \infty)$.

$Screen Shot 2019-05-29 a las 10.35.43 AM.png$

Ejercicio$\PageIndex{14}$

$f(x)=\sqrt{x}−2$

Ejercicio$\PageIndex{15}$

$f(x)= \sqrt{x+5}+1$

Contestar

Primero, graficar la gráfica de$y = \sqrt{x}$, como se muestra en (a). Después, reemplace x por x + 5 para producir la ecuación$y = \sqrt{x+5}$. Luego agrega 1 para producir la ecuación$f(x)= \sqrt{x+5}+1$. Esto desplazará la gráfica de$y = \sqrt{x}$ hacia la izquierda 5 unidades, luego hacia arriba 1 unidad, como se muestra en (b).

$Screen Shot 2019-05-29 a las 10.26.37 AM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$[−5, \infty)$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$[1, \infty)$.

$Screen Shot 2019-05-29 a las 10.36.25 AM.png$

Ejercicio$\PageIndex{16}$

$f(x)=\sqrt{x−2}−1$

Ejercicio$\PageIndex{17}$

$y = −\sqrt{x + 4}$

Contestar

Primero, graficar la gráfica de$y = \sqrt{x}$, como se muestra en (a). Entonces, negar para producir el$y = −\sqrt{x}$. Esto reflejará la gráfica de$y = \sqrt{x}$ a través del eje x como se muestra en (b). Finalmente, reemplace x por x + 4 para producir la ecuación$y = −\sqrt{x + 4}$. Esto desplazará la gráfica de$y = −\sqrt{x}$ cuatro unidades hacia la izquierda, como se muestra en (c).

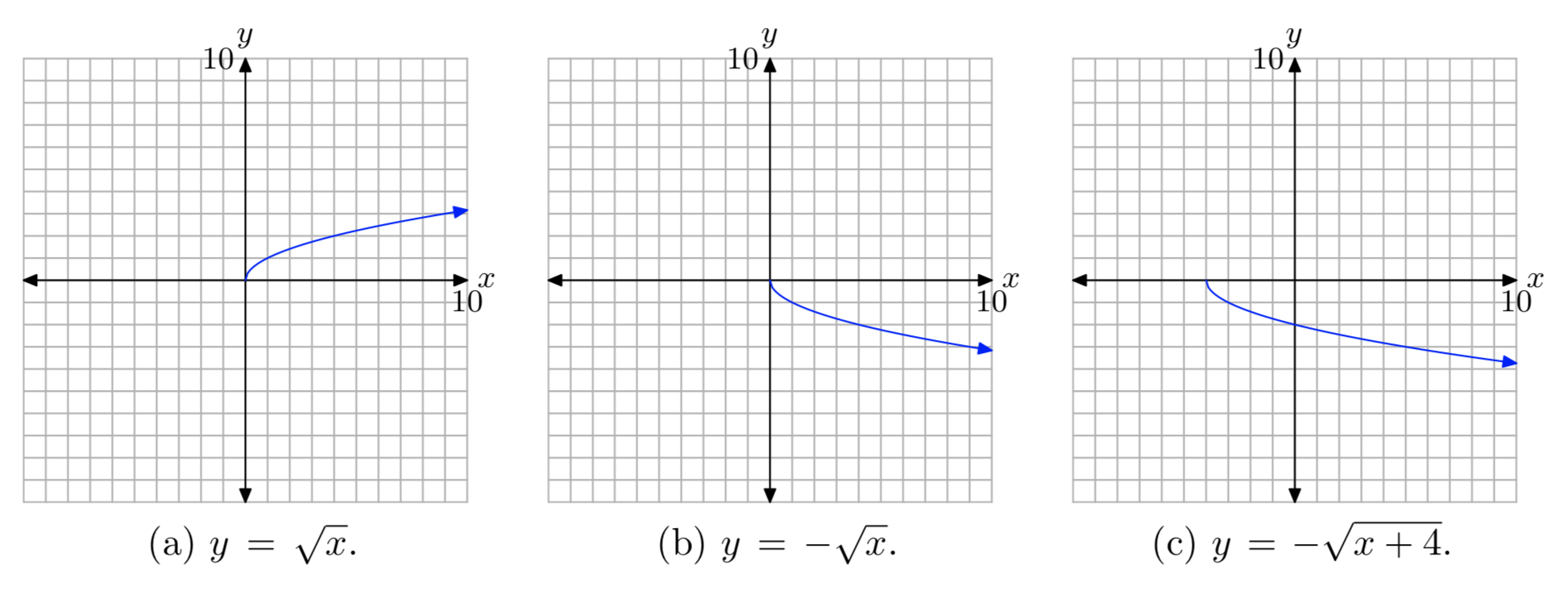
$Screen Shot 2019-05-29 a las 10.41.03 AM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$[−4, \infty)$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$(−\infty, 0]$.

$Screen Shot 2019-05-29 a las 10.36.47 AM.png$

Ejercicio$\PageIndex{18}$

$f(x)=−\sqrt{x}+4$

Ejercicio$\PageIndex{19}$

$f(x)=−\sqrt{x}+3$

Contestar

Primero, graficar la gráfica de$y = \sqrt{x}$, como se muestra en (a). Entonces, negar para producir el$y = −\sqrt{x}$. Esto reflejará la gráfica de$y = \sqrt{x}$ a través del eje x como se muestra en (b). Finalmente, sumar 3 para producir la ecuación$y=−\sqrt{x}+3$. Esto desplazará la gráfica de$y = −\sqrt{x}$ tres unidades hacia arriba, como se muestra en (c).

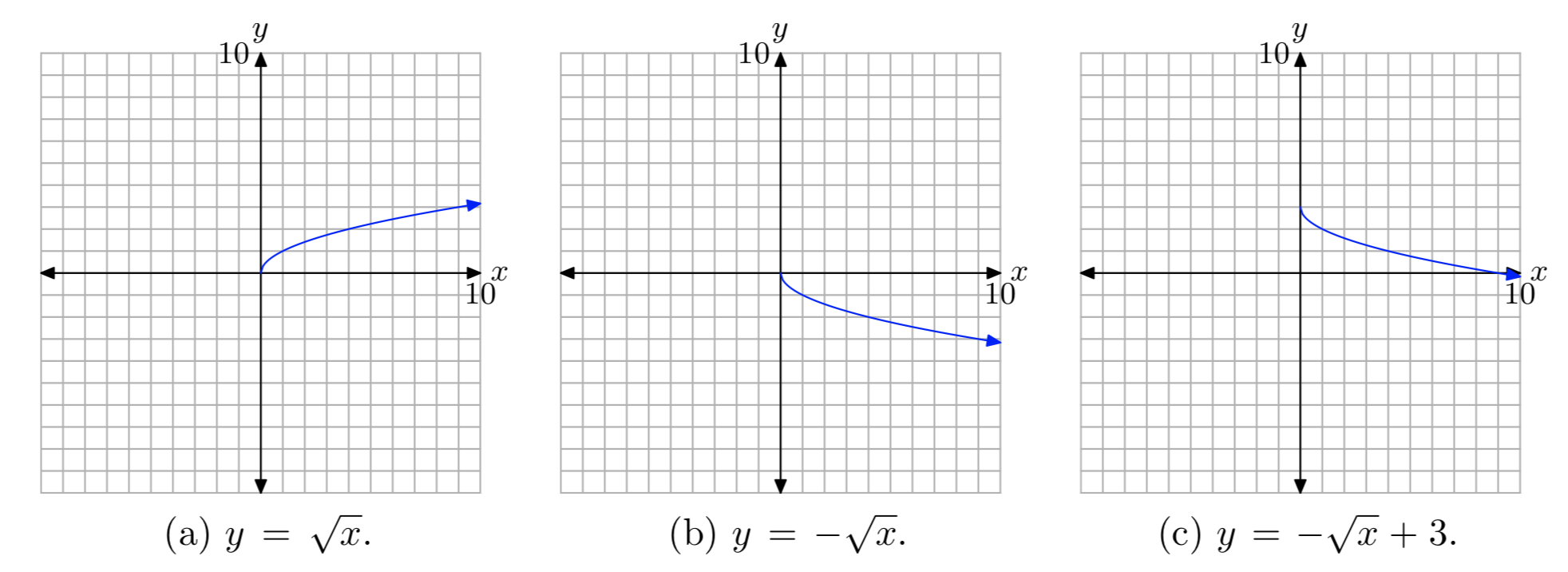
$Screen Shot 2019-05-29 a las 11.35.50 AM.png$

$Screen Shot 2019-05-29 a las 11.39.11 AM.png$

Ejercicio$\PageIndex{20}$

$f(x)=−\sqrt{x+3}$

Ejercicio$\PageIndex{21}$

Para dibujar la gráfica de la función$f(x) = \sqrt{3−x}$, realice cada uno de los siguientes pasos en secuencia sin la ayuda de una calculadora.

Configure un sistema de coordenadas y esboce la gráfica de$y = \sqrt{x}$. Etiquete la gráfica con su ecuación.
Configure un segundo sistema de coordenadas y esboce la gráfica de$y = \sqrt{−x}$. Etiquete la gráfica con su ecuación.
Configure un tercer sistema de coordenadas y esboce la gráfica de$y =\sqrt{−(x − 3)}$. Etiquete la gráfica con su ecuación. Esta es la gráfica de$y =\sqrt{3−x}$. Utilice la notación de intervalos para indicar el dominio y el rango de esta función.

Contestar

Primero, graficar la gráfica de$y = \sqrt{x}$, como se muestra en (a). Luego, reemplace x por − x para producir la ecuación$y = \sqrt{−x}$. Esto reflejará la gráfica de$y = \sqrt{x}$ a través del eje y, como se muestra en (b). Finalmente, reemplace x por x − 3 para producir la ecuación$y = \sqrt{−(x − 3)}$. Esto desplazará la gráfica de$y = \sqrt{−x}$ tres unidades hacia la derecha, como se muestra en (c).

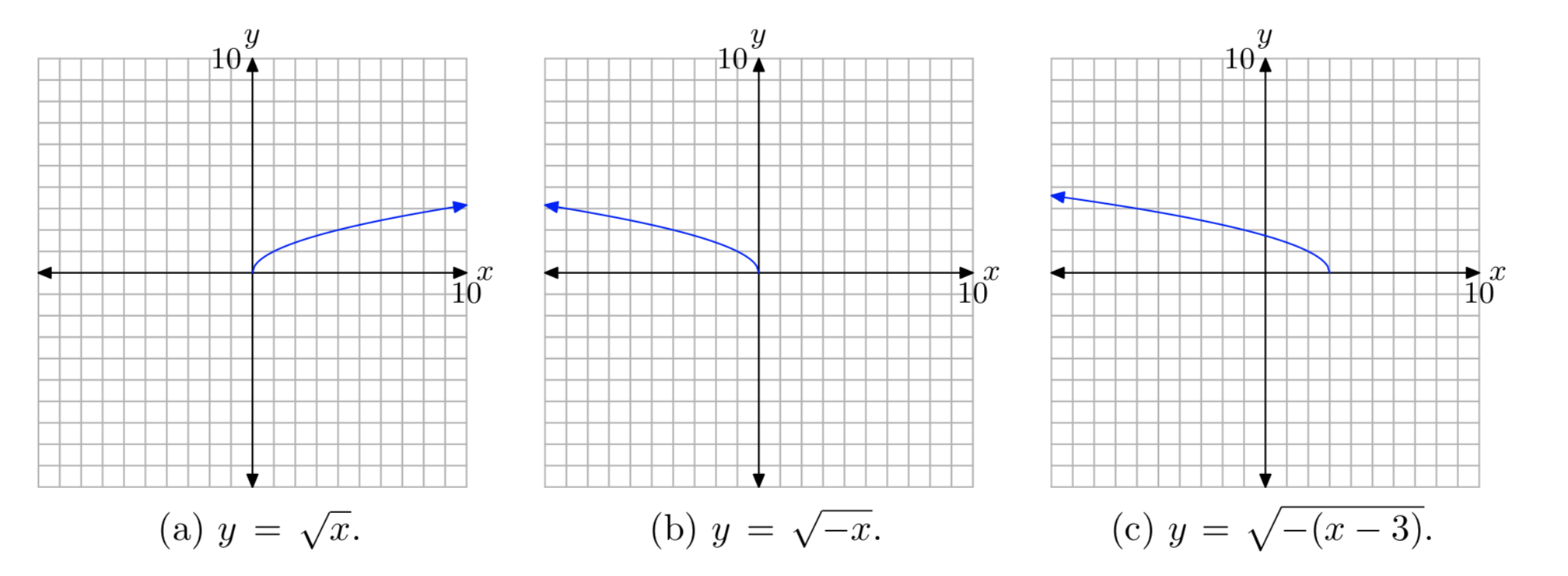
$Screen Shot 2019-05-29 a las 11.51.00 AM.png$

$Screen Shot 2019-05-29 a las 11.52.37 AM.png$

Ejercicio$\PageIndex{22}$

Para dibujar la gráfica de la función$f(x) = \sqrt{−x−3}$, realice cada uno de los siguientes pasos en secuencia.

Configure un sistema de coordenadas y esboce la gráfica de$y = \sqrt{x}$. Etiquete la gráfica con su ecuación.
Configure un segundo sistema de coordenadas y esboce la gráfica de$y = \sqrt{−x}$. Etiquete la gráfica con su ecuación.
Configure un tercer sistema de coordenadas y esboce la gráfica de$y =\sqrt{−(x + 3)}$. Etiquete la gráfica con su ecuación. Esta es la gráfica de$y =\sqrt{−x−3}$. Utilice la notación de intervalos para indicar el dominio y el rango de esta función.

Ejercicio$\PageIndex{23}$

Para dibujar la gráfica de la función$f(x) = \sqrt{−x−3}$, realice cada uno de los siguientes pasos en secuencia sin la ayuda de una calculadora.

Configure un sistema de coordenadas y esboce la gráfica de$y = \sqrt{x}$. Etiquete la gráfica con su ecuación.
Configure un segundo sistema de coordenadas y esboce la gráfica de$y = \sqrt{−x}$. Etiquete la gráfica con su ecuación.
Configure un tercer sistema de coordenadas y esboce la gráfica de$y =\sqrt{−(x + 1)}$. Etiquete la gráfica con su ecuación. Esta es la gráfica de$y =\sqrt{−x−1}$. Utilice la notación de intervalos para indicar el dominio y el rango de esta función.

Contestar

Primero, graficar la gráfica de$y = \sqrt{x}$, como se muestra en (a). Luego, reemplace x por −x para producir la ecuación$y = \sqrt{−x}$. Esto reflejará la gráfica de$y = \sqrt{x}$ a través del eje y, como se muestra en (b). Finalmente, reemplace x por x + 1 para producir la ecuación$y = \sqrt{−(x + 1)}$. Esto desplazará la gráfica de$y = \sqrt{−x}$ una unidad hacia la izquierda, como se muestra en (c).

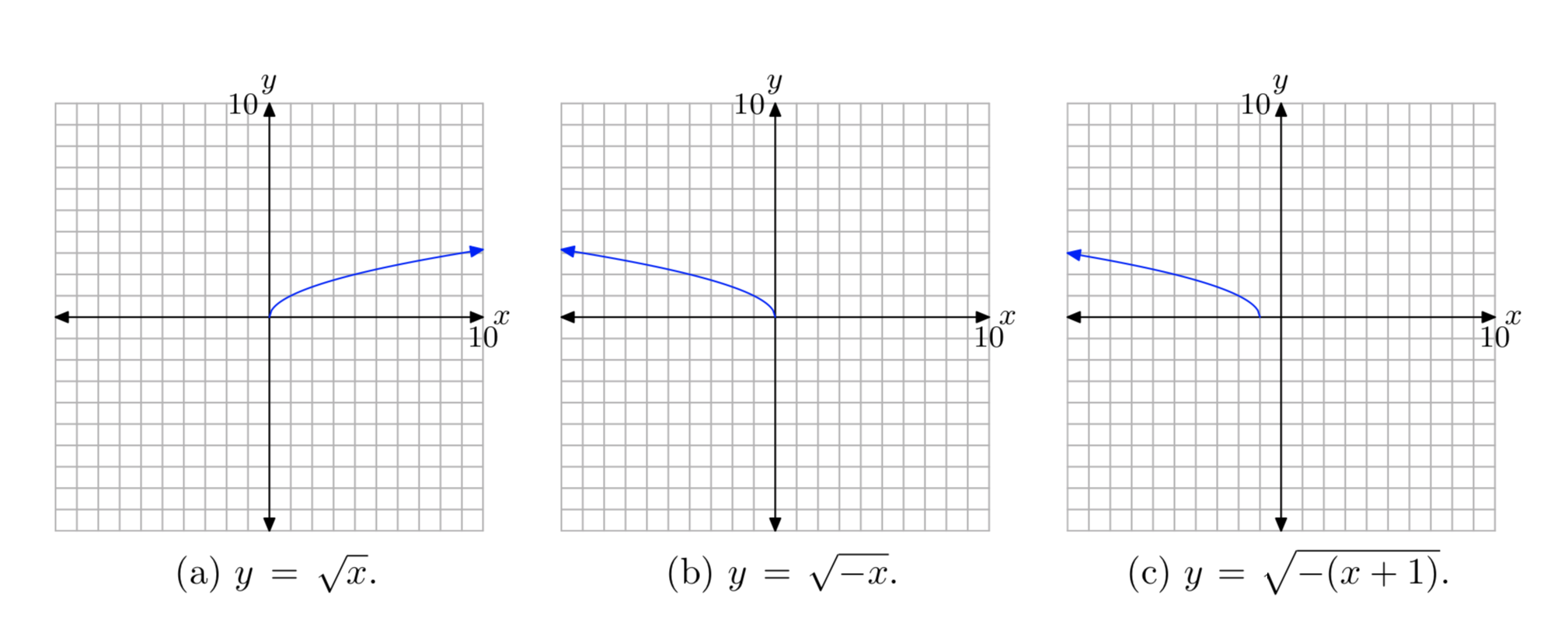
$Screen Shot 2019-05-29 a las 2.19.49 PM.png$

Proyecte todos los puntos de la gráfica en el eje x para determinar el dominio: Dominio =$(−\infty, −1]$. Proyecte todos los puntos de la gráfica sobre el eje y para determinar el rango: Rango =$[0, \infty)$.

$Screen Shot 2019-05-29 a las 2.20.55 PM.png$

Ejercicio$\PageIndex{24}$

Para dibujar la gráfica de la función$f(x) = \sqrt{1−x}$, realice cada uno de los siguientes pasos en secuencia.

Configure un sistema de coordenadas y esboce la gráfica de$y = \sqrt{x}$. Etiquete la gráfica con su ecuación.
Configure un segundo sistema de coordenadas y esboce la gráfica de$y = \sqrt{−x}$. Etiquete la gráfica con su ecuación.
Configure un tercer sistema de coordenadas y esboce la gráfica de$y =\sqrt{−(x−1)}$. Etiquete la gráfica con su ecuación. Esta es la gráfica de$y =\sqrt{1−x}$. Utilice la notación de intervalos para indicar el dominio y el rango de esta función.

En Ejercicios 25 - 28, realizar cada una de las siguientes tareas.

Dibuja la gráfica de la función dada con tu calculadora gráfica. Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Etiquete su gráfica con su ecuación. Utilice la gráfica para determinar el dominio de la función y describir el dominio con notación de intervalos.
Utilizar un enfoque puramente algebraico para determinar el dominio de la función dada. Usa la notación de intervalos para desescribir tu resultado. ¿Está de acuerdo con el resultado gráfico de la parte 1?

Ejercicio$\PageIndex{25}$

$f(x)= \sqrt{2x+7}$

Contestar

Utilizamos una calculadora gráfica para producir la siguiente gráfica de$f(x)= \sqrt{2x+7}$

$Screen Shot 2019-05-29 en 2.25.51 PM.png$

Estimamos que el dominio constará de todos los números reales a la derecha de aproximadamente − 3. 5. Para encontrar una solución algebraica, tenga en cuenta que no se puede tomar la raíz cuadrada de un número negativo. De ahí que la expresión bajo el radical in$f(x)= \sqrt{2x+7}$ debe ser mayor o igual a cero.

$2x + 7 \ge 0$

$2x \ge −7$

$x \ge −\frac{7}{2}$

De ahí que el dominio sea$[−\frac{7}{2}, \infty)$.

Ejercicio$\PageIndex{26}$

$f(x)= \sqrt{7−2x}$

Ejercicio$\PageIndex{27}$

$f(x)= \sqrt{12−4x}$

Contestar

Utilizamos una calculadora gráfica para producir la siguiente gráfica de$f(x)= \sqrt{12−4x}$.

$Screen Shot 2019-05-29 at 2.31.07 PM.png$

Estimamos que el dominio constará de todos los números reales a la derecha de aproximadamente 3. Para encontrar una solución algebraica, tenga en cuenta que no se puede tomar la raíz cuadrada de un número negativo. De ahí que la expresión bajo el radical in$f(x)= \sqrt{12−4x}$ debe ser mayor o igual a cero.

$12−4x \ge 0$

$−4x \ge −12$

$x \le 3$

De ahí que el dominio sea$(−\infty, 3]$.

Ejercicio$\PageIndex{28}$

$f(x)= \sqrt{12+2x}$

En los Ejercicios 29 - 40, encuentra algebraicamente el dominio de la función dada.

Ejercicio$\PageIndex{29}$

$f(x)= \sqrt{2x+9}$

Contestar: La raíz par de un número negativo no se define como un número real. Así, 2x + 9 debe ser mayor o igual a cero. Ya que$2x + 9 \ge 0$ implica que$x \ge −\frac{9}{2}$, el dominio es el intervalo$[−\frac{9}{2},\infty)$.

Ejercicio$\PageIndex{30}$

$f(x)=\sqrt{−3x+3}$

Ejercicio$\PageIndex{31}$

$f(x)=\sqrt{−8x−3}$

Contestar: La raíz par de un número negativo no se define como un número real. Por lo tanto, −8x−3 debe ser mayor o igual a cero. Ya que$−8x−3 \ge 0$ implica que$x \le −\frac{3}{8}$, el dominio es el intervalo$(−\infty, −\frac{3}{8}]$.

Ejercicio$\PageIndex{32}$

$f(x)=\sqrt{−3x+6}$

Ejercicio$\PageIndex{33}$

$f(x)=\sqrt{−6x−8}$

Contestar: La raíz par de un número negativo no se define como un número real. Por lo tanto, −6x−8 debe ser mayor o igual a cero. Ya que$−6x−8 \ge 0$ implica que$x \le −\frac{4}{3}$, el dominio es el intervalo$(−\infty, \frac{4}{3}]$.

Ejercicio$\PageIndex{34}$

$f(x)=\sqrt{8x−6}$

Ejercicio$\PageIndex{35}$

$f(x)=\sqrt{−7x+2}$

Contestar: La raíz par de un número negativo no se define como un número real. Así, −7x+2 debe ser mayor o igual a cero. Ya que$−7x+2 \ge 0$ implica que$x \le \frac{2}{7}$, el dominio es el intervalo$(−\infty, \frac{2}{7}]$.

Ejercicio$\PageIndex{36}$

$f(x)=\sqrt{8x−3}$

Ejercicio$\PageIndex{37}$

$f(x)=\sqrt{6x+3}$

Contestar: La raíz par de un número negativo no se define como un número real. Así, 6x+3 debe ser mayor o igual a cero. Ya que$6x+3 \ge 0$ implica que$x \ge −\frac{1}{2}$, el dominio es el intervalo$[−\frac{1}{2}, \infty)$.

Ejercicio$\PageIndex{38}$

$f(x)=\sqrt{x−5}$

Ejercicio$\PageIndex{39}$

$f(x)=\sqrt{−7x−8}$

Contestar: La raíz par de un número negativo no se define como un número real. Por lo tanto, −7x−8 debe ser mayor o igual a cero. Ya que$−7x−8 \ge 0$ implica que$x \le −\frac{8}{7}$, el dominio es el intervalo$(−\infty, −\frac{8}{7}]$

Ejercicio$\PageIndex{40}$

$f(x)=\sqrt{7x+8}$

Search

Text Color

Text Size

Margin Size

Font Type