4.5E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112366

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Determinar si un triple ordenado es una solución de un sistema de tres ecuaciones lineales con tres variables

En los siguientes ejercicios, determinar si el triple ordenado es una solución al sistema.

1. $\left\{ \begin{array} {l} 2x−6y+z=3 \\ 3x−4y−3z=2 \\ 2x+3y−2z=3 \end{array} \right. $

ⓐ$(3,1,3)$
ⓑ$(4,3,7)$

2. $\left\{ \begin{array} {l} -3x+y+z=-4 \\ -x+2y-2z=1 \\ 2x-y-z=-1 \end{array} \right. $

ⓐ$(−5,−7,4)$
ⓑ$(5,7,4)$

Responder: ⓐ no ⓑ si

3. $\left\{ \begin{array} {l} y−10z=−8 \\ 2x−y=2 \\ x−5z=3 \end{array} \right. $

ⓐ$(7,12,2)$
ⓑ$(2,2,1)$

4. $\left\{ \begin{array} {l} x+3y−z=1 \\ 5y=\frac{2}{3}x \\ −2x−3y+z=−2 \end{array} \right. $

ⓐ$(−6,5,12)$
ⓑ$(5,\frac{4}{3},−3)$

Responder: ⓐ no ⓑ si

Resolver un Sistema de Ecuaciones Lineales con Tres Variables

En los siguientes ejercicios, resolver el sistema de ecuaciones.

5. $\left\{ \begin{array} {l} 5x+2y+z=5 \\ −3x−y+2z=6 \\ 2x+3y−3z=5 \end{array} \right. $

6. $\left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. $

Responder: $(4,5,2)$

7. $\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

8. $\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. $

Responder: $(7,12,−2)$

9. $\left\{ \begin{array} {l} 3x−5y+4z=5 \\ 5x+2y+z=0 \\ 2x+3y−2z=3 \end{array} \right. $

10. $\left\{ \begin{array} {l} 4x−3y+z=7 \\ 2x−5y−4z=3 \\ 3x−2y−2z=−7 \end{array} \right. $

Responder: $(−3,−5,4)$

11. $\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. $

12. $\left\{ \begin{array} {l} 11x+9y+2z=−9 \\ 7x+5y+3z=−7 \\ 4x+3y+z=−3 \end{array} \right. $

Responder: $(2,−3,−2)$

13. $\left\{ \begin{array} {l} \frac{1}{3}x−y−z=1 \\ x+\frac{5}{2}y+z=−2 \\ 2x+2y+\frac{1}{2}z=−4 \end{array} \right. $

14. $\left\{ \begin{array} {l} x+\frac{1}{2}y+\frac{1}{2}z=0 \\ \frac{1}{5}x−\frac{1}{5}y+z=0 \\ \frac{1}{3}x−\frac{1}{3}y+2z=−1 \end{array} \right. $

Responder: $(6,−9,−3)$

15. $\left\{ \begin{array} {l} x+\frac{1}{3}y−2z=−1 \\ \frac{1}{3}x+y+\frac{1}{2}z=0 \\ \frac{1}{2}x+\frac{1}{3}y−\frac{1}{2}z=−1 \end{array} \right. $

16. $\left\{ \begin{array} {l} \frac{1}{3}x−y+\frac{1}{2}z=4 \\ \frac{2}{3}x+\frac{5}{2}y−4z=0 \\ x−\frac{1}{2}y+\frac{3}{2}z=2 \end{array} \right. $

Responder: $(3,−4,−2)$

17. $\left\{ \begin{array} {l} x+2z=0 \\ 4y+3z=−2 \\ 2x−5y=3 \end{array} \right. $

18. $\left\{ \begin{array} {l} 2x+5y=4 \\ 3y−z=\frac{3}{4} \\ x+3z=−3 \end{array} \right. $

Responder: $(−3,2,3)$

19. $\left\{ \begin{array} {l} 2y+3z=−1 \\ 5x+3y=−6 \\ 7x+z=1 \end{array} \right. $

20. $\left\{ \begin{array} {l} 3x−z=−3 \\ 5y+2z=−6 \\ 4x+3y=−8 \end{array} \right. $

Responder: $(−2,0,−3)$

21. $\left\{ \begin{array} {l} 4x−3y+2z=0 \\ −2x+3y−7z=1 \\ 2x−2y+3z=6 \end{array} \right. $

22. $\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. $

Responder: sin solución

23. $\left\{ \begin{array} {l} 2x+3y+z=1 \\ 2x+y+z=9 \\ 3x+4y+2z=20 \end{array} \right. $

24. $\left\{ \begin{array} {l} x+4y+z=−8 \\ 4x−y+3z=9 \\ 2x+7y+z=0 \end{array} \right. $

Responder: $x=\frac{203}{16};\space y=–\frac{25}{16};\space z=–\frac{231}{16};$

25. $\left\{ \begin{array} {l} x+2y+z=4 \\ x+y−2z=3 \\ −2x−3y+z=−7 \end{array} \right. $

26. $\left\{ \begin{array} {l} x+y−2z=3 \\ −2x−3y+z=−7 \\ x+2y+z=4 \end{array} \right. $

Responder: $(x,y,z)$donde$x=5z+2;\space y=−3z+1;\space z$ esta cualquier numero real

27. $\left\{ \begin{array} {l} x+y−3z=−1 \\ y−z=0 \\ −x+2y=1 \end{array} \right. $

28. $\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. $

Responder: $(x,y,z)$donde$x=5z−2;\space y=4z−3;\space z$ esta cualquier numero real

Resolver aplicaciones usando sistemas de ecuaciones lineales con tres variables

En los siguientes ejercicios, resolver el problema dado.

29. La suma de las medidas de los ángulos de un triángulo es 180. La suma de las medidas del segundo y tercer ángulo es el doble de la medida del primer ángulo. El tercer ángulo es doce más que el segundo. Encuentra las medidas de los tres ángulos.

30. La suma de las medidas de los ángulos de un triángulo es 180. La suma de las medidas del segundo y tercer ángulo es tres veces la medida del primer ángulo. El tercer ángulo es quince más que el segundo. Encuentra las medidas de los tres ángulos.

Responder: 42, 50, 58

31. Después de ver una importante producción musical en el teatro, los mecenas pueden comprar recuerdos. Si una familia compra 4 playeras, el video y 1 peluche, su total es de 135 dólares.

Una pareja compra 2 playeras, el video, y 3 peluches para sus sobrinas y gasta 115 dólares. Otra pareja compra 2 playeras, el video, y 1 peluche y su total es de 85 dólares. ¿Cuál es el costo de cada artículo?

32. El grupo de jóvenes de la iglesia está vendiendo bocadillos para recaudar dinero para asistir a su convención. Amy vendió 2 libras de dulces, 3 cajas de galletas y 1 lata de palomitas de maíz por un total de ventas de $65. Brian vendió 4 libras de dulces, 6 cajas de galletas y 3 latas de palomitas de maíz por un total de ventas de $140. Paulina vendió 8 libras de dulces, 8 cajas de galletas y 5 latas de palomitas de maíz para un total de ventas de $250. ¿Cuál es el costo de cada artículo?

Responder: $20, $5, $10

Ejercicios de escritura

33. En sus propias palabras explique los pasos para resolver un sistema de ecuaciones lineales con tres variables por eliminación.

34. ¿Cómo se puede saber cuando un sistema de tres ecuaciones lineales con tres variables no tiene solución? ¿Infinitamente muchas soluciones?

Responder: Las respuestas variarán.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

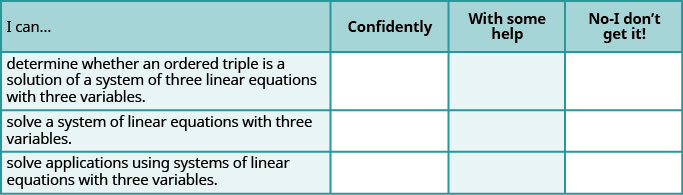
$Esta tabla tiene 4 columnas, 3 filas y una fila de cabecera. La fila de encabezado etiqueta cada columna puedo, con confianza, con algo de ayuda y no, no la consigo. La primera fila contiene las siguientes declaraciones: determinar si un triple ordenado es una solución de un sistema de tres ecuaciones lineales con tres variables, resolver un sistema de ecuaciones lineales con tres variables, resolver aplicaciones usando sistemas de ecuaciones lineales con tres variables. Las columnas restantes están en blanco.$

ⓑ En una escala del 1-10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?