4.5: Resolver sistemas de ecuaciones con tres variables
- Page ID
- 112362
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Al final de esta sección, podrás:
- Determinar si un triple ordenado es una solución de un sistema de tres ecuaciones lineales con tres variables
- Resolver un sistema de ecuaciones lineales con tres variables
- Resolver aplicaciones usando sistemas de ecuaciones lineales con tres variables
Antes de comenzar, toma este cuestionario de preparación.
- Evalúa\(5x−2y+3z\) cuándo\(x=−2, y=−4,\) y\(z=3.\)
si te perdiste este problema, revisa [link]. - Clasificar las ecuaciones como una ecuación condicional, una identidad o una contradicción y luego declarar la solución. \( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
Si te perdiste este problema, revisa [enlace]. - Clasificar las ecuaciones como una ecuación condicional, una identidad o una contradicción y luego declarar la solución. \(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right. \)
Si te perdiste este problema, revisa [enlace].
Determinar si un triple ordenado es una solución de un sistema de tres ecuaciones lineales con tres variables
En esta sección, ampliaremos nuestro trabajo de resolución de un sistema de ecuaciones lineales. Hasta el momento hemos trabajado con sistemas de ecuaciones con dos ecuaciones y dos variables. Ahora trabajaremos con sistemas de tres ecuaciones con tres variables. Pero primero revisemos lo que ya sabemos sobre la resolución de ecuaciones y sistemas que involucran hasta dos variables.
Aprendimos antes que la gráfica de una ecuación lineal,\(ax+by=c\), es una línea. Cada punto de la línea, un par ordenado\((x,y)\), es una solución a la ecuación. Para un sistema de dos ecuaciones con dos variables, graficamos dos líneas. Entonces podemos ver que todos los puntos que son soluciones a cada ecuación forman una línea. Y, al encontrar lo que tienen en común las líneas, encontraremos la solución al sistema.
La mayoría de las ecuaciones lineales en una variable tienen una solución, pero vimos que algunas ecuaciones, llamadas contradicciones, no tienen soluciones y para otras ecuaciones, llamadas identidades, todos los números son soluciones
Sabemos que cuando resolvemos un sistema de dos ecuaciones lineales representadas por una gráfica de dos líneas en un mismo plano, hay tres casos posibles, como se muestra.
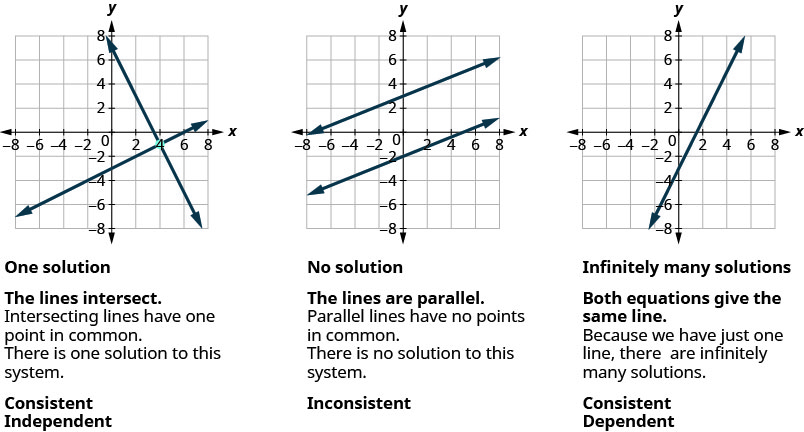
De igual manera, para una ecuación lineal con tres variables ax+by+cz=d, ax+by+cz=d, cada solución a la ecuación es un triple ordenado, (x, y, z) (x, y, z) que hace que la ecuación sea verdadera.
Una ecuación lineal con tres variables, donde a, b, c y d son números reales y a, b y c no son todos 0, es de la forma
\[ ax+by+cz=d\nonumber \]
Toda solución a la ecuación es un triple ordenado,\((x,y,z)\) eso hace que la ecuación sea cierta.
Todos los puntos que son soluciones a una ecuación forman un plano en el espacio tridimensional. Y, al encontrar lo que tienen en común los aviones, encontraremos la solución al sistema.
Cuando resolvemos un sistema de tres ecuaciones lineales representadas por una gráfica de tres planos en el espacio, hay tres casos posibles.
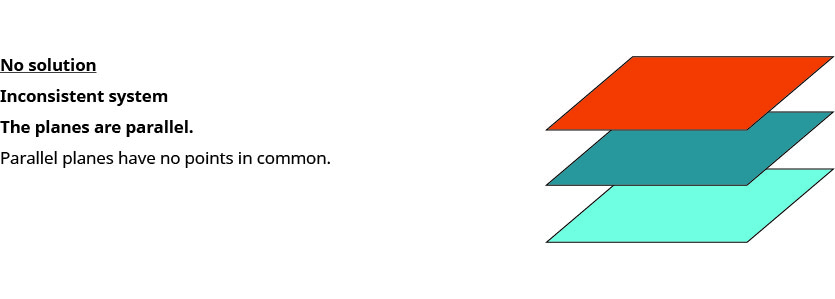
Para resolver un sistema de tres ecuaciones lineales, queremos encontrar los valores de las variables que son soluciones a las tres ecuaciones. En otras palabras, estamos buscando el triple ordenado\((x,y,z)\) que haga verdaderas las tres ecuaciones. A estas se les llama las soluciones del sistema de tres ecuaciones lineales con tres variables.
Las soluciones de un sistema de ecuaciones son los valores de las variables que hacen verdaderas todas las ecuaciones. Una solución está representada por un triple ordenado\((x,y,z)\).
Para determinar si un triple ordenado es una solución a un sistema de tres ecuaciones, sustituimos los valores de las variables en cada ecuación. Si el triple ordenado hace que las tres ecuaciones sean verdaderas, es una solución para el sistema.
Determine si el triple ordenado es una solución para el sistema:\( \left\{ \begin{array} {l} x−y+z=2 \\ 2x−y−z=−6 \\ 2x+2y+z=−3 \end{array} \right. \)
ⓐ\((−2,−1,3)\) ⓑ\((−4,−3,4)\)
- Responder
-
ⓐ
ⓑ
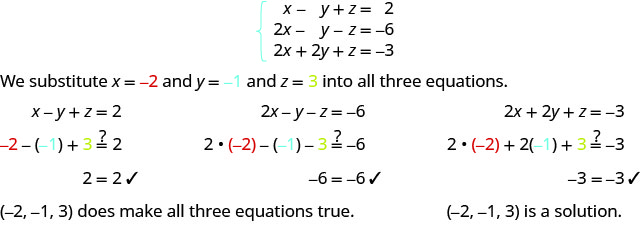
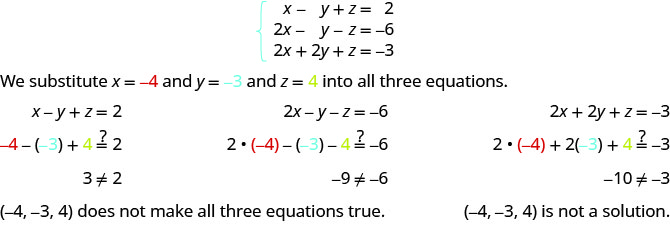
Determine si el triple ordenado es una solución para el sistema:\( \left\{ \begin{array} {l} 3x+y+z=2 \\ x+2y+z=−3 \\ 3x+y+2z=4 \end{array} \right. \)
ⓐ\((1,−3,2)\) ⓑ\((4,−1,−5)\)
- Responder
-
ⓐ si ⓑ no
Determine si el triple ordenado es una solución para el sistema:\( \left\{ \begin{array} {l} x−3y+z=−5 \\ −3x−y−z=1 \\ 2x−2y+3z=1 \end{array} \right. \)
ⓐ\((2,−2,3)\) ⓑ\((−2,2,3)\)
- Responder
-
ⓐ no ⓑ si
Resolver un Sistema de Ecuaciones Lineales con Tres Variables
Para resolver un sistema de ecuaciones lineales con tres variables, básicamente utilizamos las mismas técnicas que usamos con sistemas que tenían dos variables. Comenzamos con dos pares de ecuaciones y en cada par eliminamos la misma variable. Esto nos dará entonces un sistema de ecuaciones con sólo dos variables y entonces ¡ya sabemos cómo resolver ese sistema!
A continuación, utilizamos los valores de las dos variables que acabamos de encontrar para volver a la ecuación original y encontrar la tercera variable. Escribimos nuestra respuesta como un triple ordenado y luego verificamos nuestros resultados.
Resuelve el sistema por eliminación:\( \left\{ \begin{array} {l} x−2y+z=3 \\ 2x+y+z=4 \\ 3x+4y+3z=−1 \end{array} \right. \)
- Responder
-
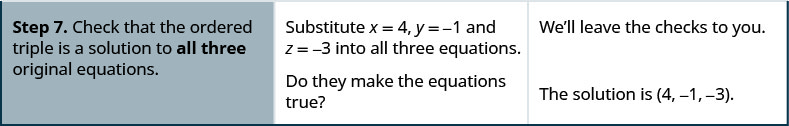
Resuelve el sistema por eliminación:\( \left\{ \begin{array} {l} 3x+y−z=2 \\ 2x−3y−2z=1 \\ 4x−y−3z=0 \end{array} \right.\)
- Responder
-
\((2,−1,3)\)
Resuelve el sistema por eliminación:\( \left\{ \begin{array} {l} 4x+y+z=−1 \\ −2x−2y+z=2 \\ 2x+3y−z=1 \end{array} \right. \)
- Responder
-
\((−2,3,4)\)
Aquí se resumen los pasos.
- Escribir las ecuaciones en forma estándar
- Si alguno de los coeficientes son fracciones, límpielos.
- Elimina la misma variable de dos ecuaciones.
- Decide qué variable vas a eliminar.
- Trabajar con un par de ecuaciones para eliminar la variable elegida.
- Multiplique una o ambas ecuaciones para que los coeficientes de esa variable sean opuestos.
- Sumar las ecuaciones resultantes del paso 2 para eliminar una variable
- Repita el Paso 2 usando otras dos ecuaciones y elimine la misma variable que en el Paso 2.
- Las dos nuevas ecuaciones forman un sistema de dos ecuaciones con dos variables. Resuelve este sistema.
- Utilice los valores de las dos variables que se encuentran en el Paso 4 para encontrar la tercera variable.
- Escribe la solución como un triple ordenado.
- Verifique que el triple ordenado sea una solución a las tres ecuaciones originales.
Resolver:\( \left\{ \begin{array} {l} 3x−4z=0 \\ 3y+2z=−3 \\ 2x+3y=−5 \end{array} \right. \)
- Responder
-
\[ \left\{ \begin{array} {ll} 3x−4z=0 &(1) \\ 3y+2z=−3 &(2) \\ 2x+3y=−5 &(3) \end{array} \right. \nonumber \]
Podemos eliminar\(z\) de las ecuaciones (1) y (2) multiplicando la ecuación (2) por 2 y luego sumando las ecuaciones resultantes.
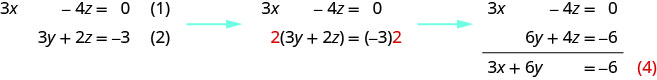
Observe que las ecuaciones (3) y (4) ambas tienen las variables\(x\) y\(y\). Vamos a resolver este nuevo sistema para\(x\) y\(y\).
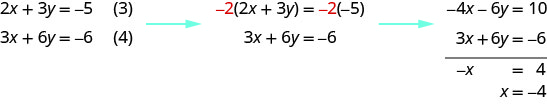
Para resolver por y, sustituimos\(x=−4\) en la ecuación (3).
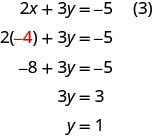
Ahora tenemos\(x=−4\) y\(y=1\). Tenemos que resolver para z. Podemos sustituir\(x=−4\) en la ecuación (1) para encontrar z.
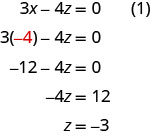
Escribimos la solución como un triple ordenado. \((−4,1,−3)\)
Comprobamos que la solución hace que las tres ecuaciones sean verdaderas.
\(\begin{array} {lll} {3x-4z=0 \space (1)} &{3y+2z=−3 \space (2)} &{2x+3y=−5 \space (3)} \\ {3(−4)−4(−3)\overset{?}{=} 0} &{3(1)+2(−3)\overset{?}{=} −3} &{2(−4)+3(1)\overset{?}{=} −5} \\ {0=0 \checkmark} &{−3=−3 \checkmark} &{−5=−5 \checkmark} \\ {} &{} &{\text{The solution is }(−4,1,−3)} \end{array}\)
Resolver:\( \left\{ \begin{array} {l} 3x−4z=−1 \\ 2y+3z=2 \\ 2x+3y=6 \end{array} \right. \)
- Responder
-
\((−3,4,−2)\)
Resolver:\( \left\{ \begin{array} {l} 4x−3z=−5 \\ 3y+2z=7 \\ 3x+4y=6 \end{array} \right. \)
- Responder
-
\((−2,3,−1)\)
Cuando resolvemos un sistema y terminamos sin variables y una declaración falsa, sabemos que no hay soluciones y que el sistema es inconsistente. El siguiente ejemplo muestra un sistema de ecuaciones que es inconsistente.
Resolver el sistema de ecuaciones:\( \left\{ \begin{array} {l} x+2y−3z=−1 \\ x−3y+z=1 \\ 2x−y−2z=2 \end{array} \right. \)
- Responder
-
\[\left\{ \begin{array} {ll} x+2y−3z=−1 &(1) \\ x−3y+z=1 &(2) \\ 2x−y−2z=2 &(3) \end{array} \right.\nonumber \]
Utilice las ecuaciones (1) y (2) para eliminar z.
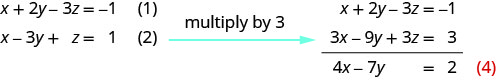
Use (2) y (3) para eliminar de\(z\) nuevo.
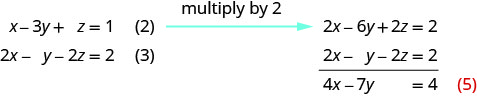
Utilizar (4) y (5) para eliminar una variable.
No hay solución.
Nos quedamos con una declaración falsa y esto nos dice que el sistema es inconsistente y no tiene solución.
Resolver el sistema de ecuaciones:\( \left\{ \begin{array} {l} x+2y+6z=5 \\ −x+y−2z=3 \\ x−4y−2z=1 \end{array} \right. \)
- Responder
-
sin solución
Resolver el sistema de ecuaciones:\( \left\{ \begin{array} {l} 2x−2y+3z=6 \\ 4x−3y+2z=0 \\ −2x+3y−7z=1 \end{array} \right. \)
- Responder
-
sin solución
Cuando resolvemos un sistema y terminamos sin variables sino con una afirmación verdadera, sabemos que hay infinitamente muchas soluciones. El sistema es consistente con ecuaciones dependientes. Nuestra solución mostrará cómo dos de las variables dependen de la tercera.
Resolver el sistema de ecuaciones:\( \left\{ \begin{array} {l} x+2y−z=1 \\ 2x+7y+4z=11 \\ x+3y+z=4 \end{array} \right. \)
- Responder
-
\[\left\{ \begin{array} {ll} x+2y−z=1 &(1) \\ 2x+7y+4z=11 &(2) \\ x+3y+z=4 &(3) \end{array} \right.\nonumber \]
Utilice las ecuaciones (1) y (3) para eliminar x.
Usa las ecuaciones (1) y (2) para eliminar x nuevamente.
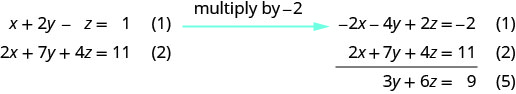
Utilice las ecuaciones (4) y (5) para eliminar\(y\).
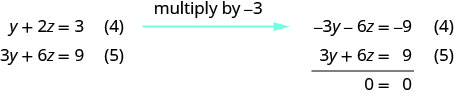
Hay infinitamente muchas soluciones. Resolver la ecuación (4) para y. Representar la solución mostrando cómo x e y son dependientes de z.
\( \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} \)Utilice la ecuación (1) para resolver para x. \( x+2y−z=1\) Sustituto\(y=−2z+3\). \( \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} \) La verdadera afirmación nos\(0=0\) dice que se trata de un sistema dependiente que tiene infinitamente muchas soluciones. Las soluciones son de la forma (x, y, z) (x, y, z) donde\(x=5z−5;\space y=−2z+3\) y z es cualquier número real.
Resolver el sistema por ecuaciones:\( \left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)
- Responder
-
infinitamente muchas soluciones\((x,3,z)\) donde\(x=z−3;\space y=3;\space z\) está cualquier número real
Resolver el sistema por ecuaciones:\( \left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)
- Responder
-
infinitamente muchas soluciones\((x,y,z)\) donde\(x=5z−2;\space y=4z−3;\space z\) está cualquier número real
Resolver Aplicaciones usando Sistemas de Ecuaciones Lineales con Tres Variables
Las aplicaciones que son modeladas por un sistema de ecuaciones se pueden resolver utilizando las mismas técnicas que usamos para resolver los sistemas. Muchas de las aplicaciones son solo extensiones a tres variables de los tipos que hemos resuelto anteriormente.
El departamento de teatro de community college vendió tres tipos de boletos para su última producción teatral. Los boletos para adultos se vendieron por $15, los boletos de estudiante por $10 y los boletos para niños por $8. El departamento de teatro estaba encantado de haber vendido 250 boletos y traído $2,825 en una noche. El número de boletos de estudiante vendidos es el doble del número de boletos de adultos vendidos. ¿Cuántos de cada tipo vendió el departamento?
- Responder
-
Usaremos un gráfico para organizar la información.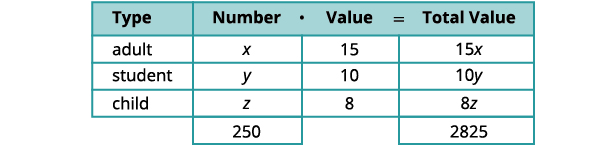 
Número de alumnos es el doble número de adultos. Reescribir la ecuación en forma estándar. \(\begin{aligned} y &= 2x \\ 2x−y &= 0 \end{aligned} \) 
Utilice las ecuaciones (1) y (2) para eliminar z.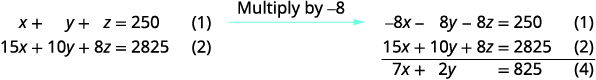 
Use (3) y (4) para eliminar\(y\).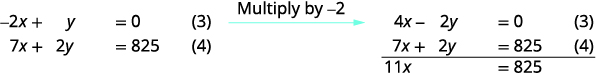 
Resolver para x. \(x=75 \)boletos para adultos Utilice la ecuación (3) para encontrar y. \(−2x+y=0\) Sustituto\(x=75\). \(\begin{aligned} −2(75)+y &= 0 \\ −150+y &= 0 \\ y &= 150\text{ student tickets}\end{aligned} \) Usa la ecuación (1) para encontrar z. \(x+y+z=250\) Sustituto en los valores
\(x=75, \space y=150.\)
\(\begin{aligned} 75+150+z &= 250 \\ 225+z &= 250 \\ z &= 25\text{ child tickets} \end{aligned} \)Escribe la solución. El departamento de teatro vendió 75 boletos para adultos,
150 boletos para estudiantes y 25 boletos para niños.
El departamento de bellas artes de community college vendió tres tipos de boletos para su última presentación de baile. Los boletos para adultos se vendieron por $20, los boletos de estudiante por 12 dólares y los boletos para niños por 10.El departamento de bellas artes se emocionó de haber vendido 350 boletos y traído $4,650 en una noche. El número de boletos infantiles vendidos es el mismo que el número de boletos de adulto vendidos. ¿Cuántos de cada tipo vendió el departamento?
- Responder
-
El departamento de bellas artes vendió 75 boletos para adultos, 200 boletos para estudiantes y 75 boletos para niños.
El equipo de futbol community college vendió tres tipos de boletos para su último juego. Los boletos para adultos se vendieron por $10, los boletos de estudiante por $8 y los boletos infantiles por $5. El equipo de futbol estaba encantado de haber vendido 600 boletos y traído $4,900 para un juego. El número de boletos para adultos es el doble del número de boletos infantiles. ¿Cuántos de cada tipo vendió el equipo de futbol?
- Responder
-
El equipo de futbol vendió 200 boletos para adultos, 300 boletos para estudiantes y 100 boletos para niños.
Acceda a este recurso en línea para obtener instrucción adicional y práctica con la resolución de un sistema lineal en tres variables sin soluciones o infinitas.
- Resolver un sistema lineal en tres variables sin soluciones o infinitas
- 3 Aplicación Variable
Conceptos clave
- Ecuación lineal en tres variables: Una ecuación lineal con tres variables, donde a, b, c y d son números reales y a, b y c no son todos 0, es de la forma
\[ax+by+cz=d\nonumber \]
Toda solución a la ecuación es un triple ordenado,\((x,y,z)\) eso hace que la ecuación sea cierta. - Cómo resolver un sistema de ecuaciones lineales con tres variables.
- Escribe las ecuaciones en forma estándar
Si alguno de los coeficientes son fracciones, límpialas. - Elimina la misma variable de dos ecuaciones.
Decide qué variable vas a eliminar.
Trabajar con un par de ecuaciones para eliminar la variable elegida.
Multiplica una o ambas ecuaciones para que los coeficientes de esa variable sean opuestos.
Sumar las ecuaciones resultantes del paso 2 para eliminar una variable - Repita el Paso 2 usando otras dos ecuaciones y elimine la misma variable que en el Paso 2.
- Las dos nuevas ecuaciones forman un sistema de dos ecuaciones con dos variables. Resuelve este sistema.
- Utilice los valores de las dos variables que se encuentran en el Paso 4 para encontrar la tercera variable.
- Escribe la solución como un triple ordenado.
- Verifique que el triple ordenado sea una solución a las tres ecuaciones originales.
- Escribe las ecuaciones en forma estándar
Glosario
- soluciones de un sistema de ecuaciones lineales con tres variables
- Las soluciones de un sistema de ecuaciones son los valores de las variables que hacen verdaderas todas las ecuaciones; una solución está representada por un triple ordenado (x, y, z).