6.3E: Ejercicios
- Page ID
- 112413
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La práctica hace la perfección
Trinomios factoriales de la Forma\(x^2+bx+c\)
En los siguientes ejercicios, factorizar cada trinomio de la forma\(x^2+bx+c\).
1. \(p^2+11p+30\)
- Contestar
-
\((p+5)(p+6)\)
2. \(w^2+10w+21\)
3. \(n^2+19n+48\)
- Contestar
-
\((n+3)(n+16)\)
4. \(b^2+14b+48\)
5. \(a^2+25a+100\)
- Contestar
-
\((a+5)(a+20)\)
6. \(u^2+101u+100\)
7. \(x^2−8x+12\)
- Contestar
-
\((x−2)(x−6)\)
8. \(q^2−13q+36\)
9. \(y^2−18y+45\)
- Contestar
-
\((y−3)(y−15)\)
10. \(m^2−13m+30\)
11. \(x^2−8x+7\)
- Contestar
-
\((x−1)(x−7)\)
12. \(y^2−5y+6\)
13. \(5p−6+p^2\)
- Contestar
-
\((p−1)(p+6)\)
14. \(6n−7+n^2\)
15. \(8−6x+x^2\)
- Contestar
-
\((x−4)(x−2)\)
16. \(7x+x^2+6\)
17. \(x^2−12−11x\)
- Contestar
-
\((x−12)(x+1)\)
18. \(−11−10x+x^2\)
En los siguientes ejercicios, factorizar cada trinomio de la forma\(x^2+bxy+cy^2\).
19. \(x^2−2xy−80y^2\)
- Contestar
-
\((x+8y)(x−10y)\)
20. \(p^2−8pq−65q^2\)
21. \(m^2−64mn−65n^2\)
- Contestar
-
\((m+n)(m−65n)\)
22. \(p^2−2pq−35q^2\)
23. \(a^2+5ab−24b^2\)
- Responder
-
\((a+8b)(a−3b)\)
24. \(r^2+3rs−28s^2\)
25. \(x^2−3xy−14y^2\)
- Responder
-
Prime
26. \(u^2−8uv−24v^2\)
27. \(m^2−5mn+30n^2\)
- Responder
-
Prime
28. \(c^2−7cd+18d^2\)
Trinomios factoriales de la forma\(ax^2+bx+c\) mediante ensayo y error
En los siguientes ejercicios, factorizar completamente usando ensayo y error.
29. \(p^3−8p^2−20p\)
- Responder
-
\(p(p−10)(p+2)\)
30. \(q^3−5q^2−24q\)
31. \(3m^3−21m^2+30m\)
- Responder
-
\(3m(m−5)(m−2)\)
32. \(11n^3−55n^2+44n\)
33. \(5x^4+10x^3−75x^2\)
- Responder
-
\(5x^2(x−3)(x+5)\)
34. \(6y^4+12y^3−48y^2\)
35. \(2t^2+7t+5\)
- Responder
-
\((2t+5)(t+1)\)
36. \(5y^2+16y+11\)
37. \(11x^2+34x+3\)
- Responder
-
\((11x+1)(x+3)\)
38. \(7b^2+50b+7\)
39. \(4w^2−5w+1\)
- Responder
-
\((4w−1)(w−1)\)
40. \(5x^2−17x+6\)
41. \(4q^2−7q−2\)
- Responder
-
\((4q+1)(q−2)\)
42. \(10y^2−53y−111\)
43. \(6p^2−19pq+10q^2\)
- Responder
-
\((2p−5q)(3p−2q)\)
44. \(21m^2−29mn+10n^2\)
45. \(4a^2+17ab−15b^2\)
- Responder
-
\((4a−3b)(a+5b)\)
46. \(6u^2+5uv−14v^2\)
47. \(−16x^2−32x−16\)
- Responder
-
\(−16(x+1)(x+1)\)
48. \(−81a^2+153a+18\)
49. \(−30q^3−140q^2−80q\)
- Responder
-
\( - 10q(3q+2)(q+4)\)
50. \(−5y^3−30y^2+35y\)
Trinomios factoriales de la Forma\(ax^2+bx+c\) usando el Método 'ac'
En los siguientes ejercicios, factorizar utilizando el método 'ac'.
51. \(5n^2+21n+4\)
- Responder
-
\((5n+1)(n+4)\)
52. \(8w^2+25w+3\)
53. \(4k^2−16k+15\)
- Responder
-
\((2k−3)(2k−5)\)
54. \(5s^2−9s+4\)
55. \(6y^2+y−15\)
- Responder
-
\((3y+5)(2y−3)\)
56. \(6p^2+p−22\)
57. \(2n^2−27n−45\)
- Responder
-
\((2n+3)(n−15)\)
58. \(12z^2−41z−11\)
59. \(60y^2+290y−50\)
- Responder
-
\(10(6y−1)(y+5)\)
60. \(6u^2−46u−16\)
61. \(48z^3−102z^2−45z\)
- Responder
-
\(3z(8z+3)(2z−5)\)
62. \(90n^3+42n^2−216n\)
63. \(16s^2+40s+24\)
- Responder
-
\(8(2s+3)(s+1)\)
64. \(24p^2+160p+96\)
65. \(48y^2+12y−36\)
- Responder
-
\(12(4y−3)(y+1)\)
66. \(30x^2+105x−60\)
Factor mediante sustitución
En los siguientes ejercicios, factorizar el uso de la sustitución.
67. \(x^4−x^2−12\)
- Responder
-
\((x^2+3)(x^2−4)\)
68. \(x^4+2x^2−8\)
69. \(x^4−3x^2−28\)
- Responder
-
\((x^2−7)(x^2+4)\)
70. \(x^4−13x^2−30\)
71. \((x−3)^2−5(x−3)−36\)
- Responder
-
\((x−12)(x+1)\)
72. \((x−2)^2−3(x−2)−54\)
73. \((3y−2)^2−(3y−2)−2\)
- Responder
-
\((3y−4)(3y−1)\)
74. \((5y−1)^2−3(5y−1)−18\)
Práctica Mixta
En los siguientes ejercicios, factorizar cada expresión utilizando cualquier método.
75. \(u^2−12u+36\)
- Responder
-
\((u−6)(u−6)\)
76. \(x^2−14x−32\)
77. \(r^2−20rs+64s^2\)
- Responder
-
\((r−4s)(r−16s)\)
78. \(q^2−29qr−96r^2\)
79. \(12y^2−29y+14\)
- Responder
-
\((4y−7)(3y−2)\)
80. \(12x^2+36y−24z\)
81. \(6n^2+5n−4\)
- Responder
-
\((2n−1)(3n+4)\)
82. \(3q^2+6q+2\)
83. \(13z^2+39z−26\)
- Responder
-
\(13(z^2+3z−2)\)
84. \(5r^2+25r+30\)
85. \(3p^2+21p\)
- Responder
-
\(3p(p+7)\)
86. \(7x^2−21x\)
87. \(6r^2+30r+36\)
- Responder
-
\(6(r+2)(r+3)\)
88. \(18m^2+15m+3\)
89. \(24n^2+20n+4\)
- Responder
-
\(4(2n+1)(3n+1)\)
90. \(4a^2+5a+2\)
91. \(x^4−4x^2−12\)
- Responder
-
\((x^2+2)(x^2−6)\)
92. \(x^4−7x^2−8\)
93. \((x+3)^2−9(x+3)−36\)
- Responder
-
\((x−9)(x+6)\)
94. \((x+2)^2−25(x+2)−54\)
Ejercicios de escritura
95. Muchos trinomios del\(x^2+bx+c\) factor de forma en el producto de dos binomios\((x+m)(x+n)\). Explica cómo encuentras los valores de\(m\) y\(n\).
- Responder
-
Las respuestas variarán.
96. Tommy factorizado\(x^2−x−20\) como\((x+5)(x−4)\). Sara lo factorizó como\((x+4)(x−5)\). Ernesto lo factorizó como\((x−5)(x−4)\). ¿Quién está en lo correcto? Explique por qué los otros dos están equivocados.
97. Enumere, en orden, todos los pasos que realice al usar el método “\(ac\)” para factorizar un trinomio de la forma\(ax^2+bx+c\).
- Responder
-
Las respuestas variarán.
98. ¿Cómo es el método “\(ac\)” similar al método “undo FOIL”? ¿En qué se diferencia?
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
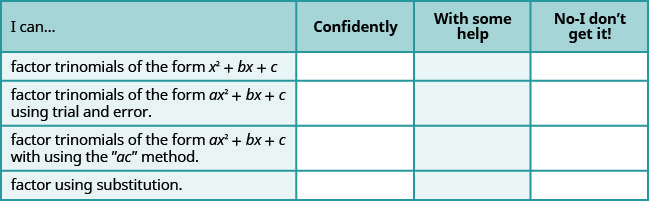
b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?