6.5: Estrategia General para Factorizar Expresiones Polinómicas

Objetivos de aprendizaje

Al final de esta sección, podrás:

• Reconocer y utilizar el método apropiado para factorizar un polinomio completamente

Reconocer y Utilizar el Método Apropiado para Factorizar un Polinomio Completamente

Ahora te has familiarizado con todos los métodos de factorización que necesitarás en este curso. La siguiente tabla resume todos los métodos de factorización que hemos cubierto, y describe una estrategia que debe usar al factorizar polinomios.

ESTRATEGIA GENERAL DE FACTORIZACIÓN DE POLINOMIOS

UTILIZAR UNA ESTRATEGIA GENERAL PARA FACTORAR POLINOMIOS

1. ¿Hay un factor común más grande?
   Factorializarlo.
2. ¿Es el polinomio un binomio, trinomio, o hay más de tres términos?
   Si se trata de un binomio:
   • ¿Es una suma?
     ¿De plazas? Las sumas de cuadrados no facetúan.
     ¿De cubos? Usa el patrón de suma de cubos.
   • ¿Es una diferencia?
     ¿De plazas? Factor como el producto de los conjugados.
     ¿De cubos? Usa la diferencia de patrón de cubos.
   Si se trata de un trinomio:
   • ¿Es de la forma\(x^2+bx+c\)? Deshacer FOIL.
   • ¿Es de la forma\(ax^2+bx+c\)?
     Si a y c son cuadrados, verifique si se ajusta al patrón cuadrado trinomial.
     Utilice el método de prueba y error o “\(ac\)”.
   Si tiene más de tres términos:
   • Utilice el método de agrupación.
3. Cheque.
   ¿Se factoriza por completo?
   ¿Los factores se multiplican de nuevo al polinomio original?

Recuerda, un polinomio está completamente factorizado si, aparte de los monomios, ¡sus factores son primos!

Ejemplo\(\PageIndex{1}\)

Factor completamente:\(7x^3−21x^2−70x\).

Solución

\(\begin{array} {ll} {7x^3−21x^2−70x} & \\ \text{Is there a GCF? Yes, }7x. & \\ \text{Factor out the GCF.} &7x(x^2−3x−10) \\ \text{In the parentheses, is it a binomial, trinomial,} & \\ \text{or are there more terms?} & \\ \text{Trinomial with leading coefficient 1.} & \\ \text{“Undo” FOIL.} &7x(x\hspace{8mm})(x\hspace{8mm}) \\ &7x(x+2)(x−5) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Neither binomial can be factored.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ & \\ & \\ \hspace{15mm}7x(x+2)(x−5) & \\ \hspace{10mm}7x(x^2−5x+2x−10) & \\ \hspace{15mm}7x(x^2−3x−10) & \\ \hspace{13mm}7x^3−21x^2−70x\checkmark & \end{array} \)

Pruébalo\(\PageIndex{1}\)

Factor completamente:\(8y^3+16y^2−24y\).

Contestar

\(8y(y−1)(y+3)\)

Pruébalo\(\PageIndex{2}\)

Factor completamente:\(5y^3−15y^2−270y\).

Contestar

\(5y(y−9)(y+6)\)

¡Ten cuidado cuando te pidan factorizar un binomio ya que hay varias opciones!

Ejemplo\(\PageIndex{2}\)

Factor completamente:\(24y^2−150\)

Solución

\(\begin{array} {ll} &24y^2−150 \\ \text{Is there a GCF? Yes, }6. & \\ \text{Factor out the GCF.} &6(4y^2−25) \\ \text{In the parentheses, is it a binomial, trinomial} & \\ \text{or are there more than three terms? Binomial.} & \\ \text{Is it a sum? No.} & \\ \text{Is it a difference? Of squares or cubes? Yes, squares.} &6((2y)^2−(5)^2) \\ \text{Write as a product of conjugates.} &6(2y−5)(2y+5) \\ & \\ & \\ \hspace{5mm}\text{Is the expression factored completely?} & \\ \hspace{5mm}\text{Neither binomial can be factored.} & \\ \text{Check:} & \\ & \\ & \\ \hspace{5mm}\text{Multiply.} & \\ & \\ \hspace{15mm}6(2y−5)(2y+5) & \\ & \\ \hspace{18mm}6(4y^2−25) & \\ \hspace{18mm}24y^2−150\checkmark \end{array}\)

Pruébalo\(\PageIndex{3}\)

Factor completamente:\(16x^3−36x\).

Contestar

\(4x(2x−3)(2x+3)\)

Pruébalo\(\PageIndex{4}\)

Factor completamente:\(27y^2−48\).

Contestar

\(3(3y−4)(3y+4)\)

El siguiente ejemplo se puede factorizar usando varios métodos. Reconocer el patrón de cuadrados trinomiales hará que tu trabajo sea más fácil.

Ejemplo\(\PageIndex{3}\)

Factor completamente:\(4a^2−12ab+9b^2\).

Solución

\(\begin{array} {ll} &4a^2−12ab+9b^2 \\ \text{Is there a GCF? No.} & \\ \text{Is it a binomial, trinomial, or are there more terms?} & \\ \text{Trinomial with }a\neq 1.\text{ But the first term is a perfect square.} \\ \text{Is the last term a perfect square? Yes.} &(2a)^2−12ab+(3b)^2 \\ \text{Does it fit the pattern, }a^2−2ab+b^2?\text{ Yes.} &(2a)^2 −12ab+ (3b)^2 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(2a)(3b)}{\,}^{\swarrow}\\ \text{Write it as a square.} &(2a−3b)^2 \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \quad\text{The binomial cannot be factored.} & \\ \text{Check your answer.} \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{30mm}(2a−3b)^2 \\ \hspace{20mm} (2a)^2−2·2a·3b+(3b)^2 \\ \hspace{24mm}4a^2−12ab+9b^2\checkmark & \end{array} \)

Pruébalo\(\PageIndex{5}\)

Factor completamente:\(4x^2+20xy+25y^2\).

Contestar

\((2x+5y)^2\)

Pruébalo\(\PageIndex{6}\)

Factor completamente:\(9x^2−24xy+16y^2\).

Contestar

\((3x−4y)^2\)

Recuerda, las sumas de cuadrados no factorizan, ¡pero las sumas de cubos sí!

Ejemplo\(\PageIndex{4}\)

Facturar completamente\(12x^3y^2+75xy^2\).

Solución

\(\begin{array} {ll} &12x^3y^2+75xy^2 \\ \text{Is there a GCF? Yes, }3xy^2. & \\ \text{Factor out the GCF.} &3xy^2(4x^2+25) \\ \text{In the parentheses, is it a binomial, trinomial, or are} & \\ \text{there more than three terms? Binomial.} & \\ & \\ \text{Is it a sum? Of squares? Yes.} &\text{Sums of squares are prime.} \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \text{Check:} & \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{15mm}3xy^2(4x^2+25) & \\ \hspace{14mm}12x^3y^2+75xy^2\checkmark \end{array} \)

Pruébalo\(\PageIndex{7}\)

Factor completamente:\(50x^3y+72xy\).

Contestar

\(2xy(25x^2+36)\)

Pruébalo\(\PageIndex{8}\)

Factor completamente:\(27xy^3+48xy\).

Contestar

\(3xy(9y^2+16)\)

Al usar el patrón de suma o diferencia de cubos, tener cuidado con los signos.

Ejemplo\(\PageIndex{5}\)

Factor completamente:\(24x^3+81y^3\).

Solución

¿Existe un GCF? Sí, 3.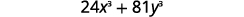
Factorial hacia fuera.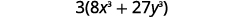
Entre paréntesis, ¿es un binomio, trinomio, de hay más de tres términos? Binomial.
¿Es una suma o diferencia? Suma.
¿De cuadrados o cubos? Suma de cubos.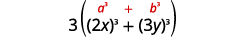
Escríbelo usando el patrón de suma de cubos.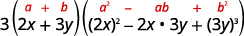
¿Se factoriza completamente la expresión? Sí.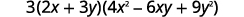
Verificar multiplicando.

Pruébalo\(\PageIndex{9}\)

Factor completamente:\(250m^3+432n^3\).

Contestar

\(2(5m+6n)(25m^2−30mn+36n^2)\)

Pruébalo\(\PageIndex{10}\)

Factor completamente:\(2p^3+54q^3\).

Contestar

\(2(p+3q)(p^2−3pq+9q^2)\)

Ejemplo\(\PageIndex{6}\)

Factor completamente:\(3x^5y−48xy\).

Solución

\(\begin{array} {ll} &3x^5y−48xy \\ \text{Is there a GCF? Factor out }3xy &3xy(x^4−16) \\ \begin{array} {l} \text{Is the binomial a sum or difference? Of squares or cubes?} \\ \text{Write it as a difference of squares.} \end{array} &3xy\left((x^2)^2−(4)2\right) \\ \text{Factor it as a product of conjugates} &3xy(x^2−4)(x^2+4) \\ \text{The first binomial is again a difference of squares.} &3xy\left((x)^2−(2)^2\right)(x^2+4) \\ \text{Factor it as a product of conjugates.} &3xy(x−2)(x+2)(x^2+4) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ 3xy(x−2)(x+2)(x^2+4) & \\ 3xy(x^2−4)(x^2+4) & \\ 3xy(x^4−16) & \\ 3x^5y−48xy\checkmark & \end{array}\)

Pruébalo\(\PageIndex{11}\)

Factor completamente:\(4a^5b−64ab\).

Contestar

\(4ab(a^2+4)(a−2)(a+2)\)

Pruébalo\(\PageIndex{12}\)

Factor completamente:\(7xy^5−7xy\).

Contestar

\(7xy(y^2+1)(y−1)(y+1)\)

Ejemplo\(\PageIndex{7}\)

Factor completamente:\(4x^2+8bx−4ax−8ab\).

Solución

\(\begin{array} {ll} &4x^2+8bx−4ax−8ab \\ \text{Is there a GCF? Factor out the GCF, }4. &4(x^2+2bx−ax−2ab) \\ \text{There are four terms. Use grouping.} &4[x(x+2b)−a(x+2b)]4(x+2b)(x−a) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4(x+2b)(x−a) & \\ \hspace{20mm} 4(x^2−ax+2bx−2ab) & \\ \hspace{20mm}4x^2+8bx−4ax−8ab\checkmark \end{array}\)

Pruébalo\(\PageIndex{13}\)

Factor completamente:\(6x^2−12xc+6bx−12bc\).

Contestar

\(6(x+b)(x−2c)\)

Pruébalo\(\PageIndex{14}\)

Factor completamente:\(16x^2+24xy−4x−6y\).

Contestar

\(2(4x−1)(2x+3y)\)

Sacar el GCF completo en el primer paso siempre hará que tu trabajo sea más fácil.

Ejemplo\(\PageIndex{8}\)

Factor completamente:\(40x^2y+44xy−24y\).

Solución

\(\begin{array} {ll} &40x^2y+44xy−24y \\ \text{Is there a GCF? Factor out the GCF, }4y. &4y(10x^2+11x−6) \\ \text{Factor the trinomial with }a\neq 1. &4y(10x^2+11x−6) \\ &4y(5x−2)(2x+3) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4y(5x−2)(2x+3) & \\ \hspace{24mm}4y(10x^2+11x−6) & \\ \hspace{22mm}40x^2y+44xy−24y\checkmark \end{array}\)

Pruébalo\(\PageIndex{15}\)

Factor completamente:\(4p^2q−16pq+12q\).

Contestar

\(4q(p−3)(p−1)\)

Pruébalo\(\PageIndex{16}\)

Factor completamente:\(6pq^2−9pq−6p\).

Contestar

\(3p(2q+1)(q−2)\)

Cuando hemos factorizado un polinomio con cuatro términos, la mayoría de las veces lo separamos en dos grupos de dos términos. Recuerda que también podemos separarlo en un trinomio y luego en un término.

Ejemplo\(\PageIndex{9}\)

Factor completamente:\(9x^2−12xy+4y^2−49\).

Solución

\(\begin{array} {ll} &9x^2−12xy+4y^2−49 \\ \text{Is there a GCF? No.} & \\ \begin{array} {l} \text{With more than 3 terms, use grouping. Last 2 terms} \\ \text{have no GCF. Try grouping first 3 terms.} \end{array} &9x^2−12xy+4y^2−49 \\ \begin{array} {l} \text{Factor the trinomial with }a\neq 1. \text{ But the first term is a} \\ \text{perfect square.} \end{array} & \\ \text{Is the last term of the trinomial a perfect square? Yes.} &(3x)^2−12xy+(2y)^2−49 \\ \text{Does the trinomial fit the pattern, }a^2−2ab+b^2? \text{ Yes.} &(3x)^2 −12xy+ (2y)^2−49 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(3x)(2y))}{\,}^{\swarrow} \\ \text{Write the trinomial as a square.} &(3x−2y)^2−49 \\ \begin{array} {ll} \text{Is this binomial a sum or difference? Of squares or} \\ \text{cubes? Write it as a difference of squares.} \end{array} &(3x−2y)^2−72 \\ \text{Write it as a product of conjugates.} &((3x−2y)−7)((3x−2y)+7) \\ &(3x−2y−7)(3x−2y+7) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{23mm}(3x−2y−7)(3x−2y+7) & \\ \hspace{10mm}9x^2−6xy−21x−6xy+4y^2+14y+21x−14y−49 \qquad & \\ \hspace{25mm}9x^2−12xy+4y^2−49\checkmark & \end{array}\)

Pruébalo\(\PageIndex{17}\)

Factor completamente:\(4x^2−12xy+9y^2−25\).

Contestar

\((2x−3y−5)(2x−3y+5)\)

Pruébalo\(\PageIndex{18}\)

Factor completamente:\(16x^2−24xy+9y^2−64\).

Contestar

\((4x−3y−8)(4x−3y+8)\)

Conceptos clave

• Cómo utilizar una estrategia general para factorizar polinomios.
  1. ¿Hay un factor común más grande?
     Factorializarlo.
  2. ¿Es el polinomio un binomio, trinomio, o hay más de tres términos?
     Si es un binomio:
     ¿Es una suma?
     ¿De plazas? Las sumas de cuadrados no facetúan.
     ¿De cubos? Usa el patrón de suma de cubos.
     ¿Es una diferencia?
     ¿De plazas? Factor como el producto de los conjugados.
     ¿De cubos? Usa la diferencia de patrón de cubos.
     Si es trinomio:
     ¿Es de la forma\(x^2+bx+c\)? Deshacer FOIL.
     ¿Es de la forma\(ax^2+bx+c\)?
     Si a y c son cuadrados, verifique si se ajusta al patrón cuadrado trinomial.
     Utilice el método de prueba y error o “\(ac\)”.
     Si tiene más de tres términos:
     Usa el método de agrupación.
  3. Cheque.
     ¿Se factoriza por completo?
     ¿Los factores se multiplican de nuevo al polinomio original?