6.3: Trinomios factoriales

Última actualización
Guardar como PDF

Page ID: 112402

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Trinomios factoriales de la forma$x^2+bx+c$
Trinomios factoriales de la forma$ax^2+bx+c$ usando ensayo y error
Trinomios factoriales de la forma$ax^2+bx+c$ usando el método$ac$ ''
Factor usando sustitución

Antes de comenzar, toma este cuestionario de preparación.

Encuentra todos los factores de 72.
Si te perdiste este problema, revisa [enlace].
Encuentra el producto:$(3y+4)(2y+5)$.
Si te perdiste este problema, revisa [enlace].
Simplificar:$−9(6);\space −9(−6)$.
Si te perdiste este problema, revisa [enlace].

Trinomios factoriales de la Forma$x^2+bx+c$

Ya aprendiste a multiplicar binomios usando FOIL. Ahora necesitarás “deshacer” esta multiplicación. Facturar el trinomio significa comenzar con el producto, y terminar con los factores.

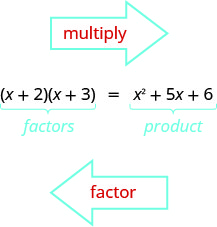
$La figura muestra la ecuación paréntesis abiertos x más 2 paréntesis cerrar paréntesis abiertos x más 3 paréntesis cercanos es igual a x cuadrado más 5 x más 6. El lado izquierdo de la ecuación está etiquetado como factores y el derecho está etiquetado como producto. Una flecha que apunta a la derecha se etiqueta multiplicar. Una flecha que apunta a la izquierda está etiquetada como factor.$

Para averiguar cómo factorizaríamos un trinomio de la forma$x^2+bx+c$, tal como$x^2+5x+6$ y factorizarlo a$(x+2)(x+3)$, comencemos con dos binomios generales de la forma$(x+m)$ y$(x+n)$.

	$(x+m)(x+n)$
Foil para encontrar el producto.	$x^{2}+m x+n x+m n$
Facturar el GCF a partir de los términos medios.	$x^{2}+(m+n) x+m n$
Nuestro trinomio es de la forma$x^2+bx+c$.	$\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}$

Esto nos dice que para factorizar un trinomio de la forma$x^2+bx+c$, necesitamos dos factores$(x+m)$ y$(x+n)$ donde los dos números$m$ y se$n$ multiplican a$c$ y se suman a$b$.

Ejemplo$\PageIndex{1}$: How to Factor a Trinomial of the form $x^2+bx+c$

Factor:$x^2+11x+24$.

Contestar: $El paso 1 es escribir los factores de x al cuadrado más 11x más 24 como dos binomios con primeros términos x. Escribir dos conjuntos de paréntesis y poner x como primer término.$ $El paso 2 es encontrar dos números m y n que se multiplican a c, m por n es c y se suman a b, m más n es b Entonces, encontrar dos números que se multipliquen a 24 y sumen a 11. Los factores de 24 son 1 y 24, 2 y 12, 3 y 8, 4 y 6. Suma de factores: 1 más 24 es 25, 2 más 12 es 14, 3 más 8 es 11 y 4 más 6 es 10.$ $El paso 3 es usar m y n, en este caso, 3 y 8, como los últimos términos de los binomios. Entonces obtenemos paréntesis abiertos x más 3 paréntesis cerrar paréntesis abiertos x más 8 paréntesis cercanos$ $El paso 4 es verificar multiplicando los factores para obtener el polinomio original.$

Ejemplo$\PageIndex{2}$

Factor:$q^2+10q+24$.

Contestar: $(q+4)(q+6)$

Ejemplo$\PageIndex{3}$

Factor:$t^2+14t+24$.

Contestar: $(t+2)(t+12)$

Resumamos los pasos que usamos para encontrar los factores.

Escribe los factores como dos binomios con los primeros términos x. $\quad \begin{array} {l} x^2+bx+c \\ (x\quad)(x\quad) \end{array} $
Encuentra dos números$m$ y$n$ eso
- multiplicar a$c$,$m·n=c$
- agregar a$b$,$m+n=b$
Uso$m$ y$n$ como los últimos términos de los factores. $\quad (x+m)(x+n)$
Verificar multiplicando los factores.

En el primer ejemplo, todos los términos en el trinomio fueron positivos. ¿Qué pasa cuando hay términos negativos? Bueno, depende qué término es negativo. Veamos primero los trinomios con solo el negativo a medio plazo.

¿Cómo se obtiene un producto positivo y una suma negativa? Usamos dos números negativos.

Ejemplo$\PageIndex{4}$

Factor:$y^2−11y+28$.

Contestar

Nuevamente, con el último término positivo$28$, y el término medio negativo$−11y$, necesitamos dos factores negativos. Encuentra dos números que se multiplican$28$ y se suman a$−11$.
$\begin{array} {ll} &y^2−11y+28 \\ \text{Write the factors as two binomials with first terms }y. &( y \quad )( y \quad ) \\ \text{Find two numbers that: multiply to }28\text{ and add to }−11.\end{array}$

Factores de$28$	Suma de factores
\ (28\)” data-valign="top">$−1,\space −28$ $−2,\space −14$ $−4,\space −7$	$−1+(−28)=−29$ $−2+(−14)=−16$ $−4+(−7)=−11^∗$

$\begin{array} {ll} \text{Use }−4,\space −7\text{ as the last terms of the binomials.} &(y−4)(y−7) \\ \text{Check:} & \\ \hspace{30mm} (y−4)(y−7) & \\ \hspace{25mm} y^2−7y−4y+28 & \\ \hspace{30mm} y^2−11y+28\checkmark & \end{array} $

Ejemplo$\PageIndex{5}$

Factor:$u^2−9u+18$.

Contestar: $(u−3)(u−6)$

Ejemplo$\PageIndex{6}$

Factor:$y^2−16y+63$.

Contestar: $(y−7)(y−9)$

Ahora bien, ¿y si el último término en el trinomio es negativo? Piensa en FOIL. El último término es producto de los últimos términos en los dos binomios. Un producto negativo resulta de multiplicar dos números con signos opuestos. Hay que tener mucho cuidado para elegir factores para asegurarse de obtener la señal correcta para el mediano plazo, también.

¿Cómo se obtiene un producto negativo y una suma positiva? Usamos un número positivo y otro negativo.

Cuando factorizamos trinomios, debemos tener los términos escritos en orden descendente, en orden desde el grado más alto hasta el grado más bajo.

Ejemplo$\PageIndex{7}$

Factor:$2x+x^2−48$.

Contestar

$\begin{array} {ll} &2x+x^2−48 \\ \text{First we put the terms in decreasing degree order.} &x^2+2x−48 \\ \text{Factors will be two binomials with first terms }x. &(x\quad)(x\quad) \end{array} $

Factores de −48−48	Suma de factores
$−1,\space 48$ $−2,\space 24$ $−3,\space 16$ $−4,\space 12$ $−6,\space 8$	$−1+48=47$ $−2+24=22$ $−3+16=13$ $−4+12=8$ $−6+8=2^∗$

$\begin{array} {ll} \text{Use }−6,\space 8\text{ as the last terms of the binomials.} &(x−6)(x+8) \\ \text{Check:} & \\ \hspace{30mm} (x−6)(x+8) & \\ \hspace{25mm} x^2−6q+8q−48 & \\ \hspace{30mm} x^2+2x−48\checkmark & \end{array} $

Ejemplo$\PageIndex{8}$

Factor:$9m+m^2+18$.

Contestar: $(m+3)(m+6)$

Ejemplo$\PageIndex{9}$

Factor:$−7n+12+n^2$.

Contestar: $(n−3)(n−4)$

A veces necesitarás factorizar trinomios de la forma$x^2+bxy+cy^2$ con dos variables, como$x^2+12xy+36y^2$. El primer término,$x^2$, es producto de los primeros términos de los factores binomiales,$x·x$. El$y^2$ en el último término significa que los segundos términos de los factores binomiales deben contener cada uno$y$. Para obtener los coeficientes$b$ y$c$, se utiliza el mismo proceso resumido en Cómo factorizar trinomios.

Ejemplo$\PageIndex{10}$

Factor:$r^2−8rs−9s^2$.

Contestar

Necesitamos$r$ en el primer término de cada binomio y$s$ en el segundo término. El último término del trinomio es negativo, por lo que los factores deben tener signos opuestos.
$\begin{array} {ll} &r^2−8rs−9s^2 \\ \text{Note that the first terms are }r,\text{last terms contain }s. &(r\quad s)(r\quad s) \\ \text{Find the numbers that multiply to }−9\text{ and add to }−8. \end{array}$

Factores de$−9$	Suma de factores
\ (−9\)” datos-valign="top">$1,\space −9$	$−1+9=8$
\ (−9\)” datos-valign="top">$−1,\space 9$	$1+(−9)=−8^∗$
\ (−9\)” datos-valign="top">$3,\space −3$	$3+(−3)=0$

$\begin{array} {ll} \text{Use }1,\space -9\text{ as coefficients of the last terms.} &(r+s)(r−9s) \\ \text{Check:} & \\ \hspace{30mm} (r−9s)(r+s) & \\ \hspace{25mm} r^2+rs−9rs−9s^2 & \\ \hspace{30mm} r^2−8rs−9s^2\checkmark & \end{array} $

Ejemplo$\PageIndex{11}$

Factor:$a^2−11ab+10b^2$.

Contestar: $(a−b)(a−10b)$

Ejemplo$\PageIndex{12}$

Factor:$m^2−13mn+12n^2$.

Contestar: $(m−n)(m−12n)$

Algunos trinomios son primos. La única manera de estar seguro de un trinomio es prime es enumerar todas las posibilidades y demostrar que ninguna de ellas funciona.

Ejemplo$\PageIndex{13}$

Factor:$u^2−9uv−12v^2$.

Contestar

Necesitamos$u$ en el primer término de cada binomio y$v$ en el segundo término. El último término del trinomio es negativo, por lo que los factores deben tener signos opuestos.
$\begin{array} {ll} &u^2−9uv−12v^2 \\ \text{Note that the first terms are }u,\text{ last terms contain }v. &(u\quad v)(u\quad v) \\ \text{Find the numbers that multiply to }−12\text{ and add to }−9. & \end{array} $

Factores de$−12$	Suma de factores
\ (−12\)” datos-valign="top">$1,−12$ $−1,12$ $2,−6$ $−2,6$ $3,−4$ $−3,4$	$1+(−12)=−11$ $−1+12=11$ $2+(−6)=−4$ $−2+6=4$ $3+(−4)=−1$ $−3+4=1$

Tenga en cuenta que no hay pares de factores que nos den$−9$ como suma. El trinomio es primo.

Ejemplo$\PageIndex{14}$

Factor:$x^2−7xy−10y^2$.

Contestar: prime

Ejemplo$\PageIndex{15}$

Factor:$p^2+15pq+20q^2$.

Contestar: prime

Resumamos el método que acabamos de desarrollar para facturar trinomios de la forma$x^2+bx+c$.

ESTRATEGIA PARA FACTORAR TRINOMIOS DE LA FORMA$x^2+bx+c$

Cuando factorizamos un trinomio, miramos primero los signos de sus términos para determinar los signos de los factores binomiales.

	$ x^{2}+b x+c $
	$ (x+m)(x+n) $
Cuando$ c $ es positivo,$ m $ y$ n $ tienen el mismo signo.
$ b $positivo		$ b $negativo
$ m,n $positivo		$ m,n $negativo
$ x^{2}+5 x+6 $		$ x^{2}-6 x+8 $
$ (x+2)(x+3) $		$ (x-4)(x-2) $
mismos signos		mismos signos
Cuando$ c $ es negativo,$ m $ y$ n $ tienen el signo contrario.
$ x^{2}+x-12 $		$ x^{2}-2 x-15 $
$ (x+4)(x-3) $		$ (x-5)(x+3) $
signos opuestos		signos opuestos

Observe que, en el caso cuando$m$ y$n$ tengan signos opuestos, el signo del que tiene el valor absoluto mayor coincide con el signo de$b$.

Trinomios factoriales de la forma ax ² + bx + c usando Prueba y Error

Nuestro siguiente paso es factorizar trinomios cuyo coeficiente principal no es 1, trinomios de la forma$ax^2+bx+c$.

¡Recuerda siempre verificar primero un GCF! A veces, después de factorizar el GCF, el coeficiente principal del trinomio se vuelve$1$ y puedes factorizarlo por los métodos que hemos utilizado hasta ahora. Hagamos un ejemplo para ver cómo funciona esto.

Ejemplo$\PageIndex{16}$

Factor completamente:$4x^3+16x^2−20x$.

Contestar

$\begin{array} {lll} \text{Is there a greatest common factor?} &\qquad &4x^3+16x^2−20x \\ \quad \text{Yes, }GCF=4x.\text{ Factor it.} & &4x(x^2+4x−5) \\ & & \\ & & \\ \text{Binomial, trinomial, or more than three terms?} & & \\ \quad \text{It is a trinomial. So “undo FOIL.”} & &4x(x\quad)(x\quad) \\ & & \\ & & \\ \text{Use a table like the one shown to find two numbers that} & &4x(x−1)(x+5) \\ \text{multiply to }−5\text{ and add to }4. & & \\ & & \\ & & \end{array} $

Factores de$−5$	Suma de factores
\ (−5\)” datos-valign="top">$−1,5$ $1,−5$	$−1+5=4^∗$ $1+(−5)=−4$

$\begin{array} {l} \text{Check:}\\ \hspace{27mm}4x(x−1)(x+5) \\ \hspace{25mm} 4x(x^2+5x−x−5) \\ \hspace{30mm} 4x(x^2+4x−5) \\ \hspace{25mm} 4x^3+16x2−20x\checkmark \end{array} $

Ejemplo$\PageIndex{17}$

Factor completamente:$5x^3+15x^2−20x$.

Contestar: $5x(x−1)(x+4)$

Ejemplo$\PageIndex{18}$

Factor completamente:$6y^3+18y^2−60y$.

Contestar: $6y(y−2)(y+5)$

¿Qué sucede cuando el coeficiente principal no es$1$ y no hay GCF? Existen varios métodos que se pueden utilizar para factorizar estos trinomios. Primero usaremos el método de Prueba y Error.

Facturemos el trinomio$3x^2+5x+2$.

De nuestro trabajo anterior, esperamos que esto se factorizará en dos binomios.

\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]

Sabemos que los primeros términos de los factores binomiales se multiplicarán para darnos$3x^2$. Los únicos factores de$3x^2$ son$1x,\space 3x$. Podemos colocarlos en los binomios.

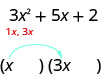
$El polinomio es 3x al cuadrado más 5x más 2. Hay dos pares de paréntesis, siendo los primeros términos en ellos x y 3x.$

Cheque: ¿Lo hace$1x·3x=3x^2$?

Sabemos que los últimos términos de los binomios se multiplicarán a$2$. Dado que este trinomio tiene todos los términos positivos, solo necesitamos considerar factores positivos. Los únicos factores de$2$ son$1$ y$2$. Pero ahora tenemos dos casos a considerar ya que marcará la diferencia si escribimos$1$,$2$ o$2$,$1$.

¿Qué factores son correctos? Para decidir eso, multiplicamos los términos interno y externo.

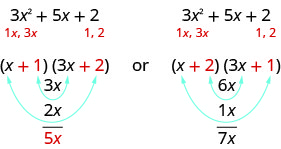
$La figura muestra el polinomio 3x cuadrado más 5x más 2 y dos posibles pares de factores. Uno es paréntesis abiertos x más 1 paréntesis cerrar paréntesis abiertos 3x más 2 paréntesis de cierre. El otro es paréntesis abiertos x más 2 paréntesis cerrar paréntesis abiertos 3x más 1 paréntesis cerrar. En cada caso, se muestran flechas emparejando el primer término del primer factor con el último término del segundo factor y el primer término del segundo factor con el último término del primer factor.$

Dado que el término medio del trinomio es$5x$, los factores en el primer caso funcionarán. Usemos FOIL para verificar.

\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]

Nuestro resultado del factoring es:

\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]

Ejemplo$\PageIndex{19}$: How to Factor a Trinomial Using Trial and Error

Facturar completamente usando prueba y error:$3y^2+22y+7$.

Contestar: $El paso 1 es escribir el trinomio en orden descendente. El trinomio 3 y al cuadrado más 22 años más 7 ya está en orden descendente.$ $El paso 2 es factorizar el GCF. Aquí, no hay ninguno.$ $El paso 3 es Buscar todos los pares de factores del primer término. Los únicos factores aquí son 1y y 3y. Como sólo hay un par, podemos poner cada uno como primer término entre paréntesis.$ $El paso 4 es encontrar todos los pares de factores del tercer término. Aquí, el único par es 1 y 7.$ $El paso 5 consiste en probar todas las combinaciones posibles de los factores hasta encontrar el producto correcto. Para posibles factores abrir paréntesis y más 1 paréntesis cerrar paréntesis abiertos 37 más 7 paréntesis de cierre, el producto es 3 y al cuadrado más 10y más 7. Para los posibles factores abrir paréntesis y más 7 paréntesis cerrar paréntesis abiertos 3y más 1 paréntesis cerrar, el producto es 3 y cuadrado más 22y más 7, que es el producto correcto. De ahí que los factores correctos son paréntesis abiertos y más 7 paréntesis cercanos paréntesis abiertos 3y más 1 paréntesis cerrar.$ $El paso 6 es verificar multiplicando.$

Ejemplo$\PageIndex{20}$

Facturar completamente usando prueba y error:$2a^2+5a+3$.

Contestar: $(a+1)(2a+3)$

Ejemplo$\PageIndex{21}$

Facturar completamente usando prueba y error:$4b^2+5b+1$.

Contestar: $(b+1)(4b+1)$

TRINOMIOS FACTORIALES DE LA FORMA$ax^2+bx+c$ USING TRIAL AND ERROR.

Escribir el trinomio en orden descendente de grados según sea necesario.
Factorial cualquier GCF.
Encuentra todos los pares de factores del primer término.
Encuentra todos los pares de factores del tercer término.
Pruebe todas las combinaciones posibles de los factores hasta encontrar el producto correcto.
Verificar multiplicando.

Recuerde, cuando el término medio es negativo y el último término es positivo, los signos en los binomios deben ser ambos negativos.

Ejemplo$\PageIndex{22}$

Facturar completamente usando prueba y error:$6b^2−13b+5$.

Contestar

El trinomio ya está en orden descendente.	$.$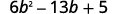
Encuentra los factores del primer término.	$.$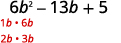
Encuentra los factores del último término. Considera las señales. Desde el último término,$5$, es positivo sus factores deben ser ambos positivos o ambos ser negativos. El coeficiente del término medio es negativo, por lo que utilizamos los factores negativos.	$.$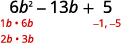

Considera todas las combinaciones de factores.

$6b^2−13b+5$
Posibles factores	Producto
\ (6b^2−13b+5\) Factores posibles” data-valign="top">$(b−1)(6b−5)$	\ (6b^2−13b+5\) Producto” data-valign="top">$6b^2−11b+5$
\ (6b^2−13b+5\) Factores posibles” data-valign="top">$(b−5)(6b−1)$	\ (6b^2−13b+5\) Producto” data-valign="top">$6b^2−31b+5$
\ (6b^2−13b+5\) Factores posibles” data-valign="top">$(2b−1)(3b−5)$	\ (6b^2−13b+5\) Producto” data-valign="middle">$6b^2−13b+5^∗$
\ (6b^2−13b+5\) Factores posibles” data-valign="top">$(2b−5)(3b−1)$	\ (6b^2−13b+5\) Producto” data-valign="middle">$6b^2−17b+5$

$\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} $

Ejemplo$\PageIndex{23}$

Facturar completamente usando prueba y error:$8x^2−14x+3$.

Contestar: $(2x−3)(4x−1)$

Ejemplo$\PageIndex{24}$

Facturar completamente usando prueba y error:$10y^2−37y+7$.

Contestar: $(2y−7)(5y−1)$

Cuando facetamos una expresión, siempre buscamos primero un factor común más grande. Si la expresión no tiene un mayor factor común, tampoco puede haber uno en sus factores. Esto puede ayudarnos a eliminar algunas de las posibles combinaciones de factores.

Ejemplo$\PageIndex{25}$

Facturar completamente usando prueba y error:$18x^2−37xy+15y^2$.

Contestar

El trinomio ya está en orden descendente.	$.$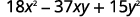
Encuentra los factores del primer término.	$.$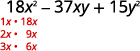
Encuentra los factores del último término. Considera las señales. Dado que 15 es positivo y el coeficiente del término medio es negativo, utilizamos los factores negativos.	$.$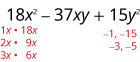

Considera todas las combinaciones de factores.

$En esta tabla se muestran los posibles factores y productos correspondientes del trinomio 18 x cuadrado menos 37xy más 15 y al cuadrado. En algunos pares de factores, cuando un factor contiene dos términos con un factor común, ese factor se resalta. En tales casos, el producto no es una opción porque si el trinomio no tiene factores comunes, entonces ninguno de los factores puede contener un factor común. Factor: abrir paréntesis x menos 1y cerrar paréntesis abrir paréntesis 18x menos 15y cerrar paréntesis, resaltado. Factor, paréntesis abiertos x menos 15y paréntesis cerrar paréntesis abiertos 18x menos 1y paréntesis cerrar; producto: 18 x cuadrado menos 271xy más 15 y al cuadrado. Factor paréntesis abiertos x menos 3y paréntesis cerrar paréntesis abiertos 18x menos 5 y cerrar paréntesis; producto: 18 x cuadrado menos 59xy más 15 y cuadrado. Factor: abrir paréntesis x menos 5y cerrar paréntesis abrir paréntesis 18x menos 3y cerrar paréntesis resaltados. Factor: abrir paréntesis 2x menos 1y cerrar paréntesis abrir paréntesis 9x menos 15y cerrar paréntesis resaltados. Factor: paréntesis abiertos 2x menos 15y paréntesis cerrar paréntesis abiertos 9x menos 1y paréntesis cerrar; producto 18 x cuadrado menos 137 xy más 15y cuadrado. Factor: paréntesis abiertos 2x menos 3y paréntesis cerrar paréntesis abiertos 9x menos 5y paréntesis cerrar; producto: 18 x cuadrado menos 37xy más 15 y al cuadrado, que es el trinomio original. Factor: abrir paréntesis 2x menos 57 cerrar paréntesis abrir paréntesis 9x menos 3y cerrar paréntesis resaltados. Factor: abrir paréntesis 3x menos 1y cerrar paréntesis abrir paréntesis 6x menos 15y cerrar paréntesis resaltados. Factor: abrir paréntesis 3x menos 15y cerrar paréntesis resaltados paréntesis abiertos 6x menos 1y cerrar paréntesis. Factor: paréntesis abiertos 3x menos 3y cerrar paréntesis resaltados paréntesis abiertos 6x menos 5y.$

$\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} $

Ejemplo$\PageIndex{26}$

Facturar completamente usando prueba y error$18x^2−3xy−10y^2$.

Contestar: $(3x+2y)(6x−5y)$

Ejemplo$\PageIndex{27}$

Facturar completamente usando prueba y error:$30x^2−53xy−21y^2$.

Contestar: $(3x+y)(10x−21y)$

No olvides buscar primero un GCF y recordar si el coeficiente principal es negativo, también lo es el GCF.

Ejemplo$\PageIndex{28}$

Facturar completamente usando prueba y error:$−10y^4−55y^3−60y^2$.

Contestar

	$.$
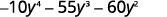
Observe el mayor factor común, entonces factírelo primero.	$.$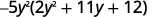
Factorial el trinomio.	$.$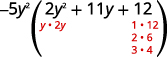

Considera todas las combinaciones.

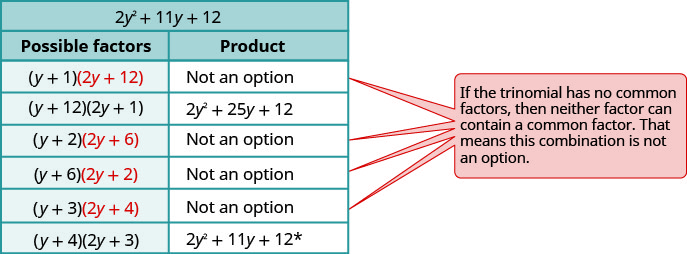
$En esta tabla se muestran los posibles factores y producto del trinomio 2 y al cuadrado más 11 años más 12. En algunos pares de factores, cuando un factor contiene dos términos con un factor común, ese factor se resalta. En tales casos, el producto no es una opción porque si el trinomio no tiene factores comunes, entonces ninguno de los factores puede contener un factor común. Factor: y más 1, 2y más 12 resaltados. Factor: y más 12, 2y más 1; producto: 2 y al cuadrado más 25 años más 12. Factor: y más 2, 2y más 6 resaltados. Factor: y más 6, 2y más 2 resaltados. Factor: y más 3, 2y más 4 resaltados. Factor: y más 4, 2y más 3; producto: 2 y al cuadrado más 11 años más 12. Este es el trinomio original.$

$\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} $

Ejemplo$\PageIndex{29}$

Facturar completamente usando prueba y error:$15n^3−85n^2+100n$.

Contestar: $5n(n−4)(3n−5)$

Ejemplo$\PageIndex{30}$

Facturar completamente usando prueba y error:$56q^3+320q^2−96q$.

Contestar: $8q(q+6)(7q−2)$

Trinomios factoriales de la Forma$ax^2+bx+c$ usando el Método “$ac$”

Otra forma de facturar trinomios de la forma$ax^2+bx+c$ es el método “$ac$”. (El método “$ac$” a veces se llama el método de agrupación.) El método “$ac$” es en realidad una extensión de los métodos que utilizó en la última sección para factorizar trinomios con coeficiente inicial uno. Este método es muy estructurado (eso es paso a paso), ¡y siempre funciona!

Ejemplo$\PageIndex{31}$: How to Factor Trinomials using the “ac” Method

Factor usando el método “$ac$”:$6x^2+7x+2$.

Contestar: $El paso 1 es factorizar el GCF. No hay ninguno en 6 x al cuadrado más 7x más 2.$ $El paso 2 es encontrar el producto de a y c. El producto de 6 y 2 es 12.$ $El paso 3 es encontrar 2 números m y n tal que mn es ac y m más n es b. entonces necesitamos números que se multipliquen a 12 y sumen a 7. Ambos factores deben ser positivos. 3 veces 4 es 12 y 3 más 4 es 7.$ $El paso 4 es dividir el término medio usando m y n. Así que reescribimos 7 x como 3x más 4x. Daría el mismo resultado si usáramos 4x más 3x. Reescribiendo, obtenemos 6 x al cuadrado más 3x más 4x más 2. Observe que esto es lo mismo que el polinomio original. Acabamos de dividir el término medio para obtener una forma más útil$ $El paso 5 es factorial por agrupación. Entonces, obtenemos, 3x paréntesis abiertos 2x más 1 paréntesis cerrar más 2 paréntesis abiertos 2x más 1 paréntesis cerrar. Esto es igual a 2x más 1, 3x más 2.$ $El paso 6 es verificar multiplicando los factores.$

Ejemplo$\PageIndex{32}$

Factor usando el método “$ac$”:$6x^2+13x+2$.

Contestar: $(x+2)(6x+1)$

Ejemplo$\PageIndex{33}$

Factor usando el método “$ac$”:$4y^2+8y+3$.

Contestar: $(2y+1)(2y+3)$

Aquí se resume el método “$ac$”.

TRINOMIOS FACTORIALES DE LA FORMA$ax^2+bx+c$ USING THE “$ac$” METHOD.

Factorial cualquier GCF.
Encuentra el producto$ac$.
Encuentra dos números$m$ y$n$ que:
$\begin{array} {ll} \text{Multiply to }ac &m·n=a·c \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} $
Dividir el término medio usando$m$ y$n$. $ax^2+mx+nx+c$
Factor por agrupación.
Verificar multiplicando los factores.

¡No olvides buscar un factor común!

Ejemplo$\PageIndex{34}$

Factor usando el método '“$ac$”:$10y^2−55y+70$.

Contestar

¿Hay un factor común más grande?
Sí. El GCF es$5$.		$.$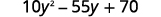
Factorial.		$.$
El trinomio dentro de los paréntesis tiene un coeficiente principal que no lo es$1$.		$.$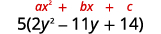
Encuentra el producto$ac$.	$ac=28$
Encuentra dos números que se multiplican a$ac$	$(−4)(−7)=28$
y agregar a$b$.	$−4(−7)=−11$
Dividir el término medio.		$.$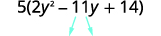
		$.$
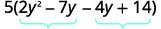
Facturar el trinomio por agrupación.		$.$
		$.$
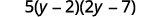
Verifique multiplicando los tres factores. $\hspace{50mm} 5(y−2)(2y−7)$ $\hspace{45mm} 5(2y^2−7y−4y+14)$ $\hspace{48mm} 5(2y^2−11y+14)$ $\hspace{49mm} 10y^2−55y+70\checkmark$

Ejemplo$\PageIndex{35}$

Factor usando el método “$ac$”:$16x^2−32x+12$.

Contestar: $4(2x−3)(2x−1)$

Ejemplo$\PageIndex{36}$

Factor usando el método “$ac$”:$18w^2−39w+18$.

Contestar: $3(3w−2)(2w−3)$

Factor mediante sustitución

A veces un trinomio no parece estar en la$ax^2+bx+c$ forma. Sin embargo, a menudo podemos hacer una sustitución reflexiva que nos permitirá que se ajuste a la$ax^2+bx+c$ forma. A esto se le llama factorización por sustitución. Es estándar usar$u$ para la sustitución.

En el$ax^2+bx+c$, el término medio tiene una variable,$x$, y su cuadrado$x^2$,, es la parte variable del primer término. Busca esta relación mientras intentas encontrar una sustitución.

Ejemplo$\PageIndex{37}$

Factor por sustitución:$x^4−4x^2−5$.

Contestar

La parte variable del término medio es$x^2$ y su cuadrado,$x^4$, es la parte variable del primer término. (Ya sabemos$(x^2)^2=x^4)$. Si lo dejamos$u=x^2$, podemos poner nuestro trinomio en la$ax^2+bx+c$ forma que necesitamos para faccionarlo.

	$x^4−4x^2−5$
Reescribir el trinomio para prepararse para la sustitución.	$(x^2)^2−4(x^2)-5$
Dejar$u=x^2$ y sustituir.	$(u)^2−4(u)-5$
Factorial el trinomio.	$(u+1)(u-5)$
Reemplazar$u$ con$x^2$.	$(x^2+1)(x^2-5)$
Comprobar: $\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}$

Ejemplo$\PageIndex{38}$

Factor por sustitución:$h^4+4h^2−12$.

Contestar: $(h^2−2)(h^2+6)$

Ejemplo$\PageIndex{39}$

Factor por sustitución:$y^4−y^2−20$.

Contestar: $(y^2+4)(y^2−5)$

A veces la expresión a sustituir no es un monomio.

Ejemplo$\PageIndex{40}$

Factor por sustitución:$(x−2)^2+7(x−2)+12$

Contestar

El binomio en el término medio,$(x−2)$ es cuadrado en el primer término. Si dejamos$u=x−2$ y sustituimos, nuestro trinomio estará en$ax^2+bx+c$ forma.

	$.$
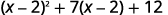
Reescribir el trinomio para prepararse para la sustitución.	$.$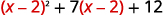
Dejar$u=x−2$ y sustituir.	$.$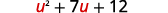
Factorial el trinomio.	$.$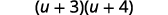
Reemplazar$u$ con$x−2$.	$.$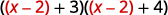
Simplifica dentro de los paréntesis.	$.$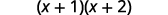

Esto también podría factorizarse multiplicando primero el$(x−2)^2$ y el$7(x−2)$ y luego combinando términos similares y luego factorizando. La mayoría de los estudiantes prefieren el método de sustitución.

Ejemplo$\PageIndex{41}$

Factor por sustitución:$(x−5)^2+6(x−5)+8$.

Contestar: $(x−3)(x−1)$

Ejemplo$\PageIndex{42}$

Factor por sustitución:$(y−4)^2+8(y−4)+15$.

Contestar: $(y−1)(y+1)$

Vea este video para obtener instrucciones y prácticas adicionales con el factoring.

Conceptos clave

Cómo factorizar trinomios de la forma$x^2+bx+c$.
1. Escribe los factores como dos binomios con los primeros términos x. $\quad \begin{array} (l) x^2+bx+c \\ (x\quad)(x\quad)\end{array}$
2. Encuentra dos números$m$ y$n$ eso
  $\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}$
3. Uso$m$ y$n$ como los últimos términos de los factores. $\qquad (x+m)(x+n)$
4. Verificar multiplicando los factores.
Estrategia para Factorizar Trinomios de la Forma$x^2+bx+c$: Cuando factorizamos un trinomio, analizamos primero los signos de sus términos para determinar los signos de los factores binomiales.

Para trinomios de la forma:$x^2+bx+c = (x+m)(x+n)$

Cuando$c$ es positivo,$m$ y$n$ debe tener el mismo signo (y este será el signo de$b$ ).

Ejemplos:$x^2+5x+6=(x+2)(x+3)$,$x^2−6x+8 = (x−4)(x−2)$

Cuando$c$ es negativo,$m$ y$n$ tienen signos opuestos. El mayor de$m$ y$n$ tendrá el signo de$b$.

Ejemplos:$x^2+x−12=(x+4)(x−3)$,$x^2−2x−15=(x−5)(x+3)$

Observe que, en el caso cuando$m$ y$n$ tengan signos opuestos, el signo del que tiene el valor absoluto mayor coincide con el signo de$b$.
Cómo factorial trinomios de la forma$ax^2+bx+c$ usando ensayo y error.
1. Escribir el trinomio en orden descendente de grados según sea necesario.
2. Factorial cualquier GCF.
3. Encuentra todos los pares de factores del primer término.
4. Encuentra todos los pares de factores del tercer término.
5. Pruebe todas las combinaciones posibles de los factores hasta encontrar el producto correcto.
6. Verificar multiplicando.
Cómo factorial trinomios de la forma$ax^2+bx+c$ usando el método “$ac$”.
1. Factorial cualquier GCF.
2. Encuentra el producto$ac$.
3. Encuentra dos números$m$ y$n$ que:
  $\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}$
4. Dividir el término medio usando$m$ y$n$. $\quad ax^2+mx+nx+c$
5. Factor por agrupación.
6. Verificar multiplicando los factores.

	\((x+m)(x+n)\)
Foil para encontrar el producto.	\(x^{2}+m x+n x+m n\)
Facturar el GCF a partir de los términos medios.	\(x^{2}+(m+n) x+m n\)
Nuestro trinomio es de la forma\(x^2+bx+c\).	\(\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}\)

Factores de\(−9\)	Suma de factores
\ (−9\)” datos-valign="top">\(1,\space −9\)	\(−1+9=8\)
\ (−9\)” datos-valign="top">\(−1,\space 9\)	\(1+(−9)=−8^∗\)
\ (−9\)” datos-valign="top">\(3,\space −3\)	\(3+(−3)=0\)

	\( x^{2}+b x+c \)
	\( (x+m)(x+n) \)
Cuando\( c \) es positivo,\( m \) y\( n \) tienen el mismo signo.
\( b \)positivo		\( b \)negativo
\( m,n \)positivo		\( m,n \)negativo
\( x^{2}+5 x+6 \)		\( x^{2}-6 x+8 \)
\( (x+2)(x+3) \)		\( (x-4)(x-2) \)
mismos signos		mismos signos
Cuando\( c \) es negativo,\( m \) y\( n \) tienen el signo contrario.
\( x^{2}+x-12 \)		\( x^{2}-2 x-15 \)
\( (x+4)(x-3) \)		\( (x-5)(x+3) \)
signos opuestos		signos opuestos

\(6b^2−13b+5\)
Posibles factores	Producto
\ (6b^2−13b+5\) Factores posibles” data-valign="top">\((b−1)(6b−5)\)	\ (6b^2−13b+5\) Producto” data-valign="top">\(6b^2−11b+5\)
\ (6b^2−13b+5\) Factores posibles” data-valign="top">\((b−5)(6b−1)\)	\ (6b^2−13b+5\) Producto” data-valign="top">\(6b^2−31b+5\)
\ (6b^2−13b+5\) Factores posibles” data-valign="top">\((2b−1)(3b−5)\)	\ (6b^2−13b+5\) Producto” data-valign="middle">\(6b^2−13b+5^∗\)
\ (6b^2−13b+5\) Factores posibles” data-valign="top">\((2b−5)(3b−1)\)	\ (6b^2−13b+5\) Producto” data-valign="middle">\(6b^2−17b+5\)

	\(x^4−4x^2−5\)
Reescribir el trinomio para prepararse para la sustitución.	\((x^2)^2−4(x^2)-5\)
Dejar\(u=x^2\) y sustituir.	\((u)^2−4(u)-5\)
Factorial el trinomio.	\((u+1)(u-5)\)
Reemplazar\(u\) con\(x^2\).	\((x^2+1)(x^2-5)\)
Comprobar: \(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\)

¿Hay un factor común más grande?
Sí. El GCF es\(5\).		$.$
Factorial.		$.$
El trinomio dentro de los paréntesis tiene un coeficiente principal que no lo es\(1\).		$.$
Encuentra el producto\(ac\).	\(ac=28\)
Encuentra dos números que se multiplican a\(ac\)	\((−4)(−7)=28\)
y agregar a\(b\).	\(−4(−7)=−11\)
Dividir el término medio.		$.$
		$.$
Facturar el trinomio por agrupación.		$.$
		$.$
Verifique multiplicando los tres factores. \(\hspace{50mm} 5(y−2)(2y−7)\) \(\hspace{45mm} 5(2y^2−7y−4y+14)\) \(\hspace{48mm} 5(2y^2−11y+14)\) \(\hspace{49mm} 10y^2−55y+70\checkmark\)

	$.$
Reescribir el trinomio para prepararse para la sustitución.	$.$
Dejar\(u=x−2\) y sustituir.	$.$
Factorial el trinomio.	$.$
Reemplazar\(u\) con\(x−2\).	$.$
Simplifica dentro de los paréntesis.	$.$

Objetivos de aprendizaje

Trinomios factoriales de la Forma\(x^2+bx+c\)

Ejemplo\(\PageIndex{1}\): How to Factor a Trinomial of the form \(x^2+bx+c\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\)

Ejemplo\(\PageIndex{9}\)

Ejemplo\(\PageIndex{10}\)

Ejemplo\(\PageIndex{11}\)

Ejemplo\(\PageIndex{12}\)

Ejemplo\(\PageIndex{13}\)

Ejemplo\(\PageIndex{14}\)

Ejemplo\(\PageIndex{15}\)

ESTRATEGIA PARA FACTORAR TRINOMIOS DE LA FORMA\(x^2+bx+c\)

Trinomios factoriales de la forma ax 2 + bx + c usando Prueba y Error

Ejemplo\(\PageIndex{16}\)

Ejemplo\(\PageIndex{17}\)

Ejemplo\(\PageIndex{18}\)

Ejemplo\(\PageIndex{19}\): How to Factor a Trinomial Using Trial and Error

Ejemplo\(\PageIndex{20}\)

Ejemplo\(\PageIndex{21}\)

TRINOMIOS FACTORIALES DE LA FORMA\(ax^2+bx+c\) USING TRIAL AND ERROR.

Ejemplo\(\PageIndex{22}\)

Ejemplo\(\PageIndex{23}\)

Ejemplo\(\PageIndex{24}\)

Ejemplo\(\PageIndex{25}\)

Ejemplo\(\PageIndex{26}\)

Ejemplo\(\PageIndex{27}\)

Ejemplo\(\PageIndex{28}\)

Ejemplo\(\PageIndex{29}\)

Ejemplo\(\PageIndex{30}\)

Trinomios factoriales de la Forma\(ax^2+bx+c\) usando el Método “\(ac\)”

Ejemplo\(\PageIndex{31}\): How to Factor Trinomials using the “ac” Method

Ejemplo\(\PageIndex{32}\)

Ejemplo\(\PageIndex{33}\)

TRINOMIOS FACTORIALES DE LA FORMA\(ax^2+bx+c\) USING THE “\(ac\)” METHOD.

Ejemplo\(\PageIndex{34}\)

Ejemplo\(\PageIndex{35}\)

Ejemplo\(\PageIndex{36}\)

Factor mediante sustitución

Ejemplo\(\PageIndex{37}\)

Ejemplo\(\PageIndex{38}\)

Ejemplo\(\PageIndex{39}\)

Ejemplo\(\PageIndex{40}\)

Ejemplo\(\PageIndex{41}\)

Ejemplo\(\PageIndex{42}\)

Conceptos clave

Trinomios factoriales de la forma ax ² + bx + c usando Prueba y Error