9.2: Resolver ecuaciones cuadráticas usando la propiedad de raíz cuadrada
- Page ID
- 112590
Al final de esta sección, podrás:
- Resolver ecuaciones cuadráticas de la forma\(ax^{2}=k\) usando la Propiedad Raíz Cuadrada
- Resolver ecuaciones cuadráticas de la forma\(a(x–h)^{2}=k\) usando la Propiedad Raíz Cuadrada
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(\sqrt{128}\).
Si te perdiste este problema, revisa el Ejemplo 8.13. - Simplificar:\(\sqrt{\frac{32}{5}}\).
Si te perdiste este problema, revisa el Ejemplo 8.50. - Factor:\(9 x^{2}-12 x+4\).
Si te perdiste este problema, revisa el Ejemplo 6.23.
Una ecuación cuadrática es una ecuación de la forma\(a x^{2}+b x+c=0\), donde\(a≠0\). Las ecuaciones cuadráticas difieren de las ecuaciones lineales al incluir un término cuadrático con la variable elevada a la segunda potencia de la forma\(ax^{2}\). Utilizamos diferentes métodos para resolver ecuaciones cuadráticas que las lineales, porque solo sumar, restar, multiplicar y dividir términos no aislarán la variable.
Hemos visto que algunas ecuaciones cuadráticas pueden resolverse factorizando. En este capítulo, aprenderemos otros tres métodos para usar en caso de que no se pueda factorizar una ecuación cuadrática.
Resolver Ecuaciones Cuadráticas de la Forma\(ax^{2}=k\) usando la Propiedad Raíz Cuadrada
Ya hemos resuelto algunas ecuaciones cuadráticas por factorización. Revisemos cómo se utilizó el factoring para resolver la ecuación cuadrática\(x^{2}=9\).
\(x^{2}=9\)
Poner la ecuación en forma estándar.
\(x^{2}-9=0\)
Factorice la diferencia de cuadrados.
\((x-3)(x+3)=0\)
Utilice la Propiedad Cero Produce.
\(x-3=0 \quad x-3=0\)
Resuelve cada ecuación.
\(x=3 \quad x=-3\)
Podemos usar fácilmente el factoring para encontrar las soluciones de ecuaciones similares, como\(x^{2}=16\) y\(x^{2}=25\), porque\(16\) y\(25\) son cuadrados perfectos. En cada caso, obtendríamos dos soluciones,\(x=4, x=-4\) y\(x=5, x=-5\)
Pero, ¿qué pasa cuando tenemos una ecuación como\(x^{2}=7\)? Como no\(7\) es un cuadrado perfecto, no podemos resolver la ecuación factorizando.
Anteriormente aprendimos que ya que\(169\) es el cuadrado de\(13\), también podemos decir que\(13\) es una raíz cuadrada de\(169\). También,\((-13)^{2}=169\), también lo\(−13\) es una raíz cuadrada de\(169\). Por lo tanto, ambos\(13\) y\(−13\) son raíces cuadradas de\(169\). Entonces, cada número positivo tiene dos raíces cuadradas, una positiva y otra negativa. Anteriormente definimos la raíz cuadrada de un número de esta manera:
Si\(n^{2}=m\), entonces\(n\) es una raíz cuadrada de\(m\).
Dado que estas ecuaciones son todas de la forma\(x^{2}=k\), la definición de raíz cuadrada nos dice que las soluciones son las dos raíces cuadradas de\(k\). Esto lleva a la Propiedad de Raíz Cuadrada.
Propiedad Raíz Cuadrada
Si\(x^{2}=k\), entonces
\(x=\sqrt{k} \quad\)o\(\quad x=-\sqrt{k} \quad\) o\(\quad x=\pm \sqrt{k}\)
Observe que la Propiedad Raíz Cuadrada da dos soluciones a una ecuación de la forma\(x^{2}=k\), la raíz cuadrada principal de\(k\) y su opuesta. También podríamos escribir la solución como\(x=\pm \sqrt{k}\). Leemos esto como\(x\) igual positivo o negativo a la raíz cuadrada de\(k\).
Ahora vamos a resolver de\(x^{2}=9\) nuevo la ecuación, esta vez usando la Propiedad Raíz Cuadrada.
\(\begin{aligned} &x^{2} =9 \\ \text { Use the Square Root Property. } \quad& x=\pm \sqrt{9} \\& x =\pm 3 \end{aligned}\)
Así\(x=3\) o\(x=-3\)
¿Qué pasa cuando la constante no es un cuadrado perfecto? Usemos la Propiedad Raíz Cuadrada para resolver la ecuación\(x^{2}=7\).
\(x^{2}=7\)
Utilice la Propiedad Raíz Cuadrada. \(x=\sqrt{7}, \quad x=-\sqrt{7}\)
No podemos simplificar\(\sqrt{7}\), así que dejamos la respuesta como radical.
Resolver:\(x^{2}-50=0\).
Solución:
| Paso 1: Aislar el término cuadrático y hacer su coeficiente uno. | Agrega\(50\) a ambos lados para conseguir\(x^{2}\) por sí mismo. | \(\begin{aligned} x^{2}-50 &=0 \\ x^{2} &=50 \end{aligned}\) |
| Paso 2: Utilice la Propiedad Raíz Cuadrada. | Recuerda escribir el\(\pm\) símbolo. | \(x=\pm \sqrt{50}\) |
| Paso 3: Simplificar el radical. | Reescribe para mostrar dos soluciones. | \(\begin{array}{l}{x=\pm \sqrt{25} \cdot \sqrt{2}} \\ {x=\pm 5 \sqrt{2}} \\ {}x=5\sqrt{2}, \:x=-5\sqrt{2}\end{array}\) |
| Paso 4: Consulta las soluciones. | Sustituto en\(x=5 \sqrt{2}\) y\(x=-5 \sqrt{2}\) |
\(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) \(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{-5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) |
Resolver:\(x^{2}-48=0\).
- Contestar
-
\(x=4 \sqrt{3}, x=-4 \sqrt{3}\)
Resolver:\(y^{2}-27=0\).
- Contestar
-
\(y=3 \sqrt{3}, y=-3 \sqrt{3}\)
Los pasos a seguir para usar la Propiedad Raíz Cuadrada para resolver una ecuación cuadrática se enumeran aquí.
Resolver una ecuación cuadrática usando la propiedad de raíz cuadrada
- Aísle el término cuadrático y haga su coeficiente uno.
- Utilice la Propiedad Raíz Cuadrada.
- Simplifica lo radical.
- Consulta las soluciones.
Para utilizar la Propiedad Raíz Cuadrada, el coeficiente del término variable debe ser igual a uno. En el siguiente ejemplo, debemos dividir ambos lados de la ecuación por el coeficiente\(3\) antes de usar la Propiedad Raíz Cuadrada.
Resolver:\(3 z^{2}=108\).
Solución:
| \(3 z^{2}=108\) | |
| El término cuadrático es aislado. Dividir por\(3\) para hacer su coeficiente\(1\). | \(\frac{3 z^{2}}{3}=\frac{108}{3}\) |
| Simplificar. | \(z^{2}=36\) |
| Utilice la Propiedad Raíz Cuadrada. | \(z=\pm \sqrt{36}\) |
| Simplifica lo radical. | \(z=\pm 6\) |
| Reescribe para mostrar dos soluciones. | \(z=6, \quad z=-6\) |
|
Consulta las soluciones: 
|
Resolver:\(2x^{2}=98\).
- Contestar
-
\(x=7, x=-7\)
Resolver:\(5m^{2}=80\).
- Contestar
-
\(m=4, m=-4\)
La Propiedad Raíz Cuadrada establece 'Si\(x^{2}=k\), '¿Qué pasará si\(k<0\)? Este será el caso en el siguiente ejemplo.
Resolver:\(x^{2}+72=0\).
Solución:
| \(x^{2}+72=0\) | |
| Aislar el término cuadrático. | \(x^{2}=-72\) |
| Utilice la Propiedad Raíz Cuadrada. | \(x=\pm \sqrt{-72}\) |
| Simplifique el uso de números complejos. | \(x=\pm \sqrt{72} i\) |
| Simplifica lo radical. | \(x=\pm 6 \sqrt{2} i\) |
| Reescribe para mostrar dos soluciones | \(x=6 \sqrt{2} i, x=-6 \sqrt{2} i\) |
|
Consulta las soluciones: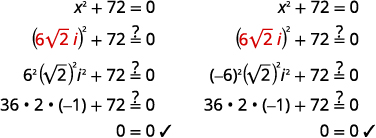 
|
Resolver:\(c^{2}+12=0\).
- Contestar
-
\(c=2 \sqrt{3} i, \quad c=-2 \sqrt{3} i\)
Resolver:\(q^{2}+24=0\).
- Contestar
-
\(c=2 \sqrt{6} i, \quad c=-2 \sqrt{6} i\)
Nuestro método también funciona cuando ocurren fracciones en la ecuación, resolvemos como cualquier ecuación con fracciones. En el siguiente ejemplo, primero aislamos el término cuadrático, y luego hacemos que el coeficiente sea igual a uno.
Resolver:\(\frac{2}{3} u^{2}+5=17\).
Solución:
| \(\frac{2}{3} u^{2}+5=17\) | |
| Aislar el término cuadrático. |  |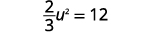
| \(\frac{3}{2}\)Multiplicar por para hacer el coeficiente\(1\). |  |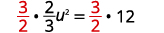
| Simplificar. |  |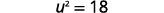
| Utilice la Propiedad Raíz Cuadrada. |  |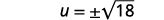
| Simplifica lo radical. |  |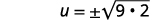
| Simplificar. |  |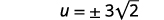
| Reescribe para mostrar dos soluciones. |  |
|
Comprobar: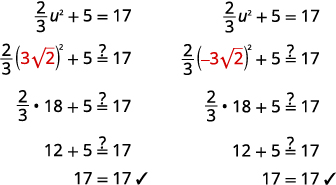 
|
Resolver:\(\frac{1}{2} x^{2}+4=24\).
- Contestar
-
\(x=2 \sqrt{10}, x=-2 \sqrt{10}\)
Resolver:\(\frac{3}{4} y^{2}-3=18\).
- Contestar
-
\(y=2 \sqrt{7}, y=-2 \sqrt{7}\)
Las soluciones a algunas ecuaciones pueden tener fracciones dentro de los radicales. Cuando esto sucede, debemos racionalizar el denominador.
Resolver:\(2 x^{2}-8=41\).
Solución:
 |
|
| Aislar el término cuadrático. |  |
| Dividir por\(2\) para hacer el coeficiente\(1\). |  |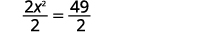
| Simplificar. |  |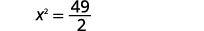
| Utilice la Propiedad Raíz Cuadrada. |  |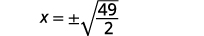
| Reescribir el radical como una fracción de raíces cuadradas. |  |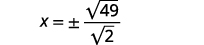
| Racionalizar el denominador. |  |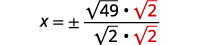
| Simplificar. |  |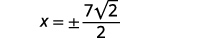
| Reescribe para mostrar dos soluciones. |  |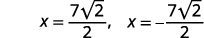
|
Comprobar: Te dejamos chequear por ti. |
Resolver:\(5 r^{2}-2=34\).
- Contestar
-
\(r=\frac{6 \sqrt{5}}{5}, \quad r=-\frac{6 \sqrt{5}}{5}\)
Resolver:\(3 t^{2}+6=70\).
- Contestar
-
\(t=\frac{8 \sqrt{3}}{3}, \quad t=-\frac{8 \sqrt{3}}{3}\)
Resolver Ecuación Cuadrática de la Forma\(a(x-h)^{2}=k\) Usando la Propiedad Raíz Cuadrada
Podemos usar la Propiedad Raíz Cuadrada para resolver una ecuación de la\(a(x-h)^{2}=k\) forma también. Observe que el término cuadrático\(x\),, en la forma original\(ax^{2}=k\) se sustituye por\((x-h)\).
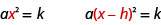
El primer paso, como antes, es aislar el término que tiene la variable al cuadrado. En este caso, se está cuadrando un binomio. Una vez aislado el binomio, dividiendo cada lado por el coeficiente de\(a\), entonces se puede usar la Propiedad Raíz Cuadrada en\((x-h)^{2}\).
Resolver:\(4(y-7)^{2}=48\).
Solución:
| \(4(y-7)^{2}=48\) | |
| Dividir ambos lados por el coeficiente\(4\). | \((y-7)^{2}=12\) |
| Utilice la Propiedad Raíz Cuadrada en el binomio. | \(y-7=\pm \sqrt{12}\) |
| Simplifica lo radical. | \(y-7=\pm 2 \sqrt{3}\) |
| Resolver para\(y\). | \(y=7 \pm 2 \sqrt{3}\) |
| Reescribe para mostrar dos soluciones. | \(y=7+2 \sqrt{3}\) \(y=7-2 \sqrt{3}\) |
|
Comprobar: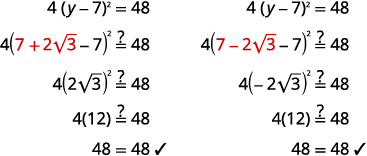 
|
Resolver:\(3(a-3)^{2}=54\).
- Contestar
-
\(a=3+3 \sqrt{2}, \quad a=3-3 \sqrt{2}\)
Resolver:\(2(b+2)^{2}=80\).
- Contestar
-
\(b=-2+2 \sqrt{10}, \quad b=-2-2 \sqrt{10}\)
Recuerda cuando tomamos la raíz cuadrada de una fracción, podemos tomar la raíz cuadrada del numerador y denominador por separado.
Resolver:\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\).
Solución:
\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\)
Utilice la Propiedad Raíz Cuadrada.
\(x-\frac{1}{3}=\pm \sqrt{\frac{5}{9}}\)
Reescribir el radical como una fracción de raíces cuadradas.
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{\sqrt{9}}\)
Simplifica lo radical.
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{3}\)
Resolver para\(x\).
\(x=\frac{1}{3} \pm \frac{\sqrt{5}}{3}\)
Reescribe para mostrar dos soluciones.
\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}, x=\frac{1}{3}-\frac{\sqrt{5}}{3}\)
Comprobar:
Te dejamos el cheque.
Resolver:\(\left(x-\frac{1}{2}\right)^{2}=\frac{5}{4}\).
- Contestar
-
\(x=\frac{1}{2}+\frac{\sqrt{5}}{2}, x=\frac{1}{2}-\frac{\sqrt{5}}{2}\)
Resolver:\(\left(y+\frac{3}{4}\right)^{2}=\frac{7}{16}\).
- Contestar
-
\(y=-\frac{3}{4}+\frac{\sqrt{7}}{4}, y=-\frac{3}{4}-\frac{\sqrt{7}}{4}\)
Comenzaremos la solución al siguiente ejemplo aislando el término binomial.
Resolver:\(2(x-2)^{2}+3=57\).
Solución:
\(2(x-2)^{2}+3=57\)
Restar\(3\) de ambos lados para aislar el término binomial.
\(2(x-2)^{2}=54\)
Divide ambos lados por\(2\).
\((x-2)^{2}=27\)
Utilice la Propiedad Raíz Cuadrada.
\(x-2=\pm \sqrt{27}\)
Simplifica lo radical.
\(x-2=\pm 3 \sqrt{3}\)
Resolver para\(x\).
\(x=2 \pm 3 \sqrt{3}\)
Reescribe para mostrar dos soluciones.
\(x=2+3 \sqrt{3}, x=2-3 \sqrt{3}\)
Comprobar:
Te dejamos el cheque.
Resolver:\(5(a-5)^{2}+4=104\).
- Contestar
-
\(a=5+2 \sqrt{5}, a=5-2 \sqrt{5}\)
Resolver:\(3(b+3)^{2}-8=88\).
- Contestar
-
\(b=-3+4 \sqrt{2}, \quad b=-3-4 \sqrt{2}\)
A veces las soluciones son números complejos.
Resolver:\((2 x-3)^{2}=-12\).
Solución:
\((2 x-3)^{2}=-12\)
Utilice la Propiedad Raíz Cuadrada.
\(2 x-3=\pm \sqrt{-12}\)
Simplifica lo radical.
\(2 x-3=\pm 2 \sqrt{3} i\)
Añadir\(3\) a ambos lados.
\(2 x=3 \pm 2 \sqrt{3} i\)
Divide ambos lados por\(2\).
\(x=\frac{3 \pm 2 \sqrt{3 i}}{2}\)
Reescribir en forma estándar.
\(x=\frac{3}{2} \pm \frac{2 \sqrt{3} i}{2}\)
Simplificar.
\(x=\frac{3}{2} \pm \sqrt{3} i\)
Reescribe para mostrar dos soluciones.
\(x=\frac{3}{2}+\sqrt{3} i, x=\frac{3}{2}-\sqrt{3} i\)
Comprobar:
Te dejamos el cheque.
Resolver:\((3 r+4)^{2}=-8\).
- Contestar
-
\(r=-\frac{4}{3}+\frac{2 \sqrt{2} i}{3}, r=-\frac{4}{3}-\frac{2 \sqrt{2} i}{3}\)
Resolver:\((2 t-8)^{2}=-10\).
- Contestar
-
\(t=4+\frac{\sqrt{10} i}{2}, t=4-\frac{\sqrt{10 i}}{2}\)
Los lados izquierdos de las ecuaciones en los siguientes dos ejemplos no parecen ser de la forma\(a(x-h)^{2}\). Pero son trinomios cuadrados perfectos, así que vamos a factorizarlos para ponerlos en la forma que necesitamos.
Resolver:\(4 n^{2}+4 n+1=16\).
Solución:
Observamos que el lado izquierdo de la ecuación es un trinomio cuadrado perfecto. Lo faccionaremos primero.
| \(4 n^{2}+4 n+1=16\) | |
| Factorizar el trinomio cuadrado perfecto. | \((2 n+1)^{2}=16\) |
| Utilice la Propiedad Raíz Cuadrada. | \(2 n+1=\pm \sqrt{16}\) |
| Simplifica lo radical. | \(2 n+1=\pm 4\) |
| Resolver para\(n\). | \(2 n=-1 \pm 4\) |
| Dividir cada lado por\(2\). | \(\begin{aligned} \frac{2 n}{2} &=\frac{-1 \pm 4}{2} \\ n &=\frac{-1 \pm 4}{2} \end{aligned}\) |
| Reescribe para mostrar dos soluciones. | \(n=\frac{-1+4}{2}, n=\frac{-1-4}{2}\) |
| Simplifica cada ecuación. | \(n=\frac{3}{2}, \quad n=-\frac{5}{2}\) |
|
Comprobar: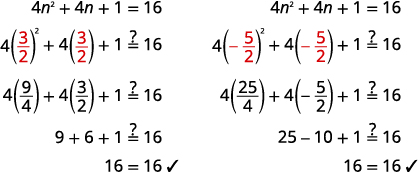 
|
Resolver:\(9 m^{2}-12 m+4=25\).
- Contestar
-
\(m=\frac{7}{3}, \quad m=-1\)
Resolver:\(16 n^{2}+40 n+25=4\).
- Contestar
-
\(n=-\frac{3}{4}, \quad n=-\frac{7}{4}\)
Acceda a este recurso en línea para obtener instrucción adicional y práctica con el uso de la Propiedad Raíz Cuadrada para resolver ecuaciones cuadráticas.
Conceptos clave
- Propiedad Raíz Cuadrada
- Si\(x^{2}=k\), entonces\(x=\sqrt{k}\) o\(x=-\sqrt{k}\) o\(x=\pm \sqrt{k}\)
- Aísle el término cuadrático y haga su coeficiente uno.
- Utilice la Propiedad Raíz Cuadrada.
- Simplifica lo radical.
- Consulta las soluciones.