9.9: Resolver desigualdades cuadráticas

Última actualización
Guardar como PDF

Page ID: 112591

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Resolver las desigualdades cuadráticas gráficamente
Resolver desigualdades cuadráticas algebraicamente

Antes de comenzar, toma este cuestionario de preparación.

Resolver:$2x−3=0$.
Si te perdiste este problema, revisa el Ejemplo 2.2.
Resolver:$2y^{2}+y=15$.
Si te perdiste este problema, revisa el Ejemplo 6.45.
Resolver$\frac{1}{x^{2}+2 x-8}>0$
Si te perdiste este problema, revisa Ejemplo 7.56.

Anteriormente hemos aprendido a resolver desigualdades lineales y racionales. Algunas de las técnicas que utilizamos para resolverlos fueron las mismas y otras diferentes. Ahora aprenderemos a resolver desigualdades que tienen una expresión cuadrática. Utilizaremos algunas de las técnicas de resolución de desigualdades lineales y racionales, así como ecuaciones cuadráticas. Resolveremos las desigualdades cuadráticas de dos maneras, tanto gráfica como algebraicamente.

Resolver las desigualdades cuadráticas gráficamente

Una ecuación cuadrática está en forma estándar cuando se escribe como$ax^{2}+bx+c=0$. Si reemplazamos el signo igual por un signo de desigualdad, tenemos una desigualdad cuadrática en forma estándar.

Definición$\PageIndex{1}$: Quadratic Inequality

Una desigualdad cuadrática es una desigualdad que contiene una expresión cuadrática. La forma estándar de una desigualdad cuadrática está escrita:

$\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}$

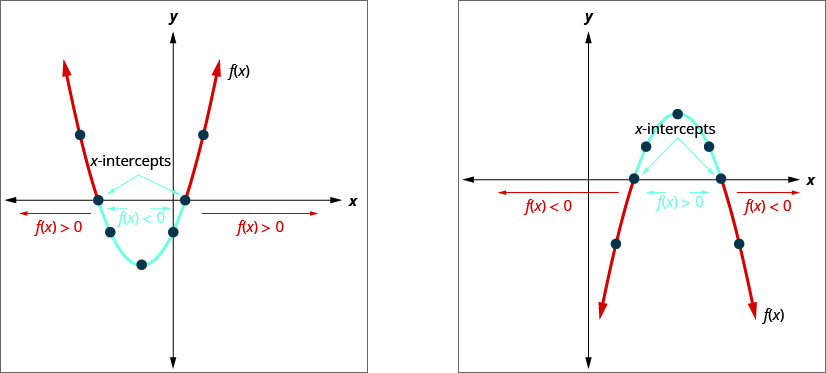
La gráfica de una función cuadrática$f(x)=a x^{2}+b x+c=0$ es una parábola. Cuando preguntamos cuándo es$a x^{2}+b x+c<0$, estamos preguntando cuándo es$f(x)<0$. Queremos saber cuándo la parábola está por debajo del$x$ eje -eje.

Cuando preguntamos cuándo es$a x^{2}+b x+c>0$, estamos preguntando cuándo es$f(x)>0$. Queremos saber cuándo la parábola está por encima del$y$ eje -eje.

La primera gráfica es una parábola orientada hacia arriba, f de x, en un plano de coordenadas x y. A la izquierda de la función, f de x es mayor que 0. Entre las intercepciones x, f de x es menor que 0. A la derecha de la función, f de x es mayor que 0. La segunda gráfica es una parábola orientada hacia abajo, f de x, en un plano de coordenadas x y. A la izquierda de la función, f de x es menor que 0. Entre las intercepciones x, f de x es mayor que 0. A la derecha de la función, f de x es menor que 0. — Figura 9.8.1

Ejemplo$\PageIndex{1}$: How to Solve a Quadratic Inequality Graphically

Resuelve$x^{2}−6x+8<0$ gráficamente. Escribe la solución en notación de intervalos.

Solución:

Paso 1: Escribir la desigualdad cuadrática en forma estándar.

La desigualdad está en forma estándar.

$x^{2}-6 x+8<0$

Paso 2: Grafica la función$f(x)=a x^{2}+b x+c$ usando propiedades o transformaciones.

Vamos a graficar usando las propiedades.

$f(x)=x^{2}-6 x+8$

Mirar$a$ en la ecuación.

$\color{red}{a=1, b=-6, c=8}$

$f(x)=x^{2}-6 x+8$

Como$a$ es positivo, la parábola se abre hacia arriba.

La parábola se abre hacia arriba.

Captura de pantalla (2) .png — Figura 9.8.2

$f(x)=x^{2}-6 x+8$

El eje de simetría es la línea$x=-\frac{b}{2 a}$.

Eje de simetría

$x=-\frac{b}{2 a}$

$\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}$

El eje de simetría es la línea$x=3$.

El vértice está en el eje de simetría. Sustituir$x=3$ a la función.

Vertex

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}$

El vértice es$(3,-1)$.

ENCONTRAMOS$f(0)$

$y$-interceptar

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}$

El$y$ -intercepto es$(0.8)$.

Utilizamos el eje de simetría para encontrar un punto simétrico a la$y$ intersección. El$y$ -intercepto es$3$ unidades a la izquierda del eje de simetría,$x=3$. A$3$ unidades de punto a la derecha del eje de simetría tiene$x=6$.

Punto simétrico a$y$ -intercepción

El punto es$(6,8)$.

Resolvemos$f(x)=0$.

$x$-intercepta

Podemos resolver esta ecuación cuadrática factorizando.

$\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}$

Los$x$ -interceptos son$(2,0)$ y$(4,0)$.

Gráficamos el vértice, las intercepciones y el punto simétrico a la$y$ intersección. Conectamos estos$5$ puntos para bosquejar la parábola.

Captura de pantalla (3) .png — Figura 9.8.3

Paso 3: Determine la solución a partir de la gráfica.

$x^{2}-6 x+8<0$

La desigualdad pide los valores de los$x$ cuales hacen que la función sea menor que$0$. Que valores de$x$ hacen la parábola por debajo del$x$ eje -.

No incluimos los valores$2$,$4$ ya que la desigualdad es menor que solo.

La solución, en notación de intervalos, es$(2,4)$.

Ejercicio$\PageIndex{1}$

Resolver$x^{2}+2 x-8<0$ gráficamente
Escribir la solución en notación de intervalos

Contestar

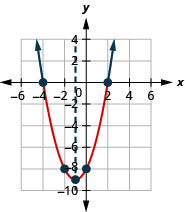
$Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 2, negativo 9), y intercepción de (0, 8), y eje de simetría mostrado en x es igual a negativo 2.$
Figura 9.8.4
$(-4,2)$

Ejercicio$\PageIndex{2}$

Resolver$x^{2}-8 x+12 \geq 0$ gráficamente
Escribir la solución en notación de intervalos

Contestar

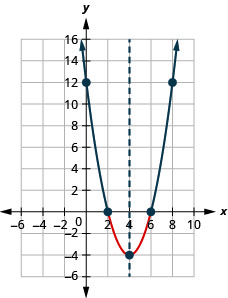
$Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (4, negativo 4) e intercepciones x de (2, 0) y (6, 0).$
Figura 9.8.5
$(-\infty, 2] \cup[6, \infty)$

Enumeramos los pasos a seguir para resolver gráficamente una desigualdad cuadrática.

Resolver una desigualdad cuadrática gráficamente

Escribir la desigualdad cuadrática en forma estándar.
Grafica la función$f(x)=ax^{2}+bx+c$.
Determine la solución a partir de la gráfica.

En el último ejemplo, la parábola se abrió hacia arriba y en el siguiente ejemplo, se abre hacia abajo. En ambos casos, estamos buscando la parte de la parábola que está por debajo del$x$ eje -pero note cómo la posición de la parábola afecta a la solución.

Ejemplo$\PageIndex{2}$

Resuelve$-x^{2}-8 x-12 \leq 0$ gráficamente. Escribe la solución en notación de intervalos.

Solución:

Cuadro 9.8.1
La desigualdad cuadrática en forma estándar.	$-x^{2}-8 x-12 \leq 0$
Graficar la función $f(x)=-x^{2}-8 x-12$	La parábola se abre hacia abajo. $.$ Figura 9.8.6
Encuentra la línea de simetría.	$\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}$
Encuentra el vértice.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}$ Vértice$(-4,4)$
Encuentra las$x$ -intercepciones. Vamos$f(x)=0$.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}$
Factor: Utilice la Propiedad de Producto Cero.	$\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}$
Grafica la parábola.	$x$-intercepta$(-6,0), (-2.0)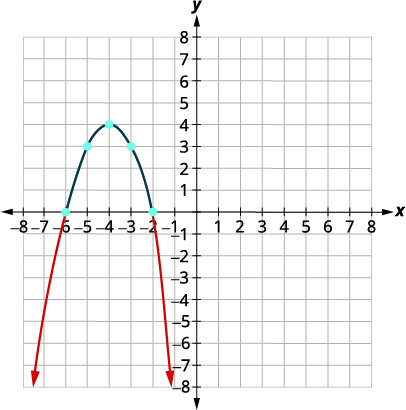$ $.$ Figura 9.8.7
Determine la solución a partir de la gráfica. Incluimos los$x$ -interceptos ya que la desigualdad es “menor o igual a”.	$(-\infty,-6] \cup[-2, \infty)$

Ejercicio$\PageIndex{3}$

Resolver$-x^{2}-6 x-5>0$ gráficamente
Escribir la solución en notación de intervalos

Contestar

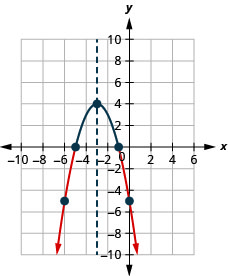
$Parábola orientada hacia abajo en el plano de coordenadas x y. Tiene un vértice de (negativo 3, 4), una intercepción y en (0, negativo 5), y un eje de simetría mostrado en x es igual a negativo 3.$
Figura 9.8.8
$(-5,-1)$

Ejercicio$\PageIndex{4}$

Resolver$−x^{2}+10x−16≤0$ gráficamente
Escribir la solución en notación de intervalos

Contestar

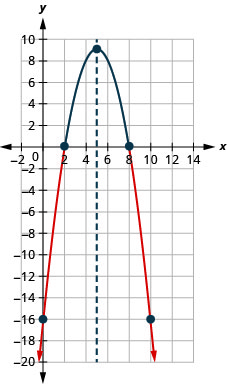
$Parábola orientada hacia abajo en el plano de coordenadas x y. Tiene un vértice de (5, 9), una intercepción y en (0, 16 negativo), y un eje de simetría de x es igual a 5.$
Figura 9.8.9
$(-\infty, 2] \cup[8, \infty)$

Resolver desigualdades cuadráticas algebraicamente

El método algebraico que usaremos es muy similar al método que usamos para resolver desigualdades racionales. Encontraremos los puntos críticos para la desigualdad, que serán las soluciones a la ecuación cuadrática relacionada. Recuerde que una expresión polinómica puede cambiar signos solo donde la expresión es cero.

Utilizaremos los puntos críticos para dividir la recta numérica en intervalos y luego determinar si la expresión cuadrática será positiva o negativa en el intervalo. Luego determinamos la solución a la desigualdad.

Ejemplo$\PageIndex{3}$: How to Solve Quadratic Inequalities Algebraically

Resolver$x^{2}-x-12 \geq 0$ algebraicamente. Escribe la solución en notación de intervalos.

Solución:

Cuadro 9.8.2
Paso 1: Escribir la desigualdad cuadrática en forma estándar.	La desigualdad está en forma estándar.	$x^{2}-x-12 \geq 0$
Paso 2: Determinar los puntos críticos, las soluciones a la ecuación cuadrática relacionada.	Cambiar el signo de desigualdad por un signo igual y luego resolver la ecuación.	$\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}$
Paso 3: Utilice los puntos críticos para dividir la línea numérica en intervalos.	Utilizar$-3$ y$4$ dividir la recta numérica en intervalos.	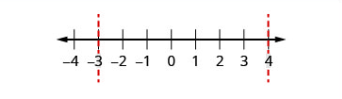$Captura de pantalla (4) .png$
Paso 4: Por encima de la recta numérica se muestra el signo de cada expresión cuadrática utilizando puntos de prueba de cada intervalo sustituidos de la desigualdad original.	Prueba: $x=-5$ $x=0$ $x=5$	$\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}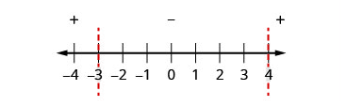$ $Captura de pantalla (5) .png$ Figura 9.8.11
Paso 5: Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.	$x^{2}-x-12 \geq 0$ La desigualdad es positiva en los intervalos primero y último e igual$0$ en los puntos$-4,3$.	La solución, en notación de intervalos, es$(-\infty,-3] \cup[4, \infty)$.

Ejercicio$\PageIndex{5}$

Resolver$x^{2}+2x−8≥0$ algebraicamente. Escribe la solución en notación de intervalos.

Contestar: $(-\infty,-4] \cup[2, \infty)$

Ejercicio$\PageIndex{6}$

Resolver$x^{2}−2x−15≤0$ algebraicamente. Escribe la solución en notación de intervalos.

Contestar: $[-3,5]$

En este ejemplo, dado que los$x^{2}−x−12$ factores de expresión muy bien, también podemos encontrar el signo en cada intervalo como lo hicimos cuando resolvimos desigualdades racionales. Encontramos el signo de cada uno de los factores, y luego el signo del producto. A nuestra línea numérica le gustaría esto:

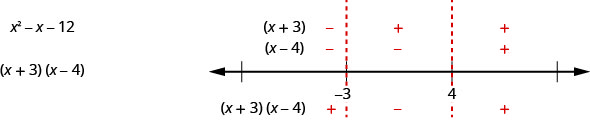
La figura muestra la expresión x cuadrado menos x menos 12 factorizada a la cantidad de x más 3 veces la cantidad de x menos 4. La imagen muestra una línea numérica que muestra líneas punteadas en negativo 3 y 4. Muestra los signos de la cantidad x más 3 para ser negativos, positivos, positivos, y los signos de la cantidad x menos 4 para ser negativos, negativos, positivos. Debajo de la recta numérica, se muestra la cantidad x más 3 veces la cantidad x menos 4 con los signos positivo, negativo, positivo. — Figura 9.8.12

El resultado es el mismo que encontramos usando el otro método.

Resumimos los pasos aquí.

Resolver una desigualdad cuadrática algebraicamente

Escribir la desigualdad cuadrática en forma estándar.
Determinar los puntos críticos: las soluciones a la ecuación cuadrática relacionada.
Utilice los puntos críticos para dividir la recta numérica en intervalos.
Por encima de la recta numérica se muestra el signo de cada expresión cuadrática utilizando puntos de prueba de cada intervalo sustituido a la desigualdad original.
Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.

Ejemplo$\PageIndex{4}$

Resolver$x^{2}+6x−7≥0$ algebraicamente. Escribe la solución en notación de intervalos.

Solución:

Cuadro 9.8.3
Escribir la desigualdad cuadrática en forma estándar.	$-x^{2}+6 x-7 \geq 0$
Multiplicar ambos lados de la desigualdad por$-1$. Recuerda revertir el signo de desigualdad.	$x^{2}-6 x+7 \leq 0$
Determinar los puntos críticos resolviendo la ecuación cuadrática relacionada.	$x^{2}-6 x+7=0$
Escribe la Fórmula Cuadrática.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Después sustituya en los valores de$a, b, c$.	$x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}$
Simplificar.	$x=\frac{6 \pm \sqrt{8}}{2}$
Simplifica lo radical.	$x=\frac{6 \pm 2 \sqrt{2}}{2}$
Eliminar el factor común,$2$.	$\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}$
Utilice los puntos críticos para dividir la recta numérica en intervalos. Pruebe los números de cada intervalo en la desigualdad original.	$.$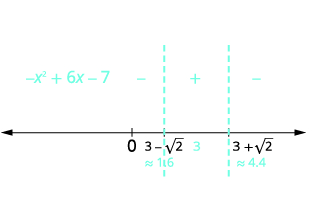
Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.	$-x^{2}+6 x-7 \geq 0$en el intervalo medio$[3-\sqrt{2}, 3+\sqrt{2}]$

Ejercicio$\PageIndex{7}$

Resolver$−x^{2}+2x+1≥0$ algebraicamente. Escribe la solución en notación de intervalos.

Contestar: $[-1-\sqrt{2},-1+\sqrt{2}]$

Ejercicio$\PageIndex{8}$

Resolver$−x^{2}+8x−14<0$ algebraicamente. Escribe la solución en notación de intervalos.

Contestar: $(-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)$

Las soluciones de las desigualdades cuadráticas en cada uno de los ejemplos anteriores, fueron o bien un intervalo o la unión de dos intervalos. Esto resultó de que, en cada caso encontramos dos soluciones a la ecuación cuadrática correspondiente$ax^{2}+bx+c=0$. Estas dos soluciones nos dieron entonces ya sea las dos$x$ - intercepciones para la gráfica o los dos puntos críticos para dividir la recta numérica en intervalos.

Esto se correlaciona con nuestra discusión previa del número y tipo de soluciones a una ecuación cuadrática usando el discriminante.

Para una ecuación cuadrática de la forma$ax^{2}+bc+c=0, a≠0$.

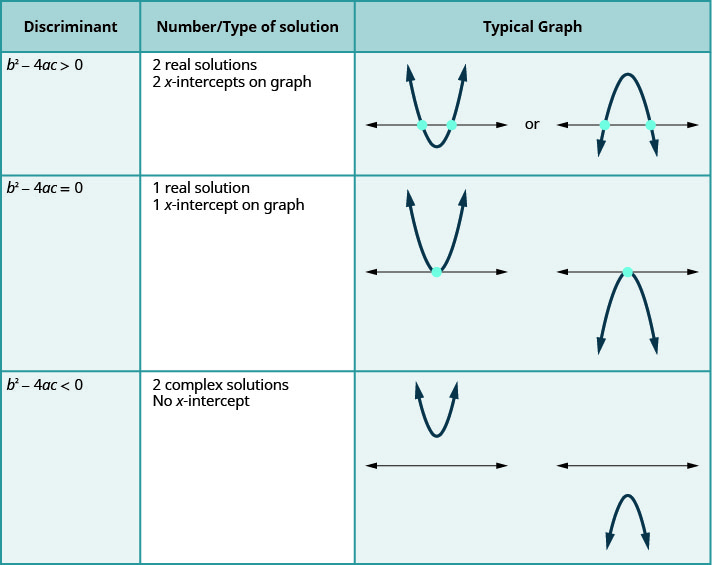
La figura es una tabla con 3 columnas. La columna 1 está etiquetada como discriminante, la columna 2 es Número/Tipo de solución y la columna 3 es Gráfica Típica. Al leer a través de las columnas, si b al cuadrado menos 4 veces por c es mayor que 0, habrá 2 soluciones reales porque hay 2 intercepciones x en la gráfica. La imagen de una gráfica típica una parábola ascendente o descendente con 2 intercepciones x. Si el discriminante b al cuadrado menos 4 veces a veces c es igual a 0, entonces hay 1 solución real porque hay 1 intercepción x en la gráfica. La imagen de la gráfica típica es una parábola orientada hacia arriba o hacia abajo que tiene un vértice en el eje x en lugar de cruzarlo. Si el discriminante b al cuadrado menos 4 veces a veces c es menor que 0, hay 2 soluciones complejas porque no hay intercepción x. La imagen de la gráfica típica muestra una parábola orientada hacia arriba o hacia abajo que no cruza el eje x. — Figura 9.8.14

La última fila de la tabla nos muestra cuando las parábolas nunca se cruzan con el$x$ eje. Usando la Fórmula Cuadrática para resolver la ecuación cuadrática, el radicando es negativo. Obtenemos dos soluciones complejas.

En el siguiente ejemplo, las soluciones de desigualdad cuadrática resultarán de que la solución de la ecuación cuadrática sea compleja.

Ejemplo$\PageIndex{5}$

Resuelve, escribiendo cualquier solución en notación de intervalos:

$x^{2}-3 x+4>0$
$x^{2}-3 x+4 \leq 0$

Solución:

Cuadro 9.8.4
Escribir la desigualdad cuadrática en forma estándar.	$-x^{2}-3 x+4>0$
Determinar los puntos críticos resolviendo la ecuación cuadrática relacionada.	$x^{2}-3 x+4=0$
Escribe la Fórmula Cuadrática.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Después sustituya en los valores de$a, b, c$.	$x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}$
Simplificar.	$x=\frac{3 \pm \sqrt{-7}}{2}$
Simplifica el radicando.	$x=\frac{3 \pm \sqrt{7 i}}{2}$
Las soluciones complejas nos dicen que la parábola no intercepta el$x$ eje -eje. También, la parábola se abre hacia arriba. Esto nos dice que la parábola está completamente por encima del$x$ eje -eje.	Soluciones complejas 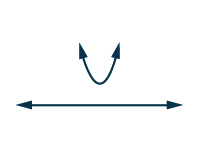$.$ Figura 9.8.15

Estamos para encontrar la solución a$x^{2}−3x+4>0$. Ya que para todos los valores de$x$ la gráfica está por encima del$x$ eje -, todos los valores de$x$ hacen que la desigualdad sea verdadera. En notación de intervalos escribimos$(−∞,∞)$.

b. Escribir la desigualdad cuadrática en forma estándar.

$x^{2}-3 x+4 \leq 0$

Determinar los puntos críticos resolviendo la ecuación cuadrática relacionada.

$x^{2}-3 x+4=0$

Dado que la ecuación cuadrática correspondiente es la misma que en la parte (a), la parábola será la misma. La parábola se abre hacia arriba y está completamente por encima del$x$ eje -no hay parte de ella por debajo del$x$ eje-.

Estamos para encontrar la solución a$x^{2}−3x+4≤0$. Ya que para todos los valores de$x$ la gráfica nunca se encuentra por debajo del$x$ eje -, ningún valor de$x$ hacer verdadera la desigualdad. No hay solución a la desigualdad.

Ejercicio$\PageIndex{9}$

Resuelve y escribe cualquier solución en notación de intervalos:

$-x^{2}+2 x-4 \leq 0$
$-x^{2}+2 x-4 \geq 0$

Contestar

$(-\infty, \infty)$
no hay solución

Ejercicio$\PageIndex{10}$

Resuelve y escribe cualquier solución en notación de intervalos:

$x^{2}+3 x+3<0$
$x^{2}+3 x+3>0$

Contestar

no hay solución
$(-\infty, \infty)$

Conceptos clave

Resolver una desigualdad cuadrática gráficamente
1. Escribir la desigualdad cuadrática en forma estándar.
2. Grafica la función$f(x)=ax^{2}+bx+c$ usando propiedades o transformaciones.
3. Determine la solución a partir de la gráfica.
Cómo Resolver una Desigualdad Cuadrática Algebraicamente
1. Escribir la desigualdad cuadrática en forma estándar.
2. Determinar los puntos críticos — las soluciones a la ecuación cuadrática relacionada.
3. Utilice los puntos críticos para dividir la recta numérica en intervalos.
4. Por encima de la recta numérica se muestra el signo de cada expresión cuadrática utilizando puntos de prueba de cada intervalo sustituido a la desigualdad original.
5. Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.

Glosario

desigualdad cuadrática: Una desigualdad cuadrática es una desigualdad que contiene una expresión cuadrática.

La desigualdad cuadrática en forma estándar.	\(-x^{2}-8 x-12 \leq 0\)
Graficar la función \(f(x)=-x^{2}-8 x-12\)	La parábola se abre hacia abajo. $.$ Figura 9.8.6
Encuentra la línea de simetría.	\(\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}\)
Encuentra el vértice.	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}\) Vértice\((-4,4)\)
Encuentra las\(x\) -intercepciones. Vamos\(f(x)=0\).	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}\)
Factor: Utilice la Propiedad de Producto Cero.	\(\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}\)
Grafica la parábola.	\(x\)-intercepta\((-6,0), (-2.0)\) $.$ Figura 9.8.7
Determine la solución a partir de la gráfica. Incluimos los\(x\) -interceptos ya que la desigualdad es “menor o igual a”.	\((-\infty,-6] \cup[-2, \infty)\)

Escribir la desigualdad cuadrática en forma estándar.	\(-x^{2}+6 x-7 \geq 0\)
Multiplicar ambos lados de la desigualdad por\(-1\). Recuerda revertir el signo de desigualdad.	\(x^{2}-6 x+7 \leq 0\)
Determinar los puntos críticos resolviendo la ecuación cuadrática relacionada.	\(x^{2}-6 x+7=0\)
Escribe la Fórmula Cuadrática.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Después sustituya en los valores de\(a, b, c\).	\(x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}\)
Simplificar.	\(x=\frac{6 \pm \sqrt{8}}{2}\)
Simplifica lo radical.	\(x=\frac{6 \pm 2 \sqrt{2}}{2}\)
Eliminar el factor común,\(2\).	\(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}\)
Utilice los puntos críticos para dividir la recta numérica en intervalos. Pruebe los números de cada intervalo en la desigualdad original.	$.$
Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.	\(-x^{2}+6 x-7 \geq 0\)en el intervalo medio\([3-\sqrt{2}, 3+\sqrt{2}]\)

Escribir la desigualdad cuadrática en forma estándar.	\(-x^{2}-3 x+4>0\)
Determinar los puntos críticos resolviendo la ecuación cuadrática relacionada.	\(x^{2}-3 x+4=0\)
Escribe la Fórmula Cuadrática.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Después sustituya en los valores de\(a, b, c\).	\(x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}\)
Simplificar.	\(x=\frac{3 \pm \sqrt{-7}}{2}\)
Simplifica el radicando.	\(x=\frac{3 \pm \sqrt{7 i}}{2}\)
Las soluciones complejas nos dicen que la parábola no intercepta el\(x\) eje -eje. También, la parábola se abre hacia arriba. Esto nos dice que la parábola está completamente por encima del\(x\) eje -eje.	Soluciones complejas $.$ Figura 9.8.15

Search

Text Color

Text Size

Margin Size

Font Type

Definición\(\PageIndex{1}\): Quadratic Inequality

Ejemplo\(\PageIndex{1}\): How to Solve a Quadratic Inequality Graphically

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejemplo\(\PageIndex{3}\): How to Solve Quadratic Inequalities Algebraically

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejemplo\(\PageIndex{4}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejemplo\(\PageIndex{5}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Paso 1: Escribir la desigualdad cuadrática en forma estándar.	La desigualdad está en forma estándar.	\(x^{2}-x-12 \geq 0\)
Paso 2: Determinar los puntos críticos, las soluciones a la ecuación cuadrática relacionada.	Cambiar el signo de desigualdad por un signo igual y luego resolver la ecuación.	\(\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}\)
Paso 3: Utilice los puntos críticos para dividir la línea numérica en intervalos.	Utilizar\(-3\) y\(4\) dividir la recta numérica en intervalos.	$Captura de pantalla (4) .png$
Paso 4: Por encima de la recta numérica se muestra el signo de cada expresión cuadrática utilizando puntos de prueba de cada intervalo sustituidos de la desigualdad original.	Prueba: \(x=-5\) \(x=0\) \(x=5\)	\(\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}\) $Captura de pantalla (5) .png$ Figura 9.8.11
Paso 5: Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.	\(x^{2}-x-12 \geq 0\) La desigualdad es positiva en los intervalos primero y último e igual\(0\) en los puntos\(-4,3\).	La solución, en notación de intervalos, es\((-\infty,-3] \cup[4, \infty)\).