Saltar al contenido principal
LibreTexts Español

9.8E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112639

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    Ejercicio\(\PageIndex{23}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}=k\)

    En los siguientes ejercicios,

    1. Graficar las funciones cuadráticas en el mismo sistema de coordenadas rectangulares
    2. Describir qué efecto tiene la adición de una constante\(k\),, a la función sobre la parábola básica.
      1. \(f(x)=x^{2}, g(x)=x^{2}+4, \text { and } h(x)=x^{2}-4\)
      2. \(f(x)=x^{2}, g(x)=x^{2}+7, \text { and } h(x)=x^{2}-7\)
    Contestar

    1.


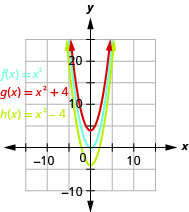
    1. Esta figura muestra 3 parábola de apertura hacia arriba en el plano de la coordenada x y. La curva media es la gráfica de f de x es igual a x cuadrado y tiene un vértice de (0, 0). Otros puntos de la curva se ubican en (negativo 1, 1) y (1, 1). La curva superior se ha movido hacia arriba 4 unidades, y la parte inferior se ha movido hacia abajo 4 unidades.
      Figura 9.7.71
    2. La gráfica de\(g(x)=x^{2}+4\) es la misma que la gráfica de\(4\) unidades\(f(x)=x^{2}\) pero desplazada hacia arriba. La gráfica de\(h(x)=x^{2}-4\) es la misma que la gráfica de\(f(x)=x^{2}\) pero desplazan hacia abajo\(4\) unidades.
    Ejercicio\(\PageIndex{24}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}=k\)

    En los siguientes ejercicios, grafica cada función usando un desplazamiento vertical.

    1. \(f(x)=x^{2}+3\)
    2. \(f(x)=x^{2}-7\)
    3. \(g(x)=x^{2}+2\)
    4. \(g(x)=x^{2}+5\)
    5. \(h(x)=x^{2}-4\)
    6. \(h(x)=x^{2}-5\)
    Contestar

    1.

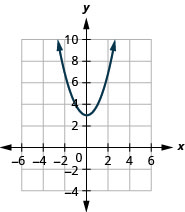
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (0, 3) y otros puntos (7, 2) y (7, negativo 2).
    Figura 9.7.72

    3.

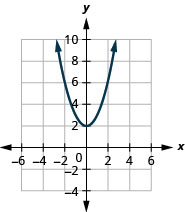
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (0, 2) y otros puntos (negativos 2, 6) y (2, 6).
    Figura 9.7.73

    5.

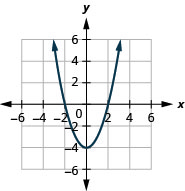
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (0, negativo 4) y otros puntos (negativo 2, 0) y (2, 0).
    Figura 9.7.74
    Ejercicio\(\PageIndex{25}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    En los siguientes ejercicios,

    1. Graficar las funciones cuadráticas en el mismo sistema de coordenadas rectangulares
    2. Describir qué efecto tiene la adición de una constante\(h\),, dentro de los paréntesis
      1. \(f(x)=x^{2}, g(x)=(x-3)^{2}, \text { and } h(x)=(x+3)^{2}\)
      2. \(f(x)=x^{2}, g(x)=(x+4)^{2}, \text { and } h(x)=(x-4)^{2}\)
    Contestar

    1.


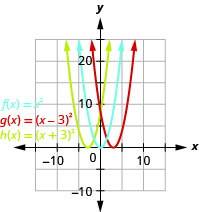
    1. Esta figura muestra 3 parábola de apertura hacia arriba en el plano de la coordenada x y. Una es la gráfica de f de x es igual a x al cuadrado y tiene un vértice de (0, 0). Otros puntos de la curva se ubican en (negativo 1, 1) y (1, 1). La gráfica de la derecha se desplaza 3 unidades a la derecha para producir g de x es igual a la cantidad de x menos 3 al cuadrado. La gráfica de la izquierda se desplaza 3 unidades a la izquierda para producir h de x es igual a la cantidad de x más 3 al cuadrado.
      Figura 9.7.75
    2. La gráfica de\(g(x)=(x−3)^{2}\) es la misma que la gráfica de\(3\) unidades\(f(x)=x^{2}\) pero desplazadas a la derecha. La gráfica de\(h(x)=(x+3)^{2}\) es la misma que la gráfica de\(3\) unidades\(f(x)=x^{2}\) pero desplazada a la izquierda.
    Ejercicio\(\PageIndex{26}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    En los siguientes ejercicios, grafica cada función usando un desplazamiento horizontal.

    1. \(f(x)=(x-2)^{2}\)
    2. \(f(x)=(x-1)^{2}\)
    3. \(f(x)=(x+5)^{2}\)
    4. \(f(x)=(x+3)^{2}\)
    5. \(f(x)=(x-5)^{2}\)
    6. \(f(x)=(x+2)^{2}\)
    Contestar

    1.

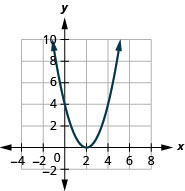
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (2, 0) y otros puntos (0, 4) y (4, 4).
    Figura 9.7.76

    3.

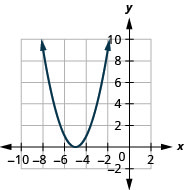
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 5, 0) y otros puntos (negativo 7, 4) y (negativo 3, 4).
    Figura 9.7.77

    5.

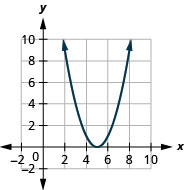
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (5, 0) y otros puntos (3, 4) y (7, 4).
    Figura 9.7.78
    Ejercicio\(\PageIndex{27}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    En los siguientes ejercicios, grafica cada función usando transformaciones.

    1. \(f(x)=(x+2)^{2}+1\)
    2. \(f(x)=(x+4)^{2}+2\)
    3. \(f(x)=(x-1)^{2}+5\)
    4. \(f(x)=(x-3)^{2}+4\)
    5. \(f(x)=(x+3)^{2}-1\)
    6. \(f(x)=(x+5)^{2}-2\)
    7. \(f(x)=(x-4)^{2}-3\)
    8. \(f(x)=(x-6)^{2}-2\)
    Contestar

    1.

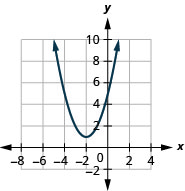
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 2, 1) y otros puntos (negativo 4, 5) y (0, 5).
    Figura 9.7.79

    3.

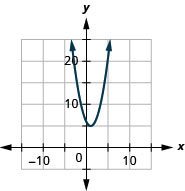
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (1, 5) y otros puntos (negativos 1, 9) y (3, 9).
    Figura 9.7.80

    5.

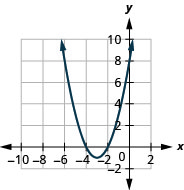
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 3, 1) y otros puntos (negativo 4, 0) y (negativo 2, 0).
    Figura 9.7.81

    7.

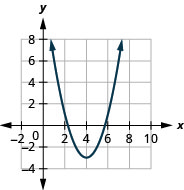
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (4, negativo 2) y otros puntos (3, negativo 2) y (5, negativo 2).
    Figura 9.7.82
    Ejercicio\(\PageIndex{28}\) Graph Quadratic Functions of the Form \(f(x)=ax^{2}\)

    En los siguientes ejercicios, grafica cada función.

    1. \(f(x)=-2 x^{2}\)
    2. \(f(x)=4 x^{2}\)
    3. \(f(x)=-4 x^{2}\)
    4. \(f(x)=-x^{2}\)
    5. \(f(x)=\frac{1}{2} x^{2}\)
    6. \(f(x)=\frac{1}{3} x^{2}\)
    7. \(f(x)=\frac{1}{4} x^{2}\)
    8. \(f(x)=-\frac{1}{2} x^{2}\)
    Contestar

    1.

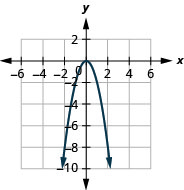
    Esta figura muestra una parábola de apertura hacia abajo en el plano de la coordenada x y. Tiene un vértice de (0, 0) y otros puntos (negativo 1, negativo 2) y (1, negativo 2).
    Figura 9.7.83

    3.

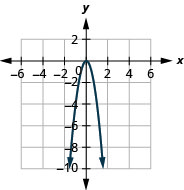
    Esta figura muestra una parábola de apertura hacia abajo en el plano de la coordenada x y. Tiene un vértice de (0, 0) y otros puntos (negativo 1, negativo 4) y (1, negativo 4).
    Figura 9.7.84

    5.

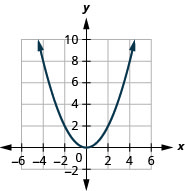
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (0, 0) y otros puntos (negativo 2, 2) y (2, 2).
    Figura 9.7.85

    7.

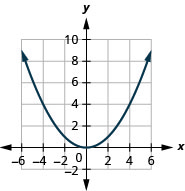
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (0, 0) y otros puntos (2, 1) y (negativo 2, 1).
    Figura 9.7.86
    Ejercicio\(\PageIndex{29}\) Graph Quadratic Functions Using Transformations

    En los siguientes ejercicios, reescribe cada función en el\(f(x)=a(x−h)^{2}+k\) formulario completando el cuadrado.

    1. \(f(x)=-3 x^{2}-12 x-5\)
    2. \(f(x)=2 x^{2}-12 x+7\)
    3. \(f(x)=3 x^{2}+6 x-1\)
    4. \(f(x)=-4 x^{2}-16 x-9\)
    Contestar

    1. \(f(x)=-3(x+2)^{2}+7\)

    3. \(f(x)=3(x+1)^{2}-4\)

    Ejercicio\(\PageIndex{30}\) Graph Quadratic Functions Using Transformations

    En los siguientes ejercicios,

    1. Reescribir cada función en\(f(x)=a(x−h)^{2}+k\) forma
    2. Gráficalo usando transformaciones
      1. \(f(x)=x^{2}+6 x+5\)
      2. \((x)=x^{2}+4 x-12\)
      3. \(f(x)=x^{2}+4 x-12\)
      4. \(f(x)=x^{2}-6 x+8\)
      5. \(f(x)=x^{2}-6 x+15\)
      6. \(f(x)=x^{2}+8 x+10\)
      7. \(f(x)=-x^{2}+8 x-16\)
      8. \(f(x)=-x^{2}+2 x-7\)
      9. \(f(x)=-x^{2}-4 x+2\)
      10. \(f(x)=-x^{2}+4 x-5\)
      11. \(f(x)=5 x^{2}-10 x+8\)
      12. \(f(x)=3 x^{2}+18 x+20\)
      13. \(f(x)=2 x^{2}-4 x+1\)
      14. \(f(x)=3 x^{2}-6 x-1\)
      15. \(f(x)=-2 x^{2}+8 x-10\)
      16. \(f(x)=-3 x^{2}+6 x+1\)
    Contestar

    1.

    1. f (x) = (x+3) ^ {2} -4
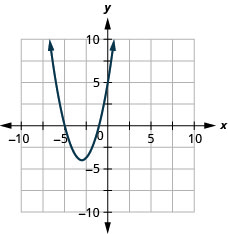
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 3, 3), intercepción y de (0, 5), y eje de simetría mostrado en x es igual a negativo 3.
    Figura 9.7.87

    3.

    1. \(f(x)=(x+2)^{2}-1\)
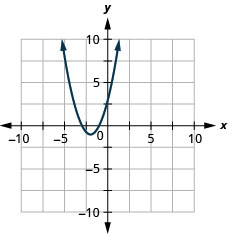
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 2, negativo 1), y intercepción de (0, 3), y eje de simetría mostrado en x es igual a negativo 2.
    Figura 9.7.88

    5.

    1. \(f(x)=(x-3)^{2}+6\)
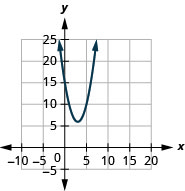
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (3, 6), intercepción y de (0, 10), y eje de simetría mostrado en x es igual a 3.
    Figura 9.7.89

    7.

    1. \(f(x)=-(x-4)^{2}+0\)
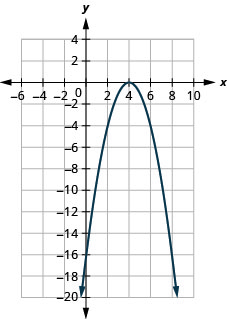
    Esta figura muestra una parábola de apertura hacia abajo en el plano de la coordenada x y. Tiene un vértice de (4, 0), y intercepción de (0, negativo 16), y eje de simetría mostrado en x es igual a 4.
    Figura 9.7.90

    9.

    1. \(f(x)=-(x+2)^{2}+6\)
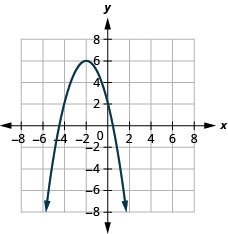
    Esta figura muestra una parábola de apertura hacia abajo en el plano de la coordenada x y. Tiene un vértice de (negativo 2, 6), intercepción y de (0, 2), y eje de simetría mostrado en x es igual a negativo 2.
    Figura 9.7.91

    11.

    1. \(f(x)=5(x-1)^{2}+3\)
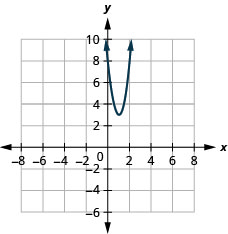
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (1, 3), intercepción y de (0, 8), y eje de simetría mostrado en x es igual a 1.
    Figura 9.7.92

    13.

    1. \(f(x)=2(x-1)^{2}-1\)
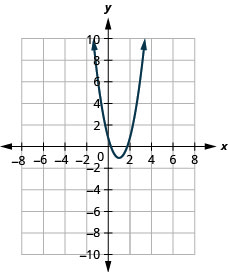
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (1, negativo 1), intercepción y de (0, 1), y eje de simetría mostrado en x es igual a 1.
    Figura 9.7.93

    15.

    1. \(f(x)=-2(x-2)^{2}-2\)
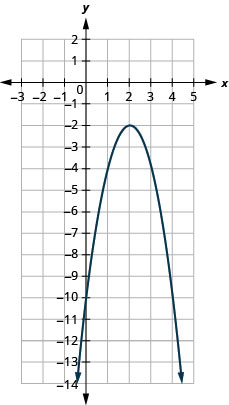
    Esta figura muestra una parábola de apertura hacia abajo en el plano de la coordenada x y. Tiene un vértice de (2, negativo 2), intercepción y de (0, negativo 10), y eje de simetría mostrado en x es igual a 2.
    Figura 9.7.94
    Ejercicio\(\PageIndex{31}\) Graph Quadratic Functions Using Transformations

    En los siguientes ejercicios,

    1. Reescribir cada función en\(f(x)=a(x−h)^{2}+k\) forma
    2. Gráficalo usando propiedades
      1. \(f(x)=2 x^{2}+4 x+6\)
      2. \(f(x)=3 x^{2}-12 x+7\)
      3. \(f(x)=-x^{2}+2 x-4\)
      4. \(f(x)=-2 x^{2}-4 x-5\)
    Contestar

    1.

    1. \(f(x)=2(x+1)^{2}+4\)
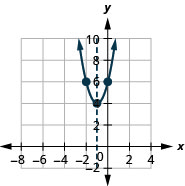
    Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 1, 4), intercepción y de (0, 6), y eje de simetría mostrado en x es igual a negativo 1.
    Figura 9.7.95

    3.

    1. \(f(x)=-(x-1)^{2}-3\)
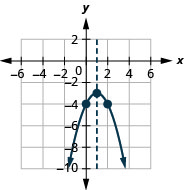
    Esta figura muestra una parábola de apertura hacia abajo en el plano de la coordenada x y. Tiene un vértice de (1, negativo 3), intercepción y de (0, negativo 4), y eje de simetría mostrado en x es igual a 1.
    Figura 9.7.96
    Ejercicio\(\PageIndex{32}\) Matching

    En los siguientes ejercicios, haga coincidir las gráficas con una de las siguientes funciones:

    1. \(f(x)=x^{2}+4\)
    2. \(f(x)=x^{2}-4\)
    3. \(f(x)=(x+4)^{2}\)
    4. \(f(x)=(x-4)^{2}\)
    5. \(f(x)=(x+4)^{2}-4\)
    6. \(f(x)=(x+4)^{2}+4\)
    7. \(f(x)=(x-4)^{2}-4\)
    8. \(f(x)=(x-4)^{2}+4\)

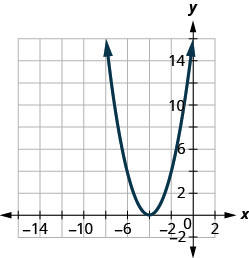
      1. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 4, 0) y otros puntos (negativo 4, 4) y (negativo 2, 4).
        Figura 9.7.97

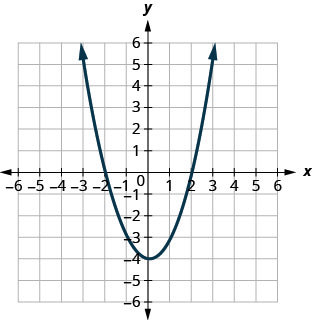
      2. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (0, negativo 4) y otros puntos (negativo 2, 0) y (2, 0).
        Figura 9.7.98

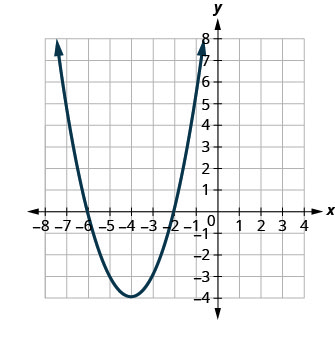
      3. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 4, negativo 4) y otros puntos (negativo 4, 0) y (negativo 2, 0).
        Figura 9.7.99

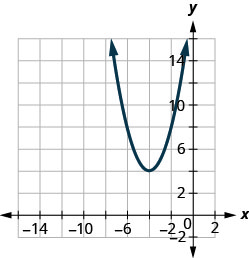
      4. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 4, 4) y otros puntos (negativo 6, 8) y (negativo 2, 8).
        Figura 9.7.100

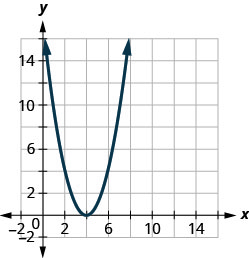
      5. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (4, 0) y otros puntos (2, 4) y (2, 4).
        Figura 9.7.101

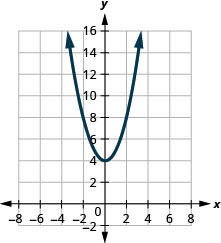
      6. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (0, 4) y otros puntos (negativos 2, 8) y (2, 8).
        Figura 9.7.102

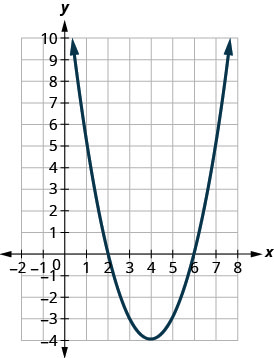
      7. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (4, negativo 4) y otros puntos (2,0) y (6,0).
        Figura 9.7.103

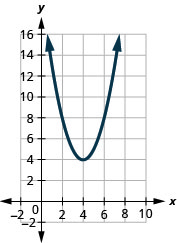
      8. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (4, 4) y otros puntos (2,8) y (6,8).
        Figura 9.7.104
    Contestar

    1. c

    3. e

    5. d

    7. g

    Ejercicio\(\PageIndex{33}\) Find a Quadratic Function from its Graph

    En los siguientes ejercicios, escribe la función cuadrática en\(f(x)=a(x−h)^{2}+k\) forma cuya gráfica se muestra.


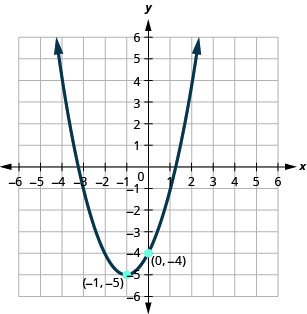
    1. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 1, negativo 5) e intercepción y (0, negativo 4).
      Figura 9.7.105

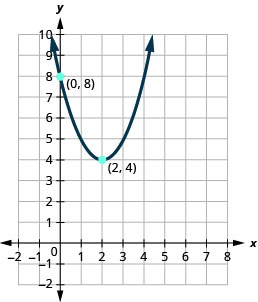
    2. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (2,4) e intercepción y (0, 8).
      Figura 9.7.106

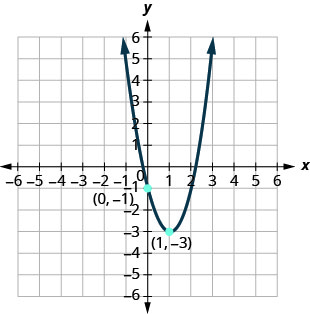
    3. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (1, negativo 3) e intercepción y (0, negativo 1).
      Figura 9.7.107

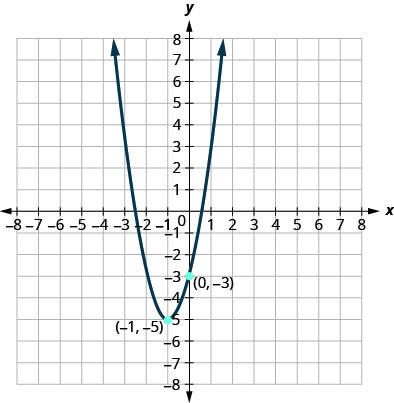
    4. Esta figura muestra una parábola de apertura hacia arriba en el plano de la coordenada x y. Tiene un vértice de (negativo 1, negativo 5) e intercepción y (0, negativo 3).
      Figura 9.7.108
    Contestar

    1. \(f(x)=(x+1)^{2}-5\)

    3. \(f(x)=2(x-1)^{2}-3\)

    Ejercicio\(\PageIndex{34}\) Writing Exercise
    1. Grafica la función cuadrática\(f(x)=x^{2}+4x+5\) primero usando las propiedades como hicimos en la última sección y luego graficarla usando transformaciones. ¿Qué método prefieres? ¿Por qué?
    2. Grafica la función cuadrática\(f(x)=2x^{2}−4x−3\) primero usando las propiedades como hicimos en la última sección y luego graficarla usando transformaciones. ¿Qué método prefieres? ¿Por qué?
    Contestar

    1. Las respuestas pueden variar.

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

    Esta figura es una lista para evaluar tu comprensión de los conceptos presentados en esta sección. Tiene 4 columnas etiquetadas I can…, Confianza, Con alguna ayuda, y No-I don’ t get it! Debajo de I can…, hay gráfico Funciones Cuadráticas de la forma f de x es igual a x cuadrado más k; gráfico Funciones cuadráticas de la forma f de x es igual a la cantidad x menos h cuadrado; graficar Funciones cuadráticas de la forma f de x es igual a veces x cuadrado; graficar Funciones cuadráticas Usando Transformaciones; encontrar a Función Cuadrática a partir de su Gráfica. Las otras columnas se dejan en blanco para que compruebes tu comprensión.
    Figura 9.7.109

    b. después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?

    This page titled 9.8E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.